Многомасштабное моделирование процессов и структур в нанотехнологиях
Подождите немного. Документ загружается.


91
няется постоянной угловая ориентация гексагональной решетки графена
по отношению к осям симметрии поверхности металла.
Работа выполнена в рамках грантов РФФИ 08-03-00410, 08-08-00752 и
поддержана ФЦП, контракты 02.518.11.7029 и 02.513.11.3355.
Список литературы
1. Dobrotvorskii A.M., Afanasjeva O.V. A quasifermion approach to modelling interatomic
interactions in solids // J. Phys.: Condens. Matter. – 1993. - Vol.5, N 47. — p.8839-8848.
2. Адамчук В.К., Вяткин А.Г., Добротворский A.M., Шикин A.M., Широков Д.В. Иссле-
дование относительной устойчивости твердых фаз в системе La-графит методом многоцен-
трового атом-атомного потенциала. // ФТТ — 1997. — Т.39, вып.10 — с.1870-1882.
3. Добротворский А.М., Адамчук В.К. Моделирование атомных механизмов релаксации
локальных деформаций на поверхности
золота. // ЖТФ — 1994. — Т.64, вып.8 — с. 132-144.
4. Усачев Д.Ю., Добротворский А.М., Варыхалов А.Ю., Rader O., Gudat W., Шикин
А.М., Адамчук В.К. Экспериментальное и теоретическое исследование морфологии графена
на соразмерных и несоразмерных поверхностях монокристалла Ni. // ФТТ — 2008. В печати.
Б.Н. ГРУДИН, С.В. ДОЛЖИКОВ
, В.С. ПЛОТНИКОВ,
Е.С. СЛАБЖЕННИКОВ
Дальневосточный государственный университет
МОДЕЛИРОВАНИЕ СТРУКТУР
НАНОКРИСТАЛЛИЧЕСКИХ И АМОФНЫХ СПЛАВОВ
Рассматриваются и демонстрируются возможности моделирования структуры
аморфных и нанокристаллических материалов с использованием моделей случай-
ной плотной упаковки. Для построения изображений атомной структуры реализо-
ваны расчеты различных моделей и их модификаций.
Для построения модели принимались во внимание два типа моделей
металлов: случайные плотноупакованные (СПУ) ансамбли и модели кла-
стеров, в которых структурный элемент определяется при помощи хими-
ческой интуиции или из аналогии с кристаллическими структурами.
Можно исходить из вида потенциала для решения структурной проблемы
в случайном ансамбле атомов. Однако такой метод только
частично под-
ходит даже для одноатомных сплавов (т.к. получившиеся структуры очень
чувствительны к виду потенциала). При выборе типа модели было решено
остановиться на СПУ - типе, как наиболее полно поддающемся програм-
мированию на ЭВМ. Применяющиеся в таком типе алгоритмы составляют
кластер укладкой атомов по одному, что соответствует физической карти-
не
конденсации вещества. Кластеры, рассчитанные таким образом, можно
использовать как элементы при создании модели из некристаллических
92
кластеров. Такие модели отличаются возможностью создания особо
больших моделей, которые имеют уже макроскопические размеры, в них
можно рассматривать структуры, находящиеся на стыке микро- и макро-,
что довольно интересно для исследователя. Изучением структуры аморф-
ных металлов, построением их моделей и реализацией их на ЭВМ зани-
мались такие ученые как: К. Судзуки, Х
. Фудзимори, К. Хасимото, Иши-
кава, Такаяма, Ч.Беннет, Финней, Гольдшмит, Садок, Бакай, Воронов,
Фельц, Полухин , Белащенко, Манохин. Решено было программно реали-
зовать расчеты моделей Беннета, Финнея и Ишикавы [1-5].
По результатам моделирования установлено, что ФРР, рассчитанные
для моделей, и экспериментальные ФРР имеют общие закономерности,
например, наблюдается раздвоение второго пика. Выявлено, что
модель
Беннета приводит к достаточно неоднородной структуре, что проявляется
на модельных изображениях. Обычно в центре кластера коэффициент
упаковки составляет 0.64 - 0.67, а с увеличением размера моделируемой
структуры до 4-5 тысяч твердых сфер, он падает до 0.62. Левый пик вто-
рого раздвоенного максимума у аморфных металлов обычно выше право-
го, в модели же Беннета соотношение обратное
.
Выбор остановился на модели Ишикавы, которая обеспечивает доста-
точно хорошее соответствие с экспериментальными данными. Были про-
ведены модификации, чтобы сделать ее более универсальной. Хорошие
результаты получены с использованием модели Ишикавы, для которой
нами введено минимальное расстояние между атомами. В этом случае
модернизированная таким образом модель дает хорошо совпадающую с
экспериментальной
форму ФРР.
Расчет плотности упаковки позволяет сравнить плотность этой модели
с плотностью реальных материалов или других моделей. В целом, можно
сказать, картина, создаваемая моделью, соответствует реальному положе-
нию вещей. Форма ФРР, рассчитанная из модели и экспериментальные
графики имеют общие закономерности.
Модернизированная модель при увеличении минимального расстояния
между атомами приводит к растяжению
всей ФРР вправо и падению
плотности кластера. Тем не менее, отношения r
2
/r
1
и r
3
/r
1
, где r
i
– радиус i
– ой координационной сферы, оказываются равными соответственно 1.73
и 1.94. Эти значения близки к экспериментальным данным для структуры
аморфных сплавов на основе железа (1.69 и 1.98).
При помощи программы на основе модифицированного алгоритма
Ишикавы, Бенета, Феннея построены модели кластеров с различным ко-
личеством атомов, по которым рассчитаны функции радиального распре-
деления. Проведено сравнение модельных
функций радиального распре-
деления с экспериментальными, выявлено согласие модельных и экспе-
риментальных функций радиального распределения.

93
Работа выполнена в рамках инновационной образовательной програм-
мы ДВГУ приоритетного национального проекта «Образование».
Список литературы
1. Судзуки К., Фудзимори Х., Хасимото К. Аморфные металлы, М.: Металлургия, 1987.
2. Александров Л.Н. Моделирование роста и легирования полупроводниковых пленок
методом Монте-Карло. Н.: Наука, 1991.
3. Белащенко Д.К., Канонические структуры однокомпонентных аморфных тел // ФММ,
1987. Вып. 4. С. 665 - 671.
4. Finney J.L., Gellatlv B.J., Wallace J. Metallic glasses: Science and Technology. - Budap-
est. - 1980. - 1 - 55.
5. Бакай А.С. Поликластерные аморфные тела
. М.: Наука, 1988.
С.В. ДОЛОТОВ
, В.И. РОЛДУГИН
Институт физической химии и электрохимии им. А.Н. Фрумкина РАН
МОДЕЛИРОВАНИЕ СПЕКТРОВ ЭПР В АГРЕГАТАХ
МЕТАЛЛИЧЕСКИХ НАНОЧАСТИЦ
По специальному алгоритму построены агрегаты из моно- и полидисперсных
частиц, характеризующиеся наперёд заданными величинами фрактальной размер-
ности и префактора. В приближении самосогласованного поля проведён расчёт
спектров ЭПР таких агрегатов. Показана зависимость спектра ЭПР агрегата от его
размера, фрактальной размерности, характера упаковки крупных и мелких частиц
для агрегата, состоящего из полидисперсных наночастиц
.
Исследование электронных свойств наночастиц представляет большой
научный и практический интерес. Он объясняется и необычным поведе-
нием электронной подсистемы при переходе к нанометровым размерам
частиц, и возможными применениями наночастиц в электронных устрой-
ствах различного назначения. Одним из основных методов изучения элек-
тронных подсистем является метод ЭПР.
Наночастицы, диспергированные в жидких средах, как
правило, агре-
гируют, что естественным образом сказывается на спектрах ЭПР. В дан-
ной работе исследованы закономерности изменения спектров ЭПР фра-
тальных агрегатов монодисперсных и полидисперсных металлических
наночастиц. Изучено также влияние на спектр ориентации магнитного
поля относительно анизотропных агрегатов.
При расчёте спектров ЭПР учитывалось только наиболее существен-
ное диполь-дипольное взаимодействие
спинов электронов, принадлежа-
щим разным частицам. В результате были получены алгоритмы для рас-
94
чёта спектров электронного парамагнитного резонанса агрегатов поли-
дисперсных наночастиц и спектров ЭПР цепочек наночастиц при различ-
ной ориентации магнитного поля. Расчет магнитной восприимчивости
осуществлялся для параметров, определённых в экспериментах для нано-
частиц натрия.
В результате проведения расчётов было выявлено, что на спектры ЭПР
агрегатов монодисперсных частиц влияют размер агрегата и величина
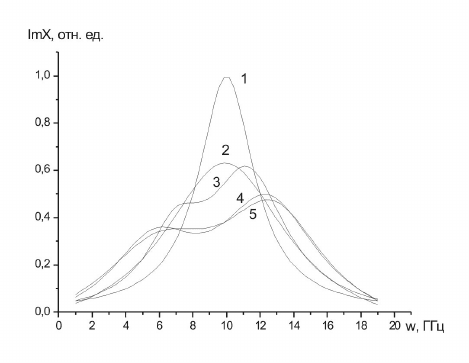
фрактальной размерности. Например, на рис. 1 показано изменение спек-
тра ЭПР агрегата с ростом его размера. Интересно отметить, что сначала
происходит уширение полосы, а расщепление её на несколько полос на-
чинается для достаточно крупных агрегатов. Дальнейший рост размера
агрегата приводит к естественному уширению полос. При этом важно
отметить, что это уширение
идёт достаточно слабо при изменении числа
частиц в агрегате от 35 до 100. Эти полосы связаны с особенностями
фрактальной структуры агрегатов: в таких агрегатах имеются статистиче-
ски доминирующие значения расстояний между частицами, обусловлен-
ные самоподобием структурной организации агрегатов. Этим расстояни-
ям соответствует усиление спектра поглощения в определенном диапазо-
не частот, что и наблюдается
на всех определённых нами спектрах ЭПР.
Видно, что расщепление на полосы идёт после того, как произойдёт “на-
копление” статистически доминирующих расстояний между частицами.
Рис. 1. Характер изменения спектра ЭПР агрегата монодисперсных наночастиц с
фрактальной размерностью
9.1=
f
d с ростом его размера: 1 – одиночная части-
ца; 2, 3, 4, 5 – агрегаты, содержащие 7, 10, 37 и 100 частиц соответственно
95
Анализ расчетных спектров агрегатов полидисперсных наночастиц по-
казал, что при малой ширине распределения частиц агрегата по размерам
в спектре ЭПР наблюдается две полосы, а при достаточно большой – од-
на. Расщепление спектра на полосы, как говорилось выше, обусловлено
наличием в агрегате статистически доминирующих значений расстояний
между частицами, где взаимодействие достаточно сильно, чтобы
проявить
себя в спектре. С ростом ширины распределения появляется всё большее
число частиц разных размеров, что приводит к случайному изменению
расстояний между ними и, как следствие, к изменению положения резо-
нансных полос между ними. В результате множество полос сливаются в
одну полосу. Выявлена также зависимость спектров ЭПР полидисперсных
систем от
порядка расположения крупных и мелких частиц в агрегате.
А.П. ДУДКА
Институт кристаллографии им. А.В. Шубникова РАН
ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ ЭЛЕКТРОННОЙ
ПЛОТНОСТИ В КРИСТАЛЛАХ РАСШИРЕННОЙ
МУЛЬТИПОЛЬНОЙ МОДЕЛЬЮ
Проблема корреляции кристаллической структуры и физических
свойств может быть решена с помощью анализа электронной плотности.
Обычно электронная плотность представляется в виде разложения по
сферическим гармоническим функциям. Но в существующих программах
используется разложение только до четвертого порядка.
В пакете программ ASTRA электронная плотность описана мульти-
польной моделью до восьмого порядка. Расчеты возможны как
для клас-
сического случая дифракции рентгеновских лучей, так и для новых пер-
спективных методов. Уточняемыми параметрами мультипольной модели
являются каппа-параметры, которые описывают расширение/сжатие элек-
тронных оболочек и коэффициенты заселенности валентных и деформа-
ционных оболочек. В ASTRA возможно оптимизировать до 12 каппа-
параметров и до 84 коэффициентов заселенности для одного атома.
Показано,
что мультипольная модель выше четвертого порядка явля-
ется весьма значимой для многих неорганических кристаллов. В качестве
тестового образца в работе использован кристалл кремния. Точно изме-
ренные интегральные интенсивности для кремния обеспечивают превос-
ходную проверку структурных уточнений. Консолидированный набор
данных состоял из 31 рефлекса, включая рефлекс 222, запрещенный пра-
вилами погасаний по симметрии [1]. Измеренный
структурный фактор
96
для рефлекса 222 равен Fobs = 0.728. Единственным уточняемым пара-
метром для модели независимых атомов является тепловой параметр B.
Мультипольная модель состоит из 5 параметров (до четвертого порядка -
MP4) или из 8 параметров (до восьмого порядка - MP8). Данные измерены
в абсолютной шкале, поэтому шкальный фактор Kscale должен быть ра-
вен 1.
Показано, что мультипольная модель выше четвертого порядка явля-
ется весьма
значимой для многих неорганических кристаллов. В качестве
тестового образца в работе использован кристалл кремния. Точно изме-
ренные интегральные интенсивности для кремния обеспечивают превос-
ходную проверку структурных уточнений. Консолидированный набор
данных состоял из 31 рефлекса, включая рефлекс 222, запрещенный пра-
вилами погасаний по симметрии [1]. Измеренный структурный фактор
для рефлекса 222 равен Fobs = 0.728. Единственным уточняемым пара-
метром
для модели независимых атомов является тепловой параметр B.
Мультипольная модель состоит из 5 параметров (до четвертого порядка -
MP4) или из 8 параметров (до восьмого порядка - MP8). Данные измерены
в абсолютной шкале, поэтому шкальный фактор Kscale должен быть ра-
вен 1.
Показано, что мультипольная модель до восьмого порядка является
предпочтительной, так как (1) дает намного лучшую подгонку, чем MP4
(0.221
→ 0.072%); (2) она лучше объясняет измеренный структурный фак-
тор для рефлекса 222 (0.853
→ 0.724); (3) уточнение шкального фактора
дает Kscale = 0.9993(5) вместо 0.9957(5) для MP4; (4) параметры для MP8
больше, чем 2 s.u.; (5) уточнение шкального фактора оказывает меньшее
влияние на подгонку.
В ASTRA возможно уточнение мультипольной модели для дифракции
рентгеновских лучей на монокристаллах, для дифракции электронов на
поликристаллах и для прецессионной электронной дифракции с учетом
многоволнового взаимодействия с использованием метода Блоховских
волн [2].
Список литературы
1. Zuo J. M., Blaha P. and. Schwarz K // J. Phys. Condens. Matter. 9 (1997) 7541.
2. Dudka A..P. Modeling of experimental electron density by multipole model up to eighth
order//International conference "Electron Microscopy and Multiscale Modeling-2007
EMMM'2007", Moscow, 3-7 September 2007. Book of abstracts. P.31.
97
С.З. ДУНИН, О.В. НАГОРНОВ
Московский инженерно-физический институт (государственный университет)
МОДЕЛИРОВАНИЕ ПАРАМЕТРОВ ВЫСЫХАЮЩЕЙ
КАПЛИ, РАСПОЛОЖЕННОЙ НА ПОЛНОСТЬЮ
СМАЧИВАЕМОЙ ПОВЕРХНОСТИ
В работе проведено вычисление параметров капли жидкости на полностью
смачиваемой горизонтальной подложке в процессе её испарения.
Последнее время интенсивно исследуются возможности самооргани-
зации органических и неорганических веществ, растворенных в малых
объемах жидкости. Например, закономерности в архитектуре растворен-
ных в каплях крови веществ после высыхания жидкости, позволяют су-
дить о характере заболевания [1]. В работе [2] предложено растворять в
капле жидкости анизотропные наночастицы, которые по мере высыхания
капли образуют упорядоченные
структуры, используемые при создании
наноструктурных материалов и устройств для контроля летучих веществ.
Испаряющаяся капля представляет собой открытую термосистему, из
которой растворенные в ней наночастицы не могут выйти благодаря по-
верхностному натяжению, вынуждающему наночастицы сближаться по
мере высыхания капли. Сложные гидродинамические процессы, проте-
кающие в капле по мере её высыхания во
многом обеспечивают архитек-
туру наночастиц.
В работе изучается гидродинамический режим испарения капли из со-
стояния полного смачивания. Параметры такой капли жидкости указаны в
[3]. Капля представляет собой шаровой сегмент высоты
(
)
L
RtH , – ради-
ус сегмента – подвижная граница трехфазной линии твердое тело, жид-
кость и газ, перемещающаяся к центру по мере испарения капли. На рас-
стоянии
r
от оси симметрии капли ее сферическая поверхность опреде-
ляется формулой
()
()
()
()
()
()
2
22 22
2
0, 0,
1
,
20, 20, 2
LL
L
htR htR
hrt r R t
ht ht
θ
⎛⎞
+−
=−+≈⋅
⎜⎟
⎜⎟
⎝⎠
,
где
θ – краевой угол, остающейся постоянным в процессе испарения кап-
ли. После интегрирования уравнения непрерывности
() ()
2
1,
1
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+−=ρ
∂
∂
ρ+
∂
∂
ρ
r
h
trJvh
rrt
h
S
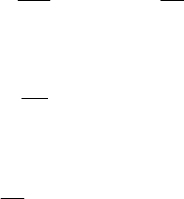
98
для скорости получаем
,),(
1
),(
0
∫
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
ρ
=
r
s
drr
t
h
trJ
hr
trv
(1)
где
S
J – масса воды, испаряющаяся с единицы поверхности в единицу
времени. Мы считаем, что
1<<θ≈
∂
∂
r
h
. Временная зависимость радиуса
капли определяется уравнением (1) при
(
)
tRr
L
= :
()
()
2/1
0
/,0),( rtRCJdrr
t
h
trJ
LS
R
s
L
−==
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
∫
.
Знание
()
tR
L
позволяет определить параметры высыхающей капли. В
последующих расчетах эти параметры войдут как входные данные, опре-
деляющие динамику наноанизотропных частиц в капле. Самосборка на-
ночастиц дает возможность получать особо прочные соединения [4].
Работа поддержана госконтрактом № 02.513.11.3363.
Список литературы
1.
ТарасевичЮ.Ю. 2004. Механизмы модели дегидратационной самоорганизации био-
логических жидкостей,УФН. Том 174, сс. 779-790.
2.
Алфимов М.А. и др. 2004. Имитационное моделирование процессов самоорганиза-
ции наночастиц Российские нанотехнологии. Том 1-2, сс. 127-132.
3.
De Gennes P.G. 1985. Wetting: Statics and Dynamics. Rev. Mod. Rhys, V.57, pp . 827-
863.
4.
Фейнман Р. 2002. Внизу полным-полно места: приглашение в новый мир физики.
Российский химический журнал. Том 46, №5, сс.4-6.
А.Б. ДЮБУА
Рязанский институт открытого образования
МОДЕЛЬ ПЛАЗМЕННЫХ ОСЦИЛЛЯЦИЙ В 2D
ЭЛЕКТРОННОЙ СИСТЕМЕ С ТОНКОЙ СТРУКТУРОЙ
ЭНЕРГЕТИЧЕСКОГО СПЕКТРА
В настоящей работе сообщаются результаты исследований электрон – элек-
тронных релаксационных процессов в системе сильновырожденных 2D электро-
нов с тонкой структурой энергетического спектра и пространственного распреде-
ления электронной плотности. Показано, что осцилляции температурной и кон-
центрационной зависимости времени электрон – электронного взаимодействия

99
связаны с возбуждением плазменных колебаний компонентов 2D электронной
системы.
Работа направлена на выяснение вклада внутриподзонной
intra
ee
τ
и меж-
подзонной
inter
ee
τ
электрон – электронной релаксации в затухание кванто-
вания Ландау осцилляций поперечного магнитосопротивления. Для силь-
нолегированного (
11 -2
8.5 10 ńě
s
n >⋅ ) гетероперехода
1
()/
xx
A
lGa AsSi GaAs
−
,
аппроксимированного треугольным потенциальным профилем, когда за-
полнены основная и возбужденная подзоны размерного квантования, по-
лучены выражения параметрических зависимостей
intra
ee
τ и
inter
ee
τ от тем-
пературы
T , которые объясняют экспериментальные зависимости [1].
Методом самосогласованного решения уравнений Пуассона и Шрединге-
ра, были найдены вид энергетической структуры для зоны проводимости
()
c
E
z наноструктуры и пространственное распределение электронной
плотности
() ()
*
z
zψψ на уровнях (подзонах) размерного квантования [2].
С точностью до второго члена разложения внешнего возмущающего по-
тенциала теории возмущений выражение для времени “е-е” взаимодейст-
вия может быть представлено в виде
()()
(
() ()
)
()()
2
,,
1
(, )
11,
ijkl
tot j l i k
ee
km
ij
dV E E EE
ff f f
∞
−∞
+
=ω ω δ ++ − − ×
τ
×− −
∑∑ ∑
∫
qkp
kp kq p-q
qkqp-qkp
где
()
,
ijkl
tot
V ωq — матричный элемент полного потенциала экранирования,
f — функция распределения Ферми — Дирака [3].
Традиционный подход к решению подобных задач состоит в рассмот-
рении условий абсолютного нуля (0T
=
К), ограничением разложения
матричных элементов до членов второго порядка малости [4], что связано
с логарифмической расходимостью членов высшего порядка разложения.
Решение поставленной задачи требует иного подхода,— а именно: усло-
вие 0T ≠ К. Интегрирование связано с некоторыми особенностями: при
небольших температурах происходит переход к так называемому «гидро-
динамическому режиму», который можно описать
с помощью макроско-
пических законов гидродинамики и термодинамики. Макроскопические
ситуации принципиально отличаются от предела 0T
≡
. В этом пределе
частота столкновений обратится в ноль, а диэлектрическая функция
(, )χω
q , входящая в
()
,
ijkl
tot
V
ω
q будет соответствовать бесстолкновитель-

100
ному режиму [5]. Функция
(
)
,
tot
V
ω
q имеет в комплексной плоскости
частот особую точку, поэтому следует вначале проводить суммирование
по волновым векторам
, kp
и q , а уже затем интегрирование по частоте
ω . Необходимо также отметить, что в большинстве работ по исследова-
нию ”е-е” взаимодействий используется статический предел так, что
(, ) (,0)
χω≡χqq. В нашей задаче функция распределения имеет достаточ-
но сложную структуру. И поэтому возможно ожидать резонансные откли-
ки на непрерывный спектр потенциала внешнего возмущения. Следова-
тельно, решение поставленной задачи требует исследования частотной
зависимости
(
)
,
tot
V
ω
q с использованием приближения хаотических фаз,
суть которого состоит в пренебрежении связью между изменениями Фу-
рье – образов плотностей, относящихся к разным длинам волн.
Список литературы
1.
Kadushkin V.I., Dubois A.B. Intra- and Intersubband Interaction as a Factor Contributing to
the Damping of Landau Quantization in Two-Dimensional Electron Gas, Physics of Low-Dim. Str.
№9/10. – p.11-24, (2003).
2.
Kadushkin V.I., Dubois A.B. “Bottleneck” in Electron – Electron Interactions and Anoma-
lies in the Landau Quantization Damping Phys. Low-Dim. Struct., 7/8, 7-24 (2003).
3.
Kadushkin V.I., Dubois A.B. The Role of Electron – Electron Relaxation in Landau Quan-
tization Damping Phys. Low-Dim. Struct., 11/12, 27-37 (2002).
4.
Slutzky M., Entin-Wohlman O., Berk Y., and Palevsky A. Electron-electron scattering in
coupled quantum wells // Phys. Rev. B, №53(7), p. 4065-4072, (1996)
5.
Пайнс Д., Нозьер Ф. Теория квантовых жидкостей. М.: Наука. (1967).
Е.А. ЕЛФИМОВА, А.О. ИВАНОВ, Е.В. КРУТИКОВА
Уральский государственный университет им. А.М.Горького, Екатеринбург
МЕЖЧАСТИЧНЫЕ КОРРЕЛЯЦИИ
В ИОННОСТАБИЛИЗИРОВАННЫХ
МАГНИТНЫХ НАНОКОЛЛОИДАХ
На базе термодинамической теории возмущений развита модель, описываю-
щая межчастичные корреляции в ионностабилизированных коллоидных диспер-
сиях магнитных наночастиц как в присутствии, так и в отсутствии внешнего маг-
нитного поля. Определены парная корреляционная функция и структурный фак-
тор рассеяния исследуемой системы. Получено хорошее согласование теоретиче-
ских результатов и данных компьютерного моделирования.
Устойчивые коллоидные дисперсии магнитных наночастиц в жидких
носителях называют магнитными жидкостями или феррожидкостями. Бы-
