Миронов С.В., Пищухин А.М. Метасистемный подход в управлении

211

()()

(

)

(

)

(

)

∑

∈

−

=

∈

Xx

xfxfxHXxxfH

2

log| . (В.37)

Обычно функцию (В.37) называют шенноновской энтропией. Она изме-

ряет нечеткость в единицах, называемых битами.

Рассмотрим теперь порождающую нечеткость в системах, описываемых

с помощью функций распределения возможностей. Пусть П – это множество

всех распределений возможностей, имеющих по крайней мере одно ненуле-

вое значение, которые можно определить на конечных множествах альтерна-

тивных исходов. Тогда возможностная мера нечеткости представляет собой

функцию

[

]

∞

→ ,0: ПU , (В.48)

обладающую определенными свойствами. Прежде чем рассматривать эти

свойства, нужно сначала ввести некоторые понятия, связанные с распределе-

ниями возможностей.

1 Распределение возможностей

(

)

ПNif

X

∈

=

||

|

ϕ

, (В.51)

определенное на конечном множестве X альтернативных исходов x на-

зывается нормализованным распределением возможностей тогда и только

тогда, когда

1max

=

i

ϕ

; (В.52)

понятно, что )(xf

i

=

ϕ

для некоторого взаимнооднозначного соответствия

между N

|X|

и X.

2 Пусть для любого распределения возможностей f, например для рас-

пределения, определенного в (49), и для любого действительного

[]

1,0∈l

[

]

(

)

NPПc →

×

1,0: (В.53)

такая функция, что

(

)

}|{, lNilfc

i

X

≥

∈

=

ϕ

. (В.54)

Эта функция называется функцией l-уровня, а множество

()

lfc ,- множеством

l- уровня от f.

3 Для заданного распределения возможностей (49) назовем

(В.55)

уровневым множеством для f. Обозначим через

},...,,{

21 qf

lllL

=

уровневое множество для f, где l

1

=0,

f

Lq = , причем из ji < следует, что

ji

ll < . Пусть для удобства

i

f

l

ϕ

max

=

.

Понятно, что

fqf

Lll ∈= . Кроме того, 1

=

f

l тогда и только тогда, когда f яв-

ляется нормализованным распределением возможностей.

4 Для любого

N

m∈ пусть

(

)

}0)(|{

=

∈

= lилиlNEilL

i

X

f

ϕ

212

(

)

ПNif

mi

∈∈= |

11

ϕ

,

(

)

ПNif

mi

∈∈= |

22

ϕ

,

два распределения возможностей. Тогда f

1

называется субраспределением

f

2

тогда и только тогда, когда для любого

m

Ni

∈

i

ϕϕ

21

maxmax = и

ii

ϕϕ

21

≤ .

Пусть

ff

21

≤ означает, что f

1

является субраспределением f

2

. Понятно, что

отношение «

f

1

субраспределение f

2

» представляет собой частичное упоря-

дочение, определенное на любом множестве распределений возможностей с

числом элементов, равным m. Обозначим это множество

П

m

. Далее (

П

m

,

≤

)

– это решетка с объединением и пересечением, определяемыми соответст-

венно как

f

1

∨ f

2

[

]

(

)

mii

Ni ∈= |,max

21

ϕϕ

,

f

1

∨ f

2

[

]

(

)

mii

Ni ∈= |,min

21

ϕϕ

для любых

f

1

, f

2

П

m

∈

.

Теперь, располагая определенными понятиями, связанными с рапсреде-

лениями возможностей, можно вернуться к обсуждению главного вопроса – о

мере возможностной нечеткости. Хотелось бы, чтобы возможностные анало-

ги свойств Н1 – Н5, которыми обладает шенноновская энтропия, также вы-

полнялись бы и для возможностной меры нечеткости. Возможностные анало-

ги этих свойств можно сформулировать точно так же, как Н1-Н5, за тем

только исключением, что слово «вероятность» нужно везде изменить на сло-

во «возможность». Функция вида (48), удовлетворяющая этим свойствам, из-

вестна. Ее можно представить в виде

() ()

∑

−

=

++

−=

1

11

,log)(

1

q

k

kkk

f

lfcll

l

fU

, (В.56)

или в более простом виде

() ()

∫

=

f

l

f

dllfc

l

fU

0

2

,log

1

. (В.57)

Эта функция называется

U – нечеткостью. Помимо возможностных

аналогов свойств Н1-Н2,

U – нечеткость обладает некоторыми другими по-

лезными свойствами. Важнейшим из них является

монотонность: для лю-

бых

()

NmПff

m

∈∈

21

,, если ff

21

≤ , то

(

)

(

)

fUfU

21

≤ .

В.6 Поиск подходящих систем с поведением

Располагая теперь мерами нечеткости, через которые выражается сте-

пень детерминированности, вернемся в данном разделе к типу задач, введен-

ному в разделе 6.4; дана система данных

D с полностью упорядоченным па-

раметрическим множеством и с наибольшей допустимой маской

М, совмес-

213

тимой с D; требуется определить все системы с поведением, удовлетворяю-

щие требованиям согласованности, детерминированности и простоты, при-

чем требование согласованности более приоритетно, чем остальные два.

Любая наибольшая допустимая маска

М содержит набор корректных

масок, каждая из которых является подмножеством

М. Для каждой маски

может быть определена функция поведения (определенного выбранного ти-

па), хорошо согласующаяся с данными, с помощью разреженной выборки

данных. Однако на практике достаточно провести выборку только для маски

М. Функции поведения для ее подмасок могут быть получены вычислением

подходящих проекций функции поведения соответствующей маске

М.

Для заданной функции f

B

, определенной через полные состояния неких

выборочных переменных, любая из ее проекций также является функцией

поведения, соответствующей f

B

в смысле субсостояний, основанных на опре-

деленном подмножестве выборочных переменных. Пусть

)(

M

k

Nks ∈

- выбо-

рочные переменные, через которые определяются состояния f

B

; М – маска,

через которую выбираются значения выборочных переменных. Пусть

[

]

Zf

B

↓ - проекция f

B

, где подмножество множества N

|M|

идентификаторов

выборочных переменных, то есть

N

Z

⊂ . Тогда

[

]

1,0:][ →×↓

∈

k

Zk

B

SZf , (В.67)

так что

[

]

(

)

(

)

})|({ xccfaxZf

B

f=↓ , (В.68)

где

а – некая агрегирующая функция, определяемая характером функции f

B

.

Например,

[

]

(

)

(

)

∑

=↓

xc

BB

cfxZf

f

, (В.69)

где f

B

– распределение вероятностей; соответственно для распределения воз-

можностей,

[

]

(

)

(

)

xc

BB

cfxZf

f

max=↓ . (В.70)

Будем в контексте любой конкретной задачи через

B

f

1

обозначать функ-

цию поведения для наибольшей приемлемой маски

М. Через

()

,...3,2=if

B

i

,

будем обозначать функции поведениядля ее различных осмысленных подма-

сок

M

i

, каждая из которых связана с множеством

M

i

NZ ⊂ идентификато-

ров выборочныз переменных.

За исключением очень небольших наборов данных, с точки зрения вы-

числений проще определять функции поведения с помощью проекций, а не

через выборки данных. Чем больше объем данных, тем больше вычислитель-

ного времени экономится. Таким образом, лучше производить выборку толь-

ко однажды для наибольшей приемлемой маски, а затем определять функции

поведения для всех содержательных подмасок как соответствующие проек-

ции.

Пример В.4 Определим проекцию вероятностной функции поведения,

214

приведенной в таблице В.1 и возможностной функции поведения, приведен-

ной в таблице В.2 для Z ={1,2}.

Таблица В.1

S

1

S

2

S

3

S

4

f(c)

0 0 0 0 0.2

0 0 0 1 0.2

0 0 1 0 0.1

0 1 0 1 0.1

1 0 0 0 0.1

1 0 1 0 0.1

1 1 0 1 0.1

С=

1 1 1 0 0.1

Таблица В.2

S

1

S

2

S

3

f(c)

0 0 0 1.0

0 0 1 0.25

0 1 1 0.25

1 0 0 0.5

С=

1 1 1 0.5

Применив формулу (В.58) для вероятностной функции, получим:

S

1

S

2

[f↓{1,2}](x)

0 0 0.5(=0.2+0.2+1)

0 1 0.1

1 0 0.2(=0.1+0.1)

x=

1 1 0.2(=0/1+0/1)

Для возможностной функции по формуле (В.59) имеем

S

1

S

2

[f↓{1,2}](x)

0 0 1.0

0 1 0.25

1 0 0.5

x=

1 1 0.5

Для заданной системы данных

D и наибольшей допустимой маски М

требование соответствия приводит к ограниченному множеству

(

)

)},(,...,2,1|,,{ MnNifMIFY

ii

B

i

r

∆=== ,

содержащему по одной системе с поведением для каждой осмысленной мас-

ки

MM

i

⊆ ; пусть для удобства

M

=

1

. Следующим шагом решения рас-

215

сматриваемой задачи должно быть вычисление степеней недетерминирован-

ности и сложности для всех систем из множества

r

Y .

Как было показано в разделе В.5,

степень недетерминированности за-

дается соответствующей мерой

порождающей нечеткости, определяемой

для вероятностных систем шенноновской энтропией, а для возможностных

систем

U – нечеткостью. Для определения порождающей нечеткости требу-

ется, чтобы был определен порядок порождения (и соответствующее разбие-

ние любой маски). Если допускается несколько порядков порождения, то для

каждой маски мы берем порядок с наименьшей порождающей нечеткостью.

Что касается

меры сложности, то тут возможно много вариантов.

Возьмем для примера простую, но содержательную меру – размер (мощ-

ность) маски. Пусть ,...)2,1(

=iq

u

i

- значение соответствующих порождающих

нечеткостей для систем с поведением

B

i

F из ограниченного множества Y

r

.

Поскольку любая система F

B

однозначно идентифицируется своей маской М,

мощность которой

M

i

задает ее сложность, статус системы

B

i

F в смысле

порождающей нечеткости и сложности удобно описывать парой

(

)

u

ii

qM ,.

Теперь рассматриваемую задачу можно обсуждать в терминах масок

M

i

, а

не соответствующих систем с поведением

B

i

F .

Численное упорядочение масок

M

i

, идентифицирующих системы из Y

r

по их мощности, задает

упорядочение сложности

с

≤

на множестве Y

r

. Чис-

ленное упорядочение значений

u

i

q определяет упорядочение по нечеткости

u

≤ на множестве Y

r

. В то время, как упорядочение по сложности полностью

определяется самими масками, упорядочение по нечеткости может быть оп-

ределено только после оценки масок. Для любого множества порождающих

масок мы можем определить частичное упорядочение

G

j

G

i

MM ≤ тогда и

только тогда, когда

ggиgg

iiii

<= . (В.60)

(или

ee

ii

< для направленных систем), которое мы будем называть упо-

рядочением подмасок.

Это упорядочение часто оказывается полезным при

разработке различных эвристических процедур поиска на множестве систем

Y

r

.

Пример упорядоченности по сложности и упорядоченности подмасок

для наибольшей допустимой маски М при n=3 u ∆M=2 приведен далее... Из

этого примера видно, что упорядочение по сложности – это связное квазиу-

порядочение (рефлексивное и транзитивное отношение, определенное для

любой пары систем).

Упорядочение по подмаскам – это частичное упорядочение, но решетки

оно не образует. Однако оно представляет собой набор решеток по одной для

каждого множества порождаемых выборочных переменных (в нашем приме-

216

ре это крайние правые элементы масок).

Упорядочение по нечеткости связное, но из-за того, что несколько раз-

ных систем могут иметь одинаковую порождающую нечеткость, это отноше-

ние не является антисимметричным. Следовательно, в общем случае это

связное квазиупорядочение, которое в некоторых частных случаях оказыва-

ется полным упорядочением.

Таким образом, на множестве Y

r

определены два связных квазиупорядо-

чения – по сложности и по нечеткости. Было бы желательно объединить их

неким подходящим образом. Поскольку для рассматриваемого типа задач

требуется, чтобы и сложность и порождающая нечеткость систем во множе-

стве решений Y

Q

, были минимизированы. Соответствующее объединенное

упорядочение

*

≤ определяется следующим образом:

B

j

B

i

FF

*

≤ тогда и только тогда, когда

MM

j

c

i

≤ и

u

j

u

i

qq ≤ , (В.61)

где

rB

j

B

i

YFF ∈,. Это упорядочение не является связным, поскольку пары

B

j

B

i

FF ,, для которых MM

ji

< и

u

j

u

i

qq > или MM

ji

> и

u

j

u

i

qq < (подоб-

ные пары, разумеется, могут существовать), несравнимы. Оно также неанти-

симметрично, так как не исключена возможность того, что

MM

ji

= и

u

j

u

i

qq =

для некоторых i ≠ j. Следовательно объединенное упорядочение – это общего

вида квазиупорядочение (рефлексивное и транзитивное отношение) на Y

r

.

Теперь множество решений Y

Q

можно определить как множество всех

систем из Y

r

, которые или эквивалентны, или несравнимы относительно объ-

единенного упорядочения (В.61). Две системы из Y

r

, скажем системы

B

i

F и

B

j

F , несравнимы в смысле обединенного упорядочения, если выполнено од-

но из следующих условий:

B

i

F более сложна и менее детерминирована, чем

B

j

F или

B

i

F менее

сложна и более детерминирована, чем

B

j

F . Формально

)})((|{

**

B

j

B

i

B

i

B

j

rB

j

rB

i

Q

FFFFYFYFY ≤⇒≤∈∀∈= . (В.62)

Системы из множества решений Y

Q

будем называть подходящими сис-

темами с поведением

для рассматриваемого типа задач.

Пример В.5 Чтобы пояснить различные вопросы, изучаемые в данном

разделе, рассмотрим этологическую систему данных, описанную в примере

В.2 (смотри также рисунок В.8). Определим все подходящие в смысле (В.62)

системы с поведением для этой системы данных в предположении, что поль-

зователь хочет получить описания вероятностных систем с поведением и

использовать их для предсказания.

Предположим сначала, что ∆

М = 2. Тогда имеется восемь содержатель-

217

ных масок, которые вместе с их упорядочением подмасок и указанием трех

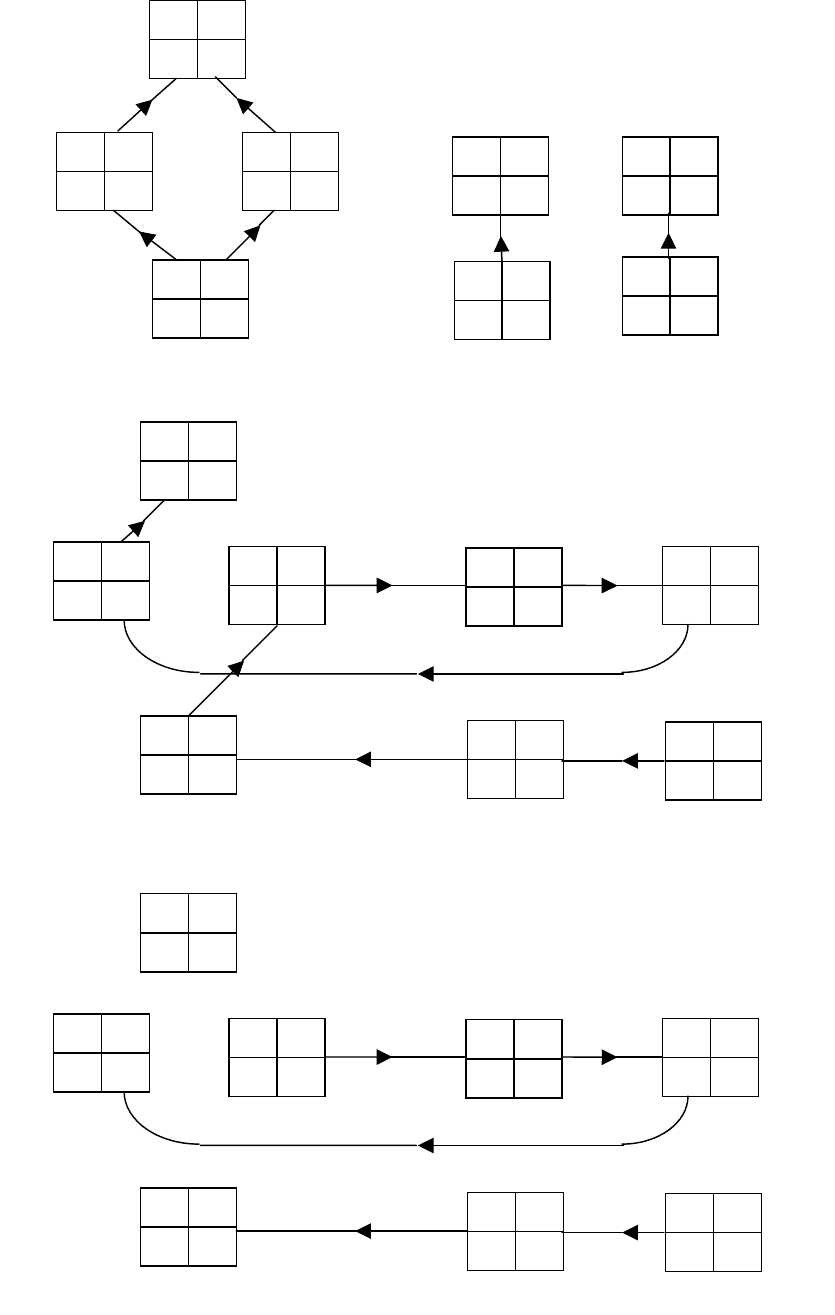
уровней сложности изображены на рисунке В.6а. После выполнения исчер-

пывающей выборки для наибольшей приемлемой маски

M

=

1

по опреде-

ленной пользователем формуле по частотам N(c) вычисляются вероятности

()

cf

B

, а порождающая нечеткость оценивается как вероятностная. Если для

вычисления вероятностей используется формула (В.42), то порождающая не-

четкость равна 1.11. Затем для остальных семи содержательных масок по

формуле (В.58) определяются соответствующие проекции и вычисляются их

порождающие нечеткости. Результаты этих вычислений показаны на рисунке

В.6б (в правом нижнем углу масок). На рисунке В.6б также изображено упо-

рядочение масок по нечеткости. В этом примере упорядочение является пол-

ным, поскольку значения нечеткости у всех разные. Объединенное упорядо-

чение по сложности и нечеткости (61) изображено на рисунке В.6в. Как мы

видим, минимальными с точки зрения объединенного упорядочения являют-

ся маски с идентификаторами 1,2,6. Следовательно, Y

Q

={

BBB

FFF

621

,,}.

Предположим теперь, что ∆

М = 3. Тогда имеется 40 содержательных

масок. После их обработки, аналогичной обработке для случая ∆

М = 2, мы

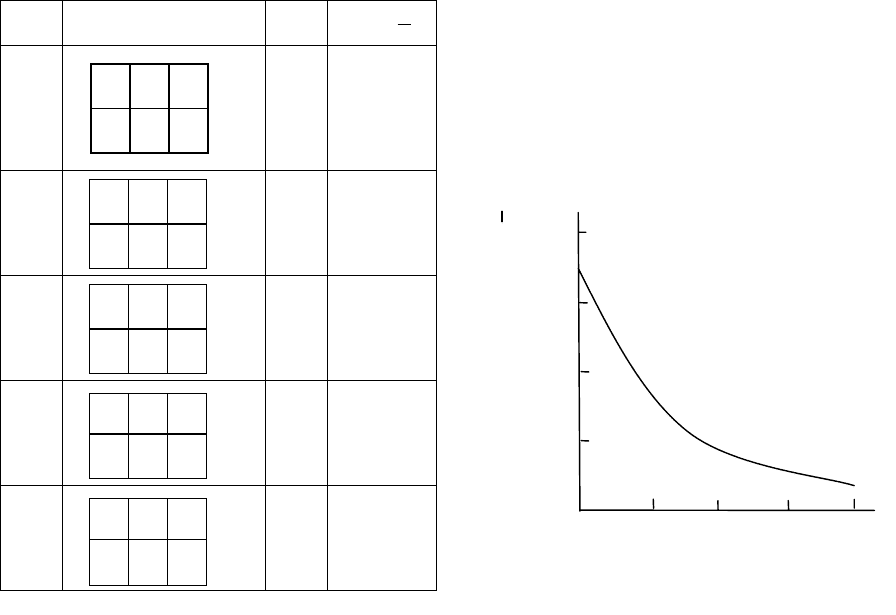
получим пять подходящих систем с поведением, маски которых, значения

сложности и порождающие нечеткости приведены на рисунке В.7а. остав-

шиеся 35 масок хуже с точки зрения их сложности, как и с точки зрения чет-

кости, и, следовательно, их вовсе не нужно рассматривать.

Описанный здесь поиск подходящих систем с поведением может быть

реализован самыми разными способами. Основной принцип заключается в

том, что содержательные маски получаются с помощью некоторого алгорит-

ма из наибольшей приемлемой маски в порядке уменьшающейся сложности.

Среди масок одинаковой сложности выбираются только маски с минималь-

ной порождающей нечеткостью. При этом если значение этой минимальной

нечеткости меньше или равно значению нечеткости для предшествующего

уровня сложности, то все ранее принятые системы отбрасываются. В резуль-

тате применения этой процедуры у нас остаются только подходящие систе-

мы.

Важно понимать, что задачи данной категории представляют собой тему

со многими вариациями. Например, можно многими разными способами вы-

числять вероятности или возможности, можно использовать разные опреде-

ления сложности, можно выдвинуть дополнительные условия, такие, как за-

дание наибольшей приемлемой четкости.

В.8 Порождающие системы

Термин «порождающая система» используется здесь в качестве общего

218

Рисунок В.6 – К примеру В.5

Объединенная упорядоченность

по сложности и по нечеткости

1

3

2

4

1

3

4

3

2

4

1

2

4

1

3

2

3

4

1

4

3

2

в

1

2

3

4

5

6

7

8

4

1.11

3

1.88

3

2.53

3

2.37

3

1.97

2

3.41

2

3.65

Упорядоченность по нечеткости

1

3

2

4

1

3

4

3

2

4

1

2

4

1

3

2

3

4

1

4

3

2

б

1

2

3

4

5

6

7

8

1.11

1.88

2.53

2.37

1.97

3.38 3.41

3.65

1

3

2

4

Упорядоченность подмасок

1

3

4

3

2

4

3

4

1

2

4

1

3

2

1

4

3

2

а)

1

2

3

6

4

7

5

8

2

3.38

219

i Маска i

|M|

)/( GGH

i

1

6

0.41

2

5

0.55

3

4

1.07

4

3

1.88

5

2

3.38

а) б)

Рисунок В.6 – Подходящие системы с поведением к примеру В.5

наименования для всех систем уровня 2 в эпистемологической иерархии сис-

тем. В этих системах обобщенное параметрически независимое ограничение

на рассматриваемые переменные описывается с разных сторон. Для порож-

дающих систем выделены различные методологические отличия. Это отли-

чия, выделенные для систем более низких уровней, и некоторые новые. Сре-

ди них наиболее существенными являются:

упорядоченность параметрического множества, что позволяет ввести

важное понятие маски;

упорядоченность множеств состояний, что играет существенную роль в

упрощении процедур для порождающих систем и при работе с неполностью

определенными наборами данных;

отличие четких и нечетких каналов наблюдения, дающих соответствен-

но четкие или нечеткие данные и требующих применения различных методов

обработки данных;

отличие между нейтральными и направленными системами, с которыми

следует обращаться по-разному.

Методологическими отличиями, относящимися к порождающим систе-

мам, но не к системам данных и исходным системам, являются:

детерминированность и недетерминированность систем;

для недетерминированных систем различаются типы нечетких мер, ха-

рактеризующих параметрически инвариантное ограничение на рассматри-

5

6

3

5

6

3

5

2

4

3

5

2

4

6

1

3

5

2

4

6

4

3

2

1

2

3

4

5

6

0

Нечеткость, i

H(G/G)

Сложность, || M

i

220

ваемые переменные, в частности меры вероятности и возможности;

по используемой маске различаются порождающие системы без памяти

и системы, зависящие от прошлого.

Разумеется, эти методологические отличия характеризуют и системы

более высоких эпистемологических уровней.

В.9 Упрощение порождающих систем

На некотором этапе обработки заданной системы данных часто жела-

тельно бывает упростить соответствующие этой системе порождающие сис-

темы. В некоторых случаях упрощения требует пользователь, для которого

существующие порождающие системы оказываются слишком сложными для

понимания. В других случаях упрощение требуется из-за предполагаемого

использования порождающих систем или по разным методологическим со-

ображениям.

Существует два основных метода одновременного упрощения систем

данных и соответствующих порождающих систем:

1) упрощение за счет исключения некоторых переменных из соот-

ветствующей подобной системы;

2) упрощение за счет определения классов эквивалентности состоя-

ний некоторых переменных.

Пусть множество переменных порождающей системы V состоит из n

переменных и любое подмножество V, за исключением пустого множества,

представляет содержательное упрощение первого рода. Следовательно, име-

ется 2

n

-2 нетривиальных упрощения первого рода. Они частично упорядоче-

ны по отношению «подмножество». Если для удобства включить исходное

множество V и пустое множество, то множество упрощений с частичным уп-

рощением образует решетку. Эту решетку называют

решеткой переменных

или

V-решеткой. По ней можно проводить упрощение порождающих систем,

подбираемых к соответствующим системам данных. Многочисленные при-

меры реального упрощения приведены далее...

В.10 Исследование и проектирование систем

Системные задачи могут возникать в двух основных контекстах: при ис-

следовании и при проектировании систем. Задачей

исследования систем яв-

ляется накопление знаний о различных наборах переменных и параметров,

определенных с конкретными целями на существующих объектах. Задачей

проектирования систем

является использование накопленных знаний для

создания новых объектов, для которых на специфицированные переменные

наложены определенные ограничения. Несмотря на то, что системные задачи

как при исследовании систем, так и при их проектировании существуют на

любом эпистемологическом уровне иерархии систем, в этом разделе ограни-

чимся рассмотрением задач, связанных с исходными системами, системами

данных и порождающими системами.

Миронов С.В., Пищухин А.М. Метасистемный подход в управлении

Подождите немного. Документ загружается.