Миронов С.В., Пищухин А.М. Метасистемный подход в управлении

Подождите немного. Документ загружается.

171

ние слова в тексте.

Если смысл свойств и баз и их взаимоотношения поняты правильно, то

ясно, как формально определить систему, заданную на объекте, иначе систе-

му объекта. Она представляет собой множество свойств, с каждым из кото-

рых связано множество его проявлений, и множество баз, с каждой из кото-

рых связано множество ее элементов.

Формально система объекта – это

(

)

{

}

{

}

(

)

mjjnii

NjBbNiAaО

∈

= |,,|, , (Б.1)

где

{}

,,...,2,1 nN

= а

{}

,...,2,1= ; a

и A

- соответственно свойство и множе-

ство его проявлений;

и B

- база и множество ее элементов; О – система

объекта.

Необходимо понимать, что система объекта может приобрести содержа-

ние только благодаря заданию конкретных процедур наблюдения или изме-

рения, с помощью которых создаются образы свойств. Таким образом, сис-

тема объекта должна рассматриваться как компонент большей системы; рас-

сматривать систему объекта саму по себе практически бесполезно.

Б.2 Переменные и параметры

Переменной здесь называется операционное представление свойства, то

есть образ свойства, определяемый конкретной процедурой наблюдения или

измерения. Каждая переменная имеет определенное имя (метку), отличаю-

щее ее от других, и связывается с определенным множеством величин, через

которые она себя проявляет. Эти величины обычно называют

состояниями

(или значениями) переменной, а все множество –

множеством состояний.

Аналогично

параметром называется операционное представление базы.

Каждый параметр имеет уникальное имя, и с ним связывается некое множе-

ство. Оно называется

параметрическим множеством, а его элементы – зна-

чениями параметра.

На отдельных множествах состояний или параметрических множествах

могут быть определены некоторые математические отношения, например,

отношения порядка или расстояние. Они отражают фундаментальные харак-

теристики свойств и баз в той степени, в какой они присущи соответствую-

щим измерительным процедурам. Различия в подобных свойствах среди пе-

ременных или параметров, которые имеют существенное методологическое

значение, называют

методологическими отличиями.

В дополнение к конкретным переменным и параметрам, представляю-

щим соответственно определенный признак или базу, рассматриваются так-

же

обобщенные переменные и параметры.

Обобщенной переменной дается интерпретация, когда множество ее со-

стояний отображается изоморфно (то есть отображается один в один с сохра-

нением всех существенных математических отношений, определенных на

нем) в элементы множества состояний конкретной переменной; то же отно-

сится к обобщенным и конкретным параметрам и их параметрическим мно-

172

жествам. Отображение такого рода называют конкретизацией обобщенной

переменной (или обобщенного параметра), а обратное отображение –

абст-

рагированием

конкретной переменной (или конкретного параметра).

Для формализации понятий обобщенных координат и конкретных пере-

менных и их параметров введем следующие обозначения: ,,

Vv V

–

соответственно обобщенная переменная, ее множество состояний и множест-

во математических свойств, определенных на

v . Обозначим через ,,

’

те

же характеристики конкретной переменной, являющиеся конкретизацией пе-

ременной

v . Обозначим через ,,

Ww W

соответственно обобщенный пара-

метр, его множество состояний и множество математических свойств, опре-

деленных на параметре ,

w а через

,,W

’

- те же характеристики кон-

кретного параметра, полученные конкретизацией параметра

w .

Назовем

каналом наблюдения любую операцию, вводящую конкретную

переменную как образ свойства. Канал наблюдения, с помощью которого

свойство

представляется переменной

, реализуется функцией

iii

VAo

→: . (Б.2)

Эта функция гомоморфна относительно предполагаемых свойств мно-

жеств

. Аналогичная функция

jjj

→

(Б.3)

задает представление базы

параметром

, она также должна быть гомо-

морфной относительно соответствующих свойств базы (например, времени)

и свойств множества

Б.3 Методологические отличия

Термин

методологическое отличие используется для выявления отли-

чий типов системных задач внутри одного эпистемологического уровня. Для

исходных систем методологические отличия касаются переменных и введен-

ных параметров.

Одним из фундаментальных методологических отличий является

от-

сутствие математических свойств

у множества состояний или соответст-

вующего параметрического множества. Такие, например, переменные как

семейное положение (одинокий, женатый, разведенный, вдовец),

политическая принадлежность (демократ, республиканец, независимый),

группа крови (А, В, О, АВ) или пол (мужской, женский), заданные на

элементах какой – либо общественной группы, демонстрируют

существенность этого методологического отличия.

Другим фундаментальным свойством множеств является

упорядочен-

ность

. Методологически следует различать два типа упорядоченности – час-

тичную и линейную.

Частичная упорядоченность – это бинарное отношение на множестве,

являющееся рефлексивным, антисимметричным и транзитивным.

Линейная

173

упорядоченность сильнее частичной, так как под ней понимается частичная

упорядоченность, обладающая свойством связности (то есть любая пара эле-

ментов множества так или иначе упорядочена).

Формально частичная упорядоченность Q, например, множества V

– это

бинарное отношение

VVQ

⊂ , (Б.4)

удовлетворяющее следующим требованиям:

1 Q)y,x(

∈ (рефлексивность);

2 если Q)y,x(

∈ и Q)x,y( ∈ , то x=y (антисимметричность);

3 если Q)y,x(

∈ и Q)z,y( ∈ , то Q)z,x(

∈

(транзитивность).

Если Q)y,x(

∈ , то x называется предшественником y, а y – преемником

x. Если Q)y,x( ∈ и не существует Qz

∈

, такого, что Q)z,x( ∈ и Q)x,z(

∈

, то

x называется

непосредственным предшественником y, а y – непосредствен-

ным преемником

x. В дополнение к требованиям рефлексивности, антисим-

метричности и транзитивности отношение линейной упорядоченности

удовлетворяет следующему требованию связности: для всех

V)y,x( ∈ , если

x≠y, то или Q)y,x(

∈ , или Q)х,y(

∈

Примерами переменных с частично упорядоченным множеством со-

стояний являются служебное положение или образование человека (опреде-

ленные, например, на группе государственных служащих). Примерами пере-

менных с линейно упорядоченными множествами состояний являются шкала

твердости Мооса, высота как характеристика звука или экзаменационные

оценки, определенные на группе студентов. Прекрасным примером упорядо-

ченности параметрического множества является время. Хотя в большинстве

случаев такое упорядочение линейно, имеют смысл и частично упорядочен-

ные временные множества, например при исследовании отдельных про-

странственно разделенных процессов (таких, как распределенные вычисли-

тельные машины, которые обмениваются друг с другом информацией и для

которых задержка при передаче сообщения сравнима со временем изменения

состояний переменных из отдельных процессов). Полезно определить упоря-

дочение и для некоторых групп. Например, группа людей может быть упоря-

дочена по таким отношениям, как «быть старше», «быть потомком», «зани-

мать более высокое положение по работе». Обычно частичные упорядочения

и их существенность зависит от характера группы и всего контекста задачи.

Переменные с линейно упорядоченными множествами состояний называют-

ся

переменными с упорядоченной шкалой.

Кроме частичных или линейных упорядочений существуют и другие

математические свойства, определение которых для множеств состояний или

параметрических множеств оказывается во многих случаях очень полезным.

Одним из наиболее существенных свойств является расстояние между парой

элементов изучаемого множества. Эта мера определяется функцией, сопос-

тавляющей любой паре элементов этого множества число, определяющее, на

каком расстоянии друг от друга находятся эти элементы с точки зрения неко-

174

торого фундаментального упорядочения.

Для данного множества, скажем множества

V , расстояние определяется

функцией δ вида

RVV

→

. (Б.5)

Однако для того, чтобы эта функция отвечала интуитивному представлению

о расстоянии, она должна удовлетворять следующим условиям для всех

Vzyx ∈,,:

()

0, ≥yx

(условие неотрицательности);

()

тогда и только тогда, когда х=у (условие нулевого рас-

стояния, называемое также условием невырожденности);

()

()()

xyyx ,,

(симметричность);

()

() ()()

zyyxzx ,,,

≤

(неравенство треугольника).

Любая функция, удовлетворяющая условиям

(

)

(

)

−

, называется мет-

рическим расстоянием

на множестве

V , а пара

(

)

V - метрическим про-

странством

. Метрическое расстояние можно, разумеется, определить как на

множестве состояний, так и на параметрическом множестве.

Примерами переменных с выраженными и существенными метриче-

скими расстояниями являются почти все переменные в физике, например

длина, масса, давление, электрическая проводимость, напряжение, сила зву-

ка, однако и помимо физики есть множество примеров таких переменных,

скажем, количество денег, объемы производства, число дефектов, число не-

счастных случаев и так далее. Совершенно очевидно, что и пространство, и

время – это параметры, к которым вполне естественно применимо понятие

метрического расстояния. Однако редко удается определить метрическое

расстояние на группах. Одним из таких примеров является группа студентов,

линейно упорядоченная по показателям их успеваемости. При этом расстоя-

ние для каждой пары студентов определяется как абсолютное значение раз-

ницы между их позициями в упорядоченном списке. Переменные, с множе-

ством состояний которых связано метрическое расстояние, обычно называ-

ются

метрическими переменными.

Еще одним свойством множеств состояний и параметрических мно-

жеств, имеющим большое значение как методологическое отличие, является

непрерывность. Это понятие хорошо известно из математического анализа, и

нет необходимости рассматривать его здесь подробно. Тем не менее уместно

будет привести несколько замечаний относительно некоторых аспектов не-

прерывности, которые будут использоваться нами в дальнейшем.

Необходимым условием непрерывности множества является его упоря-

доченность. Так как линейная упорядоченность является частным случаем

частичной упорядоченности, то предпочтительнее определить непрерывность

через частичную упорядоченность. Это можно сделать несколькими спосо-

бами. Одно из определений непрерывного частичного упорядочения опира-

ется на понятие разреза частично упорядоченного множества:

разрез частич-

но упорядоченного множества,

скажем множества

V , это разделение этого

175

множества на два непустых подмножества, например

и XVY

−= , такое,

что или никакой элемент

не является предшественником (согласно час-

тично упорядочению, определенному на

V ) никакого элемента из

и некий

элемент

является предшественником какого-либо элемента

, или ника-

кой элемент из

не является преемником никакого элемента из

и некото-

рый элемент

является преемником некоторого элемента

. Непрерывное

частичное упорядочение

V определяется как частичное упорядочение, для

которого любой разрез

множества

V характеризуется неким элементом

из

, являющимся предшественником элемента из

, такого, что или наи-

большая верхняя граница

принадлежит

, или наименьшая нижняя грани-

ца

принадлежит

Наилучшим примером непрерывного частичного упорядочения являет-

ся отношение «меньше или равно», определенное на множестве действитель-

ных чисел или на его декартовых произведениях. Фактически само понятие

непрерывной переменной (или непрерывного параметра) опирается на требо-

вание, чтобы соответствующее множество состояний (или параметрическое

множество) было изоморфно множеству действительных чисел.

Из этого следует, что множество состояний любой непрерывной пере-

менной или параметрическое множество любого параметра бесконечно и не-

счетно. Тем самым альтернативой непрерывным переменным и параметрам

являются переменные и параметры, заданные на конечных множествах или,

возможно. На бесконечных счетных множествах. Последние называются

дискретными переменными или параметрами.

Непрерывные переменные и параметры представляются действитель-

ными числами, а их дискретные аналоги удобно представлять целыми числа-

ми. Это особенно существенно, если множество состояний или параметриче-

ское множество значений дискретной переменной или параметра линейно

упорядочено и, следовательно, изоморфно соответствующим множествам

значений целых чисел. Для работы с некоторыми переменными и параметра-

ми могут быть использованы метрическое расстояние, определяемое естест-

венным образом как абсолютное значение разницы между целыми, а также

целая арифметика.

Для нас такие свойства. Как упорядоченность, метрическое расстояние

и непрерывность множеств состояний и параметрических множеств, пред-

ставляют основу для определения наиболее существенных методологических

отличий на уровне переменных и параметров. Приведем список перенумеро-

ванных альтернатив для этих свойств:

Упорядоченность: 0 – упорядоченности нет

1 – частичная упорядоченность

2 – линейная упорядоченность

Расстояние: 0 – не определено

1 – определено

Непрерывность: 0 – дискретно

1 – непрерывно

176

Статус любой переменной (или параметра) для этих трех свойств мо-

жет быть однозначно охарактеризован триплетом - упорядоченность, рас-

стояние, непрерывность, в котором каждое свойство представляется его оп-

ределенным значением (или его идентификатором). Так, например, триплет

(2, 1, 0) описывает дискретную переменную с линейно упорядоченным мно-

жеством состояний, на котором определено метрическое расстояние.

Хотя данные три свойства в принципе определяют 12 возможных ком-

бинаций, три из них (0, 0, 1), (0, 1, 0) и (0, 1, 1) смысла не имеют. В самом де-

ле, если на множестве не определена упорядоченность, то на нем нельзя ни

содержательно определить метрическое расстояние, ни рассматривать его как

непрерывное. Таким образом, имеется девять осмысленных комбинаций. Бу-

дем называть эти комбинации

методологическими типами переменных и па-

раметров. Они могут быть частично упорядочены с помощью отношения

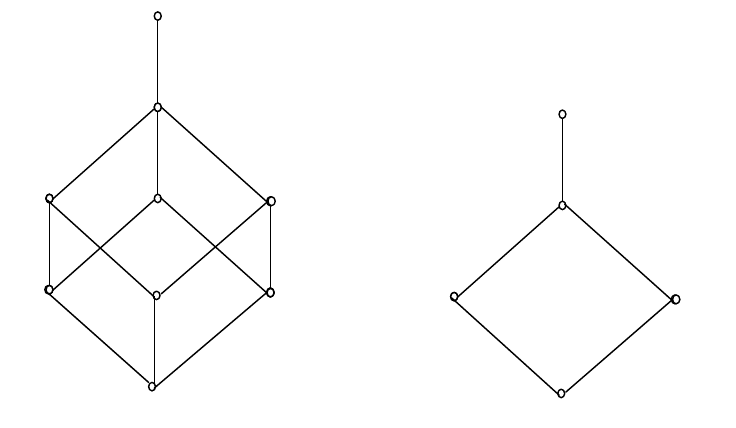
«быть методологически более определенным чем». На рисунке Б.2(а) это

частичное упорядочение, образующее решетку, представлено в виде диа-

граммы Хассе. Упрощенная решетка на рисунке Б.2(б) задает схему для

свойств упорядоченности и расстояния, но без непрерывности.

а) б)

Рисунок Б.2 - Решетки методологических типов переменных или пара-

метров

На уровне переменных и параметров методологическое отличие одной

переменной представляет собой сочетание методологических типов этой пе-

ременной и соответствующих баз. Каждая из них имеет девять типов. Следо-

вательно, если есть только одна база или требуется, чтобы все базы, входя-

щие в комбинацию, имели один методологический тип (наиболее часто

встречающийся случай), то число методологических отличий будет равно 81

(так как методологические типы переменных и параметров не накладывают

ограничений друг на друга). Если к тому же в нашей схеме будут учитывать-

ся только дискретные переменные и параметры, методологические типы ко-

торых приведены на рисунке Б.2(б), то число методологических отличий со-

кратится до 25. Решетка методологических отличий для этого случая приве-

дена в таблице Б.1.

200

201

211

210

110

101

100

000

20 11

177

Теперь предположим, что имеется два или более, например m, парамет-

ров. Они могут быть одного, двух, трех (независимо от порядка) и так далее.

Таблица Б.1- Решетка методологических отличий для дискретных перемен-

ных и параметров

Методологическое отли-

чие

Непосредственные предшественники в решетке

00/00 10/00 00/10

00/10 10/10 00/20 00/11

00/20 10/20 00/21

00/11 10/11 0/21

00/21 10/21

10/00 20/00 11/00 10/10

10/10 20/10 11/10 10/20 10/11

10/20 20/20 11/20 10/21

10/11 20/11 11/11 10/21

10/21 20/21 11/21

20/00 21/00 20/10

20/10 21/10 20/20 20/11

20/20 21/20 20/21

20/11 21/11 20/21

20/21 21/21

11/00 11/10 21/00

11/10 11/20 11/11 21/10

11/20 11/21 21/20

11/11 11/21 21/11

11/21 21/21

21/00 21/10

21/10 21/20 21/11

21/10 21/21

21/11 21/21

21/21 none

Предположим, что m ≤ 9 (это довольно разумное предположение), тогда об-

щее число методологических типов полного параметра определяется суммой





































...

. (Б.6)

типов.

При сочетании этой суммы с девятью методологическими типами пе-

ременных мы получим общее число возможных методологических отличий

одной переменной и ее параметра, это число определяется формулой

∑













9 . (Б.7)

178

Б.4 Представляющие и исходные системы

Свойства, конкретные и общие переменные, а также базы, конкретные и

общие параметры являются компонентами соответственно трех примитив-

ных систем – системы объекта, конкретной представляющей (image) системы

и общей представляющей системы, которые вместе с отношениями между

ними образуют исходную систему. Одна из этих трех систем введена в раз-

деле Б.1 и формально определяется уравнением (Б.1). Оставшиеся две при-

митивные системы имеют тот же вид, что и система объекта, но их компо-

нентами являются переменные и параметры, а не свойства и базы.

Пусть İ и I – это, соответственно конкретная и общая представляющая

системы. Тогда

{

(

)

}

,|,

nii

NiVI ∈=

(

)

})

{

mjj

NW ∈|,

, (Б.8)

(

)

{

}

(

nii

NiVI

∈

(

)})

{

mii

NjW

∈

, (Б.9)

где соответствующие символы имеют тот же смысл, что и в разделе Б.2.

Теперь нужно определить отношения между тремя примитивными сис-

темами O, İ, I. Для упрощения нотации условимся, что для любых

∈

Mj ∈ свойство

a соответствует переменным

ϑϑ

, а база

b - парамет-

рам

Отношение между системой объекта и конкретной представляющей

системой задается в виде полного канала наблюдения, состоящего из отдель-

ных каналов наблюдения, по одному для каждого свойства или базы из сис-

темы объекта. Обозначим через

Q четкий полный канал наблюдения. Тогда

(

)

{

(

,|,,

niii

NioVAQ ∈=

о (Б.10)

определяется уравнением (Б.2) и должны быть

гомоморфны относительно

свойств

A и

}

(

)

{

mjjj

NjWB ∈|,,

определяются уравнением (Б.3) и

должны быть

гомоморфны относительно свойств

B и

}

)

, где все символы

имеют тот же смысл, что и в разделе Б.2.

Нечеткий полный канал наблюдения, скажем Q

, можно получить, заме-

нив

из (Б.10) на

, определенное совместно со степенью достоверности.

Функции

также можно было бы заменить на функции

, также опреде-

ленные с некоторой степенью достоверности.

Отношение между конкретной и общей представляющими системами

задаются набором отображений конкретизации (абстрагирования, по одному

для каждой переменной и параметра из этих систем). Будем называть этот

набор

каналом конкретизации / абстрагирования и обозначать его

. Тогда

{()

niii

NieVVE ∈= |,,

e определяют переход от обобщенных переменных к

конкретным и должны быть

изоморфны относительно свойств

}

V ,

(

)

{

mjjj

NjWW ∈|,,

определяют переход от обобщенных параметров к

конкретным и должны быть изоморфны относительно свойств

}

)

W .

179

Можно рассмотреть канал наблюдения из системы объекта непосредст-

венно в общую представляющую систему. Однако этот канал можно полу-

чить из двух каналов. Он состоит из триплетов

(

)

−

iiii

OeoVA и

(

)

−

jjjj

OWB

εϖ

где символ О обозначает композицию.

Теперь можно определить

исходную систему, как пятерку

S = (O, İ, I, Q, E). (Б.11)

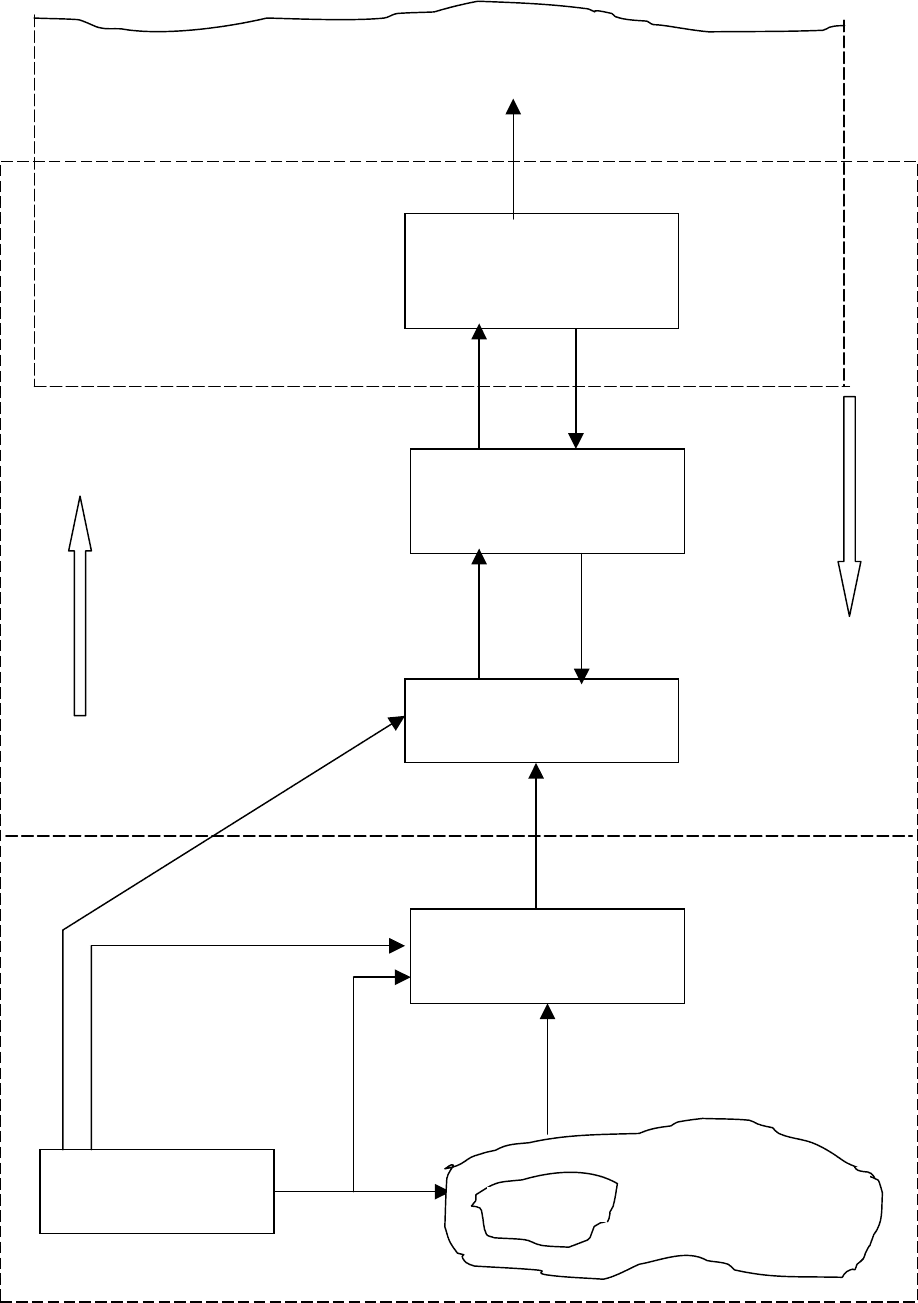
На рисунке Б.3 изображены эти пять компонентов, а также их связи с

дометодологическими посылками (исследователь, объект, цель исследования

и так далее) и с системами более высоких эпистемологических уровней. Ри-

сунок также дает представление об основных методологических понятиях,

связанных с исходной системой:

1 С одной стороны, исходная система представляет связи с реальным

миром. Они проходят через систему объекта

О и канал наблюдения Q. С дру-

гой стороны, исходная система связана с

универсальным решателем систем-

ных задач

(УРСЗ) через общую представляющую систему I и канал конкре-

тизации / абстрагирования

Е. Эти два компонента (I и Е) представляют ин-

терфейс между конкретной предметной областью и УРСЗ. Данный интер-

фейс, находящийся на самом нижнем эпистемологическом уровне, очень ва-

жен, поскольку любой интерфейс на более высоком уровне опирается на не-

го.

2 По существу концептуальная схема УРСЗ – это специальный язык

для описания важных системных задач. Область УРСЗ ограничена

синтакси-

ческими аспектами

решения системных задач. Эти аспекты представляются

через разные методологические отличия общих представляющих систем и их

эпистемологически более высоких аналогов. Таким образом, реализация

УРСЗ может быть разработана и описана только в терминах общих представ-

ляющих систем и их развития на более высоких эпистемологических уров-

нях. При применении УРСЗ в конкретном исследовании или для какой-то

180

Рисунок Б.3 – Концептуальные элементы, используемые для определения ис-

ходной системы

СИСТЕМЫ ЭПИСТЕМОЛОГИЧЕСКИ БОЛЕЕ

ВЫСОКИХ УРОВНЕЙ

ИСТОЧНИК ДАННЫХ

ОБОБЩЕННАЯ

ПРЕДСТАВЛЯЮЩАЯ

СИСТЕМА

КОНКРЕТНАЯ

ПРЕДСТАВЛЯЮЩАЯ

СИСТЕМА

ОБЪЕКТА О

ДОМЕТОЛОГИЧЕСКИЕ

ПРЕДПОСЫЛКИ

ФОРМАЛИЗАЦИЯ ИС-

ХОДНОЙ СИСТЕМЫ

ВЫБОР

• признаков

•

баз

Допустимые и уместные взаимо-

действия

ИССЛЕДОВАТЕЛЬ

ИЛИ ГРУППА ИС-

СЛЕ

ОВАТЕЛЕЙ

ОБЪЕКТ

СРЕДА ИССЛЕДО-

ВАНИЯ

• Цель

исследования

• Ограничения

на исследование

(прагматические

КАНАЛ НА-

БЛЮДЕНИЯ

ИСХОДНАЯ

СИСТЕМА S

АБСТРАГИРОВАНИЕ

(семантические аспекты)

Уравнение

(2.11)

Уравнение (2.13)

Уравнение

(2.1)

ИНТЕРПРЕТАЦИЯ

(семантические ас-

пекты)

УРАВНЕНИЕ

()

Уравнение

(2.12)

ИНТЕРФЕЙС

С УРСЗ

КАНАЛ КОНКРЕТИЗАЦИИ /

АБСТРАГИРОВАНИЯ

УРСЗ

(синтаксические

объекты)