Mikles J., Fikar M. Process Modelling, Identification, and Control

Подождите немного. Документ загружается.

452 10 Adaptive Control

G(s)=

b(s)

a(s)

s + b

+ a

s + a

(10.8)

This system will be controlled by an adaptive feedback controller accord-

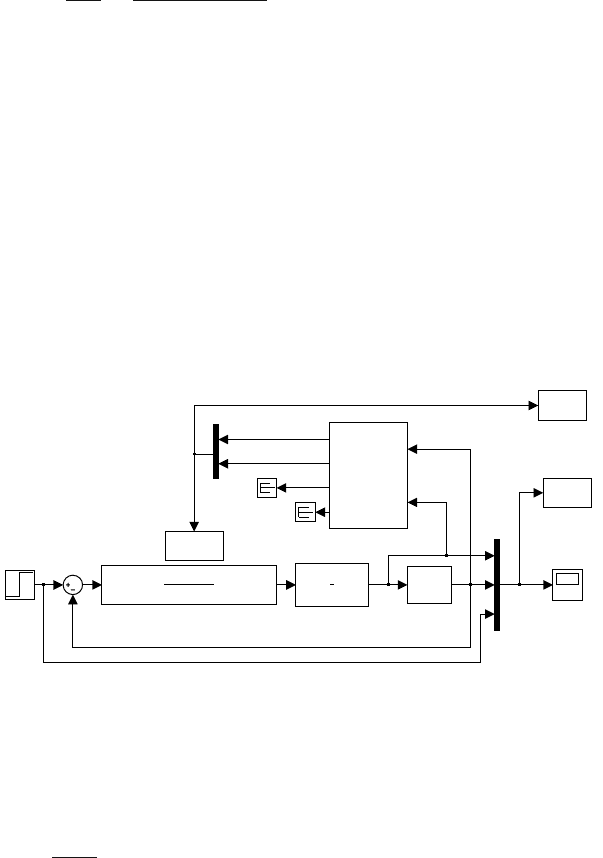
ing to the Simulink scheme ad033s.mdl shown in Fig. 10.5. Initialisation of

this diagram is performed with the script ad033init.m that sets the process,

identiﬁcation and controller update sampling time. This ﬁle can be loaded

automatically in the same way as in the previous example by the command

set_param(’ad031s’, ’PreLoadFcn’, ’ad031init’);

Program 10.3 (Initialisation of the scheme in Fig. 10.5 – ﬁle)

ad033init.m

ts = .5;

G = tf([1 1.5],[1 3 2]);

param

To Workspace1

data

To Workspace

Step

Scope

stconcon

ST continuous

controller design

Process

Pred. error

Integrator

Cov. matrix

.1s +.4s+.2

.1s +.7s+.2

Controller

C−identification

SISO

Continuous identification

Fig. 10.5. Scheme ad0313.mdl in Simulink for LQ tracking of a continuous-time

second order system with a continuous-time adaptive controller

Parameters a

, a

, b

are estimated in the each sampling time. The

feedback LQ control law based on state observation is given as

u = −

q(s)

sp(s)

e (10.9)

where the polynomials

q(s)=q

+ q

s + q

,p(s)=p

+ p

s + p

(10.10)

are solution of the Diophantine equation

a(s)sp(s)+b(s)q(s)=o(s)f(s) (10.11)

Polynomials

10.3 Examples of Self-Tuning Control 453

o(s)=s

+ o

s + o

,f(s)=s

+ f

s + f

(10.12)

are stable and monic and f(s) is deﬁned by the spectral factorisation equation

˜a(−s)˜a(s)+

(−s)

(s)=f(−s)f(s) (10.13)

where

˜a(s)=sa(s),

(s)=˜a(s)(sI −A

)

−1

(10.14)



0 I

0 A



, B





(10.15)

A =



−a



, B =





(10.16)

Weighting matrix

of the form



Q 0



(10.17)

follows from the cost function to be minimised

I =



∞



Qx +˙u



dt (10.18)

where

Q =



0 Q



(10.19)

Coeﬃcients of the control law are determined in each sampling instant from

equation (10.11) based on estimated parameters a

, a

, b

. Finally, the

control action is realised.

Parameter estimation is for the case shown in Fig. 10.5 implemented using

the continuous-time SISO identiﬁcation block from the library IDTOOL and

the controller parameters are calculated in the S-function stconcon.

MATLAB function set_param is used to transfer the calculated controller

parameters into the block Controller and thus to close the adaptive control

loop. The implementation is as follows.

Program 10.4 (S-funkcia stconcon.m)

function [sys,x0,str,ts] = stconcon(t,x,u,flag,tsamp)

switch flag,

case 0,

[sys,x0,str,ts]=mdlInitializeSizes(tsamp);

case 2,

sys=mdlUpdate(t,x,u);

case 3,

454 10 Adaptive Control

sys=mdlOutputs(t,x,u);

case 9,

sys=mdlTerminate(t,x,u);

otherwise

error([’Unhandled flag = ’,num2str(flag)]);

end

function [sys,x0,str,ts]=mdlInitializeSizes(tsamp)

sizes = simsizes;

sizes.NumContStates = 0;

sizes.NumDiscStates = 0;

sizes.NumOutputs = 0;

sizes.NumInputs = 5;

sizes.DirFeedthrough = 1;

sizes.NumSampleTimes = 1;

sys = simsizes(sizes);

x0 = [];

str = [];

ts = [tsamp 0];

% Controller initialisation

Denominator = ’[.1 .7 .2]’;

Numerator = ’[.1 .4 .2]’;

set_param(’ad033s/Controller’, ’Numerator’, Numerator, ...

’Denominator’, Denominator);

function sys=mdlOutputs(t,x,u)

if t>4 % begin adaptive control

b1 = u(1); b0 = u(2); b = b1*s + b0;

a2 = u(3); a1 = u(4); a0 = u(5); a = a2*s^2 + a1*s + a0;

An=[0 0 1 0;0 0 0 1;0 0 0 1;0 0 -a0 -a1];

Bn=[0;0;0;1];

Cn=[b0 b1 0 0];

[BRs,AR]=ss2rmf(An,Bn,eye(4));

BR=Cn*BRs;

Q1=1; Q2=1;

Qn=[Q1 0 0 0;0 Q2 0 0;0 0 0 0;0 0 0 0];

[Dc,J]=spf(AR’*AR+BRs’*Qn*BRs);

Df=s^2+1.5*s+3;

[x0,y0]=axbyc(AR,BR,Dc*Df);

tt = 0;

xx=x0-b*tt;

yy=y0+a*tt;

10.3 Examples of Self-Tuning Control 455

Denominator = sprintf(’[%f %f %f]’,xx{2},xx{1},xx{0});

Numerator = sprintf(’[%f %f %f]’,yy{2},yy{1}, yy{0});

set_param(’ad033s/Controller’, ’Numerator’, Numerator, ...

’Denominator’, Denominator);

end

sys=[];

function sys=mdlUpdate(t,x,u)

sys = [];

function sys=mdlTerminate(t,x,u)

sys = [];

0 5 10 15 20

0.5

1.5

2.5

(a)

u,y,w

0 5 10 15 20

−0.5

0.5

1.5

(b)

Param

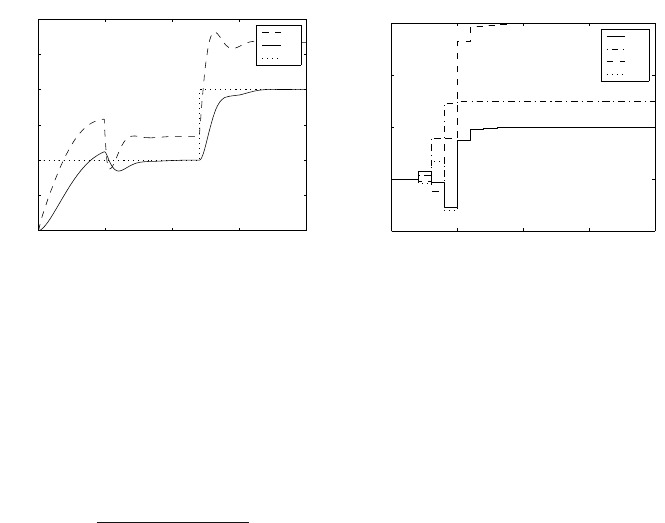
Fig. 10.6. Trajectories of (a) input, output, and setpoint variables, (b) identiﬁed

parameters of the continuous-time process model controlled with LQ controller

Fig. 10.6a shows trajectories of input and output variables of the controlled

process and Fig. 10.6b gives the trajectories of the estimated parameters. ID-

TOOL normalises the estimated transfer function, thus a

= 1. LQ weighting

coeﬃcients were set as ϕ =1,ψ = 10.

The nominal controller and the observer polynomial were set as

R(s)=

0.1s

+0.4s +0.2

0.1s

+0.7s +0.2

,o(s)=s

+1.5s + 3 (10.20)

The adaptive closed-loop system was controlled in the ﬁrst eight sampling

periods (T

=0.5) with this nominal controller. Afterwards, the controller

calculated in the block stconcon was used. The choice of the sampling period

follows from the dynamical properties of the process. The controlled process

used in the simulation was the same as its model.

456 10 Adaptive Control

10.3.3 Continuous-Time Adaptive MIMO Pole Placement Control

Consider a continuous-time multivariable controlled system with the transfer

function matrix

www

G(s)=A

−1

(s)B

(s) (10.21)

where

(s)=



1+a

s 1+a



, B

(s)=





(10.22)

and a

= a

Nonadaptive LQ control of this system was illustrated in Example 8.11 on

page 386.

This system will be controlled by an adaptive feedback controller accord-

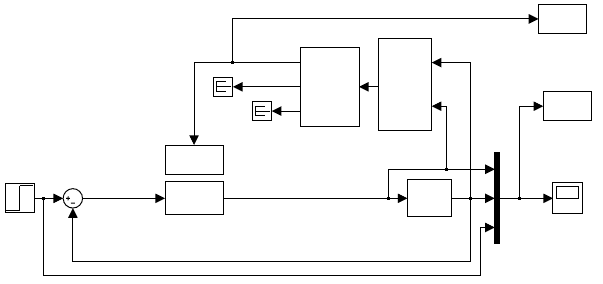
ing to the Simulink scheme ad035s.mdl shown in Fig. 10.7. Initialisation of

this diagram is performed with the script ad035init.m that sets the process,

integrator, identiﬁcation and controller update sampling time. This ﬁle can

be loaded automatically in the same way as in the previous example by the

command

set_param(’ad035s’, ’PreLoadFcn’, ’ad035init’);

Program 10.5 (Initialisation of the scheme in Fig. 10.7 – ﬁle)

ad035init.m

ts = 0.5;

al = [1+.3*s, .5*s; .1*s 1+0.7*s];

bl = [.2 .4;.6 .8];

bl = pol(bl);

[a,b,c,d] = lmf2ss(bl,al);

G = ss(a,b,c,d);

Parameters of the left matrix fraction a

are estimated in each sampling

instant.

To calculate the controller, it is necessary to determine the right matrix

fraction of the controlled process

−1

(s)B

(s)=B

(s)A

−1

(s) (10.23)

The feedback controller

R(s)=P

−1

(s)Q(s)=





−1



+ q

s + q



(10.24)

is then obtained by solving the matrix Diophantine equation

(s)A

(s)+Q

(s)B

(s)=

(s)F

(s) (10.25)

where the matrix

(s)F

(s) determines poles of the closed-loop system.

10.3 Examples of Self-Tuning Control 457

param

To Workspace1

data

To Workspace

Step

Scope

st2i2ocon

ST MIMO continuous

controller design

Process

Pred. error

LDDIF

Lddif

Cov. matrix

x’ = Ax+Bu

y = Cx+Du

Controller

C−filter

Continuous

filter

Fig. 10.7. Scheme ad035s.mdl in Simulink for tracking of a multivariable system

with a continuous-time adaptive controller

Parameter estimation is for the case shown in Fig. 10.7 implemented us-

ing the blocks from the library IDTOOL and the controller parameters are

calculated in the S-function st2i2ocon.

MATLAB function set_param is used to transfer the calculated controller

parameters into the block Controller and thus to close the adaptive control

loop. The implementation is as follows.

Program 10.6 (S-funkcia st2i2ocon.m)

function [sys,x0,str,ts] = st2i2ocon(t,x,u,flag,tsamp)

switch flag,

case 0,

[sys,x0,str,ts]=mdlInitializeSizes(tsamp);

case 2,

sys=mdlUpdate(t,x,u);

case 3,

sys=mdlOutputs(t,x,u);

case 9,

sys=mdlTerminate(t,x,u);

otherwise

error([’Unhandled flag = ’,num2str(flag)]);

end

function [sys,x0,str,ts]=mdlInitializeSizes(tsamp)

sizes = simsizes;

sizes.NumContStates = 0;

sizes.NumDiscStates = 0;

sizes.NumOutputs = 0;

sizes.NumInputs = 8;

sizes.DirFeedthrough = 1;

458 10 Adaptive Control

sizes.NumSampleTimes = 1;

sys = simsizes(sizes);

x0 = [];

str = [];

ts = [tsamp 0];

% Controller initialisation

A=’[0 0; 0 0]’;

B=’[1 0; 0 1]’;

C=’[1 0;0 1]’;

D=’[.1 .1 ; .1 .1]’;

set_param(’ad035s/Controller’, ...

’A’, A, ’B’, B, ’C’, C, ’D’, D);

function sys=mdlOutputs(t,x,u)

if t>4 % begin adaptive control

al = [1+u(1)*s, u(2)*s; u(5)*s, 1+u(6)*s];

bl = pol([u(3), u(4); u(7), u(8)]);

[br,ar] = lmf2rmf(bl,al);

ar = ar * s; % add integrator

% closed-loop poles

clpoles = [(0.7*s+1)*(1.5*s+1),0;0,(0.7*s+1)*(1.5*s+1)];

[pl,ql]=xaybc(ar, br, clpoles);

[ac,bc,cc,dc] = lmf2ss(ql,pl*s);

A = sprintf(’[%f %f; %f %f]’,ac’);

B = sprintf(’[%f %f; %f %f]’,bc’);

C = sprintf(’[%f %f; %f %f]’,cc’);

D = sprintf(’[%f %f; %f %f]’,dc’);

set_param(’ad035s/Controller’, ...

’A’, A, ’B’, B, ’C’, C, ’D’, D);

end

sys=[];

function sys=mdlUpdate(t,x,u)

sys = [];

function sys=mdlTerminate(t,x,u)

sys = [];

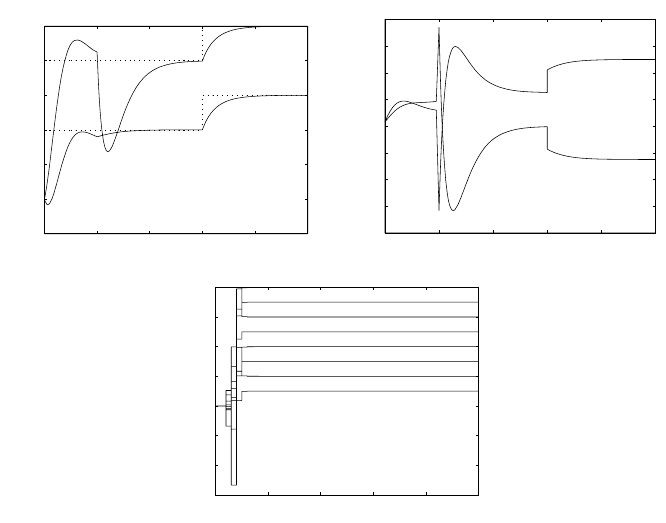
Fig. 10.6a,b shows trajectories of input and output variables of the

controlled process and Fig. 10.6c gives the trajectories of the estimated

parameters.

The nominal controller and the closed-loop poles were set as

10.3 Examples of Self-Tuning Control 459

0 5 10 15 20 25

−0.5

0.5

1.5

2.5

(a)

y,w

0 5 10 15 20 25

−8

−6

−4

−2

(b)

0 5 10 15 20 25

−0.6

−0.4

−0.2

0.2

0.4

0.6

0.8

(c)

Param

Fig. 10.8. Trajectories of (a) output, and setpoint variables, (b) input variables, (c)

identiﬁed parameters of the continuous-time process controlled with a pole placement

controller

R(s)=



s 0

0 s



−1



1+0.1s 0.1s

0.1s 1+0.1s



(10.26)

(s)F

(s)=(0.7s + 1)(0.5s +1)I (10.27)

The adaptive closed-loop system was controlled in the ﬁrst eight sampling

periods (T

=0.5) with this nominal controller. Afterwards, the controller

calculated in the block st2i2ocon was used. The controlled process used in

the simulation was the same as its model.

10.3.4 Adaptive Control of a Tubular Reactor

This example dealing with the control of a tubular chemical reactor describes

the adaptive implementation of GPC. A linear model is estimated on-line with

a recursive least squares algorithm and successively controlled.

We consider an ideal plug-ﬂow tubular chemical reactor with an exothermic

consecutive reaction A → B → C in the liquid phase and with countercurrent

cooling. It is assumed that A is the educt, B is the desired product and C the

460 10 Adaptive Control

unwanted by-product of the reaction. Such reactors are central components of

many plants in the chemical industry and exhibit highly nonlinear dynamics.

Mathematical model of this reactor is given as

∂c

∂t

= −v

∂c

∂z

− k

(10.28)

∂c

∂t

= −v

∂c

∂z

− k

(10.29)

∂T

∂t

= −v

∂T

∂z

ρc

−

ρc

(T − T

) (10.30)

∂T

∂t

− d

)ρ

(T − T

)+d

− T

)] (10.31)

∂T

∂t

= v

∂T

∂z

− n

)ρ

− T

) (10.32)

with initial conditions

(z,0) = c

(z),T(z,0) = T

(z),T

(z,0) = T

(z)

(z,0) = c

(z),T

(z,0) = T

(z)

(10.33)

and with boundary conditions

(0,t)=c

(t),T(0,t)=T

(t)

(0,t)=c

(t),T

(L, t)=T

(t).

(10.34)

Here t is time, z space variable along the reactor, c are concentrations, T are

temperatures, v are ﬂuid velocities, d are diameters, ρ are densities, c

are

speciﬁc heat capacities, and U are heat transfer coeﬃcients. The subscripts

are (.)

for metal wall of tubes, (.)

for coolant, and (.)

for steady-state

values. The reaction rates k and the heat of reactions are expressed as

= k

exp(−E

/RT ) ,j=1, 2 (10.35)

= h

+ h

(10.36)

where k

are exponential factors, E are activation energies and h are reaction

enthalpies.

Assuming the reactant temperature measurement along the reactor at

points z

, the mean temperature proﬁle can be expressed as

(t)=



j=1

T (z

,t) (10.37)

where n is the number of measured temperatures along the reactor.

The input variable, the value of q

, has been assumed to be constrained in

the interval

0.2 ≤ q

≤ 0.35 (10.38)

10.3 Examples of Self-Tuning Control 461

For the control purposes both the manipulated input and the controlled

output were deﬁned as scaled deviations from their steady-state values

u(t)=

(t) −q

,y(t)=

(t) −T

. (10.39)

This scaling helps to obtain variables with approximately the same magnitude

and reduces the possibility of ill-conditioned control problem and round-oﬀ

errors.

The sampling time was chosen T

=3s and the reactor was on-line iden-

tiﬁed as SISO discrete system with deg(A)=2, deg(B)=3oftheform

y(k)=−a

y(k−1)−a

y(k−2)+b

u(k−1)+b

u(k−2)+b

u(k−3)+d

+ξ

(10.40)

The estimation method used is the recursive least-squares algorithm LDDIF

with exponential and directional forgetting. The value of exponential forget-

ting was set at 0.8 and the minimum of the covariance matrix was constrained

to 0.01I. The purpose of these settings was to improve tracking properties of

the estimation algorithm.

The result of the ﬁrst simulation is shown in Fig. 10.9. It shows comparison

of two GPC settings: mean-level (ml) and dead-beat (db) control.

The upper graph represents behaviour of the controlled variable T

to-

gether with its reference value and the lower graph manipulated variable q

The values of GPC tuning parameters [N

,λ] were [1, 15, 1, 10

−1

]

for mean-level and [3, 7, 3, 10

−5

] for dead-beat, respectively. These values cor-

respond to the slow open loop response (ml) and the fastest dead-beat re-

sponse. The polynomials P, C were set to 1 as the eﬀect of disturbances is

very small. One can notice that the dead-beat control strategy actively uses

constraints on manipulated variable deﬁned by Eq. (10.38).

The purpose of the second simulation was to investigate the behaviour

of GPC with respect to unmeasured disturbances. The output variable was

corrupted by measurement noise with variance 0.1K. The inlet concentration

of the component A varied in steps and was given as

0 100 300 500

− c

0 0.1 0 0.1

Due to the presence of disturbances, the design polynomials P,C were

used. The polynomial C attenuates eﬀects of measurement noise and the

polynomial P shapes responses of the closed-loop system subject to load

disturbances in c

and also to reference step changes. The degrees of the

polynomials were chosen 1 and their values as

P =0.6 −

−1

,C=1− 0.8z

−1

. (10.41)

The GPC controller was implemented with the mean-level strategy and had

the values of the tuning parameters given as [1, 15, 1, 10

−1