Meyer Franz. A Handbook of Ornament
Подождите немного. Документ загружается.

GEOMETRICAL MOTIVES.
31
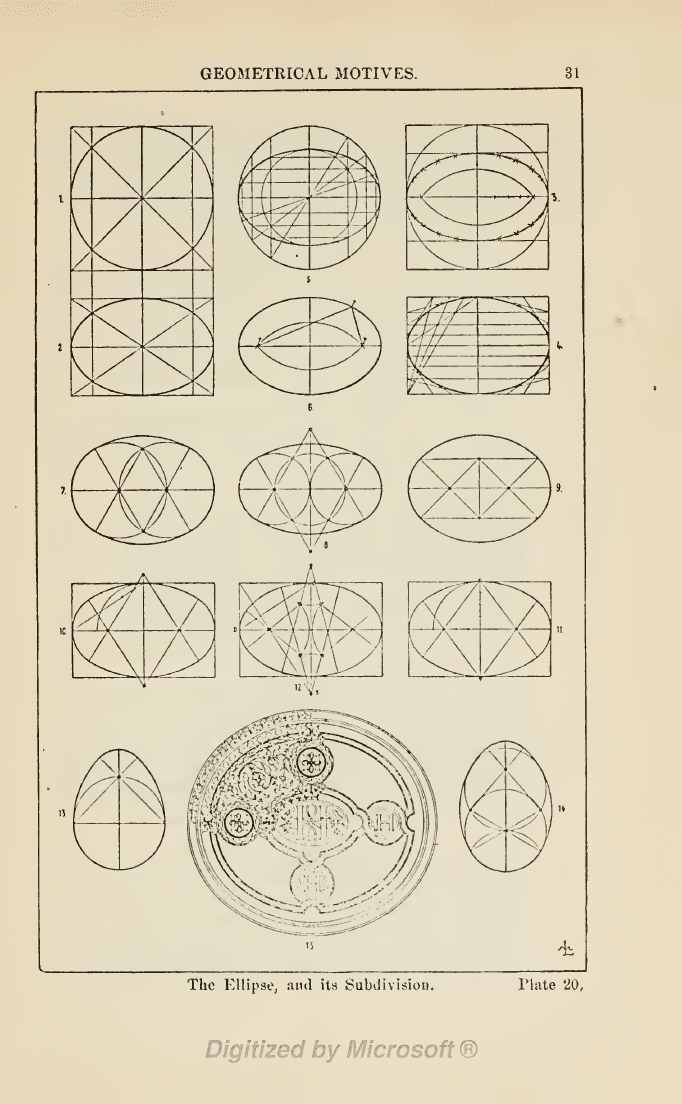
The Ellipse, and its
Subdivisiou. Plate
20,

32
The
ElliDse.
the transverse and
conjugate
axes; join tlie ends* of the
axes in
one of the
quarters by a
diagonal;
and
set-off a number
of
points
on this
diagonal. Through
these
points
draw straight
lines
from
the
opposite angle,
and also
parallels to the longitudinal
axis.
Now
join
the
points
thus
obtained
on the
outside
of the quarters
in the
way
shown in the
figure;
and transfer these lines
to the
remaining
three
quarters;
and a
series of
tangents will
be obtained,
within
which
the
ellipse
can
be
drawn
by band.
5.
Constructions
by means of
two Circles.
With
the centre
of
the
Ellipse as
a
centre describe two circles
passing
through the
ends of the transverse and conjugate
axes
respectively;
draw
a
number of diameters through two opposite
quadrants;
where these diameters cut the smaller circle,
draw
parallels
to the longitudinal axis;
and where
they cut the
greater
circle, parallels
to
the transverse axis (or
vice versa);
the
points
of the
parallels will then be points on the
ellipse.
The other
points
required may
be
obtained by
producing
the
parallels
into
the remaining
quadi-ants. This construction may
be
specially re-
commended
for practical use.
6.
Practical
construction on a
larger
scale
(centres, garden-beds, &c.).
Mark
the two
foci
by nails, posts,
&c.;
place
round them a
cord equal in
length to
the transverse axis plus the
distance
between
the foci,
and tied at
both ends; stretch the
cord tense,
by means
of
a
pencil,
and let the latter run
round the foci: the
resulting figure
will
be an Ellipse.
7—12
Several
constructions
for Ellipsoids.
In constructions
7—9
the length
of
the
transverse axis has
a
definite, invariable
proportion
to
that
of
the conjugate
axis, so
that
when
the
one is given the
other
immediately
follows. In
constructions
10—12
the
length
of
each axis is
variable. The
point of junction
of
two
circles of different diameter
must lie
on
Ihe same strai*;ht
line as the centres of the two
circles.
7.
Describe two
circles each of which passes through the centre of
the
other.
Join the centres
with
the points of intersection of
the
circles:
the straight lines
so
formed
will
mark-off the four arcs
of
which,
as the figure shows, the Ellipsoid is
composed. The centre
points are marked
by small dots.
8.
Describe
two circles touching each other, and with
the point of
contact as centre, describe
a
third circle
of the same diameter.
These
three
circles cut each other in four
points.
Join
these
to
the external
centres as shown
on the figure; and the resulting
four straight
lines will again mark-off the four arcs
which are
then
to
be described
from the points indicated by the small dots.
9.
Construct two
squares, having
one
side in common, and
in them
describe
the four diagonals;
these
will then mark-off the four arcs
which
must
then be drawn from the points denoted by
small
dots.
10.
Construct
a rectangle with
sides
equal
to
the transverse
and
longitudinal
axes respectively; draw the two
transversals (the
transverse
and longitudinal axes) and join their ends in one
of
the quarters.
Cut-off
fi-om this
line, beginning from the point
of
junction
with
the
conjugate axis,
the
difference of half the
trans-
verse and half
the conjugate axis;
on
the centre point of the re-
maining
piece draw
a
perpendicular and the three
more similar
lines;
these four
lines will then show the limits
of the arcs which
are then
to
be drawn from
the points
marked by
small
dots.

The
Ellipse,
&ic.
—
The
three-centred
Arch.
33
It.
Construct
an
Oblong with sides equal
to the
transverse
and
longitudinal axes
respectively, and draw
the
two
transversals.
Measure the
half of the
transverse
axis upon half the longitudinal
axis,
and ascertain the
difference; halve
this
difference.
This half
difference must
now be taken four times along the transverse
axis
trom the centre
point of the Ellipsoid, and three times
along
the
longitudinal
axis. The four required points will
thus
be
ob-
tained.
The straight lines connecting them
will give
the oointa
of
junction
of the arcs.
12. Construction from eight centres.
Construct an
Oblong whose sides are eqtial
to
the
major and
minor axes respectively;
draw
the transversals, and join
their ends
in one of the
quarters. From the
nearest angle,
diaw a
perpen-
dicular
to
this diagonal; the points where this
perpendicular cuts
the
two axes
will
be two of the required centres.
Two more
are
obtained by
symmetrical transference. From
these
four
points
describe circles with a
radius
=
'/j
(CB-DA); the
points
where
they cut each
other internally will give four more centres.
If the
centres thus found be joined by
means
of straight
lines, as
shown
on the
figure,
the latter
will mark
the points
where the
eight
arcs
will
meet.
13
—
14.
Construction
of Ovals or egg-shaped figures. The construction
of
such figures usually
consists
in
combining
a semi-circle
with a
semi-eUipse.
13. Draw in
a
circle
two
diameters
at
right angles to each other,
and two
intersecting chords of a
quadrant; these when produced
wiU determine
the
points
where the
various arcs
meet.
The
centres of
these latter lie on
the ends of the
diameters.
14.
The
construction
of the lower
half is the same as in fig. 7.
The
centre of
the
upper lies
in the
intersection of tangents to the
lower
and upper
circles.
15.
Example of
the subdivision
and
decoration of an
ellipse,
(Storck'a
Zeichenvorlagen).
The
Three
-CENTRED Arch.
Tlie
Three-centred
arch, which was often
used
ia
the
Transition
period
between
the
Gothic
and
the Renascence, may be considered
as
a
semi-ellipsoid;
and
it
may
be described by one of the methods shown
on Plate 20
(see
also
the Head-piece
to
this Section,
on page
3).
s^-.^
mm
Meyer,
Handbook
of OraameDt.

84
B.
NATURAL FORMS.
a. The Organisms
of
Plants (Flora
of
Ornament).
In
nearly
every
style the
plant-world has been
used in
patterns.
Leaves, sprays, flowers, and
fruits,
either
singly or
combined,
have
been
adapted in ornament. The
direct
imitation of
nature,
retaining
form
and color as much
as possible, leads
to
the
naturalistic
con-
ception;
the construction of
an ornament
according
to
the rules
of
rhythm and symmetry,
with
a stricter observance
of
regularity
—
is
known as
the artificial
method.
The selection of the
comparatively few
plants from
the
luxuriant
field
of the plant-world
was partly
determined
by
beauty of
form (the
outline
of the leaf, the
delicacy
of the spray,
&c.)
and partly by
the
fact that they
possess
(or did
at some time
possess) a
symbolic
meaning.
The plates which illustrate
this section will first
exhibit the
Akanthos;
and then such plant-forms
as
are less used
or
only found
in certain styles. They
will
first
be presented
as
they
exist
in Nature;
and then
as they
were modified
in the various styles.
The Akanthos
Leaf.
(Plates 21—23.)
Of
all the ornamental
designs
which
have been borrowed from
plants; the Akanthos
is
the
most popular.
Since its
introduction
by
the
Greeks, it
recurs again
and
again
in every Western style. A
symbolical significance
has
never
attached
to the Akanthos; its
frequent

The
Akitnthos
Leaf,
ici.
35
and
varied
application is due
to the ornamental
possibilities
and
beautiful
serration
of
its leaves.
It
grows vald in
the South
of
Europe,
but
in
more
northern latitudes
is only
found in our
botanical
gardens.
There are
many varieties of the plant, of
which
we may
mention
the
following: Akanthos mollis,
with broad,
blunt tips
to
the
leaves;
Akanthos spinosus,
with pointed
lobes
terminating
in
spines,
and
comparatively narrow leaves. The conception
and
treat-
ment of
the
margin and
shape of the
leaf,
is the principal
characteristio
of
the
different
styles. The Greek
foliage has pointed leaf-edges;
in
the
Roman
style,
the tips of the leaves become
rounder, broader,
to
some
extent
with more vigorous
curves; the Byzantine and
Roma-
nesque
styles,
again, return to stiffer,
less delicate forms. The
Gothio
style,
which
used
the foreign Akanthos in
addition
to a number
of
native
plants,
adopted
in
the early
period,
round, bulbous forms; later
Gothic,
0"
the
contrary,
prefen-ed
bizarre,
long-extended, thistle-like
foliage:
in both cases
the general conception
is
more or less
naturalistic,
but
the
details
are
usually idealised
beyond
recognition. The
Renascence,
which
revived
Antique ornament,
developed the Akanthos,
and
parti-
cularly
the
Tendril, to the highest degree of perfection; in the
follow-
ing styles
formalism
degenerates in
this direction.
Modem
ornamental
art seeks
its models
in
almost
every style; and its creations
have
generally no
pronounced,
specifically
Modem
character.
Plate 21.
The
Akanthos,
and Artificial
Leaf.
1.
Leaf of Akanthos Mollis, (Jacobsthal).
2. Akanthos calyx, the leaves
and
flower of
Akanthos
Mollis,
natura-
listically
treated,
(Jacobsthal).
3. Leaf
of
Akanthos Mollis,
(Raguenet).
4. Leaf of
Akanthos
Spinosus, (Gewerbehalle).
5.
Cup,
corona of a Greek Stele,
(Raguenet).
6.
Overlap of
leaf, Roman candelabrum,
Vatican.
7. Greek
leaf, displayed, (Jacobsthal).
8. Roman
leaf. Capital
of a column, Pantheon,
Rome,
the spoon-
like roundings
of the
points of the leaves,
as
well
as the
deep
incisions,
are characteristic; and designed
to
look
well at
a distance,
Plate
22. The Artificial
Leaf.
1.
Leaf,
Roman
capital, (Raguenet).
2. Leaf
displayed,
as it
is often used on Roman
reliefs,
e.
g.:
so-
mewhat
more
richly developed,
on
the
so
called
Florentine Pilaster,
Uffizi, Florence, (Jacobsthal).
3. Byzantine
leaf,
Sta.
Sofia, Constantinople, (Raguenet).
4.
Romanesque
leaf,
St. Denis, (Li6vre).

36
NATURAL FORMS.
Plate 21.
The
Akanthos
Leaf, and
the
Artificial
Leaf.

NATURAL
FORMS.
37
The
Artificial Leaf. Plate
22.
38
NATURAL
FORMS.
Plate 23.
The
Artificial
Leaf.

The
Artificial
Leaf.
—
Artificial Foliage.
39
5.
Romanesque
leaf,
monastery
of
St.
Trophimus,
Aries, XIL centiiry
(Raguenet).
6.
Gothic
leaf, (Lifevre).
Plate 23. The
Aetificial
Leaf.
1.
Leaf,
French
Renascence, St.
Eustache, Paris.
2.
Leaf,
style
of Louis
XYI,
(Raguenet).
3.
Leaf,
French
Renascence,
church,
Epornay, (Lifevre).
4. Leaf, French
Renascence,
(Gropius).
5.
Modern Leaf,
Louvre, Paris,
(P. A.
M.
Cours d'omement).
6. Modern
Leaf,
Theatre, Monte
Carlo,
Monaco, (Raguenet).
Artificial
Foliage. (Plates
24
—
26.)
The
Scroll is
a
purely
artistic
invention,
the
natural plant having
no
tendrils.
Flowers
and calices,
such as
frequently occur in
artificial
foliage,
are
usually
developed
with serrated
edges,
composed to
recall
natural
models,
(Comp.
Plate
25,
figs. 2
und
3).
Artificial foliage is
often combined
with
forms
from plants, e.
g.:
laurel, oak, ivy,
ears
of wheat, &c.,
(Comp.
Plate
26,
figs.
2
and
4).
What was said above
of
the
Aianthos
leaf,
holds
good here too,
for' the
differences of exe-
cution
in the
various
styles.
The greatest
luxuriance
and the highest
elegance
were
attained by
the
Italian
Renascence, (Comp.
Plate
25,
fig.
5).
It is
characteristic
of
the
Louis
XVI. epoch
that the
lines
which
form
the scroU
are
somestimes
flattened,
and,
so to
speak,
make
elliptic
spirals,
(Comp.
Plate
26,
fig.
4).
Plate
24.
Artificl^l
Foliage.
1.
Ornament,
summit
of
the monument
of
Lysikrates,
Athens.
2.
Cup,
Roman.
8.
Roman
ornament,
the
so
called
"Medicean
Pilaster",
(Artificial
fo-
liage
of
a
large
size).
4.
Fragment
of a
Greek
relief, (F. A.
M.,
Cours
d'omement).
Plate
25.
Artificial
Foliage.
1.
Roman
ornament,
marble Biga,
from
the 'style
of
the
ornament
it
must
have been
an
imitation
of an
original in
bronze.
2.
Roman
ornament,
from the so
called
"Florentine
Pilaster",
a
richly
decorated
marble
relief
in the
Uffizi, Florence,
(Jacobsthal).
8.
Romanesque
frieze, St.
Denis,
(Lifevre).
4.
Early Gothic,
Notre
Dame,
Paris,
(Li^vre).
6. Renascence
ornament,
relief
on
the tomb
of
Hieronimo
Basso,
Sta.
Maria del
Popolo,
Rome, by
Sansovino,
(Gropius).

40
NATUEAL
FORMS.
Plate
24.
Aftificiul
Foliage.
