Meyer Franz. A Handbook of Ornament

Подождите немного. Документ загружается.

The Oblong, and

its

Subdivision.

—

The

Subdivision

the

Rhombus, ic. 2i

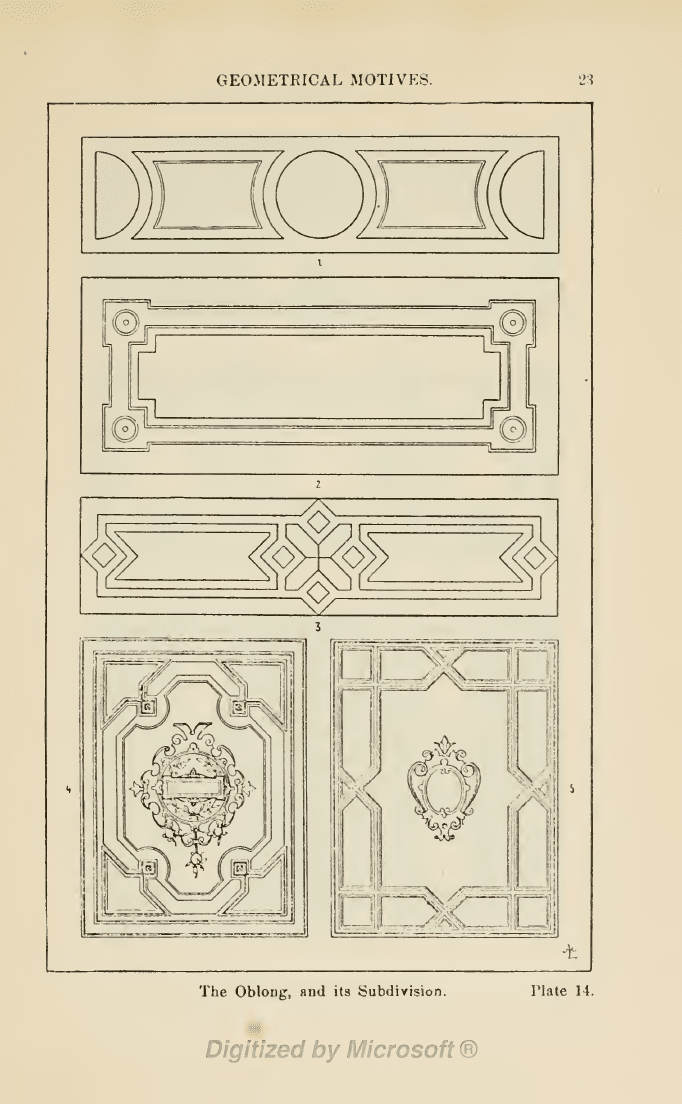
Plate 14. The Oblong.

Subdivision

for

Door panels,

Sofits

of arches,

Ac.

„ „

tablets,

&c.

„ „

Borders for ceilings.

and

Modern Album

-covers, (Gewerbehalle).

Plate

15.

The Oblong.

Ceiling, Quedlinburg,

German,

1560,

(Gewerbehalle).

Ceiling,

Massimi

Palace,

Rome, by Baldassare Peruzzi,

(Leta-

rouilly).

CofFer ceiling, Famese

Palace,

Rome, by

Barozzi

da Vignola.

(Letarouilly).

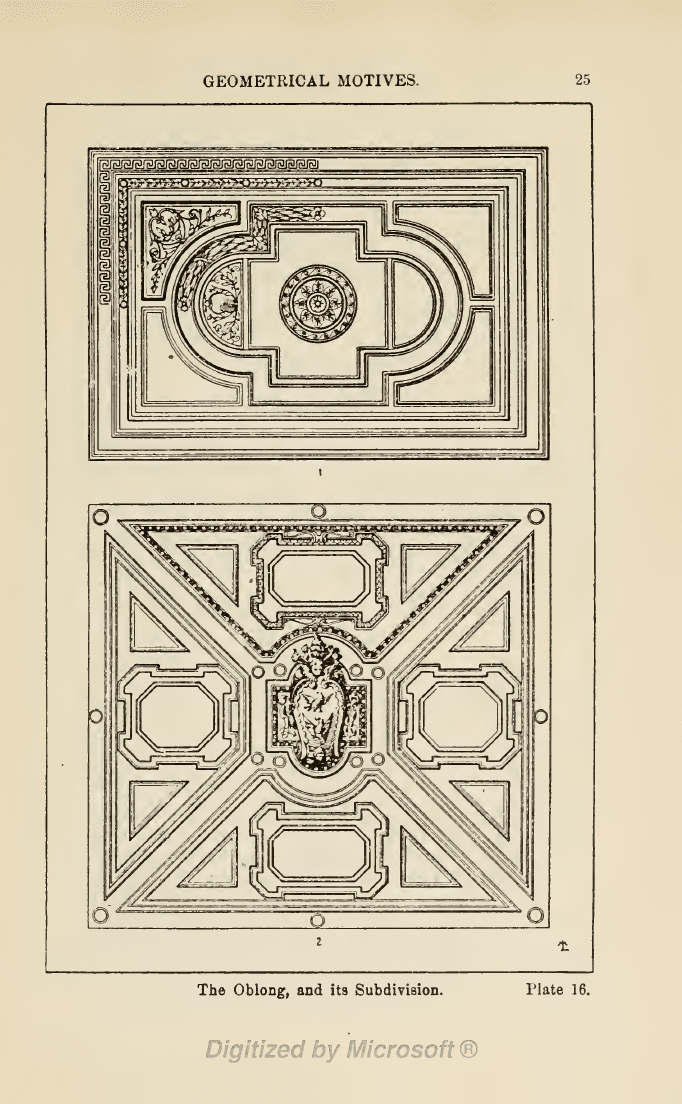
Plate 16. The Oblong.

Ceiling, modern,

(Gewerbehalle).

Vaulted

ceiling,

S. Peter's,

Rome, beginning of

the

17th

century,

(Italienisches

Skizzenbuch).

The

Subdivision of the

Rhombus,

and the

Trapezium

(Plate

17.)

Rhombus

"Lozenge"

the name

usually given to

the equi-

lateral

foursided

figure with

pairs of unequal

angles.

The

principal

auxiliary

lines

of these

figures

are the

diagonals. The

subdivision

generally

leaves

an oblong or

hexagonal panel

in the centre.

The

Trapezium

four-sided figure

with unequal sides.

The

Parallel

Trapezium

has two

parallel

sides

which

are unequal and two

equal sides

which

are not

parallel (PI.

17,

figs.

8).

The

Sym-

metrical

Trapezium has

two pairs of

adjacent

equal sides (PI.

17,

figs. 9

and

10).

Any other

irregular

four-sided rectilinear

figure

Trapezoid.

Some

suitable

subdivisions are given on

Plate

17.

Definite

directions for the

Trapezoid can scarcely

be given;

its

sub-

division

seldom easy, and varies

with each

particular case.

The

general

principle

is:

—Endeavour to

cut-off projecting

angles by

means

triangles

in such

way as

leave a

portion of the

entire

figure

regular

symmetrical. This is, however, a

matter of

artistic

taste:

and

easily learnt than taught.

Among

other applications of the

symmetrical

parallel

Tra-

pezium is

that to Cupolas of Domes:

the lines

are

indeed

curves

on a

bent

surface;

but

this causes

very little

alteration

the

sub-

division.

GEOMETRICAL

MOTIVES.

—

GEOMETRICAL

MOTIVES.

V%i

IP.

M€

C^ul

^.,<?

[i^

ja.

The Obloug,

and its

Subdivision. Plate

14.

GEOMETRICAL

MOTIVES.

Plate 15.

The Oblong,

and its Subdivision.

GEOMETRICAL

MOTIVES.

The Oblong, and its Subdivision.

Plate 16.

GEOMETRICAL

MOTIVES.

Plate

17. The

Rhombus,

the Trapezium, and their

Subdivision.

Tliff'Subdivisions

of the

Uhombvis,

&c.

—

TlioCirclc,

SiC.

—

GotliicTracciy.

Pi^TE 17.

TiiE RnoMcus, and

the TuvPEZiuii.

—

Subdivision

the Kborabus.

—

„ „

„

Parallel

Trapezium.

—

10.

„ „

Syruiuetrical

Trapezium.

The

Circle,

its Subdivision,

and

Intersections.

(Plate

18.)

The

Circle is often

used

ornamentation as

a fundamental

form.

good result

produced (as

rule)

by dividing

it merely

radii or

other

straight

lines;

and

it is therefore usually

divided

means of cui-ved lines

or of a combination

of arcs and

straight

lines.

describing circles

to cut each

otlier: motives may

obtained,

shown by figures

and

the

latter of

which

is the

basis

of a

Roman

mosaic

pavement

found

in Pompeii (Figure

17).

That

circles which

cut

each -other form of

themselves

efifec-

tive pattern

—

is shown

by the

engine-tm-ned

ornament, which

is pro-

duced by

machinery

and applied

to the

decoration

Watch-cases,

and to the

plates from

which

Bank

notes,

certificates,

&c.

arc

printed.

Ornamentation

means of arcs plays

a conspicuous

part in

Gothic tracery,

which

will

treated-of in the

following

chapter.

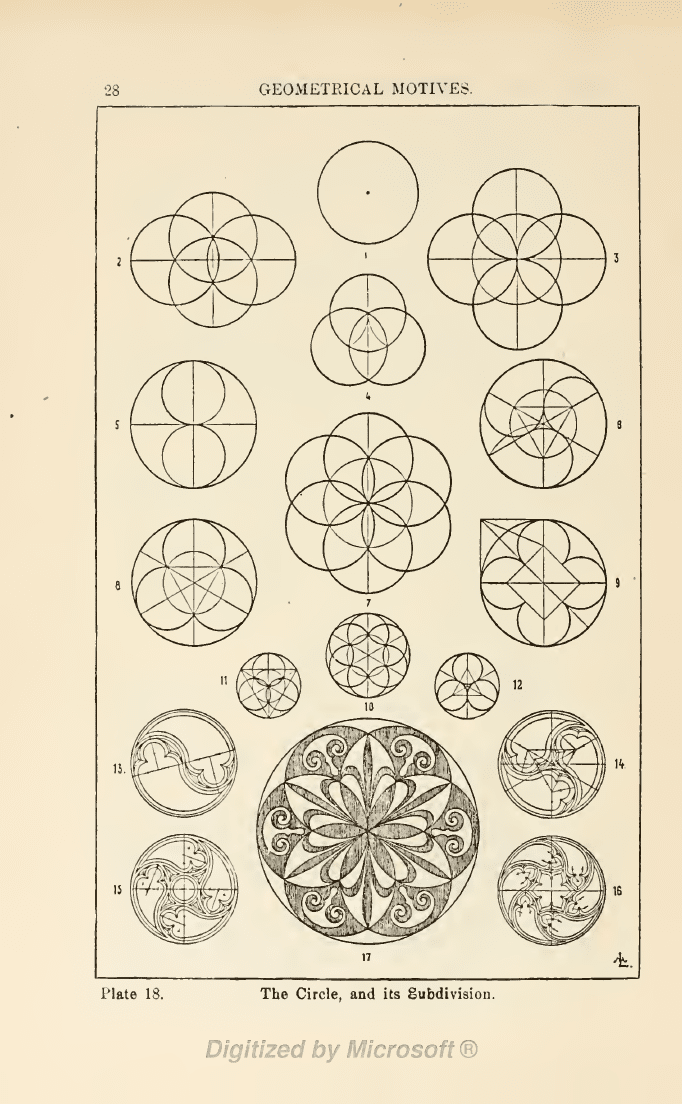
Plate

18. The

Circle.

—

12.

Different

divisions

and

intersections.

—

IG.

Tracery

in the

Gothic

style.

17. Centre

mosaic

pavament,

Pompeii, (Kunsthandwork).

Gothic

TracEry.

(Plato

19.)

In the

forms of

Tracery,

the Gothic style evolved

and

brought

perfection

a characteristic

decoration

means

of arcs of

circles.

And although

the

results

have

something stiff and mechanical,

when

compared

-with the

ornaments

taken

direct from nature in other

styles,

cannot

be denied

that

they

possess a

great originality, and

richness

of form.

Tracery

was

chiefly

applied

stone, and wood;

architecture,

and

furniture;

for

galleries,

windows,

and

panels,

&c.

Well-known

forms

are the

circles

(figs.

—16

of Plate

showing

2, 3,

and

6 foliations),

the trefoil (Plate

19,

figs.

3 and

4),

GEOxMETRICAL

MOTIVES

Plate

18. The Circle,

and its Sufadivisiou.

GEOMETRICAL

MOTIVES.

Gothic Tracery.

I'late 19.

30 Gothic

Tracery.

—

The

Ellipse.

the

quatrefoil

(in the

centre of fig.

2),

the cinquefoil,

&c.

The pro

jecting

points

are termed cusps,

the voids between

the

cusps aro

termed foils.

Plate 19.

Tracery.

—

11. Gothic

tracery,

for

panels and windows.

The figures

give

partly

the

fundamental construction,

partly the fmiher

deve-

lopement.

Thus

figures

and

3 and

6 and

8 and

10 and

11,

belong together.

The

Ellipse.

(Plate

20.)

The

Ellipse

is a figure,

whose radius of

curvation

is continually

changing.

It has the peculiar

quality that,

any point

on the

circumference

joined

with the

two foci,

the

sum of the two

con-

necting lines

invariable,

and

always equal to the longitudinal axis.

The three-centred arch is an

approximate construction

to an

elliptic curve.

is composed of a

number of

arcs,

which

not

possible in the

case

of the ellipse. As

regards beauty

line it

can

never be a substitute for the Ellipse; but its

easier construction has,

notwithstanding, caused it

used for

many purposes.

The expression "Oval" for the

ellipse, is erroneous. Oval is

derived from "ovum"

(egg),

and therefore

means

egg-shape.

The Ellipse

of comparatively late

appearance

art,

the

con-

struction presupposing

certain

knowledge of

Geometry, which was

not

possessed

primitive peoples.

Afterwards it

became of common

application,

will

seen from many

passages

of this Handbook.

The

Ellipse

is a

very popular shape

for ceilings,

panels, boxes, and

dishes.

Figui-e

affords hints as

the

manner of

subdividing

it.

PiJVTE 20.

The Ellip.se, <fcc.

—

2. Construction by

means of 8 points.

When

the

square with

its

diagonals and

transversals is

projec-

ted as an Oblong,

the circle

described in it

becomes

an Ellipse.

Construction from the

Foci.

From the

ends of the

conjugate

axis,

doficribe

circles

with

radius of one

half

the

transverse

axis;

the

points

where these

circles cut

each other

will

the

foci.

Now

divide the

trans-

verse axis into

two unequal

parts,

and from

the

foci as centres

describe

circles having these

unequal

parts

for

their

radii; the

points of

intersection

will

four

points of the

Ellipse.

Another

division will

give

another four

points,

and so

on.

Co'istruction by means of

Tangents.

Construct an Oblong

with sides of the

lengths of the

transverse

and

conjugate

axes

respectively;

draw the

transversals,

tjiat is,