Menke W. Geophysical Data Analysis: Discrete Inverse Theory
Подождите немного. Документ загружается.


208
12
Sample Inverse Problems
sphere
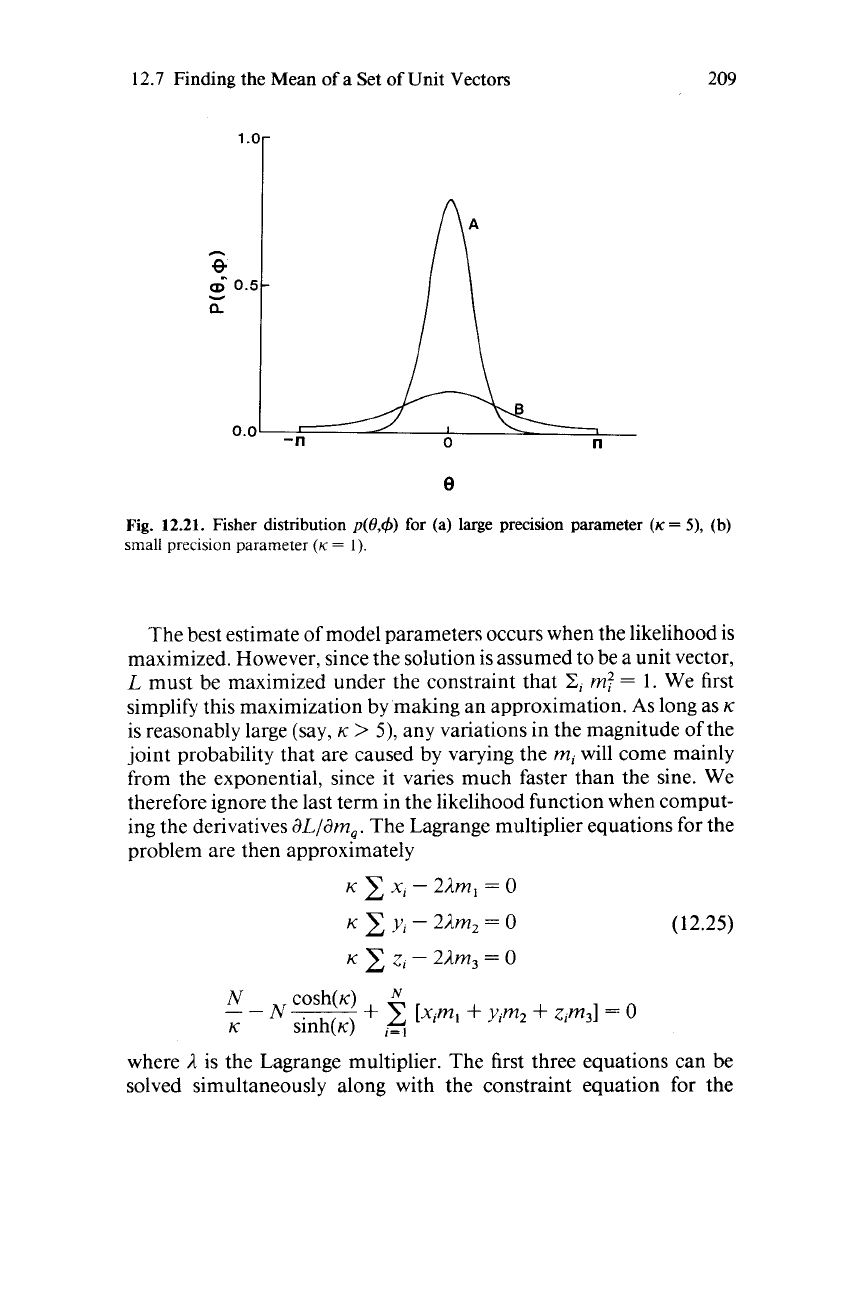
Fig.
12.20.
Coordinate system used in Fisher distribution.
This distribution is peaked near the mean direction
(8
=
0),
and its
width depends
on
the value of the
precision parameter
K
(Fig.
12.2 1).
The reciprocal of this parameter serves a role similar to the variance in
the Gaussian distribution. When
K
=
0
the distribution is completely
white
or
random on the sphere, but when
K
>>
1
it becomes very
peaked near the mean direction.
If
the data are specified by NCartesian unit vectors
(x,
,
y,,
z,)
and the
mean by its unit vector
(ml
,
m2,
m3),
then the cosine of the inclination
for any data is just the dot product cos(8,)
=
[xlml
+
y,m2
+
z~z~I.
The joint distribution for the data
P(0,
4)
is then the product of
N
distributions
of
the form
P(8,,
4,)
sin(@,). The sin(8,) term must be
included since we shall be maximizing the joint probability with
respect
to
m,
and not with respect to solid angle. Thejoint distribution
is then
N
P(0)
=
[~/4n
sinh(ic)IN exp
where cos(Oi)
=
xim,
-k
ylm,
+
zim3
and the likelihood function is
L
=
log(P)
=
N
log(K)
-
N
log(&)
-
N
log[sinh(~)]
N
N
(12.24)
12.7
Finding
the
Mean
of
a
Set
of
Unit
Vectors
209
Fig.
12.21. Fisher
distribution
p(@#~)
for (a) large precision parameter
(K
=
5),
(b)
small
precision
parameter
(K
=
I).
The best estimate of model parameters occurs when the likelihood is
maximized. However, since the solution is assumed to be a unit vector,
L
must be maximized under the constraint that
C,
rnf
=
1.
We first
simplify this maximization by making an approximation.
As
long as
K
is reasonably large (say,
K
>
5),
any variations in the magnitude of the
joint probability that are caused by varying the
rn,
will come mainly
from the exponential, since it varies much faster than the sine. We
therefore ignore the last term in the likelihood function when comput-
ing the derivatives
dL/drn,.
The Lagrange multiplier equations for the
problem are then approximately
K
x
XI
-
2h,
=
0
K
x
y,
-
Urn,
=
0
K
z,
-
2h3
=
0
(1
2.25)
N
cosh(ic)
-
-
N7
+
K
sinh(ic)
[xirn,
+
yirn,
+
zirn3]
=
0
where
A
is the Lagrange multiplier. The first three equations can be
solved simultaneously along with the constraint equation for the

2
10
12
Sample Inverse Problems
X
Fig.
12.22.
Maximum likelihood estimate
of
the Fisher distribution’s central vector
(bold)
is
parallel
to
the vector
sum
of
the data.
model parameters as
(12.26)
and the fourth equation is then an implicit transcendental equation for
K.
Since we have assumed that
K
>
5,
we can use the approximation
cosh(lc)/sinh(lc)
=
1,
and the fourth equation yields
K
=
N/[N
-
z
cos(8,)].
The mean vector is the normalized vector sum of the individual
observed unit vectors (Fig.
12.22).
12.8
Gaussian Curve Fitting
Many types
of
spectral data consist of several overlapping peaks,
each
of
which has a Gaussian shape (Fig.
12.23).
The problem is to
determine the location, area, and width of each peak through least
squares curve-fitting.
Suppose that the data consist of
N
(z,
d)
pairs, where the auxiliary
variable
z
represents spectral frequency. Each
of,
say,
q
peaks is

12.8
Gaussian
Curve
Fitting
21
1
frequency
Fig.
12.23.
Hypothetical x-ray fluorescence data containing two spectral peaks.
parameterized by its center frequencyf;, area
Ai,
and width
ai.
There
are then
M
=
3q
model parameters
mT
=
[
fi
,
A
,
,
a,
,
.
. .
,f,,
A,,
aq].
The model is nonlinear and of the form
d
=
g(m):
(1
2.27)
If
the data have Gaussian error, it is appropriate to use an iterative
L,
method to solve this problem. Furthermore, this problem will typically
be overdetermined, at least if
N
>
M
and if the peaks do not overlap
completely. The equation is linearized around an initial guess using
Taylor's theorem, as in Section
9.3.
This linearization involves com-
puting the derivatives
Vg.
In this problem the model is simple enough
for the derivatives to be computed analytically as
ag,/aA,
=
[
~/Go,I
exp[-(z,
-J)~/~o,ZI
%/aJ
=
[A,/GO,21[((Z1
-J)2/Of)
-
11
exP[-(Z,
-J)*/241
dg,
/do,
=
[A,
/&a,]
KZ,
-
J)/~,zI
exp[--
(z,
-
J)~/~o,zI
(12.28)
These derivatives are evaluated at an initial guess
Gt
based on visual
inspection of the data. Improved estimates of the model parameters
are found using the recursions
Vg,AmFi,
=
d
-
g(myt)
and
m",":,
=
myf
+
Am,,,
,
where the matrix equation can be solved with the
simple least squares method. The iterations are terminated when the
correction factor
Am,,
,
becomes negligibly small (for instance, when
the absolute value of each component becomes less than some given
tolerance).
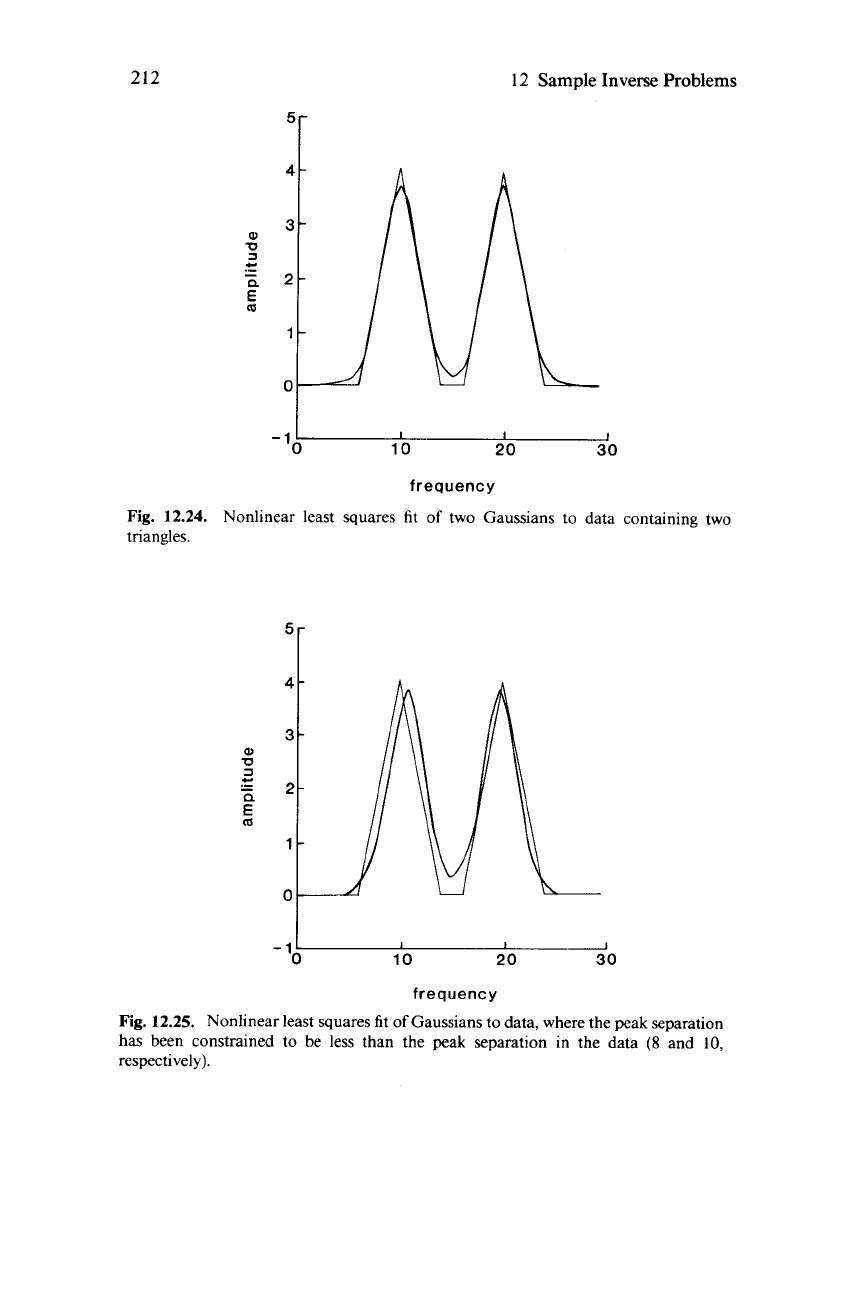
To
illustrate the procedure, we fit Gaussian curves to
30
synthetic
data
containing two triangular peaks (Fig.
12.24).
The iterative
method converges in
7
iterations.
Occasionally there is a priori information that separation between
212
12
Sample
Inverse
Problems
I
1
I
10
20
30
frequency
Fig.
12.24.
Nonlinear least squares fit
of
two Gaussians to data containing two
triangles.
1
,
I
10
20
30
frequency
Fig.
12.25.
Nonlinear least squares fit
of
Gaussians to data, where the peak separation
has been constrained to
be
less than the peak separation in the data
(8
and
10,
respectively).

12.9
Earthquake
Location
213
two peaks must equal a gven constantf;
-4
=
(sjj).
This constraint
can be implemented by imposing it at each iteration;
F
Amy:,”:,
=
h,
where
(12.29)
These constraints can be implemented either by Lagrange multipliers
or by Householder transformations. An example computed by the
latter method
is
shown in Fig. 12.25. The peak separation is con-
strained to be somewhat larger than the peak separation in the data,
so
the fit is not particularly good. This calculation also converges in seven
iterations.
One of the drawbacks to these iterative methods is that if the initial
guess is too far
off,
the solution may oscillate wildly or diverge from
one iteration to the next. There are several possible remedies for this
difficulty. One is to force the perturbation
Amn+
I
to be less than a given
length. This result can be achieved by examining the perturbation on
each iteration and, if it is longer than some empirically derived limit,
decreasing its length (but not changng its direction). This procedure
will prevent the method from wildly “overshooting” the true mini-
mum but will also slow the convergence. Another possibility is to
constrain some of the model parameters to equal a priori values for the
first few iterations, thus allowing only some of the model parameters to
vary. The constraints are relaxed after convergence, and the iteration is
continued until the unconstrained solution converges.
12.9
Earthquake
Location
When a fault ruptures within the earth, seismic compressional Pand
shear
S
waves are emitted. These waves propagate through the earth
and can be recorded by instruments on the earth’s surface. The
earthquake location problem is to determine the location
(xo,
yo,
zo)
and time
to
of the rupture on the basis
of
measurements of the time of
amval of the waves at the instruments.
The forward problem- that of predicting the travel time of seismic
waves given a particular source (fault), receiver geometry, and seismic
velocity structure in the earth-is quite formidable. We shall not
discuss it here, but note that it usually requires finding the path, or
ray,

214
12
Sample Inverse Problems
Fig. 12.26.
Compressional
P
and shear
S
waves travel along rays
from
earthquake
source
S
to receiver
R.
The ray path is determined by the position
of
source and receiver
and the velocity structure
of
the medium.
that the waves followed as they traveled from source to receiver (Fig.
12.26). The process of
ray
tracing
is a lengthy numerical task typically
performed with a computer.
Assuming that the travel time
T,(m)
=
T(m,
x,,
y,,
z,)
of a
P
and
S
wave from an earthquake at
mT
=
(xo,
yo,
zo,
to)
to a receiver at
(x,
,
y,,
z,)
can be calculated, the model can then be written as
tP,
=
TP(m,
4,
Y,,
z,)
+
to
ts,
=
Ts(m,
x,,
Y,,
z,)
+
to
(12.30)
where
t,
is the amval time of the given wave at the ith receiver. These
equations are nonlinear and of the form
d
=
g(m).
If
many observa-
tions are made
so
that the equations are overdetermined, an iterative
least squares approach may be tried. This method requires that the
derivatives
OT,
be computed for various locations of the earthquake.
Unfortunately, there is no simple, differentiable analytic formula for
travel time. One possible solution is to calculate this derivative nu-
merically using the finite difference formula
-_
aT,
-
[T,(m
+
[E,
0, 0,
0lT)
-
T,(m)l
--
dT,
-
[T,(m
+
[O,
E,O,
OIT
-
T,(m)l
--
dT,
-
[T,(m
+
[O,
0,
E,
OIT
-
T,Wl
dm,
E
dm2
E
dm,
E
(12.31)

12.9
Earthquake
Location
215
Note that
aTJam,
=
0
since the travel time depends only on the
location of the earthquake and not on its time of occurence. These
equations represent moving the location of the earthquake a small
distance
E
along the directions of the coordinate axes and then com-
puting the change in travel time. This approach has two disadvantages.
First, if
E
is made very small
so
that the finite difference approximates a
derivative very closely, the terms in the numerator become nearly
equal and computer round-off error can become very significant.
Second, this method requires that the travel time be computed for
three additional earthquake locations and, therefore, is four times as
expensive as computing travel time alone.
In some inverse problems there is no alternative but to use finite
element derivatives. Fortunately, it is possible in this problem to
deduce the gradient of travel time by examining the geometry of a ray
as
it leaves the source (Fig.
12.27).
If
the earthquake
is
moved a small
distance
s
parallel to the ray in the direction of the receiver, then the
travel time is simply decreased by an amount
s/v(m),
where
u(m)
is the
appropriate wave velocity in the vicinity of the source.
If
it is moved a
small distance perpendicular to the ray, then the change in travel time
is negligible since the new ray path will have nearly the same length as
the old. The gradient is therefore
BT
=
s/u(m),
where
s
is a unit vector
tangent to the ray at the source that points away from the receiver.
Since we must calculate the ray path to find the travel time, no extra
computational effort is required to find the gradient.
If
sPl(rn)
is the
Fig.
12.27.
(a) Moving the source from
xo
to
XI
parallel to the ray path leads to a large
change in travel time.
(6)
Moving the source perpendicular to the ray path leads to
no
(first-order) change in travel time. The partial derivative
of
travel time with respect to
source position can therefore
be
determined with minimal extra effort.
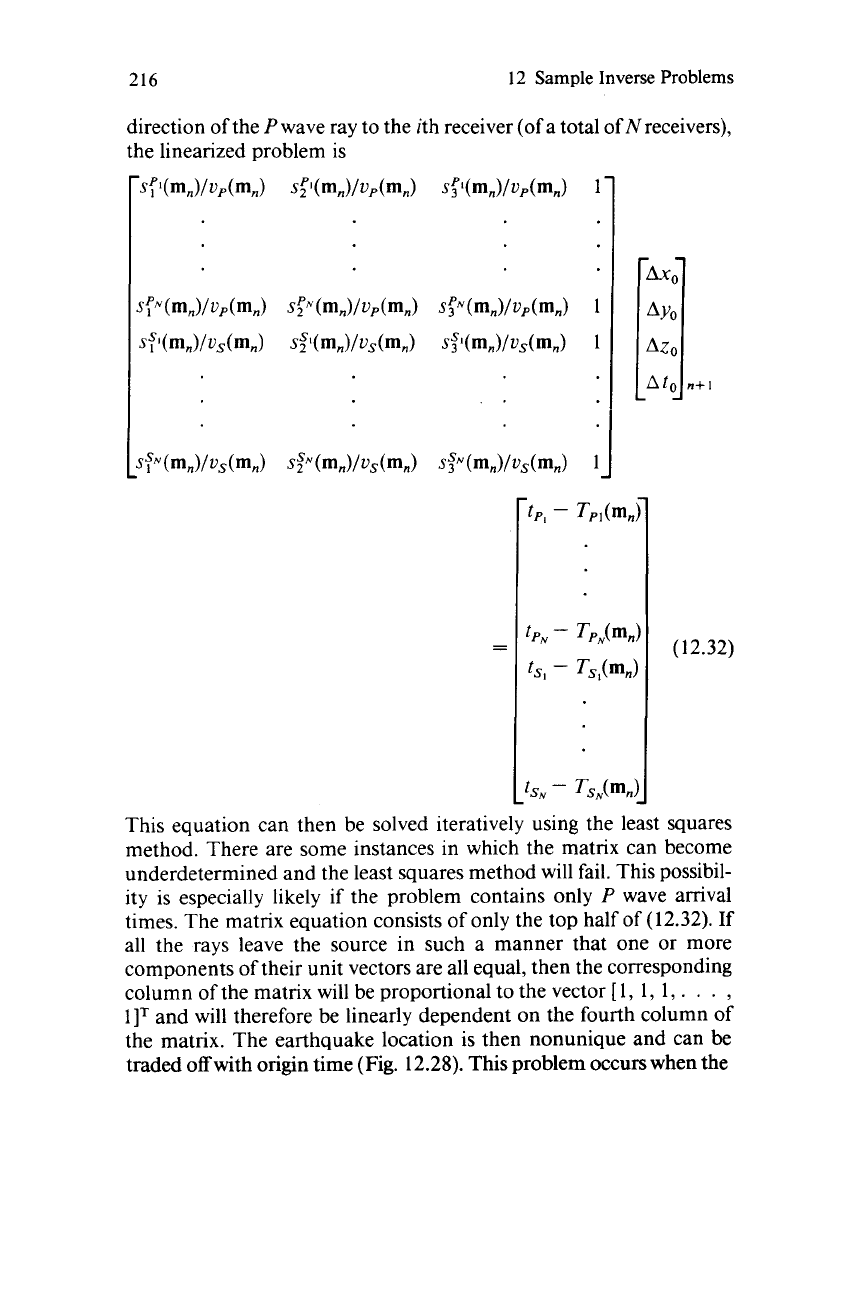
216
12
Sample Inverse Problems
direction of the
P
wave ray to the ith receiver (of a total of Nreceivers),
the linearized problem is
..
This equation can then be solved itera
kN
-
Ts,<m,>
ively using the least squa
:S
method. There are some instances in which the matrix can become
underdetermined and the least squares method will fail. This possibil-
ity
is
especially likely
if
the problem contains only
P
wave amval
times. The matrix equation consists of only the top half of
(12.32).
If
all the rays leave the source in such a manner that one or more
components of their unit vectors are all equal, then the corresponding
column of the matrix will be proportional to the vector
[
1,
1,
1,
. .
.
,
1IT
and will therefore be linearly dependent on the fourth column of
the matrix. The earthquake location is then nonunique and can
be
traded
off
with
origin time (Fig.
12.28).
This problem
occurs
when the

12.10
Vibrational
Problems
217
\
(b)
Fig.
12.28.
(a) In layered media, rays follow “refracted” paths, such that rays to all
receivers (triangles) leave the source (star) at the same angle. The position and travel
time of the source on the dashed line therefore trade
off.
(b)
This phenomenon also
occurs in nonlayered media if the earthquake is far from the receivers.
earthquake is far from all of the stations. The addition ofS wave arrival
times resolves the underdeterminacy (the columns are then propor-
tional to
[I,
1, 1,
. . .
,
1,
vs/vp,
. .
.
,
IT
and are not linearly
dependent on the fourth column). It is therefore wise to use singular-
value decomposition and the natural inverse to solve earthquake
location problems, permitting easy identification of underdetermined
cases.
The earthquake location problem can also be extended to locate the
earthquake and determine the velocity structure of the medium simul-
taneously. It then becomes similar to the tomography problem (Sec-
tion
12.4)
except that the orientations of the ray paths are unknown.
To ensure that the medium is crossed by a sufficient number
of
rays to
resolve the velocity structure, one must locate simultaneously a large
set of earthquakes-on the order of
100
[Ref.
51.
12.10
Vibrational
Problems
There are many inverse problems that involve determining the
structure of an object from measurements of its characteristic fre-
quencies of vibration (eigenfrequencies). For instance, the solar and
terrestrial vibrational frequencies can be inverted for the density and
elastic structure of those two bodies. These inverse problems are
typically nonlinear. Special effort must therefore be made to find
simple means of calculating the partial derivatives
of
eigenfrequency
with respect to the structure. We shall describe a general procedure for
calculating these derivatives that is based on perturbation theory and
that is applicable whenever the vibrations satisfy a linear, second-order
