Mellouk A., Chebira A. (eds.) Machine Learning

Подождите немного. Документ загружается.

Generation of Facial Expression Map using Supervised and Unsupervised Learning

253

ID An. Sa. Di. Ha. Su. Fe. Ne.

Extracted

Categories

Representative

Images

A 1 1 1 1 1 1 2 8 40 ( 5 units * 8 )

B 1 1 1 1 1 - 2 7 35 ( 5 units * 7 )

C 1 1 1 3 1 2 6 15 75 ( 5 units * 15 )

D 1 1 1 3 1 1 7 15 75 ( 5 units * 15 )

E 1 2 1 1 1 1 3 10 50 ( 5 units * 10 )

F 1 1 1 1 1 1 3 9 45 ( 5 units * 9 )

Table 2. Numbers of facial expression categories and representative images.

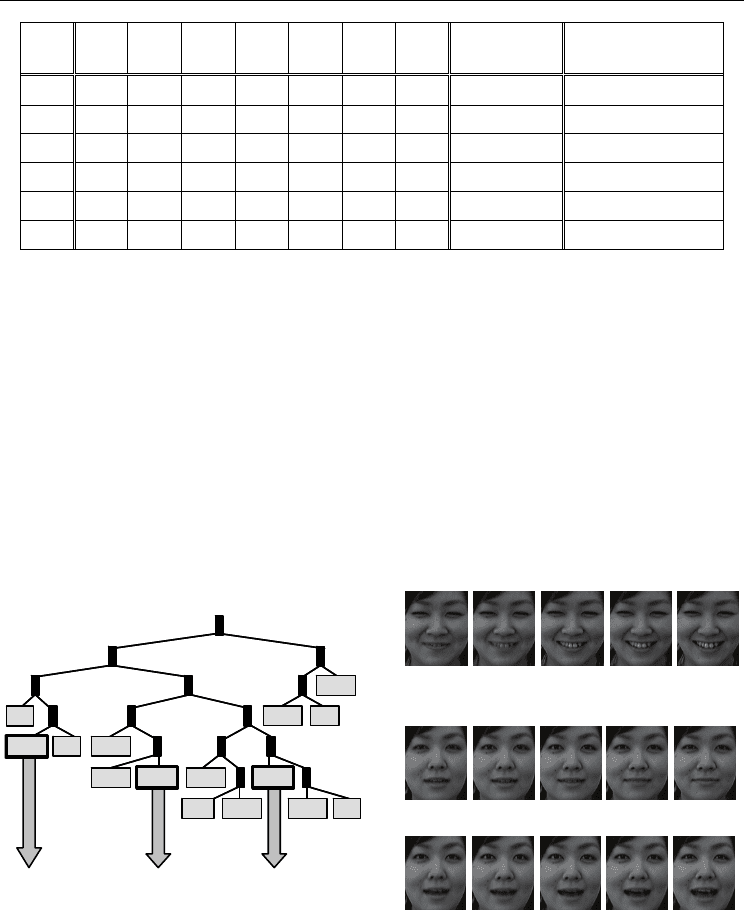
For Subject A, 8 categories are generated and 40 representative images are extracted. In fact,

Subject A presented stable facial expression patterns within training data, and his six basic

emotions were generated as one category each. A neutral expression was generated as two

categories.

On the other hand, 15 categories were generated and 75 representative images were

extracted for Subject D. Regarding happiness, three categories were generated from her one

facial expression. Figure 6 shows representative images of happiness of Subject D, which

reveals that three types of categories representing happiness were generated: (a) eyes are

closed and the mouth is opened (showing teeth), (b) smiling, and (c) mouth is opened

widely. These images suggest that the facial expression for the happiness of Subject D had

multiple facial expression patterns, which were learned as different facial expression

topological characteristics, and which were categorized into different categories in the

binary-tree structure of SOM.

(b) Smiling.

(a) Eyes are closed and mouth is opened

(showing teeth).

Ha.1 Di.

Ne.3

Sa.

Ne.2 Su.

Ne.1

Ne.4 Ha.2 Ne.5 Ha.3

An. Ne.6 Ne.7 Fe.

(a) (b) (c)

Fig. 6. Representative images of happiness of Subject D (Detail of Fig. 5(d)).

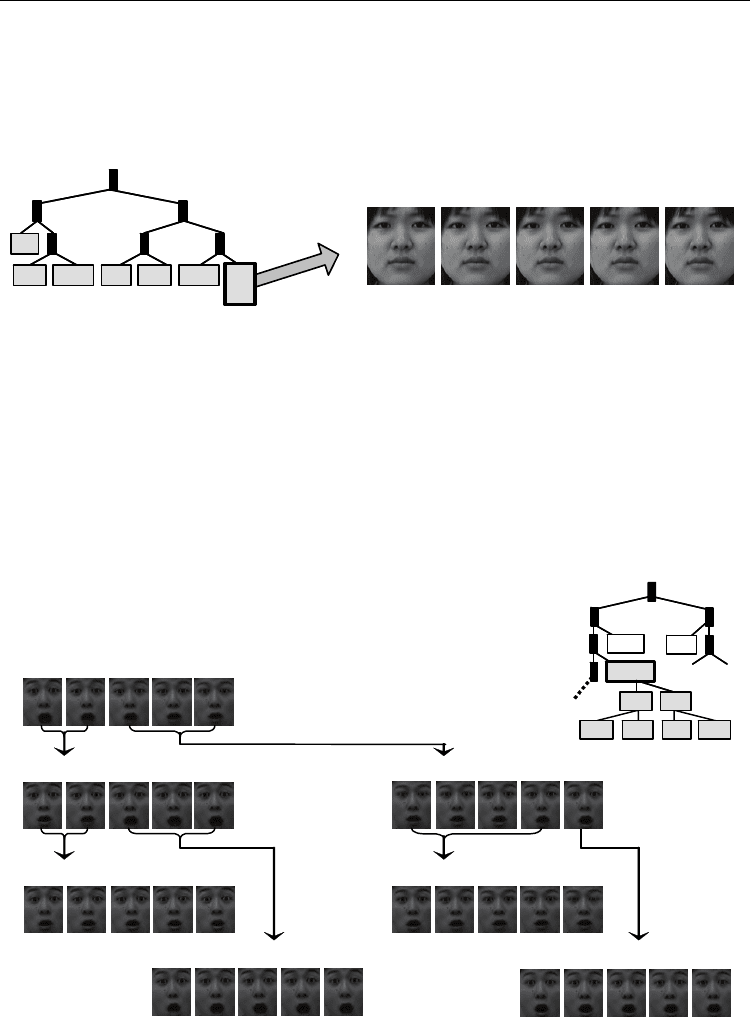
For Subject B, 7 categories were generated and 35 representative images were extracted.

Regarding disgust and fear, both were classified into a single category (Fig. 7). Comparison

of disgust and fear as facial expressions of Subject B shown in Fig. 4 suggests similarities in

the patterns of facial expression and the consequent difficulty in visual distinction between

Machine Learning

254

both, which indicates that the binary-tree structure of SOM generated the facial expression

of similar topological characteristics as one category.

The following were revealed. The proposed method enables classification of multiple facial

expression patterns into separate different categories even if they are of the same facial

expression. On the other hand, visually similar facial expressions are classifiable into one

category.

Ha. Ne.1 Su. An. Ne.2

Di.

Fe.

Sa.

Fig. 7. Representative images of “disgust” and “fear” (Subject B, Detail of Fig. 5(b)).

Psychological significance is assigned to every category obtained with the binary-tree

structure in this study. The operator might also assign importance to categories that are

selected according to personal subjectivity. Moreover, intentional further hierarchization

permits us to subdivide categories (subdivision of facial expression categorization). For

example, Fig. 8 shows the subdivision result of the surprise category related to Subject E.

The fourth layer, Fig. 8(a), was defined as a surprise category. Classification based on local

and small changes of a facial expression pattern was performed by further intentional

hierarchization: eyebrows are raised greatly (Fig. 8(b)), eyebrows are raised slightly (Fig.

8(c)), the mouth is opened narrowly (Figs. 8(d) and 8(f)), and the mouth is opened widely

(Figs. 8(e) and 8(g)).

(b) Eyebrows are raised greatly.

(a) Category defined as Surprise.

(d) Mouth are opened narrowly.

(e) Mouth is opened widely.

(f) Mouth is opened narrowly.

(g) Mouth is opened widely.

Su. (a)

Ne.1

Ha.

( b ) ( c )

( d ) ( e ) ( f ) ( g )

(d) Mouth is opened narrowly.

Fig. 8. Subdivision of a surprise category of Subject E (Detail of Fig. 5(e)).

Generation of Facial Expression Map using Supervised and Unsupervised Learning

255

5.2 Generation of facial expression map

The categories and representative images extracted in Section 5.1 were used respectively as

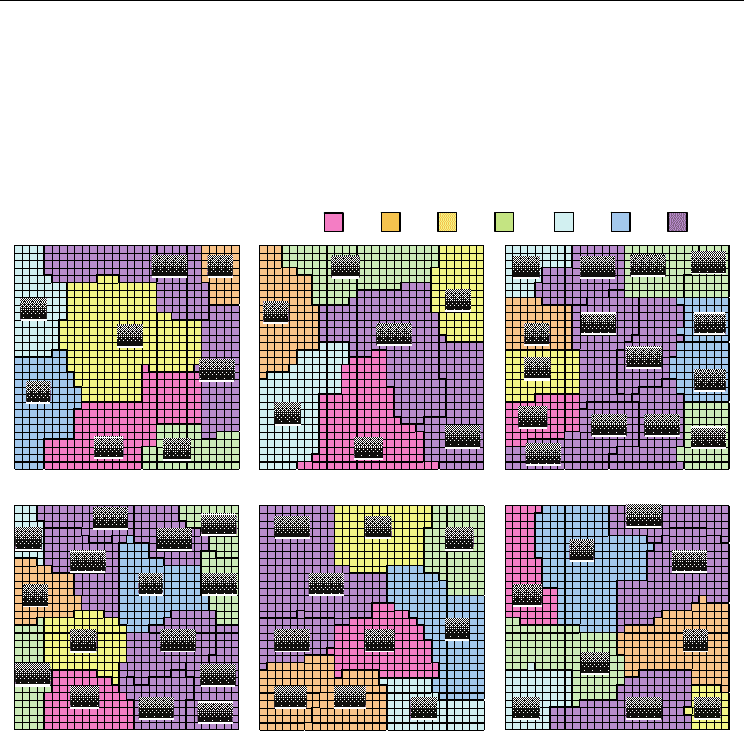
teacher signals and input data of the CPN; the FEMaps shown in Fig. 9 were generated

using the proposed method. Units with a round mark in the figures denote winner units

when training data were input into the CPN after learning. These figures suggest that the

area size of facial expression categories (number of labels) on FEMaps differs for each

subject. Even within one subject, differences are apparent in the number of labels for each

facial expression category.

○○○○○

○

○○

○ ○○

○○ ○

○

○○○

○

○○

○

○○ ○

○○

○ ○

○

○○○○○○

○ ○ ○ ○ ○

○

○ ○

○

○ ○

○

○ ○ ○

○ ○ ○ ○

○ ○ ○ ○ ○ ○ ○

○

○ ○

○ ○ ○ ○ ○

○ ○ ○

○

○ ○

○ ○ ○ ○ ○ ○

○ ○ ○ ○

○ ○

○ ○ ○

○ ○

○ ○ ○ ○ ○

○

○ ○ ○ ○

○ ○

○ ○ ○ ○ ○

○

○ ○ ○ ○ ○ ○ ○

○ ○ ○ ○ ○ ○ ○ ○ ○

○ ○

○ ○ ○ ○

○ ○

○

○ ○

○

○ ○ ○

○ ○

○ ○ ○

○

○ ○

○ ○ ○ ○

○ ○

○ ○ ○

○

○ ○ ○

○

○ ○ ○ ○

○ ○

○ ○ ○ ○ ○

○

○ ○

○ ○ ○

○

○ ○ ○ ○

○

○ ○ ○ ○

○ ○ ○

○ ○

○

○ ○

○

○ ○

○ ○ ○ ○ ○ ○ ○

○ ○

○

○ ○

○

○ ○

○ ○ ○

○

○ ○

○ ○ ○

○

○ ○ ○

○ ○

○

○ ○

○ ○ ○ ○ ○

Ne.2

Ne.1

Ha.

Sa.

Di.

Su.

Fe.

An.

Ne.1

Ne.2

An.

Ha.

Sa.

Di.

Su.

Ne.2

Ne.4

Ha.1

Ne.6

Fe.1

Ha.2

Ne.1

Ne.3

Ha.3

Fe.2

Ne.5

An.

Sa.

Di.

Su.

Ha.1

Ne.3

Ne.2

Ne.1

Ne.4

Ha.2

Ne.5

Ha.3

Ne.6

Ne.7

An.

Sa.

Di.

Su.

Fe.

Sa.1

Ne.1

Ne.2

Sa.2

Ne.3

An.

Ha.

Di.

Su.

Fe.

Ne.1

Ne.2

Ne.3

An.

Ha.

Sa.

Di.Su.

Fe.

(a) Subject A (b) Subject B

(d) Subject D (e) Subject E (f) Subject F

An.

Sa. Di. Ha. Su. Fe. Ne.

Fig. 9. FEMaps generated with the proposed method.

The percentages of the number of labels for each subject are listed in Table 3. Sadness and

disgust occupy 4.1% and 25.2%, respectively, for Subject A. Even though training data of the

same number for both categories (five images per category) are being used, great differences

are apparent in the number of labels. Figure 9(a) portrays that winner units of training data

for sadness are crowded, whereas those for disgust are dispersed widely, which are

presumed to suggest the following Regarding sadness, the topological characteristics of

training data are very similar compared to other facial expressions that the facial expression

pattern changes little. However, for disgust, differences in the topological characteristics of

training data are so large that the facial expression pattern changes greatly. For Subject D,

the facial expression of happiness, for which three categories were generated, changes

greatly (15.6%), although that of surprise shows little change (3.0%). For Subject F, the facial

expression of fear changes greatly (20.2%), whereas that of disgust shows little change

Machine Learning

256

(3.3%). These results suggest that the number of labels on an FEMap express the extent of

difference of topological characteristics within a category, i.e., expressiveness of person-

specific facial expressions.

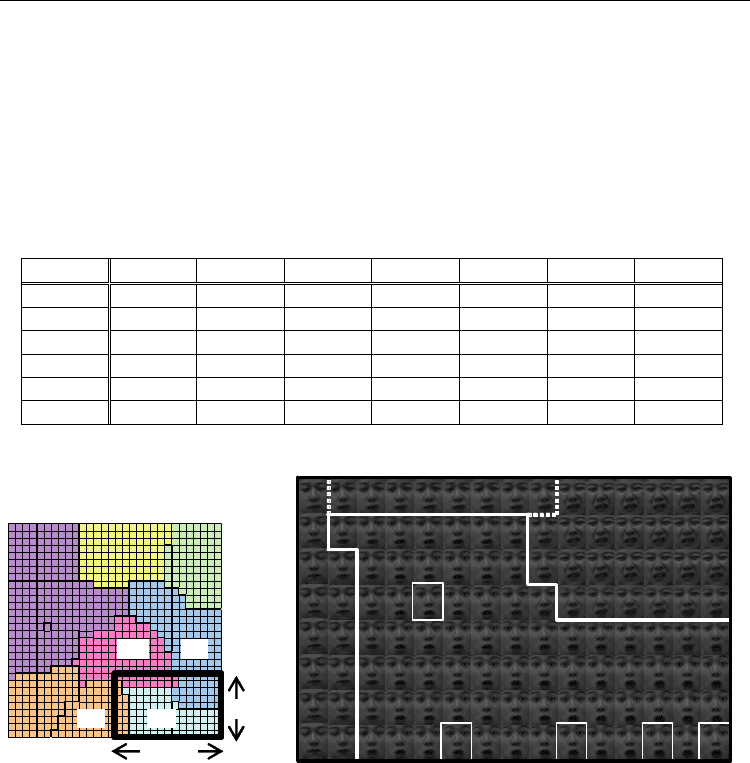
Figure 10 portrays a magnified view of a part of surprise in the FEMap of Subject E, with the

weights of each unit visualized. Units with the white frame in the figure denote winner

units when training data were input into the CPN after learning. This figure suggests that

facial expressions whose patterns differ slightly are generated in the neighborhood of five

winner units. These results suggest that data expansion is performed based on the similarity

and continuity of training data, and that more facial expression patterns such as mixed facial

expressions between categories can be generated in the CPN mapping space.

ID An.(%) Sa. (%) Di. (%) Ha. (%) Su. (%) Fe. (%) Ne. (%)

A 17.7 4.1 25.2 7.2 9.4 11.9 24.4

B 18.0 11.7 9.2 13.3 14.8 - 33.0

C 6.3 6.6 7.1 17.1 5.0 10.7 47.2

D 9.1 6.8 9.2 15.6 3.0 11.0 45.3

E 11.6 16.2 11.6 9.4 8.0 15.7 27.6

F 9.1 13.9 3.3 12.8 7.1 20.2 33.6

Table 3. Percentages of number of labels in the FEMap.

○ ○ ○ ○ ○

○

○ ○

○ ○ ○

○

○ ○ ○ ○

○

○ ○ ○ ○

○ ○ ○

○ ○

○

○ ○

○

○ ○

○ ○ ○ ○ ○ ○ ○

○ ○ ○ ○ ○

○

○ ○

○ ○ ○

○

○ ○ ○ ○

○

○ ○ ○ ○

○ ○ ○

○ ○

○

○ ○

○

○ ○

○ ○ ○ ○ ○ ○ ○

15 unit

8 unit

Su.Sa.

Fe.An.

Fig. 10. Magnified view of a part of surprise in the FEMap of Subject E (Detail of Fig. 9(e)).

6. Conclusion

On the assumption that facial expression is a problem of classification into an unknown

number of categories, this chapter describes an investigation of a generation method of a

person-specific FEMap. The essential results obtained in this study are the following.

Hierarchical use of SOM with a narrow mapping space enables extraction of person-specific

facial expression categories and representative images for each category. Psychological

significance is assigned to every category obtained with the binary-tree structure in this

study. The operator might also give special importance to categories selected according to

personal subjectivity. Moreover, intentional further hierarchization of a binary-tree structure

permits the additional subdivision of facial expression categorization.

Generation of Facial Expression Map using Supervised and Unsupervised Learning

257

The categories and category representative images obtained from the binary-tree structure

were used as training data of a CPN with a large mapping space. Results revealed that data

expansion is performed based on the similarity and continuity of training data, and that

more facial expression patterns such as mixed facial expressions between categories can be

generated in the CPN mapping space. It is expected that the use of an FEMap generated

using the proposed method can be useful as a classifier in facial expression recognition that

contributes to improvement in generalization capability.

This chapter specifically described a generation method of an FEMap and used facial

expression images obtained during the same period. However, it is difficult to obtain all of a

subject’s facial expression patterns at one time; in addition, faces age with time. In future

studies, we intend to take aging of a facial expression pattern into consideration, and study

an automatic FEMap updating method using additional learning functions.

7. Acknowledgments

This work was supported in part by Ministry of Education, Culture, Sports, Science and

Technology (MEXT) Grants-in-Aid for Young Scientists (B): No. 18700192 and No. 20700174.

This chapter is based on “Generation of Facial Expression Map based on Topological

Characteristics of Face Images,” by M. Ishii, K. Sato, H. Madokoro and M. Nishida, which

appeared in the Proceedings of the IEEE International Conference on Systems, Man and

8. References

Akamatsu, S. (1997). Computer Recognition of Human Face –A Survey-, IEICE trans.

Information and systems, Pt.2 (Japanese Edition), Vol.J80-D-II, No.8, pp.2031-2046.

Ekman, P. & Friesen, W.V. (1978). Facial Action Coding System, Consulting Psychologist Press.

Fasel, B., & Luettin, J. (2003). Automatic Facial Expression Analysis: A Survey, Pattern

Recognition, Vol.36, pp.259-275.

Gross, R. (2005). Face Databases, Handbook of Face Recognition, S.Li and A.Jain, ed., Springer-

Verlag.

Hasegawa, O.; Morishima, S. & Kaneko, M. (1997). Processing of Facial Information by

Computer, IEICE trans. Information and systems, Pt.2 (Japanese Edition), Vol.J80-D-II,

No.8, pp.2047-2065.

Kohonen, T. (1995). Self-Organizing Maps, Springer Series in Information Sciences.

Lyons, M.J.; Budynek, J. & Akamatsu, S. (1999). Automatic Classification of Single Facial

Images, IEEE Trans. Pattern Analysis and Machine Intelligence, Vol.21, No.12, pp.1357-

1362.

Lyons, M.J.; Akamatsu, S., Kamachi, M. & Gyoba, J. (1998). Coding Facial Expressions with

GaborWavelets, Proc. IEEE Int. Conf. Automatic Face and Gesture Recognition, pp.200-

205.

Nielsen, R.H. (1987). Counterpropagation Networks, Applied Optics, vol.26, No.23, pp.4979-

4984.

Pantic, M.; Valstar, M.F., Rademaker, R. & Maat, L. (2005). Webbased Database for Facial

Expression Analysis, Proc. IEEE Int. Conf. Multimedia and Expo, pp.317-321.

Machine Learning

258

Pantic, M. & Rothkrantz, L.J.M. (2000a). Automatic Analysis of Facial Expressions: The State

of the Art, IEEE Trans. Pattern Analysis and Machine Intelligence, Vol.22, No.12,

pp.1424-1445.

Pantic, M. & Rothkrantz, L.J.M. (2000b). Expert System for Automatic Analysis of Facial

Expression, Image and Vision Computing, Vol.18, No.11, pp.881-905.

Tian, Y.L.; Kanade, T. & Cohn, J.F. (2001). Recognizing Action Units for Facial Expression

Analysis, IEEE Trans. Pattern Analysis and Machine Intelligence, Vol.23, No.2, pp.97-

116.

Yang, M.; Kriegman, D.J. & Ahuja, N. (2002). Detecting Faces in Images: A Survey, IEEE

Trans. Pattern Analysis and Machine Intelligence, Vol.24, No.1, pp.34-58.

Zhang, Z.; Lyons, M., Schuster, M. & Akamatsu, S. (1998). Comparison Between Geometry-

Based and Gabor-Wavelet-Based Facial Expression Recognition Using Multi-Layer

Perceptron, Proc. IEEE Int. Conf. Automatic Face and Gesture Recognition, pp.454-459.

Zhao, W.; Chellappa, R., Rosenfeld, A. & Phillips, P.J. (2000). Face Recognition: A Literature

Survey, Technical Report 00-948, University of Maryland.

Linear Subspace Learning for

Facial Expression Analysis

Caifeng Shan

Philips Research

The Netherlands

1. Introduction

Facial expression, resulting from movements of the facial muscles, is one of the most

powerful, natural, and immediate means for human beings to communicate their emotions

and intentions. Some examples of facial expressions are shown in Fig. 1. Darwin (1872) was

the first to describe in detail the specific facial expressions associated with emotions in

animals and humans; he argued that all mammals show emotions reliably in their faces.

Psychological studies (Mehrabian, 1968; Ambady & Rosenthal, 1992) indicate that facial

expressions, with other non-verbal cues, play a major and fundamental role in face-to-face

communication.

Fig. 1. Facial expressions of George W. Bush.

Machine analysis of facial expressions, enabling computers to analyze and interpret facial

expressions as humans do, has many important applications including intelligent human-

computer interaction, computer animation, surveillance and security, medical diagnosis,

law enforcement, and awareness system (Shan, 2007). Driven by its potential applications

and theoretical interests of cognitive and psychological scientists, automatic facial

expression analysis has attracted much attention in last two decades (Pantic & Rothkrantz,

2000a; Fasel & Luettin, 2003; Tian et al, 2005; Pantic & Bartlett, 2007). It has been studied in

multiple disciplines such as psychology, cognitive science, computer vision, pattern

Machine Learning

260

recognition, and human-computer interaction. Although much progress has been made, it is

still difficult to design and develop an automated system capable of detecting and

interpreting human facial expressions with high accuracy, due to their subtlety, complexity

and variability.

Many machine learning techniques have been introduced for facial expression analysis, such

as Neural Networks (Tian et al, 2001), Bayesian Networks (Cohen et al, 2003b), and Support

Vector Machines (SVM) (Bartlett et al, 2005), to name just a few. Meanwhile, appearance-

based statistical subspace learning has been shown to be an effective approach to modeling

facial expression space for classification. This is because that despite a facial image space

being commonly of a very high dimension, the underlying facial expression space is usually

a sub-manifold of much lower dimensionality embedded in the ambient space. Subspace

learning is a natural approach to resolve this problem. Traditionally, linear subspace

methods including Principal Component Analysis (PCA) (Turk & Pentland, 1991), Linear

Discriminant Analysis (LDA) (Belhumeur et al, 1997), and Independent Component

Analysis (ICA) (Bartlett et al, 2002) have been used to discover both facial identity and

expression manifold structures. For example, Lyons et al (1999) adopted PCA based LDA

with the Gabor wavelet representation to classify facial images, and Donato et al (1999)

explored PCA, LDA, and ICA for facial action classification.

Recently a number of nonlinear techniques have been proposed to learn the structure of a

manifold, e.g., Isomap (Tenenbaum et al, 2000), Local Linear Embedding (LLE) (Roweis &

Saul, 2000; Saul & Roweis, 2003), and Laplacian Eigenmaps (Belkin & Niyogi, 2001, 2003).

These methods have been shown to be effective in discovering the underlying manifold.

However, they are unsupervised in nature and fail to discover the discriminant structure in

the data. Moreover, these techniques yield maps that are defined only on the training data,

and it is unclear how to evaluate the maps for new test data. So they may not be suitable for

pattern recognition tasks such as facial expression recognition. To address this problem,

some linear approximations to these nonlinear manifold learning methods have been

proposed to provide an explicit mapping from the input space to the reduced space (He &

Niyogi, 2003; Kokiopoulou & Saad, 2005). He and Niyogi (2003) developed a linear subspace

technique, known as Locality Preserving Projections (LPP), which builds a graph model that

reflects the intrinsic geometric structure of the given data space, and finds a projection that

respects this graph structure. LPP can be regarded as a linear approximation to Laplacian

Eigenmaps; it can easily map any new data to the reduced space by using a transformation

matrix. By incorporating the priori class information into LPP, we presented a Supervised

LPP (SLPP) approach to enhance discriminant analysis on a manifold structure (Shan et al,

2005a). Cai et al (2006) further introduced a Orthogonal LPP (OLPP) approach to produce

orthogonal basis vectors, which potentially have more discriminating power.

Orthogonal Neighborhood Preserving Projections (ONPP) is another interesting linear

subspace technique proposed recently (Kokiopoulou & Saad, 2005, 2007). ONPP aims to

preserve the intrinsic geometry of the local neighborhoods; it can be regarded as a linear

approximation to LLE. ONPP constructs a weighted k-nearest neighbor graph which models

explicitly the data topology, and, similarly to LLE, the weights are decided in a data-driven

fashion to capture the geometry of local neighborhoods. In contrast to LLE, ONPP computes

an explicit linear mapping from the input space to the reduced space. ONPP can be

performed in either an unsupervised or a supervised setting. More recently Cai et al (2007)

introduced a linear subspace method called Locality Sensitive Discriminant Analysis

Linear Subspace Learning for Facial Expression Analysis

261

(LSDA), which finds a projection that maximizes the margin between data points from

different classes at each local area. LSDA constructs a nearest neighbor graph to model the

geometrical structure of the underlying manifold, and then split it into within-class graph

and between-class graph by using the class labels. LPP, ONPP, LSDA are all linear subspace

learning techniques which aim at preserving locality of data samples, relying on a nearest

neighbor graph to capture the data topology. However, they adopt totally different objective

functions, so potentially they will provide different subspace learning power.

As different linear subspace techniques have been developed, the researchers are therefore

confronted with a choice of algorithms with significantly different strengthes. However, to

our best knowledge, there is no comprehensive comparative study on these linear subspace

methods using the same data and experimental settings, although they were individually

evaluated. In particular, for the task of facial expression analysis, it is necessary and

important to identify the most effective linear subspace technique for facial expression

representation and classification. In this chapter, we investigate and evaluate a number of

linear subspace techniques for modeling facial expression subspace. Specifically we compare

LPP and its variants SLPP and OLPP, ONPP, LSDA with the traditional PCA and LDA

using different facial representations on several public databases. We find in our extensive

study that the supervised LPP provides the best results in learning facial expression

subspace, resulting in superior facial expression recognition performance. A short version of

our work was presented in (Shan et al, 2006a).

The remainder of this chapter is organized as follows. We first survey the state of the art of

facial expression analysis with machine learning (Section 2). Different linear subspace

techniques compared in this chapter are described in Section 3. We present extensive

experiments on different databases in Section 4, and finally Section 5 concludes the chapter.

2. State of the art

After Suwa et al (1978) made an early attempt to automatically analyze facial expressions

from image sequences, machine analysis of facial expressions has received much attention in

last two decades (Pantic & Rothkrantz, 2000a; Fasel & Luettin, 2003; Tian et al, 2005; Pantic

& Bartlett, 2007). In this section, we review the state of the art on applying machine learning

techniques for facial expression analysis.

Facial expressions can be described at different levels. Two mainstream description methods

are facial affect (emotion) and facial muscle action (action unit) (Pantic & Bartlett, 2007).

Most of facial expression analysis systems developed so far target facial affect analysis,

attempting to analyze a set of prototypic emotional facial expressions (Pantic & Rothkrantz,

2000a, 2003). To describe subtle facial changes, Facial Action Coding System (FACS) (Ekman

et al, 2002) has been used for manually labeling of facial actions. FACS associates facial

changes with actions of the muscles that produce them. It defines 44 different action units

(AUs). Another possible descriptor is the bipolar dimensions of Valence and Arousal (Russell,

1994). Valence describes the pleasantness, with positive (pleasant) on one end (e.g.

happiness), and negative (unpleasant) on the other (e.g. disgust). The other dimension is

arousal or activation, for example, sadness has low arousal, whereas surprise has a high

arousal level.

The general approach to automatic facial expression analysis consists of three steps: face

acquisition, facial data extraction & representation, and facial expression recognition. In the

following sections, we discuss these steps respectively.

Machine Learning

262

2.1 Face acquisition

Face acquisition is a pre-processing stage to automatically detect or locate the face region in

the input images or sequences. Numerous techniques have been proposed for face detection

(Yang et al, 2002), due to its practical importance in many computer vision applications.

Most of existing methods emphasize statistical learning techniques and use appearance

features. The real-time face detection scheme proposed by Viola and Jones (2001) is arguably

the most commonly employed face detector, which consists of a cascade of classifiers trained

by AdaBoost employing Harr-wavelet features. AdaBoost (Freund & Schapire, 1997;

Schapire & Singer, 1999) is one of the most successful machine learning techniques applied

in computer vision area, which provides a simple yet effective approach for stagewise

learning of a nonlinear classification function. AdaBoost learns a small number of weak

classifiers whose performance are just better than random guessing, and boosts them

iteratively into a strong classifier of higher accuracy. Lienhart et al (2003) later made some

extensions to this face detector. Many other machine learning techniques such as Neural

Networks and SVM have also been introduced for face detection; details can be found in

(Yang et al, 2002).

Most of face detectors can only detect faces in frontal or near-frontal view. To handle large

head motion in video sequences, head tracking and head pose estimation can be adopted.

The tasks of head tracking and pose estimation can be performed sequentially or jointly.

Different approaches have been developed for head pose estimation (Murphy-Chutorian &

Trivedi, 2008). Given the success of frontal face detectors, a natural extension is to estimate

head pose by training multiple face detectors, each to specific a different discrete pose. For

example, cascade AdaBoost detectors have been extended for pose estimation (Jones &

Viola, 2003). Recently manifold learning approaches have been adopted to seek low-

dimensional manifolds that model the continuous variation in head pose; new images can

then be embedded into these manifolds for pose estimation. Nonlinear methods such as

Isomap, LLE, and Laplacian Eigenmaps or their linear approximations have been exploited

for pose estimation (Fu & Huang, 2006; Balasubramanian et al, 2008).

2.2 Facial feature extraction & representation

Facial feature extraction and representation is to derive a set of features from original face

images which are used for representing faces. Two types of features, geometric features and

appearance features, are usually considered for facial representation. Geometric features

deal with the shape and locations of facial components (including mouth, eyes, brows, and

nose), which are extracted to represent the face geometry (Zhang et al, 1998; Pantic &

Rothkrantz, 2000b; Tian et al, 2001; Kaliouby & Robinson, 2004; Zhang & Ji, 2005; Pantic &

Bartlett, 2007). Appearance features present the appearance changes (skin texture) of the

face (including wrinkles, bulges and furrows), which are extracted by applying image filters

to either the whole face or specific facial regions (Lyons et al, 1999; Donato et al, 1999;

Bartlett et al, 2003; Shan et al, 2005c; Littlewort et al, 2006; Gritti et al, 2008). The geometric

features based facial representations commonly require accurate and reliable facial feature

detection and tracking, which is difficult to accommodate in real-world unconstrained

scenarios, e.g., under head pose variation. In contrast, appearance features suffer less from

issues of initialization and tracking errors, and can encode changes in skin texture that are

critical for facial expression modeling. However, most of the existing appearance-based

facial representations still require face registration based on facial feature detection, e.g., eye

detection.