Меледин Т.В., Черкасский В.С. Электродинамика в задачах. Часть 1. Электродинамика частиц и полей

Подождите немного. Документ загружается.

1 ЭЛЕКТРОСТАТИКА В ВАКУУМЕ

в) Поле, создаваемое плоскостью с отверстием, можно рассматри-

вать как суперпозицию двух полей: поля плоскости без отверстия, за-

ряженной с плотностью σ, и поля диска радиуса R, заполняющего

отверстие и заряженного с плотностью −σ. Поэтому

= 2πσ

|z|

− 2πσ



|z|

−

√

+ z



= 2πσ

√

+ z

Распределение потенциала на оси отверстия

ϕ =

dz + const = −2πσ

√

+ z

+ const .

Константу можно выбрать равной нулю, это будет означать, что по-

тенциал в центре отверстия ϕ(0) = −2πσR.

Р.9. Используя теорему Гаусса, найти поля равномерно заряжен-

ных:

а) шарика радиуса a с объемной плотностью ρ;

б) бесконечного цилиндра радиуса a с линейной плотностью η;

в) бесконечного плоского слоя толщины 2a с объемной плотностью

заряда ρ.

Эти задачи, обладают такой симметрией распределения зарядов,

что можно, не решая, указать поверхности, на которых напряженность

электрического поля

E перпендикулярна ей в каждой точке и посто-

янна по величине. Для нахождения поля

E в таких задачах достаточ-

но применения теоремы Гаусса, смысл которой для вакуума состоит

в следующем: поток вектора напряженности электрического поля че-

рез замкнутую поверхность S равен полному заряду, заключенному

внутри нее (умноженному на 4π в системе CGSE). Математическое

выражение теоремы Гаусса имеет вид

(

E d~s) = 4π

ρ dv, (1)

1.5 Решение типичных задач

где d~s — вектор, по величине равный величине элементарной пло-

щадки ds, а по направлению совпадает с направлением внешней нор-

мали к этой площадке, т. е. нормали, направленной наружу; ρ — объ-

емная плотность заряда. Интеграл с левой стороны есть поток вектора

E через замкнутую поверхность S. Под интегралом соответсвенно

стоит скалярное произведение векторов

E и d~s, равное потоку век-

тора

E через малую площадку ds. Интеграл с правой стороны бе-

рется по объему, заключенному внутри поверхности, и равен полному

заряду, находящемуся в нем. Успех решения с помощью соотношения

(1) обусловливается тем, что, выбирая поверхность интегрирования,

на которой напряженность поля E постоянна, можно E вынести за

знак интеграла и тогда это соотношение дает возможность найти

а) Совместим начало сферической системы координат с центром

шара. Ввиду сферической симметрии распределе-

ния заряда ясно, что вектор

E может быть направ-

лен только вдоль радиуса и зависеть только от ве-

личины радиуса. Поток вектора

E через сфериче-

скую поверхность радиуса R независимо от вели-

чины радиуса запишется так:

Φ =

(

E d~s) = E

ds = E · 4πR

если

E параллелен радиус-вектору

R и Φ = −E ·4πR

, если

E ан-

типараллелен

R, поскольку косинус угла между

E и d~s будет равен

(-1).

С другой стороны,

4π

ρdv = 4πρ ·

πR

при R ≤ a

4π

ρdv = 4πρ ·

πa

при R > a .

1 ЭЛЕКТРОСТАТИКА В ВАКУУМЕ

Поэтому

E =

πρ

R при R ≤ a,

E =

πρa

R при R > a ,

где Q =

πa

ρ — полный заряд шара.

Таким образом, равномерно заряженный шар создает во внешнем

пространстве такое поле, как если бы весь заряд был сосредоточен в

его центре. Этот результат остается справедливым при любом сфери-

чески симметричном распределении заряда по объему шара.

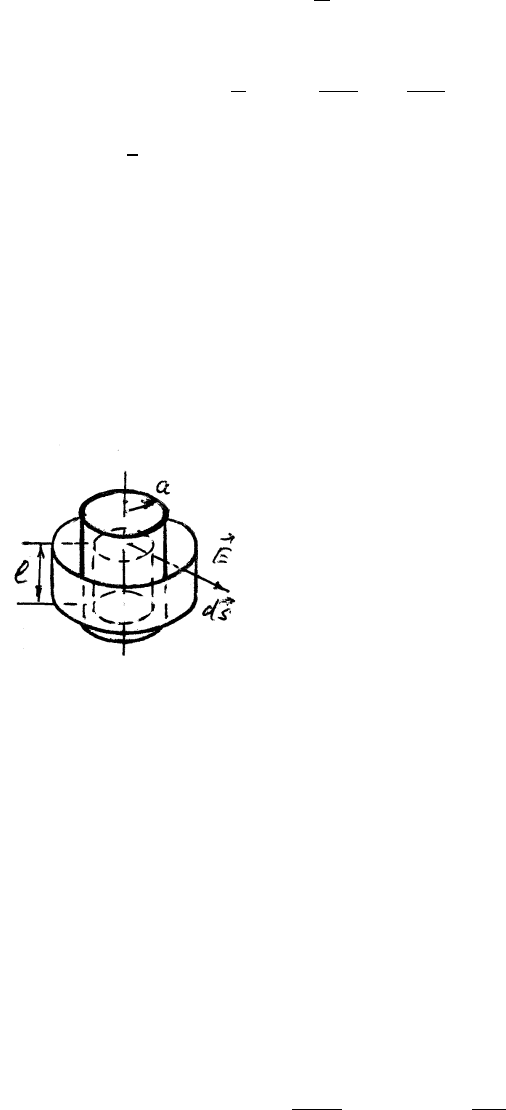
б) Для бесконечного равномерно заряженного цилиндра вектор на-

пряженности электрического поля лежит в плоскостях, перденди-

кулярных оси цилиндра, и может зависеть только

от расстояния от точки наблюдения до оси цилин-

дра. В цилиндрической системе координат с осью

Z вдоль оси цилиндра вектор напряженности

направлен вдоль ~r. Построим два коаксиальных

цилиндра длины l с радиусами r < a и r > a.

Поток вектора

E через поверхность каждого из цилиндров запишет-

ся так

Φ =

(

E d~s) = E

ds = E · 2πrl.

При вычислении потока мы считали, что ρ > 0, и, значит, вектор

d~s направлен по ~r. Поток вектора

E через торцы цилиндров равен

нулю, поскольку на них

E и ~r перпендикулярны.

С другой стороны,

4π

ρ dv = 4π

πa

dv =

4η

πr

l при r < a,

4π

ρ dv = 4πρ · πa

l = 4πη l при r ≥ a.

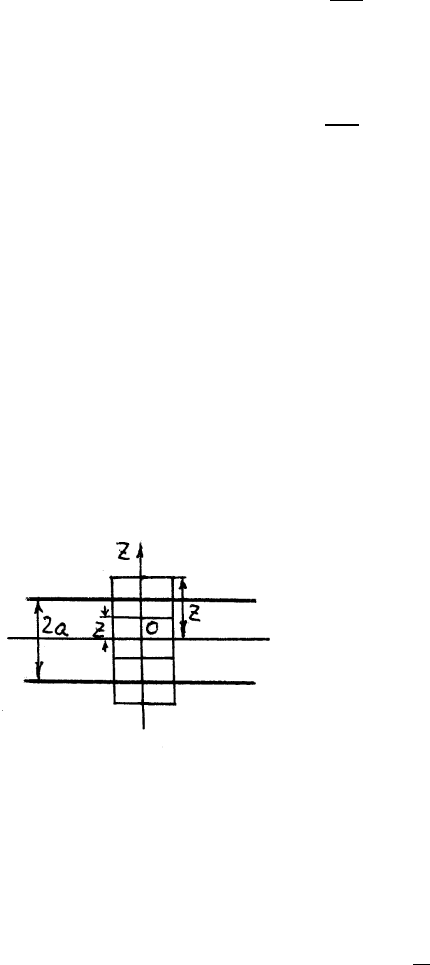
1.5 Решение типичных задач

Подставляя найденные значения в уравнение (1), получаем

E =

2η

~r при r ≤ a,

E =

2η

~r при r > a.

в) Пусть средняя плоскость пластинки занимает положение плос-

кости (x , y). В силу симметрии распределения заряда относительно

плоскости (x , y), вектор

E может зависеть только от координаты z

и направлен от плоскости, если пластина заряжена положительно, и к

плоскости, если ее заряд отрицателен.

Построим куб с основаниями, симметрично расположенными по раз-

ные стороны от средней плоскости. Если S — площадь каждого

основания, то поток вектора

E через оба основания равен 2ES.

Поток через боковую поверхность куба ра-

вен нулю, так как на ней векторы

E и d~s

взаимно перпендикулярны. Значит, поток че-

рез поверхность куба равен 2ES. С другой

стороны, правая сторона выражения (1) будет

равна: 4πηS · |z|, если z ≤ a, и 4πηS · 2a, если z > a. Поэтому

E = 4πη~z при |z| ≤ a ,

E = 4πηa

при |z| > a .

Р.10. Внутри шара радиуса a, равномерно заряженного по объему

с плотностью ρ, имеется незаряженная шарообразная полость, радиус

которой b , а центр отстоит от центра шара на расстоянии l таком, что

(l + b < a). Найти электрическое поле

E в полости.

Поле, создаваемое шаром с полостью, можно рассматривать как

1 ЭЛЕКТРОСТАТИКА В ВАКУУМЕ

суперпозицию двух полей: поля сплошного ша-

ра радиуса a, заряженного с плотностью ρ, и

поля сплошного шара радиуса b, заполняюще-

го полость с объемной плотностью −ρ. Нуле-

вой заряд полости представлен как ρ+(−ρ) =

0. Тогда, используя результат задачи Р.9а, на-

ходим поле в полости

E =

πρ

R −

πρ~r =

πρ

l .

Поле внутри полости однородное и направлено по линии, соединя-

ющей центр шара с центром полости, в сторону центра полости.

Р.11. Найти силу и вращательный момент, приложенные к электри-

ческому диполю с моментом

P в поле точечного заряда q.

Сила, действующая на диполь в поле точечного заряда q, является

суммой сил, действующих на заряды диполя со стороны заряда q:

F =

= Q(

−

) , (1)

где

— напряженность электрического поля, создаваемая зарядом

q в точке нахождения отрицательного заряда диполя ( −Q);

— в

точке нахождения положительноного заряда диполя. Если

расстояние между зарядами диполя мало по

сравнению с расстоянием, на котором находит-

ся диполь от заряда, то поле

можно разло-

жить в ряд Тейлора и оставить в нем два пер-

вых отличных от нуля члена

R +

l ) =

R) + l

∂

∂x

+ l

∂

∂y

+ l

∂

∂z

≈

+ (

∇)

E ,

где (

∇) — скалярное произведение вектора

E и вектора

∇ =



∂

∂x

∂

∂y

∂

∂z



. Подставим

в уравнение (1) и учитывая,

1.5 Решение типичных задач

что

P = Q

E =

R, находим выражение для силы, действующей

на диполь со стороны точечного заряда:

F = (

∇)

R = q



∂

∂x

+ P

∂

∂y

+ P

∂

∂z



. (2)

Так как

∂

∂x





= P



∂

∂x

∂

∂x







= P



−



то аналогично

∂

∂y





= P



−



, P

∂

∂z





= P



−



где

k — единичные векторы в направлениях соответственно

X, Y , Z. Подставляя вычисленные соотношения в уравнение (2), по-

лучаем

F = q



−



. (3)

Сила, действующая на диполь в поле точечного заряда, равна по аб-

солютной величине и противоположна по направлению силе, действу-

ющей на заряд в поле диполя. Поэтому из формулы (3) следует, что

поле, создаваемое диполем в точке, определяемой радиус-вектором

на больших расстояниях, будет иметь вид

дип

−

Момент сил, действующий на диполь во внешнем поле

E, равен

N = [

P ×

E]. Подставляя в эту формулу поле точечного заряда

E = q

R/R

, получаем

N = q

[

P ×

1 ЭЛЕКТРОСТАТИКА В ВАКУУМЕ

где

R — радиус-вектор, проведенный из точки нахождения точечного

заряда q в точку, где находится диполь.

Р.12. а) Показать, что дипольный момент

P электрически ней-

тральной системы зарядов

= 0 не меняется при смещении на-

чала координат.

б) При каком выборе вектора смещения

d дипольный момент

= 0, если

6= 0?

а) Пусть в некоторой системе координат радиус-вектор положе-

ния заряда q

есть

, тогда дипольный момент системы зарядов в

этой системе координат

P =

. Сдвинем начало координат на

некоторый вектор

d, тогда положение каждого заряда в новой системе

будет

−

d и

(

−

d) =

−

P ,

так как

= 0.

б)

= 0, если

d =

Р.13. Найти потенциал ϕ (

R) поля двух концентрических колец ра-

диусов a и b с зарядами q и −q для: а) R  a, b; б) R  a, b.

Сначала вычислим потенциал от одного

кольца на больших расстояниях. Заряженное

кольцо радиуса R

расположим в плоскости

(x, y). Центр кольца 0 совпадает с началом

координат. Ось X направим перпендикуляр-

но плоскости, в которой лежат Z и

1.5 Решение типичных задач

R — радиус-вектор точки наблюдения. Потенциал, создаваемый за-

рядом элемента кольца dl = R

dα, в точке (R, θ) равен

dϕ =

2πR

dα

+ R

− 2RR

cos θ

Потенциал, создаваемый зарядом всего кольца:

ϕ =

2π

dα

+ R

− 2RR

cos θ

. (1)

Чтобы найти потенциал на расстояниях, больших по сравнению с ра-

диусом кольца, разложим подынтегральное выражение в ряд Тейлора

по малому параметру R

/R до второго порядка включительно. По-

скольку дипольный момент кольца равен нулю, что видно из симмет-

рии расположения зарядов, то оставим в сумме три первых члена:

+ R

− 2RR

cos θ

1 + (

)

−

cos θ

1 +

cos θ





(3 cos

− 1) + . . .

Вычисляя теперь интеграл (1), получаем

ϕ =





(1 − 3 cos

) .

При вычислении использована связь cos θ

= sin θ sin α. Значит,

потенциал от двух концентрических колец радиусов a и b с зарядами

q и −q имеет вид

ϕ (R, θ) =

− b

)(1 − 3 cos

) при a, b  R.

1 ЭЛЕКТРОСТАТИКА В ВАКУУМЕ

Теперь найдем потенциал кольца радиуса R

при R

 R :

ϕ (R, θ) =

2πR





2π

(3 sin

θ sin

α − 1) dα =





(1 − 3 cos

Тогда потенциал двух колец при a, b  R будет иметь вид

ϕ(R, θ) = q



−



−



−



(3 cos

θ − 1) .

Р.14. Три бесконечные заряженные нити (линейная плотность заря-

да η) расположены на расстоянии a друг от друга. Найти два первых

(отличных от нуля) члена разложения потенциала на больших рассто-

яниях.

Напряженность электрического поля от бесконечной заряженной

с плотностью η нити

E = (2η/R

)

R, где

— радиус-вектор, расположенный в плоско-

сти, перпендикулярной нити, и проведенный от

нити в точку наблюдения. Тогда потенциал от

одной нити равен −2η ln R+ const. Потенци-

ал от трех нитей в обозначениях рисунка

ϕ = −2η ln r

− 2η ln r

Константа выбрана равной нулю. Так как ~r

= ~r −

, то

= (r

+ b

− 2rb sin α)

1/2

Аналогично



+ b

− 2rb cos(α + 30

◦

)



1/2

= (r

+ b

+ 2rb cos(α − 30

◦

))

1/2

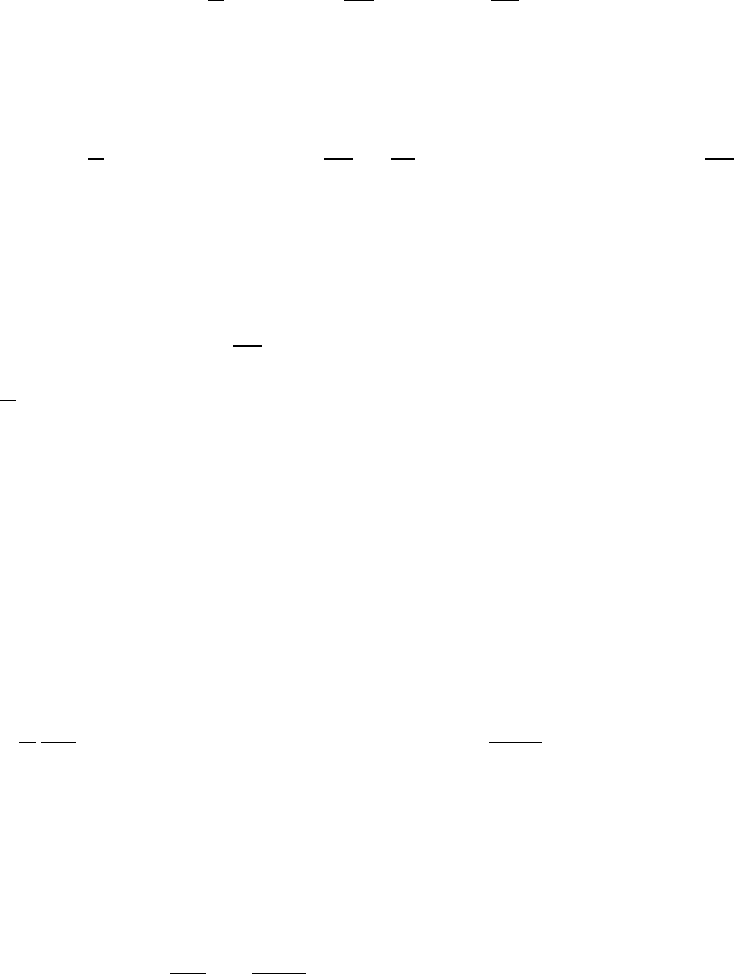
1.5 Решение типичных задач

где b = |

| = |

|. Далее,

ln r

= ln r +



1 −

sin α +



Разлагая второе слагаемое в ряд Тейлора по степеням b/r, получаем

ln r

' ln r −sin α

+ (1 −2 sin

α)

(12 sin α −16 sin

α)

Сделав аналогичные вычисления для ln r

и ln r

и сложив, оконча-

тельно найдем, что

ϕ = −6η ln r − 2

η sin

α при b << r,

где b = a/

√

Р.15. По какому закону должна быть распределена плотность заря-

да ρ (r) внутри цилиндра радиуса R, чтобы напряженность электри-

ческого поля E внутри цилиндра была постоянна по величине и равна

. Каково распределение потенциала?

Из div

E = 4πρ следует

∂

∂r

(rE

) = 4πρ, откуда ρ =

4πr

Внутри цилиндра потенциал ϕ изменяется по закону ϕ

= −E

r+C,

где C — константа. Вне цилиндра потенциал подчиняется уравнению

Лапласа, которое для данного случая будет иметь вид

∂

∂r



∂ϕ

∂r



= 0.

Откуда

= A ln r + B,

где A, B — константы. Выбирая ϕ

(0) = 0 и используя граничные

условия

(R) = ϕ

(R),