Меледин Т.В., Черкасский В.С. Электродинамика в задачах. Часть 1. Электродинамика частиц и полей

Подождите немного. Документ загружается.

120

4 МАГНИТНОЕ ПОЛЕ В ВАКУУМЕ

1a) Пусть

B направлено по оси Z. Положим A

= 0, посколь-

ку циркуляция вектора

A максимальна в плоскости (X,Y ). Вектор-

ное уравнение (1) равносильно трем скалярным уравнениям, которые

с учетом A

= 0 запишутся в виде

∂A

∂x

−

∂A

∂y

= B

∂A

∂z

= 0 , (5)

∂A

∂z

= 0 .

Решение этой системы не однозначно. Из двух последних уравнений

следует, что A

и A

могут быть только функциями от x и y и удо-

влетворяют уравнению

∂A

∂x

∂A

∂y

= 0 . (6)

Решение уравнения (6) можно выбрать, например,

= 0, A

= A

(y).

Подставляя их в уравнение (5), находим

= B

· y.

Более симметричное решение уравнения (6) имеет вид

= b · x + A

(y) ,

= −b · y + A

(x) ,

где b — произвольная постоянная. Подставляя это решение в урав-

нение (5), получаем

∂A

(x)

∂x

−

∂A

(y)

∂y

= B

= const .

4.3 Решение типичных задач

121

Откуда

(y) = −

· y , A

(x) =

· x .

Выбирая b = 0, окончательно находим

= −

· y , A

· x , A

= 0 .

1б) В цилиндрической системе координат ( z, r, α) уравнение (1)

будет равносильно уравнениям

∂

∂r

(rA

) −

∂A

∂α

= B

∂A

∂α

−

∂A

∂z

= 0 ,

∂A

∂z

−

∂A

∂r

= 0 .

Полагая A

= 0, как и в декартовой системе координат, уравнения

принимают вид

∂

∂r

(rA

) −

∂A

∂α

= B

∂A

∂z

= 0 , (7)

∂A

∂z

= 0 .

Выбирая A

= 0, из уравнения (7) находим

1в) В сферической системе координат ( R,θ,α) проекциями вектора

B будут:

= B cos θ , B

= −B sin θ , B

= 0 .

Выбираем вектор

A (как и в предыдущих случаях) лежащим в плос-

костях, перпендикулярных

B. Тогда у

A существует только отличная

122

4 МАГНИТНОЕ ПОЛЕ В ВАКУУМЕ

от нуля проекция A

. Полагая A

= A

= 0, скалярные уравнения,

соответствующие векторному уравнению (1), будут иметь вид

R sin θ

∂

∂θ

(sin θ A

) = B cos θ , (8)

∂A

∂R

= B sin θ . (9)

Интегрируя уравнение (8), получаем

BR sin θ + f(R) ,

где f(R) — произвольная функция от R. Из симметрии задачи сле-

дует, что A

не зависит от α. Подставляя A

в уравнение (9),

получаем ∂f(R)/∂R = 0, значит, f(R) можно выбрать равным ну-

лю, f(R) = 0. Окончательно

= A

= 0 , A

BR sin θ .

2) Будем решать задачу в цилиндрической системе координат.

Пусть ток J течет вдоль оси Z . Тогда из уравнения (3) следует, что

векторный потенциал можно выбрать направленным тоже по Z. На-

пряженность магнитного поля прямого тока имеет только α-ю компо-

ненту: H

= 2J/cr. Запишем проекцию векторного уравнения (1)

на α-е направление:

= −

∂A

∂r

. (10)

3десь положено µ = 1. Интегрируя уравнение (10), получаем

= −

ln r + const .

Константа произвольна. Можно приписать точкам произвольной ци-

линдрической поверхности, соосной с током, нулевой векторный по-

тенциал.

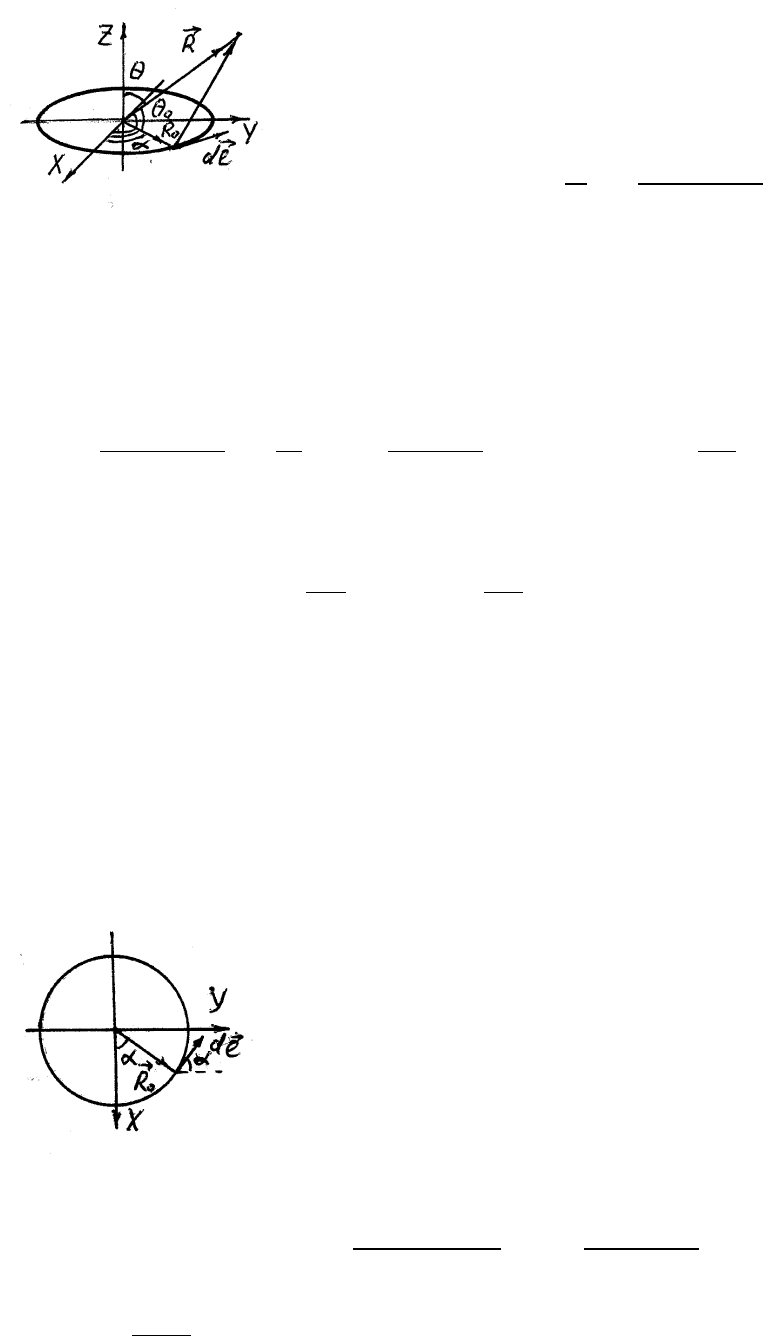
3) Кольцо с током радиуса R

расположено в плоскости (X, Y ).

4.3 Решение типичных задач

123

Найдем векторный потенциал в точке наблю-

дения, задаваемой радиус-вектором

R. Для

линейного тока выражение (4) запишется так:

R) =

R −

. (11)

Направим ось X перендикулярно плоскости, в которой лежат Z и

(см. рисунок). На больших расстояниях подынтегральное выражение

(11) можно представить так:

R −

≈



1 +

(

)



при

 1 .

Тогда

R) =



l +

(

) d



. (12)

Первый интеграл равен нулю. Подынтегральное выражение второ-

го интеграла представим в виде

(

l = RR

cos θ

(−~n

sin α + ~n

cos α) dα =

= RR

sin θ sin α (−~n

sin α + ~n

cos α) dα , (13)

где ~n

, ~n

— единичные векторы в направлении осей X, Y . При

преобразовании использованы равенства

l = (−~n

sin α + ~n

cos α)R

dα ,

cosθ

= sin θ sin α .

Подставляя выражение (13) в уравнение (12)

и интегрируя по кольцу, окончательно получаем

R) = −

πR

J sin θ

[~m ×

где ~m =

πR

— магнитный момент кольца радиуса R

с током J.

124

4 МАГНИТНОЕ ПОЛЕ В ВАКУУМЕ

Р.45. Найти магнитный момент однородно заряженного шара (сфе-

ры), вращающегося вокруг одного из своих диаметров с угловой ско-

ростью ~ω. Заряд шара – Q, радиус – a.

а) Найдем магнитный момент сферы. Возьмем на поверхности сфе-

ры узкий поясок, заключенный между углами θ и θ + dθ. Заряд,

вращаясь вместе со сферой, создает ток, вели-

чина которого на выделенном пояске

dJ = υσa dθ =

4π

Qω sin θ dθ ,

где υ = ωa sin θ — скорость вращения пояс-

ка, σ = Q/4πa

— поверхностная плотность

заряда. Магнитный момент этого тока

d~m =

dJ ~s

πa

Q~ω

4πc

sin

θ dθ .

Интегрируя по θ, находим магнитный момент всей сферы:

~m =

d~m =

~ω

sin

θ dθ =

~ω

б) Найдем магнитный момент равномерно заряженного вращаю-

щегося вокруг одного из своих диаметров шара. Используя результат

предыдущей задачи, магнитный момент тонкого шарового слоя ради-

уса R толщины dR выразится так:

d~m =

~ωR

dQ ,

где dQ — заряд шарового слоя. Так как

dQ =

4πa

· 4πR

dR =

3QR

то магнитный момент шара будет равен

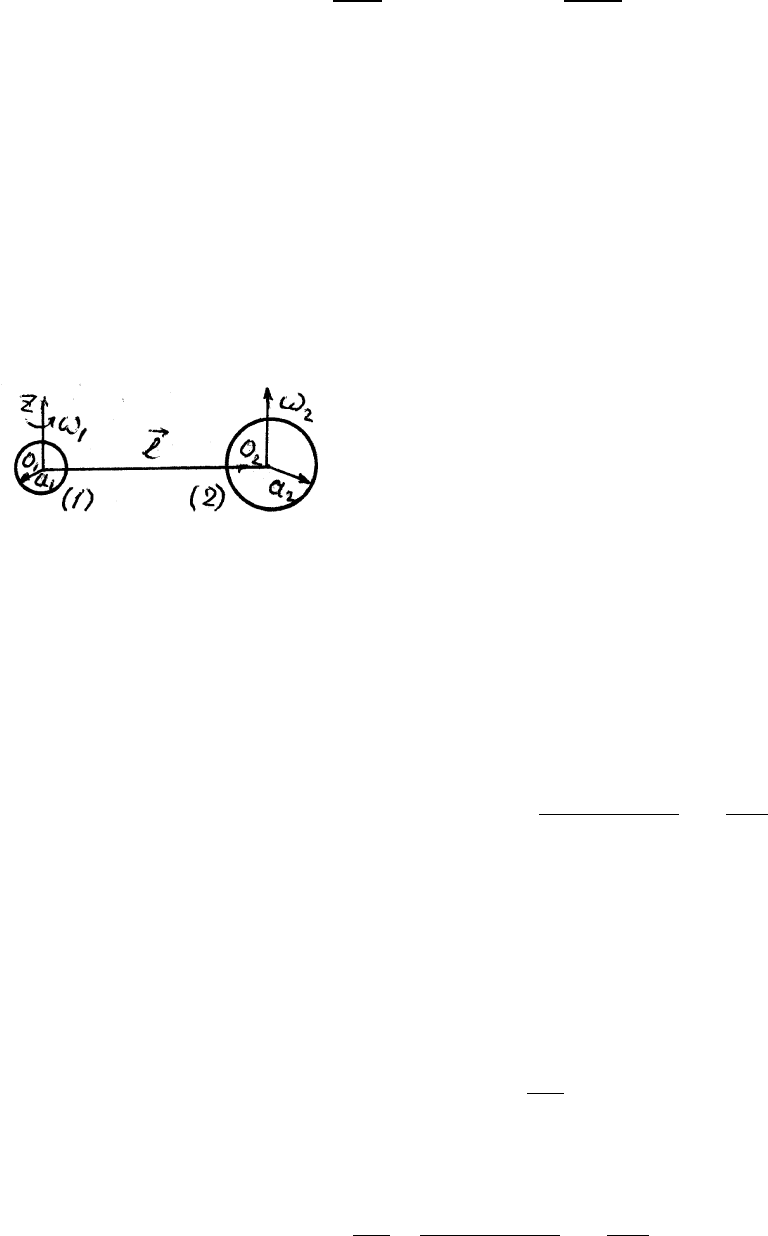
4.3 Решение типичных задач

125

~m =

Q~ω

dR =

~ω .

Р.46. Два равномерно заряженных шарика с зарядами q

, q

радиусами a

, a

вращаются без поступательного движения с угло-

выми скоростями ~ω

и ~ω

так, что векторы ~ω

, ~ω

перпендикулярны

отрезку

l, соединяющему центры шаров ( l  a

, a

). Оценить силу

взаимодействия шариков.

Выберем начало координат в центре шара (1). Ось Z совпадает с

направлением ~ω

, центр второго шара

находится на расстоянии l в плоскости

( X , Y ). Сила взаимодействия ша-

ров складывается из сил кулоновско-

го и магнитного взаимодействий. Она

может быть представлена как сила, действующая на шар 2 со стороны

шара 1. Поскольку расстояние между шарами велико по сравнению с

их размерами, то силу магнитного взаимодействия можно рассматри-

вать как силу взаимодействия двух магнитных моментов:

= (~m

∇)

R ~m

)

−

где ~m

1,2

= q

1,2

~ω

1,2

/5c;

— поле, создаваемое магнитным мо-

ментом ~m

на большом расстоянии, ~m

— магнитный момент шара

(2). Поскольку у ~m

есть только составляющая по Z, то скалярное

произведение вектора ~m

и вектора

∇ запишется так:

(~m

∇) = m

∂

∂z

а сила магнитного взаимодействия

= m

∂

∂z



R ~m

)

−



126

5 МАГНИТОСТАТИКА В СРЕДЕ

Далее, вычисляя производные по z, находим

∂

∂z



R ~m

)



3~m

−

15z

∂

∂z





= −

3~m

Подставляя в найденные выражения z = 0 ,

R =

l, окончательно

получаем

Таким образом, при l  a

, a

полная сила взаимодействия

F =

Силу магнитного взаимодействия можно представить и так:

= grad(~m

)



= grad

R ~m

)(

R ~m

)

−

(~m

)



= −grad

(~m

)



5. МАГНИТОСТАТИКА В СРЕДЕ

Закон Био–Савара в среде:

B =

l ×~r

j ×~r

µ [~v ×~r]

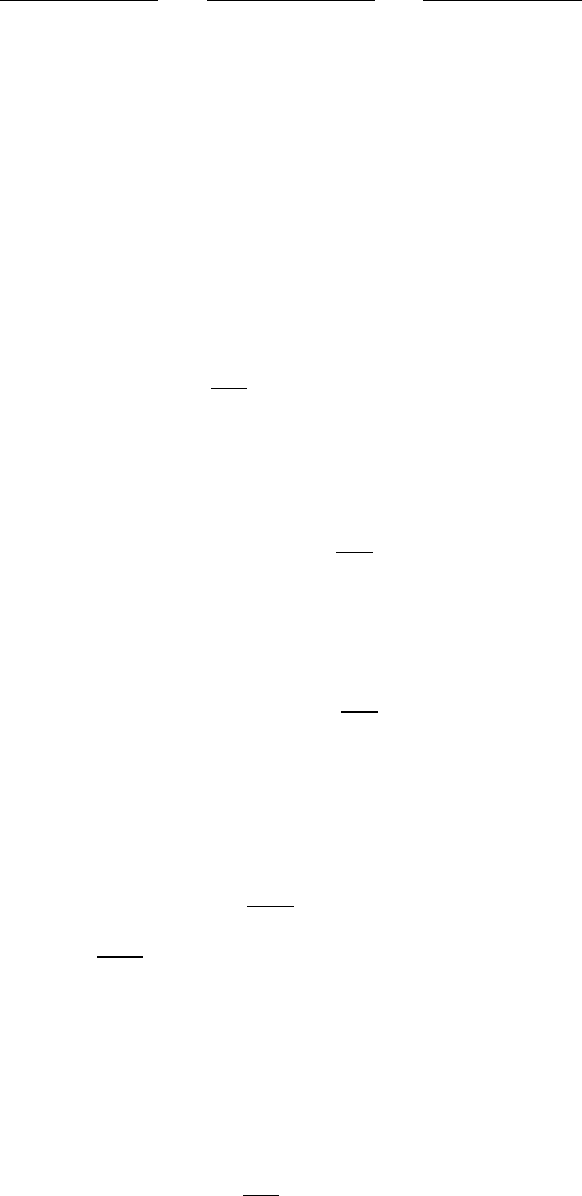
127

Сила Ампера в среде:

F =

l ×

j ×

~v ×

Вектор намагниченности

M – дипольный момент единицы объема

d~m =

MdV,

мол

= c rot

B =

H + 4π

Дифференциальные уравнения Максвела в среде:

div

B = 0, rot

H =

4π

j, где

H =

B − 4π

В интегральной форме:

B

dS = 0,

dl =

4π

dS.

Граничные условия:

| = B

1τ

| −

2τ

| =

4π

пов

×~n

Магнитная проницаемость µ = 1 – вакуум, µ & 1 – парамагнетик,

µ . 1 – диамагнетик, µ = 0 – сверхпроводник (эффект Мейснера),

µ  1 – ферромагнетик.

Энергия магнитного поля E =

µH

8π

dV , сила давления магнитного

поля F

pdS =

µH

8π

dS.

Правила Кирхгофа для потока магнитного поля:

= 0,

где

4π

JN.

128

5 МАГНИТОСТАТИКА В СРЕДЕ

5.1. Граничные условия для магнитного поля. Метод изображений. Постоян-

ные магниты. Магнитные цепи

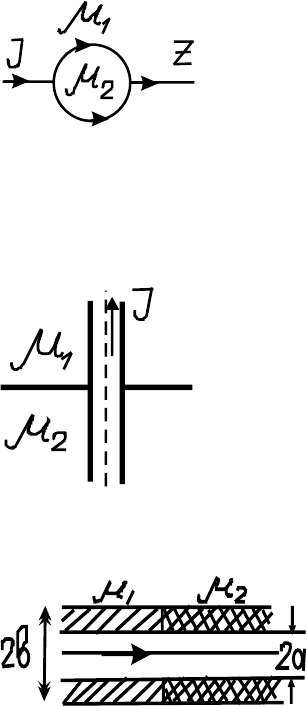
5.1. В пространстве, заполненном магнетиком с проницаемостью

, – бесконечный прямолинейный проводник с то-

ком J (вдоль оси Z). Проводящая сфера с центром

в начале координат (радиус её a ) заменяет соответ-

ствующую часть линейного проводника. Внутри сферы – магнетик с

проницаемостью µ

. Найти

B и

H всюду.

5.2. Цилиндрический проводник радиуса a проходит

перпендикулярно через плоскую границу раз-

дела двух магнетиков с проницаемостями µ

и µ

. По проводнику идет постоянный ток J.

Найти распределение полей

H и

B во всем

пространстве.

5.3. Прямой провод с постоянный током J проходит по оси сим-

метрии толстой трубы с радиусами a, b

(a < b). Одна половина трубы имеет маг-

нитную проницаемость µ

, вторая – µ

Найти

B во всем пространстве.

5.4. Ток J течет по прямолинейному проводу, совпадающему с осью

Z. От оси расходятся веерообразно три полуплоскости, образующие

три двугранных угла α

, α

(α

+ α

= 2π). Простран-

ство внутри каждого из углов заполнено однородным магнетиком с

магнитными проницаемостями соответственно µ

, µ

. Определить

магнитное поле во всём пространстве.

5.5. Найти магнитное поле в тонкой плоской щели, если поле в сре-

де (µ) можно считать однородным.

5.6. Бесконечный прямолинейный провод радиуса a с магнитной

проницаемостью µ

находится во внешнем однородном поперечном

магнитном поле

в среде с магнитной проницаемостью µ

. По про-

5.1 Граничные условия для магнитного поля. Метод изображений. Постоянные магниты. Магнитные цепи

129

воду течет постоянный ток J. Найти векторный потенциал и магнит-

ное поле во всем пространстве.

5.7. В однородное магнитное поле

вносится шар радиуса a с маг-

нитной проницаемостью µ

. Определить результирующее поде, инду-

цированный магнитный момент шара ~m и плотность токов

мол

, экви-

валентных приобретаемой шаром намагниченности. Магнитная про-

ницаемость окружающей среды µ

5.8. Найти магнитное поле в сферической полости радиуса a, нахо-

дящейся во внешнем однородном магнитном поле. Магнитная прони-

цаемость среды, окружающей полость, равна µ.

5.9. Равномерно намагниченная сфера (идеализированный ферро-

магнетик) вносится во внешнее однородное магнитное поле

. Най-

ти результирующее магнитное поле. Магнитная проницаемость сферы

, окружающей среды µ

5.10. Решить задачу 5.7, если шар, вносимый в поле, сверхпрово-

дящий.

5.11. В однородное магнитное поле

H помещена сверхпроводящая

сферическая оболочка радиуса R. Найти силу, приложенную к каждой

из симметричных полусфер.

5.12. Бесконечно длинная полая цилиндрическая оболочка с ради-

усами a и b (a < b) находится во внешнем однородном магнитном

поле

, перпендикулярном ее оси. Магнитная проницаемость цилин-

дра – µ

, окружающего пространства – µ

. Найти поле в полости.

Рассмотреть частный случай µ

 µ

5.13. Контур с током лежит в плоскости раздела двух сред с про-

ницаемостями µ

и µ

. Определить магнитное поле во воем простран-

стве, считая известным поле H

, создаваемое этим контуром в вакуу-

ме.

5.14. Бесконечный прямой провод с током J расположен парал-

лельно плоской границе раздела двух сред с магнитными проницае-

мостями µ

и µ

(провод – в среде с µ

). Расстояние от провода до