Медведев Г.А. Математические модели финансовых рисков. Часть 1
Подождите немного. Документ загружается.


57
() ()
(
)
()
()
()
()
Srtdt Srtdt
rt
t
Stdt
j
j
n
j
n
j
j
j
n
j
n
=-
==
-
=
-
ååå
11
1
1
1
s
s
()
()
()
()
()
()
.
1
1
dtt
t
tr
trS
n
j
j
n
j
ú
ú
û
ù
ê
ê
ë
é
÷
÷
ø
ö
ç
ç
è
æ
-=
å
-
=
s
s
()
()
()
()
()
()
()
()
St
t
t
tdt
j
j
n
n
j
j
n
m
m
s
s-
æ
è
ç
ç
ö
ø
÷
÷
é
ë
ê
ê
ù
û
ú
ú
=
-
å
1
1
()
()
()
()
()
()
.
1
1
dtt
t
tr
trS
n
j
j
n
j
ú
ú
û
ù
ê
ê
ë
é
÷
÷
ø
ö
ç
ç
è
æ
-=
å
-
=
s
s
()
()
()
()
()
()
()
() ()
()
()
()
()
()
St
t
t
trt
rt
t
tdt
j
j
n
n
j
n
j
j
n
m
m
s
s
s
s--+
æ
è
ç
ç
ö
ø
÷
÷
é
ë
ê
ê
ù
û
ú
ú
=
=
-
å
1
1
()
()
()
() ()
()
()
()
() ()
()
()
=
-
-
-
æ
è
ç
ç
ö
ø
÷
÷
é
ë
ê
ê
ù
û
ú
ú
=
=
-
å
St
trt
t
trt
t
dt
j
j
j
j
n
n
j
n
s
m
s
m
s
1
1
0
()
(
)
(
)
()
()
()
(
)
(
)
()
()
,
t
trt
t
trt
n
n
j
j
s
m
s
m -
=
-
На рынке будут отсутствовать условия арбитража только тогда, когда, каким
бы ни выбирал инвестор распределение {S
j
} своих денег по типам
приобретаемых ценных бумаг для получения безрисковой прибыли,
приращение суммы S(t) будет в точности равным приращению безрискового
актива такой же стоимости, то есть должно выполняться равенство
dS(t) = S(t) r(t) dt =
=
=
Приравнивая полученные формулы для безрискового приращения стоимости
S(t), приходим к равенству
Откуда
.
Поскольку это равенство должно выполняться для любого распределения
{S
j
, 1 £ j £ n} имеющейся суммы S{t} по типам ценных бумаг, мы приходим к
следующему условию отсутствия безрискового арбитража:
1 £ j £ n - 1.
Таким образом, отношение превышения средней доходности m
(j)
(t)
ценной бумаги с датой погашения Т
j
над краткосрочной процентной ставкой

58
() ( )
¶
¶
P
t
rtPtT
-=,0
()
()
dP t T
PtT
,
,
=
() () ()
~
,,expPtT PtT rsds
t
=-
é
ë
ê
ù
û
ú
ò
0
() () () () ()
dP t T dP t T r s ds P t T d r s ds
tt
~
, , exp , exp
=-
é
ë
ê
ù
û
ú
--
é
ë
ê
ù
û
ú
ì
í
ï
î
ï
ü
ý
ï
þ
ï
=
òò
00
() ( ) () () () ( ) ()
=- -
é
ë
ê
ù
û
ú
=-
ò
ss
T
t
T
t P t T r s ds dW t t P t T dW t,exp
~
,
0
(
)
~
,PtT
()
[]
()
EPTT PtT
t
~
,
~
,=
() () ()
~
,,expPtT PtT rsds
t
=-
é
ë
ê
ù
û
ú
ò
0
() ()
~
,expPTT rsds
T
=-
é
ë
ê
ù
û
ú
ò
0
() ( ) ()
ErsdsPtTrsds
t
Tt
exp , exp-
é
ë
ê
ù
û
ú
ì
í
ï
î
ï
ü
ý
ï
þ
ï
=-
é
ë
ê
ù
û
ú
òò
00
r(t) к волатильности s
(j)
(t) процесса изменения доходности этой ценной
бумаги при отсутствии безрискового арбитража не должно зависеть от даты
погашения и должно быть одинаковым для всех дат погашения. Оно и
называется рыночной ценой риска l(r(t),t).
Заметим, что в детерминированном случае, когда s
Т
(t) º 0 для всех t ³ 0,
мы имеем из уравнения (2.34)
dР(t,Т) = r(t)Р(t,Т) dt или
что совпадает с уравнением (1.5).
Для случая l(r,t) º 0 мы получаем из уравнения (2.34)
r(t) dt – s
Т
(t) dW(t).
Обозначив
, получим
.
Поскольку цена
является процессом Ито с нулевым дрейфом, она
является мартингалом и, следовательно,
.
Замечая, что
, а Р(Т,Т) = 1, мы получаем
и
.

59
() ()
PtT E rsds
t
t
T
,exp=-
é
ë
ê
ù
û
ú
ì
í
ï
î
ï
ü
ý
ï
þ
ï
ò
()
~
rt
r
,
~
r
()
~
rt
()
~
rs
() ()
PtT E r sds
t
Q
t
T
,exp
~
=-
é
ë
ê
ù
û
ú
ì
í
ï
î
ï
ü
ý
ï
þ
ï
ò
()
~
rs
()
~
rt
Таким образом,
. (2.35)
Для случая, когда l(r, t) ¹ 0 , наряду с краткосрочной процентной ставкой
r(t) рассмотрим процентную ставку
= m
Т
(t) + l(r, t)s
Т
(t), которая
называется процентной ставкой, отрегулированной риском (risk-adjusted
interest rate), и удовлетворяет стохастическому дифференциальному уравнению
d
~
(s) = (m
Т
(s) + l( s)s
Т
(s)) ds + s
Т
(s) dW(s) , s ³ t , = r(t). (2.36)
Тогда, согласно уравнению (2.34) для цены облигации, мы будем имеем ту же
самую формулу (2.35), в которой вместо краткосрочной процентной ставки
r(s), s ³ t , используется отрегулированная риском процентная ставка
и
условное математическое ожидание берется не по исходной вероятностной
мере, а по модифицированной вероятностной мере Q (risk adjusted probability
measure), согласованной с уравнением (2.36), т. е.
.
В этом случае (2.36) обычно называется уравнением Q-динамики. Заметим, что
поведение процентной ставки
для s ³ t зависит от ее исходного значения
= r(t), так что значение r(t) = r наряду с t тоже является параметром,
определяющим цену облигации. В этом смысле цена может рассматриваться
как функция трех переменных Р(t, r, Т).
ОДНОФАКТОРНЫЕ МОДЕЛИ КРАТКОСРОЧНЫХ СТАВОК
В этом классе моделей временной структуры снова в качестве
математической модели изменений краткосрочной ставки выбирается процесс с
независимыми приращениями. Предполагая, что Р(t, r, Т) является
детерминированной функцией краткосрочной ставки r = r(t) в момент t, из
условия отсутствия арбитража можно, как и прежде, получить
дифференциальное уравнение в частных производных для Р(t,Т). В этих
моделях предполагается, что изменения краткосрочной ставки r(t)
описываются процессом Ито
dr(t) = m(r(t), t) dt + s(r(t), t) dW(t),

60
()
[]
() () ()
.
2
1
2
2
2
tdW
r
P
tdt
t
P
r
P
t
r
P
tdP
rrr
¶
¶
s
¶
¶
¶
¶
m
¶
¶
s +
þ
ý
ü
î
í
ì
++=
()
[]
() ()
()
dP
P
t
P
r
t
P
r
P
t
P
dt
t
P
r
P
dW t
rr r
=
++
+
1
2
2
2
2
s
¶
¶
m
¶
¶
¶
¶
s
¶
¶
()
()
[]
()
m
s
¶
¶
m
¶
¶
¶
¶
T
rr
t
t
P
r
t
P
r
P
t
P
=
++
1
2
2
2
2
()
()
s
s
¶
¶
T
r
t
t
P
r
P
=-
()
[]
()
()
()
1
2
2
2
2
s
¶
¶
m
¶
¶
¶
¶
l
s
¶
¶
rr r
t
P
r
t
P
r
P
t
P
rrt
t
P
r
P
++
=-
,
где m (r(t), t) и s(r(t), t) являются соответственно дрейфом и волатильностью
процесса r(t) в момент t. Для простоты мы будем пользоваться символами
m
r
(t) и s
r
(t) вместо m (r(t), t) и s(r(t), t). Тогда
dr(t) = m
r
(t) dt + s
r
(t) dW(t) . (2.37)
Примером такой модели является уже рассмотренная модель Васичека.
Поскольку краткосрочная ставка {r(t)} представляет собой процесс с
независимыми приращениями, из леммы Ито следует, что для каждого Т ³ 0
процесс цен {Р(t, r(t), Т), 0 £ t £ Т} сам является процессом с независимыми
приращениями и инфинитезимальное приращение Р = Р(t, r(t), Т) в момент t
дается выражением
Таким образом,
.
Сравнивая это с уравнением (2.30), мы получим
и
.
Подставив последние два выражения в условие отсутствия арбитража (2.33),
получаем
,
или

61
()
[]
() ( ) ()
[]
1
2
0
2
2
2
s
¶
¶
mls
¶
¶
¶
¶
rrr
t
P
r
trtt
P
r
P
t
rP++ +-=,
()
B
e
k
k
t
t
=
-
-
1
()
()
[]
()
()
[]
A
Bkk
k
B
k
t
tt qls
s
ts
=
-+-
é
ë
ê
ù
û
ú
-
2
2
2
2
2
4
. (2.38)
Как мы заметили выше, уравнение (2.38) справедливо для любых ценных
бумаг или портфелей, чьи процессы цен подчиняются уравнению (2.30).
Уравнение (2.38) полностью совпадает с уравнением временной структуры
(2.14). Иногда оно называется фундаментальным дифференциальным
уравнением в частных производных для определения цен активов. Оно
обеспечивает общую структуру для вычисления цены дисконтируемых
облигаций в моделях краткосрочной ставки.
Когда решение уравнения (2.38) может быть представлено в виде
Р(t, r,Т) = ехр{А(t,Т) - r В(t,Т)} , (2.39)
говорят, что модель обладает аффинной временной структурой (affine term
structure). Для того чтобы цена актива (2.39) удовлетворяла условию погашения
Р(Т, r, Т) = 1, необходимо, чтобы для любого значения краткосрочной
процентной ставки r имели место равенства А(Т, Т) = 0, В(Т, Т) = 0. Модели с
аффинной временной структурой составляют класс аффинной доходности
(affine yield class). Рассмотрим основные модели этого класса.
К классу аффинной доходности принадлежит рассмотренная в разделе 2.1
модель Васичека, в которой волатильность и дрейф процесса в уравнении
краткосрочной ставки (2.37) определяются так: s
r
(t) является константой, а
m
r
(t) = k(q – r(t)) , где k и q постоянные. Предполагается также, что рыночная
цена риска не зависит от времени и величины краткосрочной процентной
ставки, т. е. l(r,t) = l, где l является постоянной. Функции А(t,Т) и В(t,Т) для
этой модели имеют вид
, t = Т - t,
и
.
Доказательство. Из выражения (2.39), которое при постоянных
коэффициентах приобретает вид Р(t, r, Т) = ехр{А(t) - r В(t)}, мы имеем
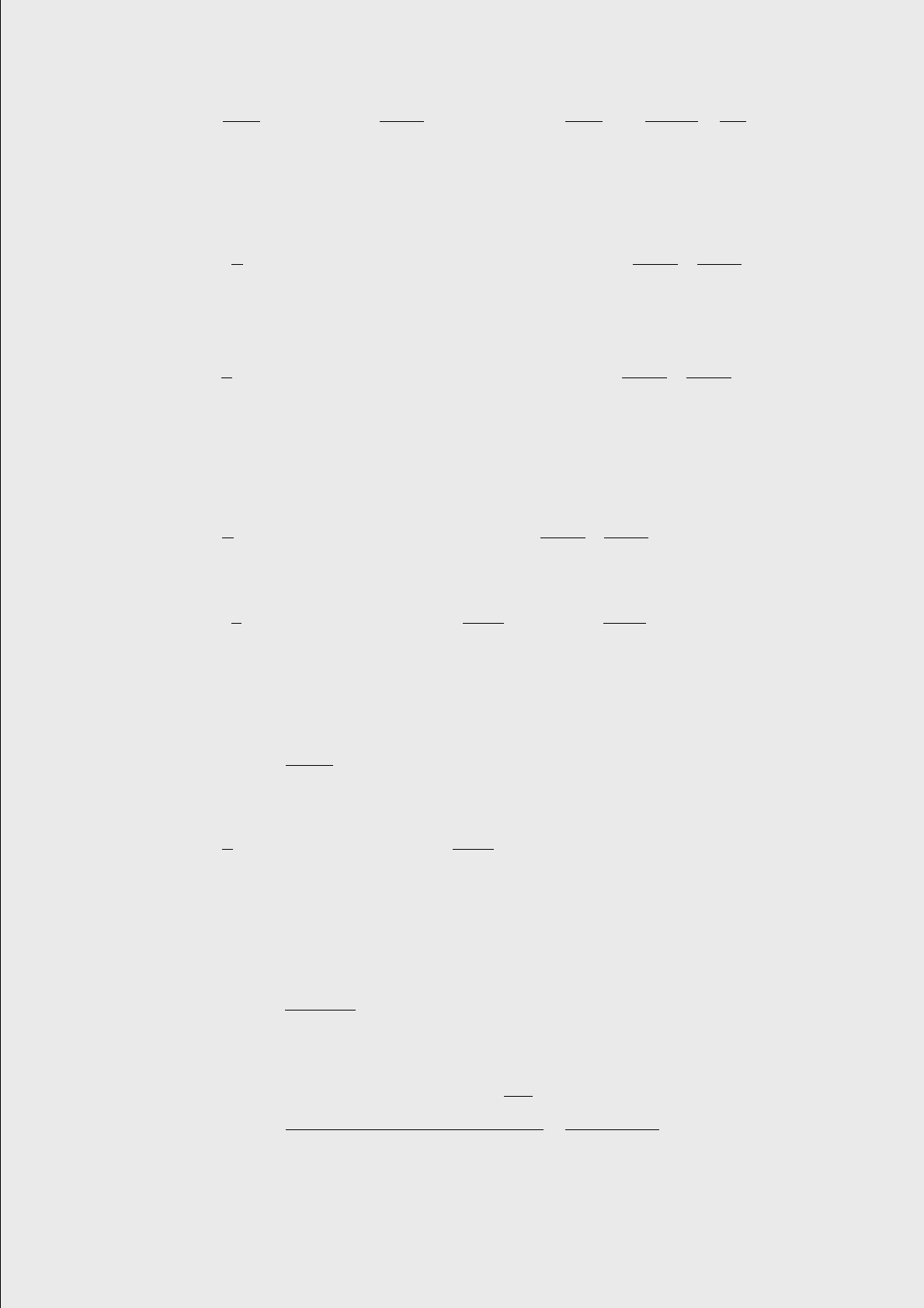
62
()
¶
¶
t
P
r
BP
=-
()
¶
¶
t
2
2
2
P
r
BP=
()
¶
¶
t
tt
P
t
r
dB
d
dA
d
P
=-
é
ë
ê
ù
û
ú
()
[]
()
[]
() ( ) ()
[]
()
()
()
1
2
0
22
stmlst
t
t
t
t
rrr
tB t rt tB rr
dB
d
dA
d
P-+ -+ -
ì
í
î
ü
ý
þ
=,
()
[]
()
[]
() ( ) ()
[]
()
()
()
1
2
0
22
stmlst
t
t
t
t
rrr
tB t rt tB rr
dB
d
dA
d
-+ -+ -=,
()
[]
()
[]
()
()
()
1
2
0
2
2
st q lst
t
t
t
t
BkrBrr
dB
d
dA
d
--+ -+ - =
()
[]
[]
()
()
()
()
1
2
10
2
2
st qlst
t
t
t
t
t
BkB
dA
d
rkB
dB
d
-+ -
ì
í
î
ü
ý
þ
++-
é
ë
ê
ù
û
ú
=
()
()
kB
dB
d
t
t
t
+-=10
()
[]
[]
()
()
1
2
0
2
2
st qlst
t
t
BkB
dA
d
-+ - =
()
B
e
k
k
t
t
=
-
-
1
()
()
[]
()
()
[]
A
Bkk
k
B
k
t
tt qls
s
ts
=
-+-
é
ë
ê
ù
û
ú
-
2
2
2
2
2
4
, и .
Подстановка этих производных в уравнение (2.38) дает
,
или
. (2.40)
Для модели Васичека m
r
(t) = k(q – r(t)) и s
r
(t) = s. Выбирая l(r, t) = l,
получаем равенство (2.40) в виде
,
или
.
Так как это уравнение справедливо для любых r, мы имеем
, В(0) = 0,
и
, А(0) = 0.
Решая эти уравнения относительно А и В (о решении дифференциальных
уравнений см. математическое дополнение), мы получаем
и
.
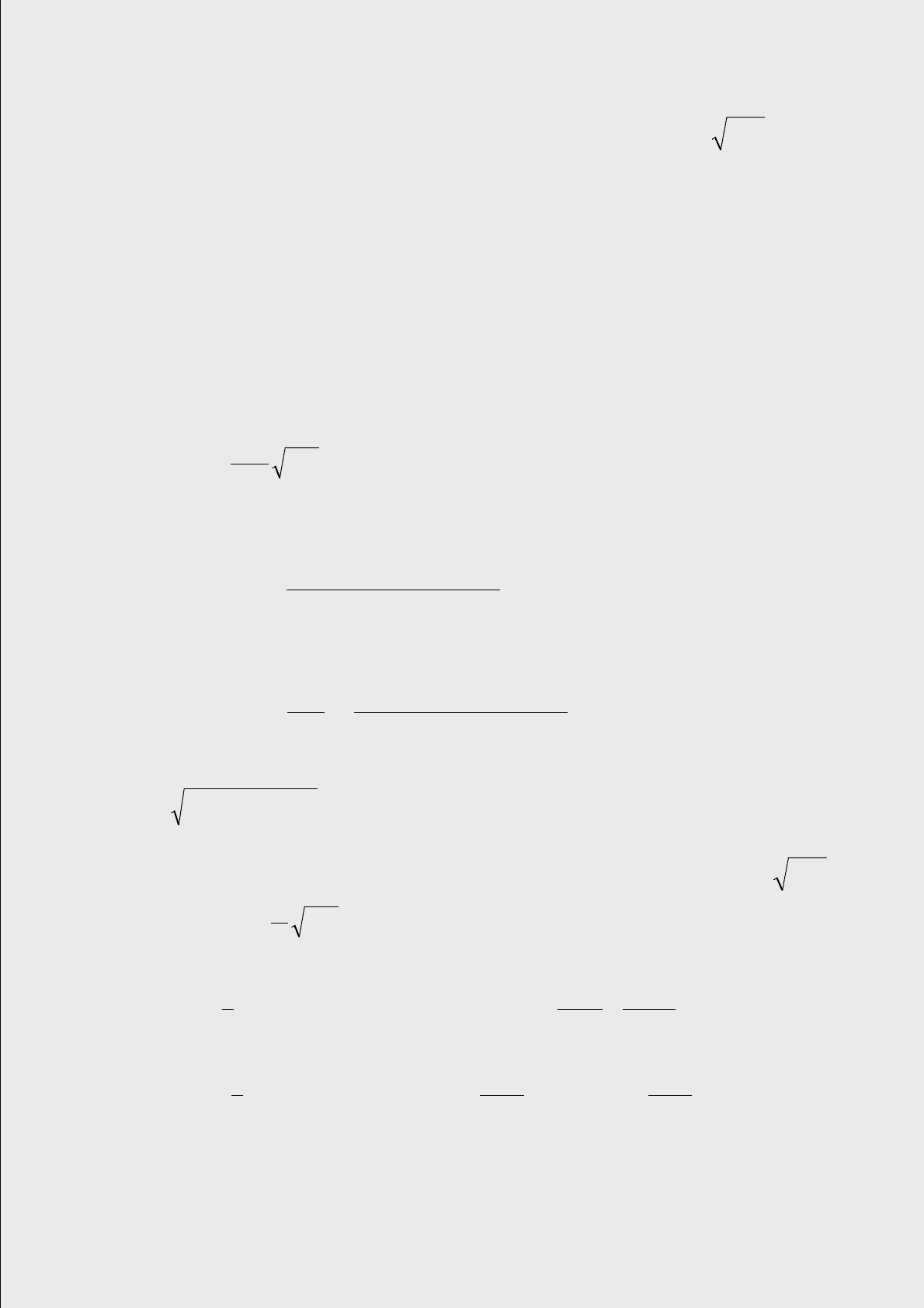
63
(
)
rt
()
()
-
l
s
t
rt
()
()
()
()
B
e
ke
t
ele
et
et
=
-
+++ -
21
21
()
()
()
()
A
k
e
ke
k
t
q
s
e
ele
let
et
=
+++ -
é
ë
ê
ê
ê
ù
û
ú
ú
ú
++
2
2
21
2
2
ln
/
()
s=++k
2
2
2
(
)
rt
()
-
l
s
rt
()
[]
()
[]
()
()
()
1
2
0
2
2
st q lt
t
t
t
t
rB k r rB r r
dB
d
dA
d
--- -+ - =
()
[]
[]
()
()
()
()
1
2
10
2
2
st lt
t
t
qt
t
t
BkB
dB
d
rkB
dA
d
++ -+
ì
í
î
ü
ý
þ
-+
é
ë
ê
ù
û
ú
=
Другой моделью класса аффинной доходности является модель CIR (Cox,
Ingersoll & Ross, 1985), для которой m
r
(t) = k(q – r(t)) и s
r
(t) = s , где k,
s и q являются постоянными. Заметим, что при заданных таким образом
параметрах уравнение краткосрочной процентной ставки (2.37) определяет
случайный процесс r(t) с отражающей границей r(t) = 0. Это значит, что если в
некоторый исходный момент времени t = 0 процентная ставка r(0) была
положительной, то она остается положительной в течение всего последующего
времени. Это обеспечивает с практической точки зрения адекватную ситуацию,
так как реальные процентные ставки всегда являются неотрицательными.
(Кстати, этого не обеспечивает модель Васичека, так как в ней с положительной
вероятностью процентные ставки могут быть отрицательными.) В модели CIR
рыночная цена риска устанавливается путем использования модели рыночного
равновесия в общей трактовке. Рыночная цена риска l(r, t) задается
выражением
. Чтобы получить явный вид решения для модели CIR,
предположим, что l(t) является постоянной l, тогда
и
,
где
el , t = Т - t.
Доказательство. Для модели CIR m
r
(t) = k(q – r(t)) и s
r
(t) = s .
Выбирая l(r,t) =
, мы получаем выражение (2.40) в виде
,
или
.
Снова пользуясь тем, что это равенство справедливо для любых r , получаем
следующие уравнения для А и В:
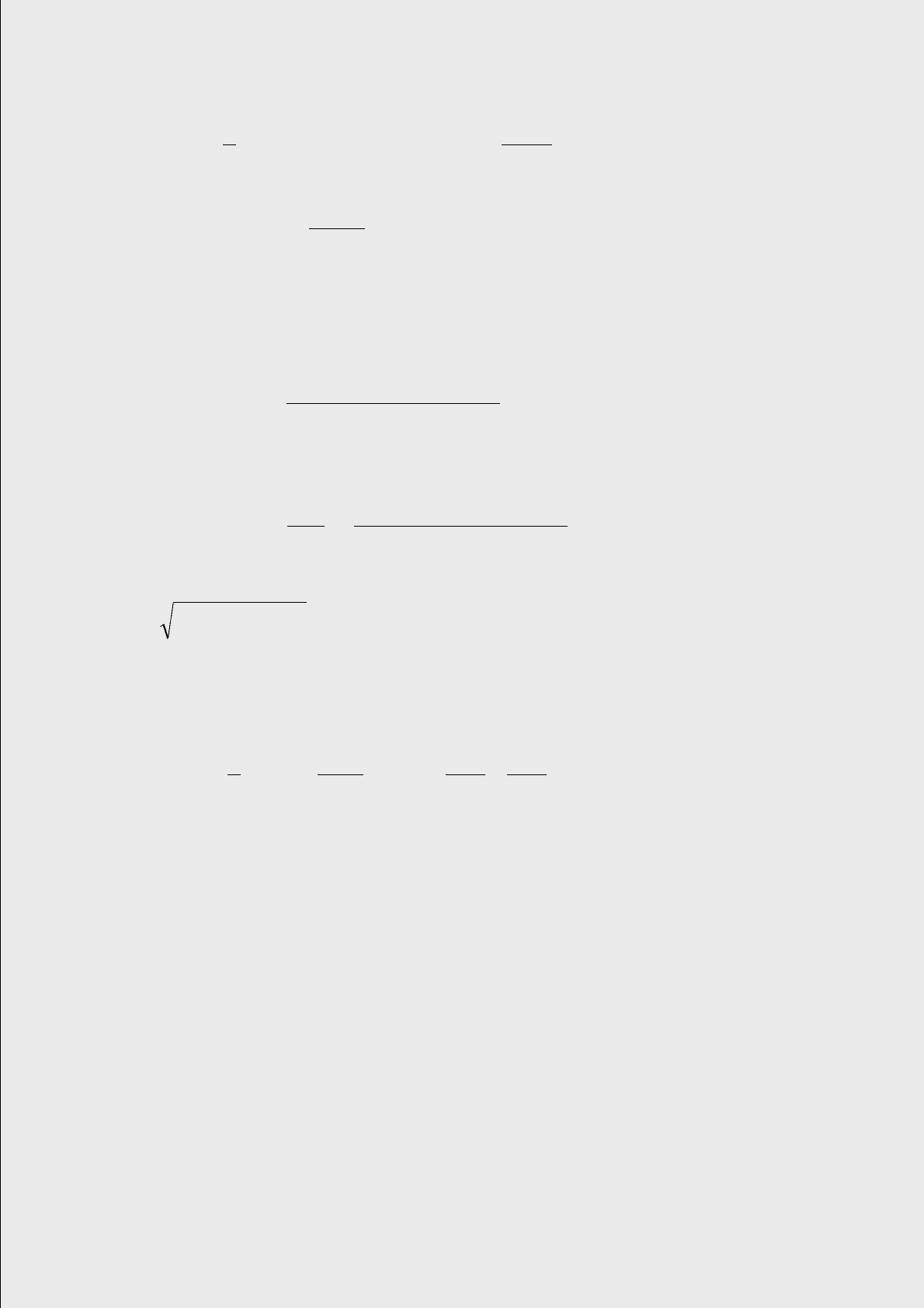
64
()
[]
[]
()
()
1
2
10
2
2
st lt
t
t
BkB
dB
d
++ -+ =
()
()
kB
dA
d
qt
t
t
+=0
()
()
()
()
B
e
ke
t
ele
et
et
=
-
+++ -
21
21
()
()
()
()
A
k
e
ke
k
t
q
s
e
ele
let
et
=
+++ -
é
ë
ê
ê
ê
ù
û
ú
ú
ú
++
2
2
21
2
2
ln
/
()
s=++k
2
2
2
()
[]
()
[]
1
2
0
2
2
2
s
¶
¶
m
¶
¶
¶
¶
rr
t
P
r
t
P
r
P
t
rP++-=
~
~
m
r
, В(0) = 0,
и
, А(0) = 0.
Решая эти уравнения относительно А и В (о решении дифференциальных
уравнений см. математическое дополнение), мы получаем
и
,
где
el .
Модель CIR и модель Васичека являются частными случаями более общей
модели МС (Medvedev & Cox, 1996), для которой уравнение временной
структуры (2.38) может быть записано в форме
, (2.41)
где отрегулированный риском дрейф
= m
r
(t) + l(r,t)s
r
(t) и квадрат
волатильности s
r
2
явно не зависят от времени, что относит ее к классу
моделей, однородных по времени (time homogeneous model), и являются
линейными функциями краткосрочной процентной ставки (что обеспечивает
аффинность модели), т. е.
m
r
(t) = a r + b, s
r
2
(t) = g r + d, l(r, t)s
r
(t) = x r + h, (2.42)
где a , b , g , d , x и h являются константами, которые удовлетворяют
определенным ограничениям.
Перечислим вкратце эти ограничения. Для того чтобы процесс
краткосрочной процентной ставки был устойчивым (т. е. с течением времени
дисперсия процесса не увеличивалась неограниченно, а устанавливалась на
некотором уровне), необходимо, чтобы a < 0 . При этом среднее значение
краткосрочной процентной ставки будет устанавливаться к уровню -b /a,

65
()
()
()
B
e
e
t
eJ
et
et
=
-
+-
21
21
()
x g=++
2
2
() ()
()
()
()
AB
dB
d
t
d
g
tt
w
g
axt
t
t
=- - ++
æ
è
ç
ö
ø
÷
é
ë
ê
ù
û
ú
2
ln
(
)
()
ax gbh=+-+
(
)
Je ax=- +
когда t ® ¥. Из соотношений (2.42) также вытекает необходимое условие
s
r
2
(t) = g r + d ³ 0. Смысл его состоит в следующем. Сделаем естественные
предположения, что исходное значение краткосрочной процентной ставки r(0)
было таким, чтобы это условие выполнялось, g r + d ³ 0, и что это неравенство
выполняется строго при установившемся значении краткосрочной процентной
ставки r = -b /a, т.е. d - bg /a > 0. Тогда из свойств стохастического
уравнения (2.37) следует, что с течением времени это условие будет
удовлетворяться всегда. Физически это означает, что значение r = - d / g
является отражающей границей процесса краткосрочной процентной ставки.
Когда процесс r(t) достигает этого уровня, мгновенная волатильность
процесса s
r
(t) обращается в нуль, уравнение (2.37) перестает быть
стохастическим и начинает детерминированно изменяться в сторону своего
уровня установления, т. е. удаляется от этой границы внутрь области, где
выполняется условие g r + d > 0.
Модель МС превращается в модель Васичека, когда
m
r
(t) = a r + b = k (q – r), т. е. a = - k, b = k q.
s
r
2
(t) = g r + d = s
2
, т. е. g = 0, d = s
2
.
l(r, t)s
r
(t) = x r + h = ls , т. е. x = 0, h = ls .
Заметим, что в модели Васичека отражающая граница процесса краткосрочной
процентной ставки удаляется к - ¥ .
Модель МС превращается в CIR модель, когда
m
r
(t) = a r + b = k (q – r), т. е. a = - k, b = k q.
s
r
2
(t) = g r + d = s
2
r, т. е. g = s
2
, d = 0.
l(r,t)s
r
(t) = x r + h = -l r, т. е. x = - l, h = 0.
В модели CIR отражающей границей процесса краткосрочной процентной
ставки является r = - d / g = 0.
Для модели МС функции А(t) и В(t) имеют вид
, ea
и (2.43)
.
где для компактности использованы обозначения
wd ,
.

66
()
()
[]
()
[]
()
()
()
1
2
0
2
gdt axbht
t
t
t
t
rB r Brr
dB
d
dA
d
+ -+++ -+ - =
()
() ()
dB
d
BB
t
ax t g t=+ - +
1
2
1
2
()() ()
dA
d
BB
t
bh t d t=- + +
1
2
2
()
() ( ) ()
.
5,01
2
t
txatg
t
d
BB
dB
=
++-
(
)
(
)
() ( )
()
()
.lnln
1
t
exa
exa
exatg
exatg
e
=
÷
÷
ø
ö
ç
ç
è
æ
++
-+
-
-+-
++-
B
B
() ( ) () ()
.
2
1
0
2
ttdthbt
t
dBBA
ò
ú
û
ù
ê
ë
é
-+=
Доказательство. Для модели МС уравнение (2.40) приобретает вид
.
Оно распадается на два уравнения:
, В(0) = 0,
и
, А(0) = 0.
Обращаясь к математическому дополнению в конце книги, можно решить
эти уравнения и получить выражения (2.43). Однако наряду с этим мы
используем несколько другой способ. Заметим, что уравнение для В(t) можно
записать в виде
Это равенство можно проинтегрировать по интервалу (0,t) , так как в левой
части стоит интеграл от рациональной функции, который берется в явной
форме. Поскольку (a + x)
2
+ 2g = e
2
> 0, с учетом того, что В(0) = 0,
интегрирование дает
Определяя отсюда В(t) , находим требуемое выражение. Для получения А(t)
заметим, что второе уравнение является просто производной от этой функции.
Поэтому его достаточно проинтегрировать по интервалу (0,t), чтобы получить
выражение для А(t) , учитывая, что А(0) = 0. Так что
Этот интеграл можно переписать с учетом предыдущего интегрирования как
