Медведев Г.А. Математические модели финансовых рисков. Часть 1
Подождите немного. Документ загружается.


214
YcWB
iit
t
t
+-
=
¥
=
å
1
0
()
()
DctrH trEE B B
mn kn
Ttl
T
tk
tkll
m
k
m
=+
ì
í
ï
î
ï
ü
ý
ï
þ
ï
é
ë
ê
ê
ù
û
ú
ú
-
--
=
¥
==
ååå
2
0
11
ln
max ,
{}{}
-+
é
ë
ê
ù
û
ú
+- +-
==
åå
c trE H trE H
kn n k l
TT
nl
l
m
k
m
2
1
11
ln
HE HE HE H
jk kn
k
j
jn
T
kn
kj
m
nj-
=
-
=+
+-
åå
++ =
1
1
0
1
1
HHB
k
k
=
0
относительно матриц Е
kn .
Вид уравнений (1) и (4) гарантирует, что математи-
ческое ожидание вектора ошибок равно нулю, то есть Е[DY
i+n
] = 0 .
Из уравнения (1) следует, что при выполнении условия стационарности
процесса
. (6)
Используя представление (6) в соотношениях (1) и (4), мы можем получить
формулу для суммы дисперсий D
тn
в виде
. (7)
Здесь trН обозначает след матрицы Н . Матрицы Н были введены равенст-
вом (3). Заметим, что из представления (6) следует, что матрицы Н
k
связаны с
кросс-корреляционными матрицами соотношениями
Соv(Y
i
,Y
i
) = с
2
Н
0
и Соv(Y
i
,Y
i+ k
) = с
2
Н
k
.
Поскольку выражение (7) является выпуклой функцией относительно элемен-
тов матрицы Е
kn
, сумма дисперсий D
тn
имеет единственный минимум на
множестве матриц Е
kn
. Дифференцирование D
тn
по элементам матрицы Е
kn
и
приравнивание к нулю производных дает систему уравнений для матрицы Е
kn
в
виде
, 1 £ j £ т . (8)
Единственный минимум функции (7) гарантирует существование единственно-
го решения системы (8). Это решение является очень простым:
Е
1n
= В
n
, Е
kn
= 0 , 1 £ k £ т . (9)
Действительно, оно следует из определения (3), где
. Слагаемое с
Е
1n
в левой части уравнения (8) равно Н
j-1
Е
1n
, а правая часть уравнения равна
Н
n+j-1
= Н
j-1
В
n
. Система уравнений (8) будет удовлетворяться, если мы выбе-
рем решение с помощью равенств (9). Из-за единственности решения никаких
других решений не существует.

215
$
in+
$
Y
in+
D
mn
opt
()
c
qN
tr Y Y Y Y B
it
T
it
t
N
it
T
it
t
N
2
11
1
1
21
2
1
1
=
-
-
ì
í
î
ü
ý
þ
+- +-
=
-
+- +-
=
åå
U
YY YY
YY YY
N
itN
T
itN
t
N
itN
T
it N
t
N
it N
T
itN
t
N
it N
T
it N
t
N
=
æ
è
ç
ç
ç
ç
ö
ø
÷
÷
÷
÷
+- +-
=
-
+- +--
=
-
+-- +-
=
-
+-- +--
=
-
-
åå
åå
2
1
1
2
1
1
2
1
11
2
1
1
V
YY
YY
N
itN
T
it N
t
N
it N
T
it N
t
N
=
æ
è
ç
ç
ç
ç
ö
ø
÷
÷
÷
÷
+- ++-
=
-
+-- ++-
=
-
å
å
1
2
1
11
2
1
Таким образом, для матричной марковской модели оптимальная оценка
предсказания
Y использует только последнее наблюдение Y
i
для предска-
зания вектора Y
i+n
:
= Y
i
В
n
, (10)
где матрица В вычисляется по формуле (2). Подставляя решение системы (8) в
выражение (7) для суммы дисперсий D
тn
, мы получим значение, которое дает
суммарную среднеквадратическую точность оценки предсказания (10):
= с
2
tr{Н
0
[I - (В
n
)(В
n
)
Т
]} , (11)
где I является единичной матрицей. Оценка параметра с
2
может быть найдена
путем подстановки представления (2) в выражение (1) вместо матрицы В . Ос-
тавляя детали для более сложного случая, рассмотренного ниже, мы запишем
выражение несмещенной оценки параметра с
2
для марковской модели:
,
где tr{А} обозначает след матрицы А , а В вычисляется по формуле (2).
АВТОРЕГРЕССИОННЫЕ МОДЕЛИ БОЛЕЕ ВЫСОКИХ ПОРЯДКОВ
Анализ матричных моделей в виде авторегрессий более высокого порядка
является более сложным. Например, рассмотрим случай второго порядка, когда
процесс Y
i
описывается уравнением
Y
i+1
= Y
i
В
1
+ Y
i-1
В
2
+ сW
i
. (12)
Введем для краткости следующие обозначения
,
.
216
B
B
UV
NN
1
2
æ
è
ç
ö
ø
÷
=
() ( )
()()
()
()
B
B
Cov Y Y Cov Y Y
Cov Y Y Cov Y Y
Cov Y Y
Cov Y Y
tt tt
tt tt
tt
tt
1
2
1
1
1
1
11
æ
è
ç
ö
ø
÷
=
æ
è
ç
ö
ø
÷
æ
è
ç
ö
ø
÷
-
-
-
+
-+
,,
,,
,
,
()
cJ
N
YY BBU
B
B
NitN
T
it N
t
N
TT
N
2
11
2
1
12
1
1
2
1
2
=
-
-
æ
è
ç
ö
ø
÷
é
ë
ê
ù
û
ú
++- ++-
=
-
-
å
J
N
WW
NitN
T
itN
t
N
=
-
+- +-
=
-
å
1
2
2
1
()
J
N
WW
N
uv
tu tv
t
N
=
-
=
-
å
1
2
2
1
()
c
qN
YY VUV
it N
T
it N
t
N
N
T
NN
2
11
2
1
1
2
=
-
-
é
ë
ê
ù
û
ú
++- ++-
=
-
å
Тогда оценка максимального правдоподобия матриц В
1
и В
2
может быть за-
писана в виде
.
Заметим, что в рассматриваемом случае также, как и для описанной выше мар-
ковской модели, с вероятностью 1 имеет место следующее предельное соотно-
шение при N ® ¥ :
.
Для кросс-корреляционной матрицы при различных индексах справедливо ра-
венство
Соv(Y
t+k
, Y
t
) = Соv(Y
t
, Y
t+k
)
Т
.
Если процесс Y
t
является стационарным, то матрица Соv(Y
t
, Y
t+k
) не зависит
от значения индекса t .
Используя это представление в соотношении (12) можно получить равен-
ство
,
где через
обозначена (q´q) - матрица с элемента-
ми
, а {W
tи
} являются нормальными случайными ве-
личинами с нулевыми математическими ожиданиями, которые взаимно незави-
симы и имеют одинаковую дисперсию, равную единице. Поэтому из закона
больших чисел следует, что
(J
N
)
ии
® 1 , (J
N
)
иv
® 0 , и ¹ v , при N ® ¥ .
Таким образом, несмещенную оценку величины с
2
можно получить в виде
.

217
DF
t
t
t
=
¥
å
0
YcWDFcWF
ii
t
t
t
it t
t
+
=
¥
-
=
¥
==
åå
1
00
YcWF
iitt
t
+-
=
¥
=
å
1
0
YYBcW
iijj
j
p
i++-
=
=+
å
11
1
FFB
ttjj
j
p
++-
=
=
å
11
1
Пусть D обозначает диагональную матрицу с оператором временной задержки
на главной диагонали, то есть Y
t-1
= Y
t
D . Тогда рекуррентному соотношению
(12) можно придать вид
Y
i+1
(I - DВ
1
- D
2
В
2
) = сW
i
или Y
i+1
= сW
i
(I - DВ
1
- D
2
В
2
)
-1
. (13)
Теперь задачей является представление обратной матрицы, стоящей в правой
части, в виде полинома по операторам D . Предположим, что такое представ-
ление имеет вид
(I - DВ
1
- D
2
В
2
)
-1
= . (14)
Тогда мы имеем соотношение
(15)
вместо представления (6) и анализ является аналогичным марковскому случаю.
Аналитическими методами получить представление (15) очень трудно. Но
очень просто найти его алгоритмически. Действительно, используя уравнение
(12) как рекуррентное соотношение мы можем получить представление (15) в
виде
,
где матрицы F
t
вычисляются рекуррентно, а F
0
= I - единичная матрица,
F
1
= В
1
, F
t+1
= F
t
В
1
+ F
t-1
В
2
, t = 1, 2, ... . (16)
Заметим, что в авторегрессионной модели порядка р
(17)
представление (15) также возможно и в этом случае матрицы F
t
могут быть
вычислены по рекуррентной формуле
, t > 0 , F
0
= I , F
t
= 0 , t < 0 . (18)

218
(
)
$
min ,
Y c WFEc WFEcW FE
tn itk t
t
kn
k
m
it tk
tk
kn
k
m
it tk kn
k
tm
t
+--
=
¥
=
--
=
¥
=
--
==
¥
=
æ
è
ç
ö
ø
÷
=
æ
è
ç
ö
ø
÷
=
æ
è
ç
ö
ø
÷
åååååå
011 11
HFF
kt
T
tk
t
=
+
=
¥
å
0
$
in+
[]
()
EY Y cIE
HG
GG
I
E
in
T
in n
T
n
T
n
T
n
DD
++
=
-
-
æ
è
ç
ö
ø
÷
æ
è
ç
ö
ø
÷
2
0
()
EEEE
n
T
n
T
n
T
mn
T
=
12
...
()
GHH H
n
T
n
T
n
T
nm
T
=
++-11
...
EGG
n
opt
n
=
-1
Поэтому последующий анализ является справедливым для авторегрессионных
моделей произвольного порядка, то есть, по существу, мы будем рассматривать
модель (17) вместо модели (12).
Будем искать оценку предсказания тоже в виде (4). Тогда получим
.
(19)
Распространим обозначение (3) на произвольные матрицы F
t
, k = 0, 1, 2, ... . (20)
(Для модели (1) в этой формуле F
t
= В
t
.) Н
k
является (q´q) - матрицей. Из
формулы (15) следует, что
Соv(Y
t
, Y
t+k
) = с
2
Н
k
, Соv(Y
t+k
, Y
t
) = с
2
Н
k
Т
.
Матрица ковариации ошибки предсказания DY
i+n
= Y - Y
i+n
имеет вид
, (21)
где использованы обозначения:
- (q´qт) - матрица ко-
эффициентов предсказания;
- (q´qт)-матрица, со-
ставленная из матриц Н
k
Т
; G = (G
ij
) - (qт´qт)-матрица, составленная из
(q´q)-матричных блоков G
ij
, которые определяются следующими равенствами
G
ii
= Н
0
, G
ij
= Н
i-j
для i > j , G
ij
= Н
j-i
Т
для i < j . (22)
Главная диагональ корреляционной матрицы (21) составлена из дисперсий
ошибок предсказания компонент вектора Y
i+n
. Поэтому оптимальные матрицы
{Е
kn
} должны минимизировать след матрицы (21). Такие матрицы являются
решениями системы уравнений (8), где матрицы Н
k
определяются формулой
(17). Система (8) может быть записана с помощью принятых обозначений в
следующем виде: GЕ
n
= G
n
. Это означает, что оптимальные матрицы Е
kn
со-
ставляют матрицу
. (23)

219
E
n
opt
$
Y
in
opt
+
$
in
opt
+
GG
n
-1
E
n
opt
=
D
mn
opt
D
mn
opt
GG
n
-1
GG
n
-1
G
n
-1
G
n
-1
$
in+
Корреляционная матрица (21) для оптимальных матриц преобразуется к
виду
Е[(
- Y
i+n
)
Т
(Y - Y
i+n
)] = с
2
(Н
0
- G
n
Т
) . (24)
Заметим, что формула (18) справедлива для модели (1), поэтому формула (24)
для модели (1) справедлива тоже. Обозначения согласовываются при помощи
равенств
G
n
= Н
n
= Н
0
В
n
, G = Н
0
. (25)
Укажем на один важный частный случай, когда т = р , n = 1, когда спра-
ведливо равенство
(Е
11
Е
21
... Е
р1
)
Т
= (В
1
В
2
... В
р
)
Т
, которое следует из
того факта, что в этом частном случае матрицы {Е
k1
} и {В
k
} вычисляются по
одинаковым формулам через кросс-корреляционные матрицы. Этот факт явля-
ется важным, поскольку нет необходимости вычислять матрицы {F
k
} и {Н
k
}
по формулам (18) и (20), а достаточно использовать оценки матриц {В
k
} .
ВЫБОР ПАРАМЕТРА т ОЦЕНКИ ПРЕДСКАЗАНИЯ
Поскольку мерой оптимальности оценки предсказания является сумма
дисперсий компонент вектора ошибок предсказания, то есть след
корре-
ляционной матрицы (24), для общей модели мы имеем
= с
2
tr{Н
0
- G
n
Т
} = с
2
[tr{Н
0
} - tr{G
n
Т
}] =
= с
2
tr{Н
0
} [1- tr{G
n
Т
G }/tr{Н
0
}] . (26)
Величина
d
тn
= tr{G
n
Т
G }/tr{Н
0
} , 0 £ d
тn
£ 1 , (27)
определяет качество предсказания. Когда d
тn
= 0 , оценка предсказания имеет
ту же самую эффективность, что и тривиальное предсказание, то есть Y = 0
(отклонение предсказываемого вектора от среднего равно нулю). Чем больше
d
тn
, тем больше эффективность. Величина d
тn
может помочь выбрать пара-
метр т - число наблюдений, которые используются для конструирования
оценки (4). Действительно, если параметр т увеличить на единицу, то значе-
ние d
тn
увеличится до значения d
т+1, n
, так что
d
т+1, n
- d
тn
= tr{А
Т
ВА} / tr{Н
0
} ,
где символ А обозначает матрицу [Н(т)G
-1
G
n
- Н
n+т
] , В обозначает мат-
рицу [Н
0
- Н(т)G
-1
Н(т)
Т
]
-1
, Н(т) = [Н
т
Н
т-1
... Н
1
] - (q´qт) - матрица, со-

220
() ()
{}
AY uVarY AY uVarY
k i nk k i nk k i nk k i nk
+- ++
++++
$$
,
$$
,,,,aa
$
,
Y
ink+
$
,
Y
ink+
$
,ink+
$
,
Y
ink+
$
,ink+
E
n
opt
E
n
opt
ставленная из Н
k
, 1 £ k £ т . Приращение d
т+1, n
- d
тn
является неотрицатель-
ным, так как определяется следами неотрицательно определенной матрицы
(числитель) и положительно определенной матрицы (знаменатель). Если вели-
чина (d
т+1, n
- d
тn
)/d
тn
= О(1) или больше, тогда желательно использовать для
оценки предсказания (т + 1) наблюдений. Если же отношение (d
т+1, n
- d
тn
)/d
тn
оказывается очень малым по абсолютной величине, можно ограничиться только
т наблюдениями. Таким образом можно последовательно определить величи-
ну параметра т оценки предсказания (4). Как пример рассмотрим марковский
случай. Если т = 1, то G
n
= Н
n
= Н
0
В
n
, G = Н
0
. Н(т) = Н
1
= Н
0
В
. Тогда
Н(т)G
-1
G
n
- Н
n+т
= (Н
0
В)
Т
Н
0
-1
Н
0
В - Н
0
В
n+1
= 0 .
Это означает, что d
2
- d
1
= 0 и второе наблюдение не улучшает оценку пред-
сказания.
ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ
Модели (1), (12) и (17) являются линейными, оценка предсказания (4) -
тоже линейная. Поэтому ошибка оценки предсказания оказывается q-мерной
случайной величиной, которая имеет нормальное распределение с нулевым
средним и корреляционной матрицей (24). Это позволяет построить интерваль-
ные оценки в форме доверительных интервалов, которые обычно более инфор-
мативны, чем точечные оценки (4). Пусть уровни значимости a
k
заданы для
каждой компоненты оценки предсказания (4), 1 £ k £ q . Тогда доверительные
интервалы будут иметь вид
, (28)
где А
k
- среднее значение наблюдений k-й компоненты; - оценка пред-
сказания отклонения k-й компоненты от среднего значения; Vаr( ) - k-й
элемент главной диагонали корреляционной матрицы оценки
Y , которая
имеет вид
Соv(
,Y ) = с
2
( )
Т
G( ) . (29)
Оценка параметра с
2
дана выше; и
ak
- квантиль стандартного нормального
распределения на уровне (1 - a
k
/2) . Таким образом, предсказываемая k-я
компонента вектора доходности принадлежит интервалу (29) с вероятностью
(1 - a
k
) .

221
UYY
Nit
T
it
t
N
=
æ
è
ç
ö
ø
÷
+- +-
=
-
å
11
2
1
UYYYY U
UYYU
YU Y
Ni
T
iit
T
it
t
N
N
Ni
T
iN
iNi
T
++-+-
=
-
=+
æ
è
ç
ö
ø
÷
=-
+
å
111
2
1
1
BI
UYY
YU Y
B
UYY
YU Y
N
Ni
T
i
iNi
T
N
Ni
T
i
iNi
T
+
+
=-
+
æ
è
ç
ö
ø
÷+
+
1
1
11
()
$
$
YYB
YUY Y Y
YU Y
iiN
iNi
T
ii
iNi
T
++
+++
=+
-
+
21
111
1
РЕКУРРЕНТНАЯ ФОРМА ОЦЕНКИ
Иногда удобно после получения следующего (i + 1)-го наблюдения при по-
строении новой оценки предсказания использовать результаты предыдущих
вычислений. Когда вычисляется оценка предсказания, наиболее сложные рас-
четы связаны с вычислением матрицы U
N
, которые также могут быть и наиме-
нее точными. Можно предложить рекуррентный способ вычисления этой мат-
рицы после получения очередного наблюдения. Имеет место рекуррентная
формула, которую мы запишем для простоты в марковском случае,
.
.
Оценка максимального правдоподобия матрицы В
N+1
для N + 1 наблюдений
принимает вид
.
Используя это выражение, оценку предсказания (4) можно написать тоже в ре-
куррентной форме. Для n = 1 эта оценка принимает вид
.
Для модели (12) рекуррентная форма оценки матрицы В
Т
= (В
1
Т
В
2
Т
) и оценки
предсказания (4) будет аналогичной, если вместо Y
i
использовать (Y
i
Y
i-1
) ,
вместо Y
i+1
использовать (Y
i+1
Y
i
) и матрицу U
N
понимать так, как это опре-
деляется после формулы (12).
Пример. Рассмотрим данные для ставок доходности ценных бумаг Казна-
чейства США на ноябрь 1995 г., представленные в табл. 1 раздела 5.2. Данные
от 1 ноября до 27 ноября будут рассматриваться как выборочное множество на-
блюдений для предсказания значений ставок доходности на 28 ноября. Истин-
ное значение ставки доходности для срока погашения 0,25 года равно 5,53%.
Если мы используем марковскую модель только для данных срока погашения
0,25 года, мы получим оценку предсказания 5, 506 (см. пример раздела 5.2). Ес-
222
-0,08
-0,06
-0,04
-0,02
0
0,02
0,04
0,06
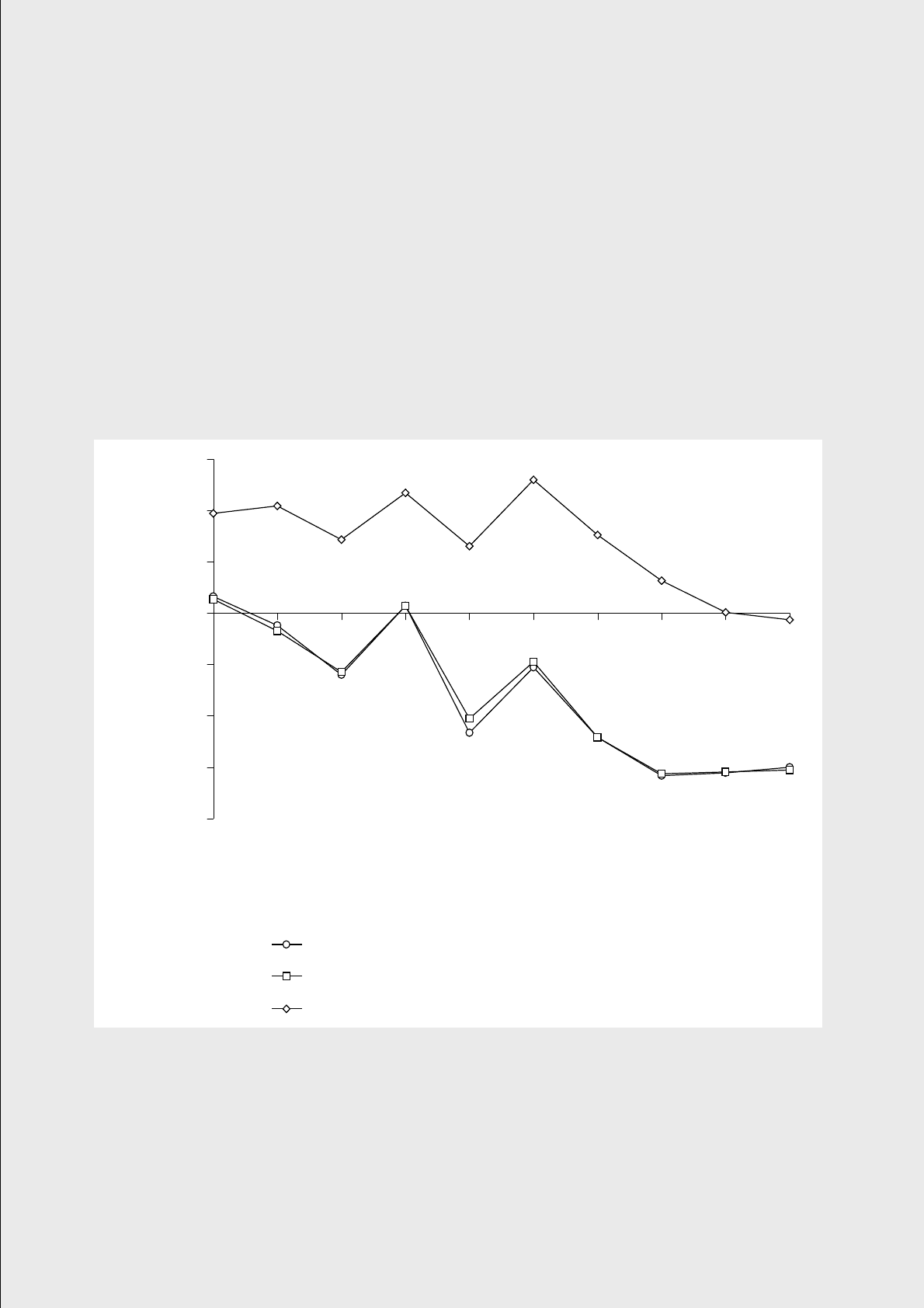
0,25 0,5 1 2 3 5 7 10 20 30
Срок погашения, годы
Ошибки (%)
ошибки предсказания для модели AR2
ошибки предсказания для модели AR1
ошибки тривиального предсказания
ли мы используем двумерную марковскую модель с данными только для сро-
ков погашения 0,25 и 0,5 лет, мы получим оценку предсказания 5, 507. Если же
мы привлечем данные всех десяти сроков погашения, т. е. используем десяти-
мерную марковскую модель, мы получим оценку предсказания 5,5301, или ис-
тинное значение ставки доходности на 28 ноября.
Второе выборочное множество образуется данными от 10 августа 1995 г.
по 3 января 1996 г. (100 значений доходности), и предсказываемой величиной
является доходность на 4 января 1996 г. (n = 1). Численные результаты предска-
зания представлены на рис. 1 в виде ошибок предсказания доходности для раз-
личных сроков до погашения и трех вариантов оценивания: тривиального пред-
сказания (оценка равна тренду процесса доходности), предсказания с помощью
модели AR(1) (марковский случай) и предсказания с помощью модели AR(2)
(только в случае т = р).
Рис. 1.
Для этого размера выборки точности предсказания с помощью скалярных и
матричных моделей принимают практически одинаковое значение (ср. с ре-
зультатами на рис. 1 в разделе 5.2). Интересно, что для больших значений сро-

223
ков погашения (10, 20 и 30 лет) тривиальное предсказание оказалось более точ-
ным.
ПРИМЕНЕНИЕ К ОПРЕДЕЛЕНИЮ ЦЕНЫ ОПЦИОНОВ
Инвестор, который хочет купить или продать опционы на фьючерсные
контракты на казначейские билеты или облигации хотел бы знать наиболее
точную цену опционов на фьючерсы за день (или несколько дней) до этого.
Обычно для определения цены опционов используется модель Блэка определе-
ния цены опционов на фьючерсы. Эта модель предполагает наличие пяти пара-
метров для вычисления цены опциона (см. раздел 1.1). Два из них, время исте-
чения и цена исполнения (strike price), могут считаться известными. Третий па-
раметр, цена фьючерсного контракта, может быть известен из данных преды-
дущего торгового дня. Оставшиеся два параметра, ставка доходности и ее вола-
тильность, являются наиболее неопределенными, поскольку они порождаются
случайным процессом ставки доходности. Этот случайный процесс рассматри-
вался выше, и предсказанные значения доходности, а также ее дисперсия могут
быть вычислены тем же самым путем, который был использован для построе-
ния доверительных интервалов. Используя эту информацию, инвестор, который
собирается совершить сделку, может вычислить цену опциона на фьючерс ут-
ром делового дня до начала торговли.
