Медведев Г.А. Математические модели финансовых рисков. Часть 1

124

(

)

(

)

(

)

() () ()

()

(

)

()

Uh Uh Uh

Un hUn h Un h

Ykh

n

12 13 1

2

3

22 2

11 1

...

... ... ... ...

...

-- -

æ

è

ç

ö

ø

÷

´

æ

è

ç

ö

ø

÷

=

(

)

()

(

)

(

)

()

()()

()

=

+-

+- - -

æ

è

ç

ö

ø

÷

-

Yk h UhYkh

Yk h U hYkh

Ykn h U n hYkh

1111

1

22

11

...

()

-

+-

+- -

æ

è

ç

ö

ø

÷

+

+-

ò

s

tt

Uk h dW

Ukn h dW

n

kh

n

kh

n

kh

kn h

1

2

1

2

1

...

()

Ykh

n

2

3

...

æ

è

ç

ö

ø

÷

=

() () ()

()

Uh Uh Uh

Un hUn h Un h

n

12 13 1

1

22 2

11 1

...

... ... ... ...

...

-- -

æ

è

ç

ö

ø

÷

-

процесса в последовательные дискретные моменты времени через временные

интервалы длительностью h . Представим это в математической форме. Запи-

шем первые п – 1 уравнений (19) в виде

(20)

.

Отсюда следует, что компоненты вектора Y , которые необходимо исключить,

определяются в виде

=

ç

´

125

(

)

()

(

)

(

)

()

()()

()

´

+-

+- - -

æ

è

ç

ö

ø

÷

-

Yk h UhYkh

Yk h U hYkh

Ykn h U n hYkh

1111

1

22

11

...

() () ()

()

-

-- -

æ

è

ç

ö

ø

÷

´

-

s

Uh Uh Uh

Un hUn h Un h

n

12 13 1

1

22 2

11 1

...

... ... ... ...

...

()

´

+-

+- -

æ

è

ç

ö

ø

÷

+

+-

ò

Uk h dW

Ukn h dW

n

kh

n

kh

n

kh

kn h

1

2

1

2

1

tt

...

() () ()

()

Uh Uh Uh

Un hUn h Un h

n

12 13 1

1

22 2

11 1

...

... ... ... ...

...-- -

æ

è

ç

ö

ø

÷

-

. (21)

То есть значения производных порядков от 1 до (n – 1) основного процесса в

момент времени kh выражаются через значения этого процесса в моменты

времени kh , (k + 1)h , ... , (k + n – 1)h и стохастические интегралы по соответ-

ствующим интервалам времени (kh,(k+1)h) , (kh,(k+2)h) , ... , (kh,(k+n–1)). Заме-

тим, что эти интервалы интегрирования последовательно вкладываются друг в

друга, поэтому компоненты последнего вектора в (21) являются зависимыми

случайными величинами. Введем для краткости вектор V

V = (V

2

V

3

... V

n

) = (U

12

(nh) U

13

(nh) ... U

1n

(nh)) ´

´

. (22)

Используя формулы (21) и (22), последнее уравнение (19) при m = n можно

написать в следующей форме:

y((n+k)h) = Y

1

((n+k)h) = U

11

(nh)Y

1

(kh) +

126

()

() ( )

()

()()

()

Yk h UhYkh

Yk h U hYkh

Yk n h U n hYkh

1111

1

22

11

+-

+- - -

æ

è

ç

ö

ø

÷

-

...

()

Uk h dW

Ukn h dW

n

kh

n

kh

n

kh

kn h

1

2

1

2

1

+-

+- -

æ

è

ç

ö

ø

÷

+

+-

ò

tt

...

()

(

)

()

Uknh dW

n

kh

knh

1

+-

+

ò

tt

()

(

)

()

Uknh dW

n

kh

knh

1

+-

+

ò

tt

()

´

+-

+- -

æ

è

ç

ö

ø

÷

+

+-

ò

Uk h dW

Ukn h dW

n

kh

n

kh

n

kh

kn h

1

2

1

2

1

tt

...

()

tUknh dW

n

kj h

kjh

j

n

1

+-

+

=

ò

å

+ (V

2

V

3

... V

n

) ´

– s (V

2

V

3

... V

n

) ´ +

+ s

. (23)

Полученное соотношение является рекуррентным выражением значения слу-

чайного процесса, который следует уравнению (2), в момент времени (k+n)h

через n предыдущих значений этого процесса в моменты времени kh , (k+1)h ,

... , (k+n–1)h и некоторые случайные компоненты в виде стохастических инте-

гралов, зависящие от реализации винеровского процесса на временном интер-

вале (kh,(k+n)h). Такое соотношение уже может рассматриваться как реализуе-

мая математическая модель процесса, так как она не содержит производных.

Стохастическая компонента этого соотношения может быть представлена в бо-

лее удобной для анализа форме следующим образом.

s

–

– s (V

2

V

3

... V

n

) =

=

st –

127

()

tVU k mh dW

mn

kj h

kjh

j

m

n

+

+-

+

==

-

+-

ò

åå

11

1

11

1

()

ttUknh dW

n

kj h

kjh

j

n

1

+-

+

=

ò

å

()

tVU k mh dW

mn

mj

n

kj h

kjh

j

n

+

=

-

+-

+

=

-

+-

é

ë

ê

ù

û

ú

å

ò

å

11

1

()

(

)

()

Uknh dW

n

kn h

knh

1

+-

+

ò

tt

()

ttUknh VUkmh dW

nmn

mj

n

kj h

kjh

j

n

111

1

+-- + -

é

ë

ê

ù

û

ú

+

=

-

+-

+

=

-

å

ò

å

()

U n jh s V U m jh s dW k jh s

nmn

mj

n

h

111

1

0

-+- -+

é

ë

ê

ù

û

ú

+-

+

=

-

å

ò

()

(

)

()

Uknh dW

n

kh

knh

1

+-

+

ò

tt

()

´

+-

+- -

æ

è

ç

ö

ø

÷

+

+-

ò

Uk h dW

Ukn h dW

n

kh

n

kh

n

kh

kn h

1

2

1

2

1

tt

...

()

Zkn

j

n

,

=1

–st =

=

s – (24)

–

st =

= s

+

st .

Обозначим для j = 1, 2, ... , n

Z

j

(k,n) = s (25)

(в случае j = n сумма в квадратных скобках под интегралом равна нулю; пере-

менная интегрирования s = (k + j)h – t ). Тогда стохастическая компонента со-

отношения (23) представляется в виде суммы

s

–

– s (V

2

V

3

... V

n

) =

å

. (26)

Преимущество такого представления состоит в том, что из структуры выраже-

ния (25) следует, что слагаемые суммы (26) являются независимыми в совокуп-

ности нормально распределенными случайными величинами с нулевыми мате-

матическими ожиданиями и дисперсиями, определяемыми следующими выра-

жениями:

128

()

[]

2

1

2

0

Usds

n

h

ò

()

2

111

1

0

2

Unjhs VUmjhsds

nmn

mj

n

h

-+- -+

é

ë

ê

ù

û

ú

+

=

-

å

ò

ay

mknm

m

n

+-

=

å

1

()

Zkn

j

n

,

=

å

1

()

VU jh

j

n

+

=

-

111

1

ay

mknm

m

n

+-

=

1

b

jknj

j

n

x

+-

=

-

0

1

Var[Z

n

(k,n)] = s ; (27)

Var[Z

j

(k,n)] = s . (28)

Для краткости в дальнейшем будем обозначать y

k

= y(kh) º Y

1

(kh). Таким обра-

зом, соотношение (23) приобретает простой вид:

y

k+n

= + , (29)

где коэффициенты a

m

, согласно уравнению (23), вычисляются по формулам:

a

n

= U

11

(nh) –

å

, a

m

= V

n+1–m

, m = 1, 2, ... , n – 1. (30)

Отсюда следует, что решение стохастического уравнения (2), наблюдаемое в

дискретные моменты времени через равные интервалы, похоже на формулу ав-

торегрессии - скользящего среднего порядка (n,n) (ARMA(n,n)). Более при-

вычной формой ARMA(n,n) является выражение

y

k+n

=

å

+

å

, (31)

где x

k+1

, ... , x

k + n

независимые в совокупности случайные величины с нуле-

вым математическим ожиданием и единичной дисперсией, а коэффициенты

скользящего среднего b

j

=(Var[Z

n–j

(k,n)])

1/2

определяются с помощью формул

(27) и (28). Однако в нашем случае нет полной эквивалентности между Z

n–j

(k,n)

и b

j

x

k + n – j

, так как их корреляционные свойства различаются. В частности, для

0 £ l £ n – 1 , 0 £ j £ n – l – 1

Cov(b

j

x

k + n – j

, b

j + l

x

k + l + n – ( j + l)

) = b

j

b

j + l

=

= (Var[Z

n–j

(k,n)] ´ Var[Z

n – j – l

(k + l,n)])

1/2

. (32)

В то же самое время для этих же 0 £ l £ n – 1 , 0 £ j £ n – l – 1

Cov(Z

n–j

(k,n) , Z

n – j – l

(k + l,n)) =

129

() ( )

()

2

111

1

0

Ujhs VU mnjhs

nmn

mn j

n

h

+- -+ +

é

ë

ê

ù

û

ú

+

=-

-

å

ò

()

´++- -+++

é

ë

ê

ù

û

ú

+

=--

-

å

Ujlhs VUmnjlhsds

nmn

mn jl

n

111

1

l

21

2

,

=- ± -aab

B =

æ

è

ç

ö

ø

÷

11

12

ll

B

-

=

-

æ

è

ç

ö

ø

÷

1

21

2

1

ll

l

1

21

ll-

11

12

ll

æ

è

ç

ö

ø

÷

e

t

l

1

2

0

æ

è

ç

ö

ø

÷

l

2

1

-

æ

è

ç

ö

ø

÷

= s ´ (33)

.

Сравнение выражений (32) и (33) дает, что по неравенству Коши - Буняковско-

го

|Cov(Z

n–j

(k,n) , Z

n – j – l

(k + l,n))| £ |Cov(b

j

x

k + n – j

, b

j + s

x

k + l + n – ( j + l)

)| ,

Поскольку корреляционные свойства процесса скользящего среднего сущест-

венно влияют на дисперсию процесса y(t) , то использование обычной модели

ARMA(n,n), определяемой формулой (31), является проблематичным, и следует

в качестве разностной версии стохастического дифференциального уравнения

(2), рассматриваемой как реализуемая математическая модель, использовать

соотношение (29) с учетом соотношений (25) и (30).

УРАВНЕНИЕ ВТОРОГО ПОРЯДКА

При условии n = 2 имеем наиболее простой случай. Пусть уравнение (2)

имеет вид

dу

(1)

(t) + 2а у

(1)

(t) dt + bу(t) dt = s dW(t) . (34)

Корни характеристического полинома находятся из уравнения

l

2

+ 2al + b = 0 , . (35)

Матрицы В и В

– 1

(см. (17) и (18)) имеют вид

, . (36)

Фундаментальная матрица решений U(t)

U(t) =

=

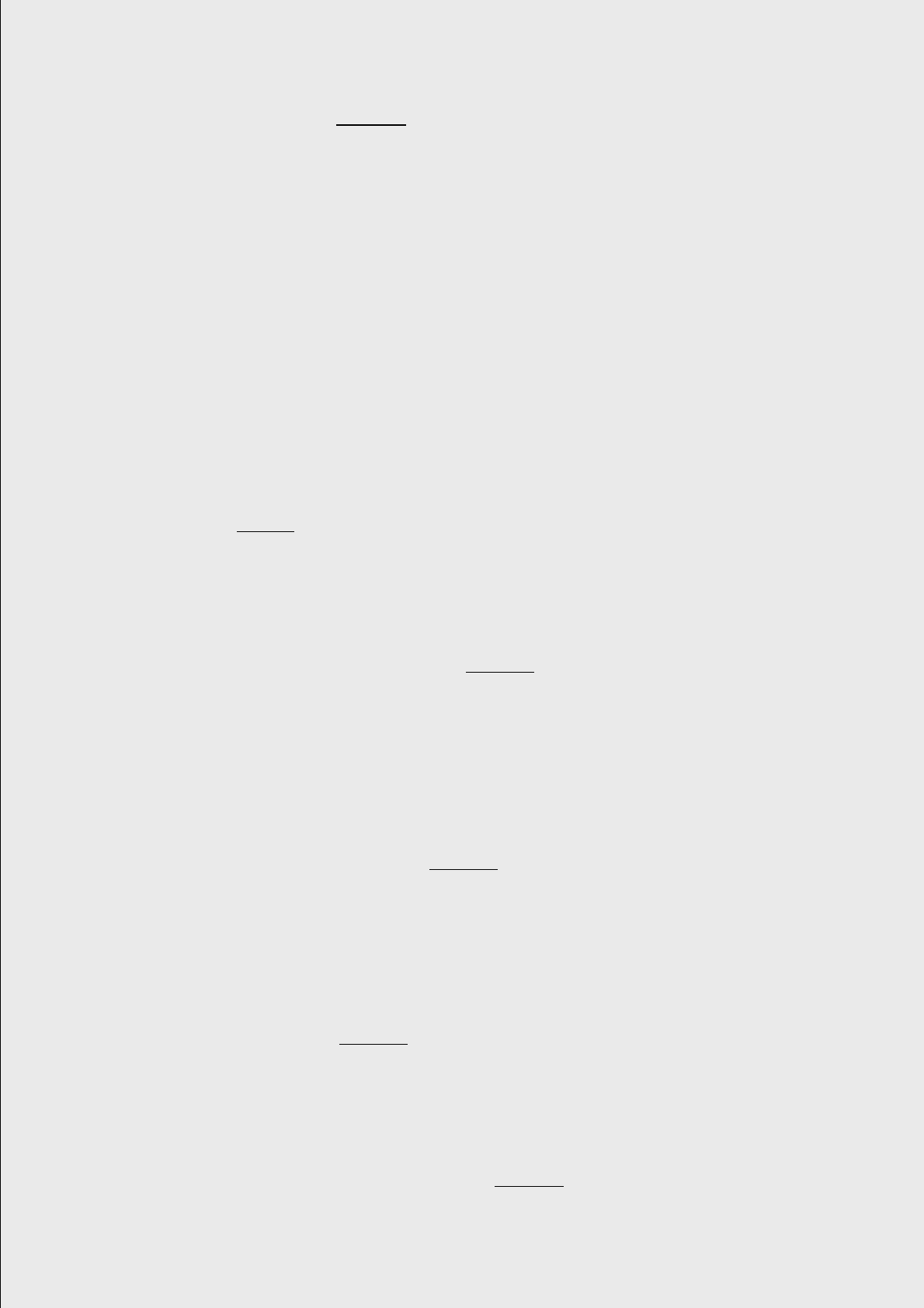
130

()

1

21

2

1

212

21

12

2

1

ll

ll l l

ll ll

ll l l

-

--+

--

æ

è

ç

ö

ø

÷

ee ee

ee e e

tt tt

tt t t

()()

tUh dW kh

h

12

0

2

2 -+

ò

()( )

tUh dW kh

h

12

0

-+

ò

()

1

12

Uh

()( )

tUh dW kh

h

12

0

-+

ò

(

)

()

Uh

12

2

()( )

tUh dW kh

h

12

0

-+

ò

()()

tUh dW kh

h

12

0

2

2 -+

ò

()()

sttUh dW kh

h

12

0

2

2 -+

ò

(

)

()

Uh

12

2

()( )

sttUh dW kh

h

12

0

-+

ò

() ()

()

tUh dW k h

h

12

0

1-++

ò

()

(

)

()

()( )

ttUh

Uh

Uh dW kh

h

12

0

2

-- -

é

ë

ê

ù

û

ú

+

ò

()

(

)

()

()( )

ttUh

Uh

Uh dW kh

h

12

0

2

-- -

é

ë

ê

ù

û

ú

+

ò

= . (37)

Уравнения (19) принимают вид

y((k+2)h) = U

11

(2h)y(kh) + U

12

(2h)y'(kh) + st ;

y((k+1)h) = U

11

(h)y(kh) + U

12

(h)y'(kh) + st . (38)

Система (20) вырождается в единственное уравнение для определения произ-

водной y

(1)

(kh) из второго уравнения (38). Поэтому в этом случае нет необхо-

димости использовать представление (22) и выражение (21) выписывается в яв-

ной форме:

y

(1)

(kh) = ( y((k+1)h) – U

11

(h)y(kh) – st ). (39)

Решение в форме (23) дается выражением

y((k+2)h) = U

11

(2h)y(kh) + [ y((k+1)h) – U

11

(h)y(kh) –

–

st ] + st . (40)

Стохастическая компонента выражения (40) имеет вид

– =

=

st +

+

st . (41)

Так что

Z

1

(k,2) = st ; (42)

131

() ()

()

tUh dW k h

h

12

0

1-++

ò

()

tt

2

12

2

0

2

Uh

Uh d

h

-- -

é

ë

ê

ù

û

ú

ò

()

[]

tt

2

12

2

0

Uh d

h

-

ò

()

(

)

()

()()

ttt

2

12

12 12

0

2

Uh

Uh Uh d

h

-- -

é

ë

ê

ù

û

ú

-

ò

()

1

21

2

1

2

ll

-

-ee

tt

()

1

21

ll

-

-ee

tt

(

)

()

Uh

ee

hh

12

21

2

=+

ll

()

(

)

()

Uh

Uh e

h

11

12

11

12

2

-=-

+ll

Z

2

(k,2) = st . (43)

Случайные величины Z

1

(k,2) и Z

2

(k,2) являются независимыми и имеют нуле-

вые математические ожидания и дисперсии, вычисляемые по формулам:

Var[Z

1

(k,2)] = st ; (44)

Var[Z

2

(k,2)] = s . (45)

Корреляционные свойства этих случайных величин определяются соотношени-

ем (для других различающихся значений параметров ковариация равна нулю)

Cov[Z

2

(k,2), Z

1

(k+1,2)] =

=

st . (46)

Из выражения (37) следует, что необходимые элементы фундаментальной мат-

рицы решений U(t) имеют вид

U

11

(t) = ; (47)

U

12

(t) = . (48)

Поэтому

; (49)

; (50)

132

()

(

)

()

.

1

2

12

212121

t

ll

tt

lltltlll

--=-

-

=

=---

+--+

Ueeee

hU

hh

ee

hhll

21

+

(

)

-

+

e

hll

12

()

[]

t

ll

2

12

2

0

eUd

h

+

-

ò

()

()( )

()()

s

ll l l

ll l l l l

ll

ll l l

2

12

12 1 2

12

21

2

1

2

12 2 1

2

12

2

e

ee e e

h

hh h h

+

-

-+ -

-+

é

ë

ê

ù

û

ú

()

[]

tt

2

12

2

0

Ud

h

ò

(

)

(

)

()()

()

s

ll l l

ll l l l l

ll l l

2

12

2

12

2

12 2 1

2

12

12 1 2

2

1

21 2 1

ee e e

hh h h

-+ -

-+

-

+

é

ë

ê

ù

û

ú

()

()()

---

+

ò

sttt

ll

2

12 12

0

12

eUhUd

h

()

s

ll

ll l l2

2

1

2

12

2

12

11 2 2

eeeee

h

hh h h

+

--

-

+

-

é

ë

ê

ù

û

ú

(51)

Таким образом, соотношение (40), задающее разностную модель стохастиче-

ского процесса, определяемого стохастическим дифференциальным уравнени-

ем (34), имеет вид

y

k+2

= a

1

y

k+1

+ a

2

y

k

+ Z

1

(k,2) + Z

2

(k,2) , (52)

где коэффициенты a

1

и a

2

определяются по формулам

a

1

= , a

2

= , (53)

а случайные величины Z

1

(k,2) и Z

2

(k,2) имеют следующие вероятностные ха-

рактеристики:

g = Var[Z

1

(k,2)] = st =

=

; (54)

d = Var[Z

2

(k,2)] = s =

=

; (55)

e = Cov[Z

2

(k,2), Z

1

(k+1,2)] = =

=

. (56)

133

()

()()

[]

1

22

21

2

1

12

0

ee

eeZkjZkj

jj

j

-

--+-

++

=

¥

å

,,

ee

h

1

=

l

ee

h

2

=

l

Ce Ce

kk

11 2 2

+ Ce

hk hk

12

ll

+

()

C

ee

ee e ee

1

11

2

12 1

2

12

1

11

=

+++

---

gd e

()

C

ee

ee e ee

2

22

2

21 2

2

12

1

11

=

+++

-- -

gd e

Заметим, что процесс, определяемый уравнением (34), будет устойчивым (кау-

зальным - causal), если собственные числа l

1

и l

2

отрицательные (или имеют

отрицательную вещественную составляющую, когда они являются комплексно

сопряженными). Иначе говоря, если в уравнении (34) a > 0 . Пользуясь техни-

кой исследования временных рядов, в этом случае можно представить времен-

ной ряд (52) в виде

y

k+2

= , (57)

где для краткости обозначено

, . (58)

Тогда соотношения (52) и (57) позволяют получить уравнения Юла - Уокера

для корреляционной функции r(t) временного ряда (52):

r(0) – (e

1

+ e

2

)r(1) + e

1

e

2

r(2) = g + d + (e

1

+ e

2

) e ; (59)

r(1) – (e

1

+ e

2

)r(0) + e

1

e

2

r(1) = e ; (60)

r(k + 2) – (e

1

+ e

2

)r(k + 1) + e

1

e

2

r(k) = 0 , k ³ 0 . (61)

Уравнению (61) удовлетворяет функция

r(k) =

º Ce . (62)

Подстановка функции (62) в уравнения (59) и (60) приводит к системе уравне-

ний относительно коэффициентов C

1

и C

2

, которые определяются формулами

(63)

.

Формулы (58), (62) и (63) полностью определяют корреляционную функцию

процесса y

k

, задаваемого соотношением (52). Заметим, что дисперсия этого

процесса равна r(0) = C

1

+ C

2

, что позволяет найти ее в виде

Медведев Г.А. Математические модели финансовых рисков. Часть 1

Подождите немного. Документ загружается.