Майсеня Л.И. Математика в примерах и задачах. Часть 2

83 84

Пример 2. Выполнить действия:

1)

1

16cossincossin;

33866

ii

pppp

æöæö

+×+

ç÷ç÷

èøèø

2)

( )

55

2232cossin;

1212

ii

pp

æö

-×+

ç÷

èø

3)

77155

cossin:cossin.

66266

ii

pppp

æö

æöæöæö

--+-

ç÷

ç÷ç÷ç÷

èøèøèø

èø

Решение. 1) Используя формулу (7.35), находим:

1

16cossin2cossin2.

8363622

iii

pppppp

æö

æöæöæö

×+++=+=

ç÷ç÷ç÷ç÷

èøèøèø

èø

2) Сначала представим число

22

i

-

в тригонометрической форме.

Имеем

22.

z = Поскольку число лежит в IV четверти и

tg1,

j

=-

то

.

4

p

j

=-

Следовательно,

2222cossin.

44

ii

pp

æö

æöæö

-=-+-

ç÷

ç÷ç÷

èøèø

èø

Теперь воспользуемся формулой (7.35):

55

22cossin32cossin

441212

ii

pppp

æö

æöæöæö

-+-×+=

ç÷

ç÷ç÷ç÷

èøèøèø

èø

55

2232cossin

412412

31

12cossin1212636.

6622

i

iii

pppp

pp

æö

æöæö

=×-++-+=

ç÷

ç÷ç÷

èøèø

èø

æö

=+=+×=+

ç÷

èø

Получаем ответ:

636.

i

+

3) Заметим, что делимое число не записано в тригонометрической

форме. Запишем его в этой форме. Получим:

7777

cossincossin.

6666

ii

pppp

æöæöæö

-=-+-

ç÷ç÷ç÷

èøèøèø

Используя формулу (7.36), находим:

77155

cossin:cossin

66266

ii

pppp

æöæö

æöæöæöæö

-+--+-=

ç÷ç÷

ç÷ç÷ç÷ç÷

èøèøèøèø

èøèø

17575

1:cossin

26666

i

pppp

æö

æöæöæö

=-++-+=

ç÷

ç÷ç÷ç÷

èøèøèø

èø

22

2cossin.

33

i

pp

æö

æöæö

=-+-

ç÷

ç÷ç÷

èøèø

èø

Переходя к алгебраической форме, получаем в ответе

13.

i

-

Пример 3. Возвести в степень выражение

(

)

9

13.

i

-+

Решение. Представим число

13

i

-+ в тригонометрической фор-

ме. Здесь

2,

r

=

tg3

j

=-

и соответствующая точка лежит во II чет-

верти, т. е.

2

.

3

p

j

= Получили

22

132cossin.

33

zii

pp

æö

=+=+

ç÷

èø

По

формуле (7.37) находим:

( )

99

22

2cos9sin9512cos6sin6512.

33

zii

pp

æö

æöæö

=×+×=+=

ç÷ç÷ç÷

èøèø

èø

Получаем ответ: 512.

Пример 4. Извлечь корень. Полученные значения корня изобра-

зить на комплексной плоскости:

1)

13

;

22

i

-+ 2)

3

8.

i

Решение. 1) Находим модуль и аргумент числа

13

.

22

i

-+

Получаем

2

1,.

3

z

p

j

== Далее, используя формулу (7.38), вы-

числяем:

22

13

33

cossin,

2222

k

kk

wii

pp

++

æö

ç÷

=-+=+

ç÷

èø

где

0,1.

k =

Если

0,

k

=

то

0

13

cossin;

3322

wii

pp

=+=+

если

1,

k

=

то

1

4413

cossin

3322

wii

pp

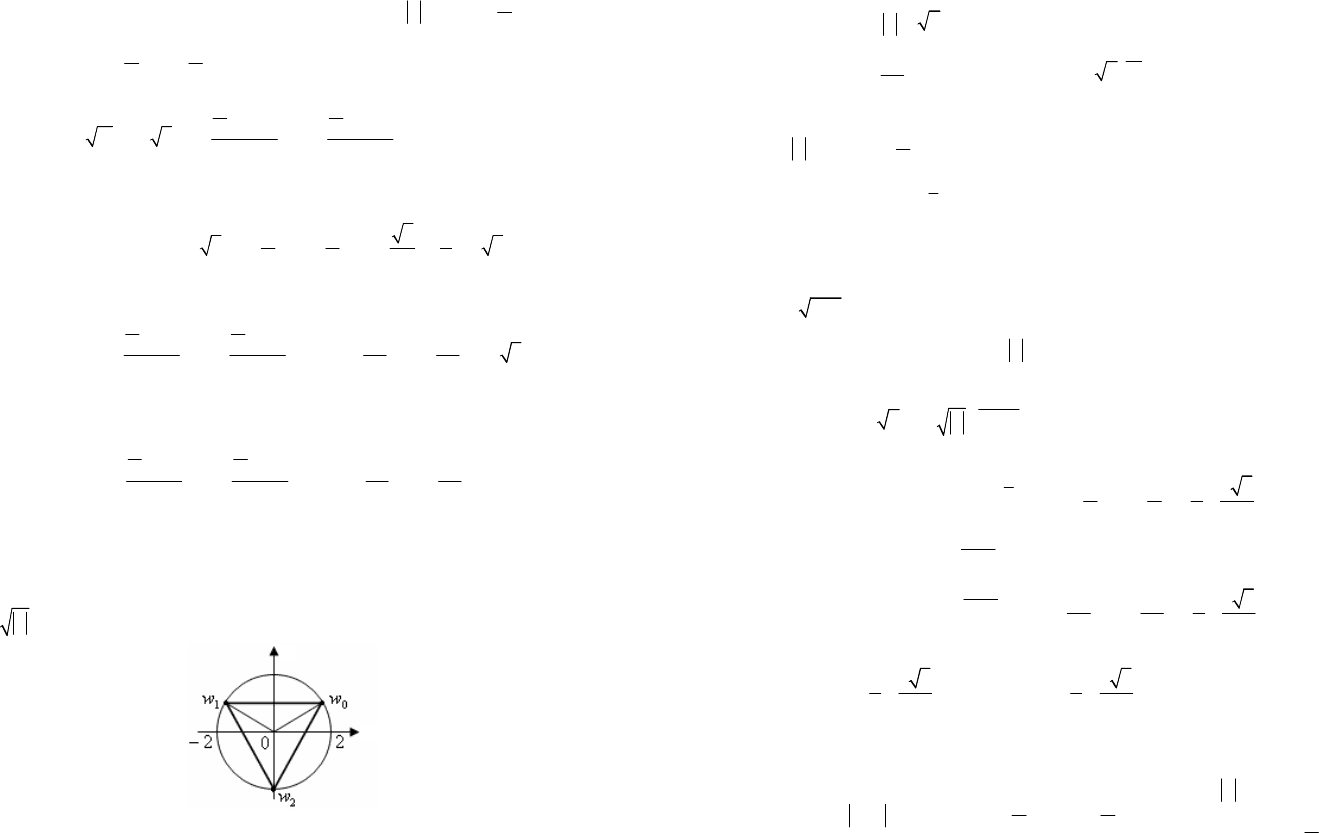
=+=-- (рис. 7.32).

Рис. 7.32

у

х

85 86

2) Находим модуль и аргумент числа

8:

zi

=

8,

z

=

.

2

p

j

= Полу-

чили

88cossin.

22

ii

pp

æö

=+

ç÷

èø

Тогда, используя формулу (7.38), имеем:

( )

33

22

88cossin,

33

k

kk

wii

pp

æö

++

ç÷

==+

ç÷

èø

где

0,1,2.

k =

Если

0,

k

=

то

3

0

31

8cossin23;

6622

wiii

pp

æö

=+=+=+

ç÷

èø

если

1,

k

=

то

1

22

55

22

2cossin2cossin3;

3366

wiii

pp

æö

++

ç÷

æö

=+=+=-+

ç÷

èø

ç÷

èø

если

2,

k

=

то

2

44

33

22

2cossin2cossin2.

3322

wiii

pp

æö

++

ç÷

æö

=+=+=-

ç÷

èø

ç÷

èø

Изобразим комплексные числа

012

,,.

www

На комплексной плос-

кости точки, соответствующие значениям корня, являются вершинами

правильного треугольника, вписанного в окружность радиусом

3

2

z

=

с центром в начале координат (рис. 7.33).

Рис. 7.33

Пример 5. Представить число в показательной форме:

1)

1;

i

-+

2)

6.

i

-

Решение. 1) Находим модуль и аргумент комплексного числа

1:

zi

=-+

2,

z =

tg1

j

=-

и число лежит во II четверти, следова-

тельно

3

.

4

p

j

=

Получили

3

4

12.

i

zie

p

=-+=

2) Находим модуль и аргумент комплексного числа

6:

zi

=-

6,

z

=

.

2

p

j

=-

Тогда, по формуле (7.40) имеем:

2

66.

i

zie

p

-

=-=

Пример 6. Решить уравнение

3

270.

z

+=

Решение.

3

27.

z

=-

Искомыми корнями уравнения будут значения

(

)

3

27, 0, 1, 2.

k

k-=

Для 27

-

=

z имеем

27,

z =

arg.

z

jp

==

Тогда

27.

i

ze

p

= По

формуле (7.44) получаем:

( )

2

3

,

k

i

k

wzze

pp

+

==

где k = 0, 1, 2.

Если k = 0, то

3

0

333

33cossin;

3322

i

weii

p

pp

æö

==+=+

ç÷

èø

если k = 1, то

( )

2

3

1

33cossin3;

i

wei

pp

+

==+=-

если k = 2, то

4

3

2

55333

33cossin.

3322

i

weii

pp

+

æö

==+=-

ç÷

èø

Таким образом, корнями заданного уравнения являются числа:

0

333

;

22

wi

=+

1

3;

w

=-

2

333

.

22

wi

=-

Пример 7. Изобразить на комплексной плоскости множество то-

чек, для которых:

1)

12;

z

+=

2)

arg;

63

z

pp

<£ 3)

1,

0arg.

4

z

p

ì

>

ï

í

££

ï

î

Решение. 1) Пусть

,

zxyi

=+

тогда

(

)

111.

zxyixyi

+=++=++

у

х

87 88

Найдем модуль полученного комплексного числа

( )

2

11.

zxy

+=++

Тогда заданное равенство будет иметь вид:

( )

2

12

xy

++=

или

( )

2

22

12.

xy++=

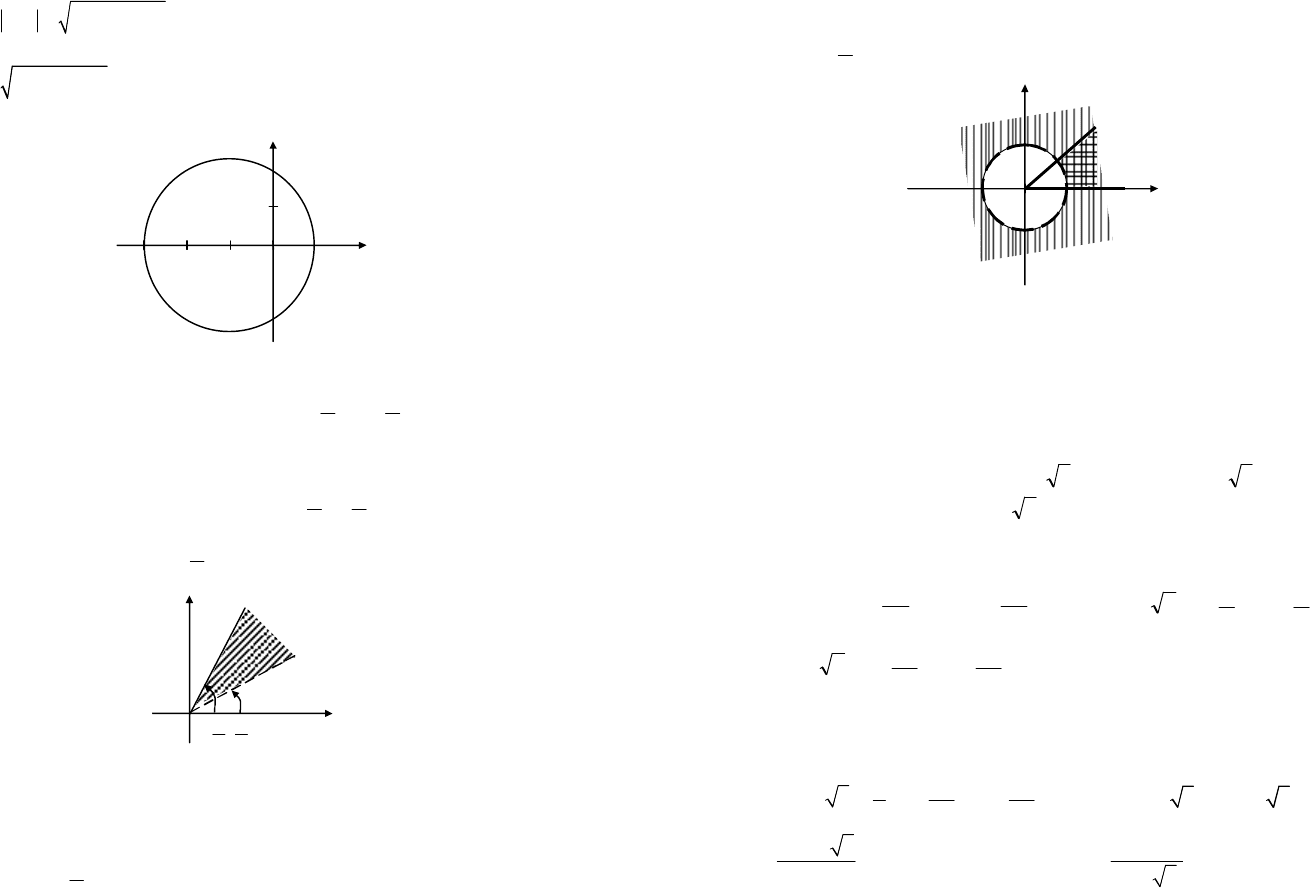
Это уравнение окружности радиуса 2 с центром в точке

(

)

1; 0

C -

(рис. 7.34).

Рис. 7.34

2) Пусть

arg.

z

j

=

Из условия имеем

.

63

pp

j

<£ Геометрически

это неравенство задает на плоскости множество точек, лежащих внут-

ри угла с вершиной в точке (0; 0), стороны которого составляют с по-

ложительным направлением оси Ох углы

6

p

и

,

3

p

а также множество

точек, лежащих на луче

3

p

j

=

(рис. 7.35).

Рис. 7.35

3) Заданная система равносильна следующей:

22

1,

0.

4

xy

p

j

ì

+>

ï

í

££

ï

î

Решением системы будет пересечение множества точек, лежащих

вне окружности

22

1,

xy

+=

и множества точек, лежащих внутри угла

величины

4

p

и на его сторонах (рис. 7.36).

Рис. 7.36

Задания

I уровень

1.1. Представьте число в тригонометрической и показатель-

ной формах, изобразите его на плоскости:

1) ;iz 2

-

=

2) ;iz 388 -= 3) ;,, iz 51351 +=

4) ;12

=

z 5)

(

)

;iz 25 -= 6) .iz 1010

+

-

=

1.2. Представьте комплексное число в алгебраической форме:

1)

;sincos

÷

ø

ö

ç

è

æ

÷

ø

ö

ç

è

æ

-+

÷

ø

ö

ç

è

æ

-=

3

2

3

2

pp

iz

2) ;sincos

÷

ø

ö

ç

è

æ

+=

44

25

pp

iz

3)

.sincos

÷

ø

ö

ç

è

æ

+-=

4

3

4

3

2

pp

iiz

1.3. Используя тригонометрическую формулу комплексного

числа, выполните действия:

1)

( )

155

33cossin;

266

ii

pp

æö

-+×+

ç÷

èø

2)

(

)

(

)

443223;

ii

-+×+

3)

223

;

1

i

-+

-

4)

8

;

223

i

+

–

3

–

1

х

0

y

С

6

p

3

p

х

0

y

–

1

х

0

y

89 90

5)

2226

;

3344

i

æö

-×-+

ç÷

èø

6)

3cossin

33

;

3

i

pp

æö

+

ç÷

èø

-

7)

23252222

3cossin23cossin.

45454545

ii

pppp

æöæö

+×+

ç÷ç÷

èøèø

1.4. Возведите в степень:

1)

;sincos

9

1818

÷

ø

ö

ç

è

æ

+

pp

i

2)

;sincos

8

1812

2

÷

ø

ö

ç

è

æ

÷

ø

ö

ç

è

æ

+×

pp

i

3)

(

)

;

5

22 i+ 4) .

10

3

÷

ø

ö

ç

è

æ

-- i

1.5. Представив комплексные числа ,iz --= 1

1

,iz 22

2

-=

iz 31

3

+= в тригонометрической форме, вычислите .

2

31

4

z

zz

×

1.6. Вычислите корни из комплексных чисел и дайте геомет-

рическую интерпретацию их значений:

1) ;i

2

1

2

3

- 2)

;

3

27i

3)

;i--1

4) ;i366 +-

5)

;

3

125-

6) ;

3

8

i-

7)

;i44 -

8)

.

3

i-

1.7. Выполните действия, результат запишите в алгебраиче-

ской форме:

1)

(

)

;

100

3 i- 2)

( )

(

)

;

i

2

1

12

4

+

3) ;

sincos

÷

ø

ö

ç

è

æ

+

÷

ø

ö

ç

è

æ

+

66

2

33

3

pp

i

4)

3

1111

2cossin

99

;

122

cossin

499

i

pp

æö

+

ç÷

èø

ç÷

æö

ç÷

+

ç÷

èø

5)

(

)

;

i

-

1

22

6

6)

(

)

3

.

13

i

+

1.8. Решите уравнение:

1)

2

340;

zz

-+=

2) ;01

3

=-z

3) ;082

2

=+z 4) ;01

2

=++ zz

5)

2

143

230.

22

i

zzi

-

æö

++-=

ç÷

èø

1.9. Изобразите на комплексной плоскости множество точек,

для которых:

1) ;133 £+- iz 2) ;21 >+z 3)

2Im5;

z

-£<

4) ;2121 £-< z 5) ;ImRe 1

£

+

zz 6) ;arg

3

6

pp

£<- z

7) ;1642 ³-+ iz 8)

ï

î

ï

í

ì

<£-

³

.arg

,Re

44

1

pp

z

II уровень

2.1. Представьте число в тригонометрической и показатель-

ной формах:

1) ;

i

z

+

-

=

1

2

2) ;sincos

6

pp

iz -=

3) ;,, iz 50350 --= 4)

(

)

(

)

;iiz -×+= 121

5)

;cossin

÷

ø

ö

ç

è

æ

+=

3

2

3

2

6

pp

iz

6) .31 -=z

2.2. Даны комплексные числа iz 322

1

+-= и

.iz -=1

2

Представив их в тригонометрической форме, вычислите:

1) ;

21

5 zz × 2) ;

1

2

2z

z

3) ;

2

3

1

z

- 4)

.

6

2

z

91 92

2.3. Используя тригонометрическую форму комплексного

числа, выполните действия:

1)

(

)

( )

;

2

3

15252 ii +×+- 2)

( )

(

)

;,,

3

2

32502501 ii --

3)

;

sincos

2

60

17

60

17

30

7

30

7

4

÷

ø

ö

ç

è

æ

+

÷

ø

ö

ç

è

æ

+

pp

i

4)

( )

.

ii

i

621

434

++-

-

2.4. Возведите в степень, результат запишите в алгебраиче-

ской форме:

1) ;

20

1

÷

ø

ö

ç

è

æ

--

+

i

2) ;sincos

÷

ø

ö

ç

è

æ

+×

÷

ø

ö

ç

è

æ

-

+

44

2

1

100

pp

i

3)

( )

;

12

3

1

i-

4) .

40

1

31

÷

ø

ö

ç

è

æ

-

+

i

2.5. Вычислите корни, а результат изобразите на комплекс-

ной плоскости:

1) ;

4

16i 2) ;

4

4- 3) ;

5

1 i+-

4) ;

6

322 i- 5) ;

4

388 i-- 6) .

6

64i-

2.6. Решите уравнение:

1) ;064

2

=- iz 2) ;04

4

=+z

3) ;0432

24

=+- zz 4)

(

)

;05264

2

=-++ iizz

5) ;0164

24

=+- zz 6)

(

)

(

)

2

83131;

zizi

-+++

7)

( )

2

120.

i

ziz

+++=

2.7. Изобразите на комплексной плоскости множество точек,

для которых:

1)

( )

;arg

4

1

6

pp

£+< z 2) ;211 £-+£ iz

3)

(

)

î

í

ì

->

£+<

;Re

,Im

5

120

z

iz

4)

( )

ï

î

ï

í

ì

³+

£+-£

;Im

,arg

1

4

3

210

iz

p

5) ;21 >-++ izz 6)

ï

î

ï

í

ì

=--

=

.

,arg

21

4

iz

z

p

III уровень

3.1. Представьте в алгебраической и тригонометрической

формах комплексные числа и выполните действия:

1)

(

)

( )

;

,,

3

35051

650250

2

3

×

×+-

+

ii

i

2)

;

sincos

3

12

13

12

13

12

5

12

5

2

÷

ø

ö

ç

è

æ

-

+-

×

pp

i

3)

( )

;

cossin

i

ii

-

+-

÷

ø

ö

ç

è

æ

+

4

31

66

16

pp

4)

( )

.

cossin

2

132

44

24

ii

i

-×-

÷

ø

ö

ç

è

æ

÷

ø

ö

ç

è

æ

-+

÷

ø

ö

ç

è

æ

-

pp

3.2. Пусть ,iz 43

1

+= .iz 34

2

+-= Найдите действительные

значения a и b, для которых .

21

2

1

bzaz

z

+=

3.3. Изобразите множество точек комплексной плоскости,

координаты х и у которых удовлетворяют условию

.i

y

yyixix

12

14

122

2

-

+-=+-+

3.4. Найдите комплексное число z, удовлетворяющее урав-

нению

(

)

(

)

(

)

(

)

.iiizizi 7143121 +=-×-++×-

3.5. Определите, при каких действительных значениях х и у

комплексные числа

52

1

1049 xiyz --= и

112

2

208 iyz += явля-

ются сопряженными.

93 94

3.6. Решите уравнение:

1) ;0

1

22

3

=

-

i

z 2) ;2

5

=+- iz 3)

2

0;

zz

+=

4)

(

)

(

)

22

1212.

zzzz++×++=

3.7. Изобразите на комплексной плоскости множество точек,

удовлетворяющих следующим условиям:

1) ;iziz 42 +³+- 2)

Re182;

iz

++>

3) ;2³

-

+

iz

4)

( )

122,

0arg1.

2

zi

p

ì-<+£

ï

í

<+-£

ï

î

3.8. Найдите z

6

, если .izz 843

+

-

=

-

3.9. Найдите

a

и

b

, если известно, что комплексное число

i

b

a

+

является корнем уравнения .033

2

=++- ixx

3.10. Комплексное число z удовлетворяет условию .3

1

=+

z

Найдите z

18

.

94 95

8. ВЕКТОРЫ НА ПЛОСКОСТИ

8.1. Векторы и простейшие действия над ними

Под вектором на плоскости понимают направленный отре-

зок с началом в точке А и концом в точке B, который обознача-

ется

ÀÂ

(или

ÀÂ

uuur

). Модулем, или длиной,

AB

такого вектора

называется длина отрезка

.

AB

Если нет необходимости указывать начало и конец вектора,

то его обозначают

,,,...

abc или

,,,...

abc

Различают векторы связанные (закрепленные) с фиксиро-

ванным началом и свободные. Под свободным вектором

a

по-

нимают класс эквивалентных направленных отрезков, т. е. таких

отрезков, которые совмещаются при параллельном переносе.

Векторы a и b называются коллинеарными (обозначение:

||

ab

), если они лежат на одной прямой или на параллельных

прямых. Кроме того, если они имеют одинаковое направление,

их называют сонаправленными (обозначение:

ab

--

), а если

противоположное – противоположно направленными (обозна-

чение:

ab

-¯

).

Два вектора СDAB и называются равными, если они име-

ют одинаковые длины и являются сонаправленными. Записыва-

ется это с помощью обычного знака равенства:

.

ABCD

=

При этом запись ABa = понимают также в смысле, что начало

свободного вектора a приложено к точке А.

Вектор нулевой длины называется нулевым и обозначается

0.

Направление такого вектора считается неопределенным.

У нулевого вектора начальная и конечная точки совпадают.

Пусть заданы два ненулевых вектора

, .

ab

Отложим их от

некоторой точки О таким образом, чтобы

, .

OAaOBb

==

Под углом

(,)

ab

j

Ù

= между векторами

a

и

b

понимают наи-

меньший положительный угол, на который надо повернуть один

из векторов, чтобы его направление совпало с направлением

второго вектора. Этот угол не зависит от выбора точки О и из-

меняется от 0 до

p

.

Для векторов определены следующие линейные операции:

умножение вектора на действительное число и сложение векто-

ров

,.

ab

Произведением вектора

a

на действительное число λ на-

зывается вектор

,

a

l

×

удовлетворяющий следующим условиям:

1)

;

aa

ll

×=×

2)

, åñëè 0,

aa

ll

×-->

, åñëè 0,

aa

ll

×-¯<

0, åñëè 0 èëè 0.

aa

ll

×===

Для того чтобы сложить векторы

a

и

b

геометрически, ис-

пользуют правило треугольника: начало вектора

b

совмещает-

ся с концом вектора

,

a

их суммой является вектор

,

c

начало

которого совпадает с началом вектора

,

a

а конец – с концом

вектора

b

(рис. 8.1). Для обозначения этого действия использу-

ется обычный знак суммы:

.

cab

=+

Рис. 8.1

Сложение двух векторов можно производить также по пра-

вилу параллелограмма: векторы

a

и

b

приводятся к общему

началу, некоторой точке О, и на них строится параллелограмм.

Тогда суммой этих векторов является вектор

,

c

который совпа-

дает с диагональю построенного параллелограмма, исходящей

из точки О (рис. 8.2).

bac +=

b

а

96 97

Рис. 8.2

Сумма трех и более векторов

12

,,...,

n

aaa

может быть най-

дена по правилу замыкания (ломаной). Это вектор, начало ко-

торого совпадает с началом вектора

1

,

a

а конец – с концом век-

тора

n

a

(рис. 8.3).

Рис. 8.3

Свойства линейных операций над векторами:

1) коммутативность сложения векторов, т. е.

;

abba

+=+

2) ассоциативность сложения векторов, т. е.

(

)

(

)

;

abcabc

++=++

3) дистрибутивность сложения векторов относительно ум-

ножения на действительное число λ, т. е.

(

)

;

abab

lll

+=+

дистрибутивность сложения действительных чисел отно-

сительно умножения на вектор, т. е.

(

)

;

aaa

lmlm

+=+

4)

0;

aa

+=

5)

1;

aa

×=

6) коммутативность и ассоциативность операции умноже-

ния вектора на число, т. е.

(

)

( ) ( )

(

)

.

aaaa

lmlmmlml

===

Вектор

1

aa

-=-×

называется противоположным вектору

.

a

Разностью векторов

a

и

b

называется вектор

(

)

.

abab

-=+-

Для того чтобы найти разность

,

ab

-

векторы

a

и

b

при-

водятся к общему началу. Тогда разностью

ab

-

будет являться

вектор

,

c

у которого начало совпадает с концом вектора

,

b

а

конец – с концом вектора

a

(рис. 8.4).

Рис. 8.4

Таким образом, геометрически векторы

ab

+

и

ab

-

изо-

бражаются диагоналями параллелограмма, построенного на век-

торах

a

и

,

b

которые приведены к общему началу (рис. 8.5):

1

,

dab

=+

2

.

dab

=-

Рис. 8.5

Вектор

0

a

называется ортом (единичным вектором) век-

тора

,

a

если

0

aa

--

и

0

1.

à

=

Для его нахождения может быть

использована формула

n

аааа ++++ ...

321

2

а

3

а

n

а

1

а

О

bac -=

b

а

2

d

1

d

С

В

А

b

а

О

b

а

bac +=

О

98 99

0

.

a

=

Вектор a называется линейной комбинацией векторов

12

,,...,,

n

aaa

если существуют числа

12

,,...,,

n

ccc

такие, что

1122

...,

nn

acacaca

=+++

.

n

Î

N

Говорят, что точка C делит вектор

AB

в отношении λ

(λ > 0), если

AC

= λ

.

CB

Кроме линейных операций, для векторов определено также

скалярное умножение.

Скалярным произведением

(

)

,

ab

двух ненулевых векто-

ров

a

и

b

называется число

( )

,cos,.

ababab

Ù

æö

=××

ç÷

èø

Скалярное произведение обозначается также

.

ab

×

Если хотя бы один из векторов

a

или

b

нулевой, то

(

)

,0.

ab

=

Скалярным квадратом вектора

a

называется величина

(

)

2

,.

aaa

=

Физический смысл скалярного произведения двух векторов

состоит в том, что оно численно равно работе, осуществляемой

силой

F

по перемещению материальной точки на вектор

,

s

т. е.

(

)

sFA ,=

.

Для вычисления угла между векторами

a

и

b

можно вос-

пользоваться формулой

(

)

,

cos,.

ab

Ù

æö

=

ç÷

×

èø

Свойства скалярного произведения:

1)

(

)

(

)

abba ,, = – коммутативность;

2)

(

)

(

)

(

)

cabacba ,,, +=+ – дистрибутивность;

3)

(

)

(

)

(

)

bababa ,,,

lll

==

;

4)

(

)

,0, ãäå 0,0,

abab

=¹¹

тогда и только тогда, когда

;

ab

^

5)

(

)

0, >ba

тогда и только тогда, когда

0,,

2

ab

p

Ù

æö

£<

ç÷

èø

(

)

0, <ba

тогда и только тогда, когда

,;

2

ab

p

Ù

æö

<£

ç÷

èø

6)

, åñëè ,

(,)

, åñëè ;

abab

ab

abab

ì

×--

ï

=

í

-×-¯

ï

î

7)

(

)

(

)

2

,.

aaaa

==

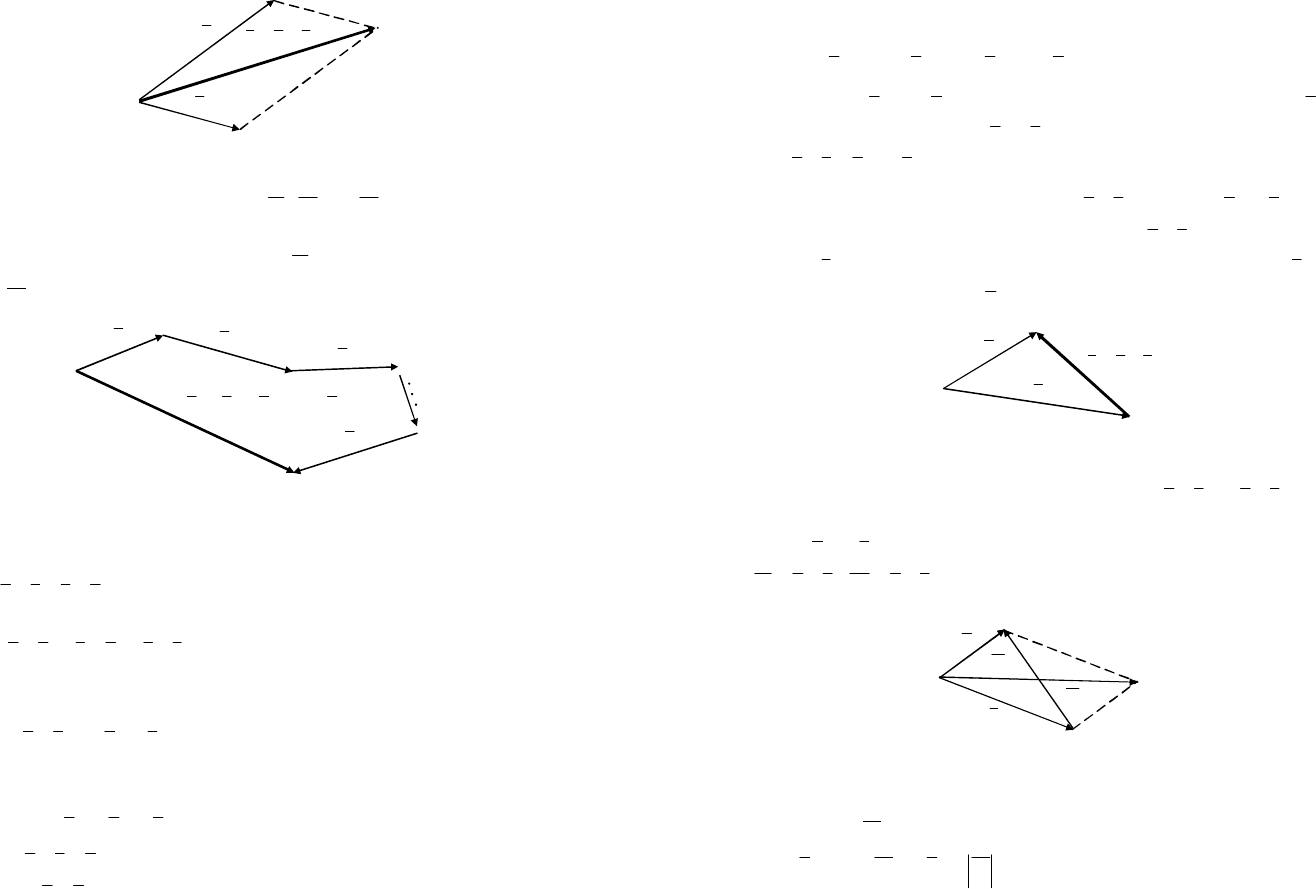
Пример 1. По заданным трем векторам

,,

abc

(рис. 8.6) изобра-

зить их линейную комбинацию

1

3.

2

dabc

=-+

Рис. 8.6

Решение. Зафиксируем на плоскости произвольную точку О и от-

ложим от нее вектор

3

a

(рис. 8.7). Затем от конца вектора

3

a

отложим

вектор

1

2

b

- и, наконец, вектор

,

c

исходящий из концевой точки век-

тора

1

.

2

b

- Искомая линейная комбинация

d

изображается вектором,

замыкающим полученную ломаную с началом в точке О.

Рис. 8.7

c

b

а

cbad +-=

2

1

3

b

2

1

-

О

c

а3

100 101

Пример 2. Найти вектор, определяющий направление биссектри-

сы угла между ненулевыми векторами

a

и

.

b

Решение. 1-й способ. Пусть для определенности

.

ab

l

=

Тогда

.

a

b

l

=

Рассмотрим векторы

a

и

1

bb

l

= с общим началом в некото-

рой точке. По определению суммы векторов вектор

1

ab

+

совпадает с

диагональю параллелограмма, построенного на векторах

a

и

1

.

b

По-

скольку

1

,

ab

=

то вектор

1

ab

+

совпадает с диагональю ромба, а

значит, с направлением биссектрисы угла между этими векторами и

векторами

a

и

.

b

Используя введенные обозначения, заключаем, что

искомое направление биссектрисы может быть задано вектором

.

a

ab

b

+

Аналогично можно показать, что вектором, задающим направле-

ние этой же биссектрисы, является также и

.

b

ab

a

+

2-й способ. Отложим от фиксированной точки плоскости единич-

ные векторы

00

11

,

aabb

ab

==

и построим на них ромб, диагональ

которого

00

ab

+=+

совпадает с направлением биссектрисы угла

между векторами

0

,

a

0

,

b

а значит, между

a

и

.

b

Пример 3. В трапеции ABCD отношение длины основания AD к

длине основания BC равно λ. Полагая

,,

ACaBDb

==

выразить через

a

и

b

векторы

,,,.

ABBCCDDA

Решение. Проведем диагонали AC и BD (рис. 8.8). Пусть О – точка

их пересечения.

Тогда из подобия треугольников AOD и COB и условия

ADBC

l

=×

следует, что

,.

AOOCODBO

ll

=×=× Имеем:

(1),îòêóäàïîëó÷àåì ;

1

a

aAOOCOCOCOCOC

ll

l

=+=×+=+×=

+

11

, îòêóäà .

1

a

aAOOCAOAOAOAO

ll

lll

+

=+=+==

+

Рис. 8.8

Аналогично из равенств

bBOOD

=+ и

ODBO

l

=× получаем:

1

(1),

bBOOD

l

+

=+= что ведет к соотношениям

,,

11

bb

BOOD

l

ll

==

++

соответственно.

Тогда, подставив найденные выражения вместо ,,

AOOBOC

и

,

OD

получим:

;

111

;

111

;

111

()

().

111

abab

ABAOOBAOBO

baab

BCBOOC

abba

CDCOODOCOD

abab

DAADAOOD

ll

lll

ll

lll

-

=+=-=-=

+++

+

=+=+=

+++

-

=+=-+=-+=

+++

æö

+

=-=-+=-+=-

ç÷

+++

èø

Пример 4. Найти угол, образованный единичными векторами

m

и

,

n

если

,

ab

^

причем

2,54.

amnbmn

=+=-

Решение. Найдем скалярное произведение векторов

a

и

,

b

ис-

пользуя его алгебраические свойства:

22

(,)(2,54)

(,5)(,4)(2,5)(2,4)

5(,)4(,)10(,)8(,)56(,)8.

abmnmn

mmmnnmnn

mmmnnmnnmmnn

=+-=

=-++-=

=-+-=+-

Из условия

ab

^

следует

(,)0,

ab

=

т. е.

b

а

D

С

В

А

О

Майсеня Л.И. Математика в примерах и задачах. Часть 2

Подождите немного. Документ загружается.