Майсеня Л.И. Математика в примерах и задачах. Часть 2
Подождите немного. Документ загружается.

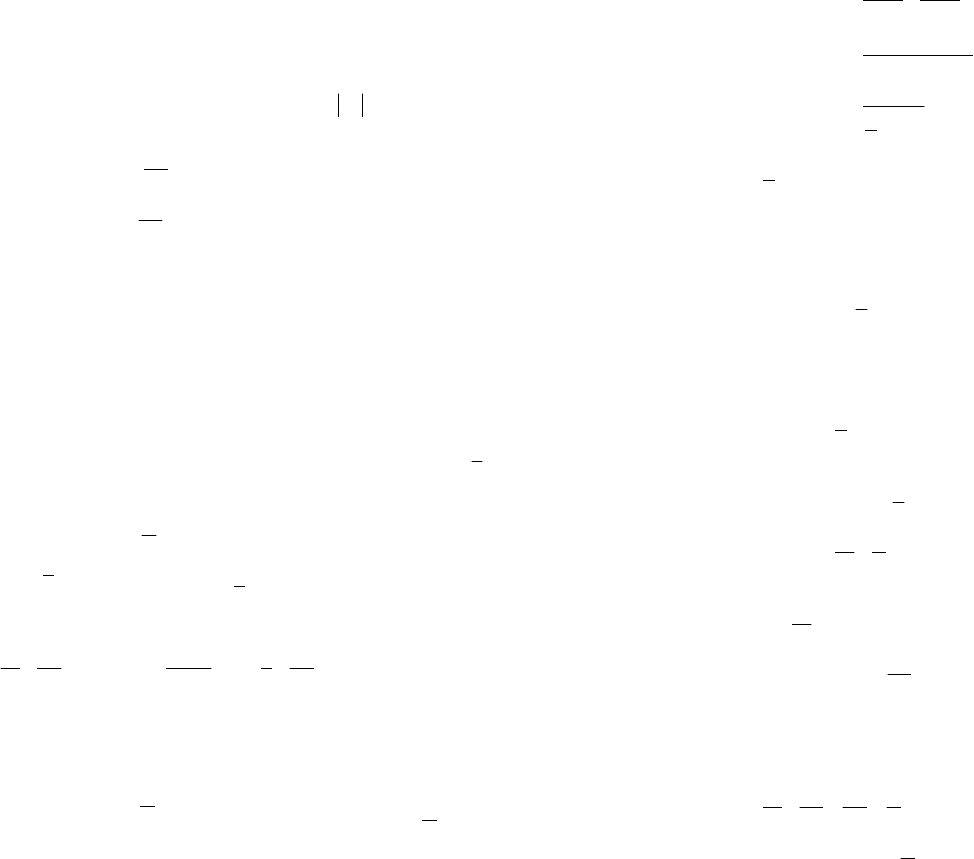
63 64
cos4.
x
Заменяем
cos4,
xy
=
получим уравнение
2
20.
yy
+-=
Его
корни
1
1
y
=
и
2
2.
y
=-
Таким образом, решение исходного уравнения
свелось к решению совокупности простейших уравнений:
cos41,
cos42.
x
x
=
é
ê
=-
ë
Уравнение
cos42
x
=-
корней не имеет, т. е.
21.
->
Решением второго является:
42, ,
xnn
p
=Î
Z
,
2
n
x
p
=
.
n
Î
Z
Получаем ответ:
,
2
n
x
p
=
.
n
Î
Z
Пример 9. Решить уравнение
2
3cos68sin3cos340.
xxx
+-=
Решение. Используем тождество
22
cos6sin61
xx
+=
и формулу
sin62sin3cos3.
xxx
=
Уравнение сводится к виду
(
)
2
31sin64sin640,
xx
-+-=
2
3sin64sin610.
xx
-+=
Мы получили квадратное уравнение относительно
sin6.
x
Заменяем
sin6,
xy
=
получим уравнение
2
3410,
yy
-+=
откуда
12
1
1; .
3
yy
==
Приходим к совокупности простейших уравнений:
( )
sin61,
62, ,
2
1
1
sin6;
61arcsin, .
3
3
k
x
xnn
x
xkk
p
p
p
é
=
=+Î
é
ê
ê
ê
ê
=
ê
=-+Î
ê
ë
ê
ë
Z
Z
Получаем ответ:
( )
1
1
, ; arcsin, .
123636
k
nk
xnxk
ppp
-
=+Î=+Î
ZZ
Пример 10. Найти сумму корней уравнения
32sin2tgctg,
xxx
+=+ если
[
]
0; .
x
p
Î
Решение.
,
ÎÄÇ:
2
,
x
xn
p
p
p
ì
¹+
ï
í
ï
¹
î
поскольку
[
]
0;,
x
p
Î
0,
,
2
.
x
x
x
p
p
¹
ì
ï
ï
¹
í
ï
¹ï
î
Упростим исходное уравнение:
22
2
2
sincos
32sin2;
cossin
sincos
32sin2;
sincos
1
32sin2;
1
sin2
2
3
sin2sin21;
2
2sin23sin220.
xx
x
xx
xx
x
xx
x
x
xx
xx
+=+
+
+=
+=
+=
+-=
Получили квадратное уравнение относительно
sin2.
x
Сделав за-
мену
sin2,
xt
=
где
11,
t
-££
имеем уравнение
2
2320,
tt
+-=
откуда
1
2
t
=-
или
2
1
.
2
t
=
Вернувшись к прежней неизвестной, получим совокупность урав-
нений:
sin2,
1
sin2.
2
x
x
=-
é
ê
ê
=
ê
ë
Первое уравнение не имеет решения. Решаем второе:
1
2(1)arcsin,;
2
n
xnn
p
=-+Î
Z
(1),.
122
n
xnn
pp
=-+Î
Z
Придаем n значение n = 0, получаем:
[ ]
0; ;
12
x
p
p
=Î
при n = 1 имеем
[ ]
5
0; .
12
x
p
p
=Î
Нетрудно убедиться, что при всех других значениях n корни не
попадут на отрезок
[
]
0; .
p
Значит сумма корней, принадлежащих от-
резку
[
]
0; ,
p
равна
56
.
1212122
pppp
+==
Получаем ответ:
.
2
p

65 66
5. Однородные уравнения
Однородным тригонометрическим уравнением n-й сте-
пени относительно sin
x
a
и
cos,
x
a
,
a
Î
R
называется уравне-
ние вида
1
01
1
1
sinsincos...
sincoscos0,
nn
nn
nn
cxcxx
cxxcx
aaa
aaa
-
-
-
+++
++=
(7.27)
где
01
,,...,
n
ccc
– действительные числа,
0
0;
c
¹
1,
n
³
.
n
Î
N
В уравнении (7.27) ,cos 0
¹
x
a
так как при 0
=
x
a
cos ис-
ходное уравнение примет вид: ,sin 0
0
=xa
n
a
откуда ,sin 0
=
x
a
что невозможно, поскольку x
a
sin и
x
a
cos
не могут одновре-
менно равняться нулю.
Разделив исходное уравнение на
cos,
n
x
a
получим:
1
011
tgtg...tg0.
nn
nn
axaxaxa
aaa
-
-
++++=
С помощью замены
tg
xt
a
=
имеем алгебраическое уравнение
1
011
...0,
nn
nn
atatata
-
-
++++=
которое решаем и возвращаемся к старой переменной.
Пример 11. Решить уравнение
2sin3cos0.
xx
-=
Решение. Разделив уравнение на
cos0,
x
¹
получим
2tg30,
x
-=
откуда
3
tg
2
x
=
и
3
arctg, .
2
xnn
p
=+Î
Z
Получаем ответ:
3
arctg,.
2
xnn
p
=+Î
Z
Пример 12. Решить уравнение
2
cos2cossincos0.
xxxx
++=
Решение. Используя формулу
22
cos2cossin,
xxx
=- приведем
данное уравнение к однородному:
222
cossincossincos0,
xxxxx
-++=
22
2cossinsincos0.
xxxx
-+=
Разделим почленно на
2
cos0:
x
¹
2
2tgtg0,
xx
-+=
откуда
2
tgtg20.
xx
--=
Введем замену
tg
xt
=
и получим уравнение
2
20,
tt
--=
корнями
которого будут
12
1; 2.
yy
=-=
После чего перейдем к решению совокупности простейших урав-
нений:
tg1,
,,
4
tg2;
arctg2,.
x
xnn
x
xnn
p
p
p
é
=-
=-+Î
é
ê
ê
ê
=
ë
=+Î
ê
ë
Z
Z
Получаем ответ:
, ; arctg2, .
4
xnnxnn
p
pp
=-+Î=+Î
ZZ
6. Неоднородные уравнения 2-й степени
Неоднородным тригонометрическим уравнением 2-й
степени называется уравнение вида
22
sinsincoscos,
axbxxcxd
aaaa
+×+=
0.
d
¹
(7.28)
Используя основное тригонометрическое тождество, приво-
дим уравнение к однородному
(
)
2222
sinsincoscoscossin,
axbxxcxdxx
aaaaaa
+×+=+
которое решаем далее как уравнение (7.27).
Пример 13. Решить уравнение
2
4sinsin23.
xx
-=
Решение. Используя формулы:
sin22sincos
xxx
= и
22
sincos1,
xx
+=
преобразуем данное уравнение к однородному:
(
)
222
4sin2sincos3cossin,
xxxxx
-=+
22
sin2sincos3cos0.
xxxx
--=
Разделим на
2
cos0:
x
¹
2
tg2tg30.
xx
--=
Введем замену
tg:
xy
=
2
230,
yy
--=
откуда
12
1;3.
yy
=-=
Решим совокупность уравнений:
tg1,
,,
4
tg3;
arctg3,.
x
xnn
x
xnn
p
p
p
é
=-
=-+Î
é
ê
ê
ê
=
ë
=+Î
ê
ë
Z
Z
Получаем ответ:
, ; arctg3, .
4
xnnxnn
p
pp
=-+Î=+Î
ZZ
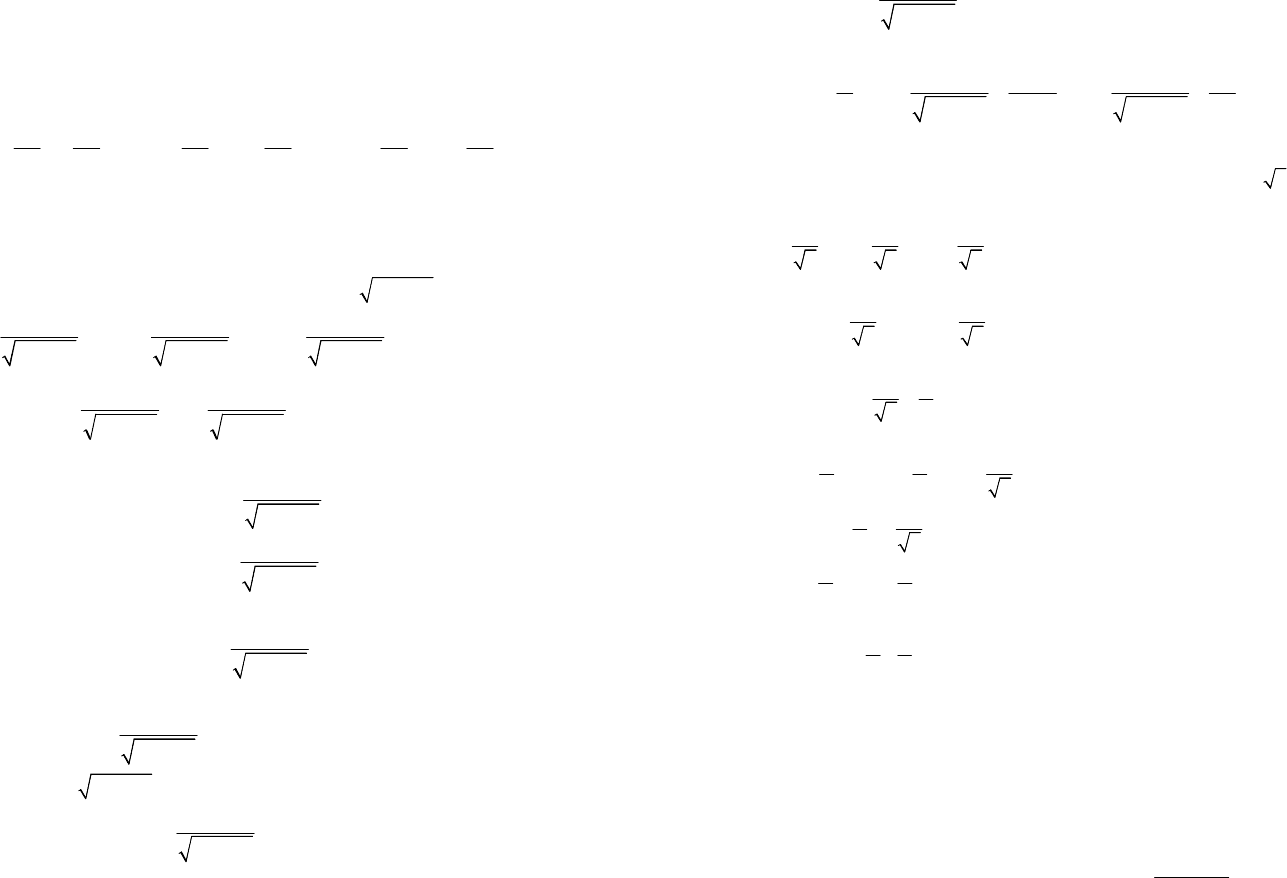
67 68
7. Неоднородные уравнения 1-й степени
Неоднородным уравнением 1-й степени называется урав-
нение вида
sincos,
axbxc
aa
+=
, , 0.
abc
¹
(7.29)
1-й способ решения. Используем формулы двойного аргу-
мента:
2222
2sincoscossinsincos.
222222
xxxxxx
abc
aaaaaa
æöæö
+-=+
ç÷ç÷
èøèø
Тогда уравнение (7.29) сводится к однородному уравнению
2-й степени, которое решаем как уравнение (7.28).
2-й способ решения. Используем метод введения вспомога-
тельного аргумента.
Разделив обе части уравнения (7.29) на
22
,
ab
+ получим:
222222
sincos.
abc
xx
ababab
aa
+=
+++
Так как ,1
2
22
2
22
=
÷
÷
ø
ö
ç
ç
è
æ
+
+
÷
÷
ø
ö
ç
ç
è
æ
+ ba
b
ba
a
то существует угол
j
,
такой, что
22
22
cos,
sin.
a
ab
b
ab
j
j
ì
=
ï
+
ï
í
ï
=
ï
+
î
(7.30)
Тогда исходное уравнение (7.29) примет вид:
22
sincoscossin
c
xx
ab
ajaj
+=
+
или, используя формулу (7.8) для синуса суммы, получим:
( )
22
sin.
c
x
ab
aj
+=
+
Если
22
,
cab
£+ то последнее уравнение имеет решение:
( )
22
1arcsin, .
k
c
xkk
ab
ajp
+=-+Î
+
Z
Угол
j
находят из формулы (7.30), например,
22
arccos.
a
ab
j
=
+
Приходим к ответу:
( )
2222
1
1
arccosarcsin, .
k
ack
xk
abab
p
aaa
-
=-++Î
++
Z
Пример 14. Решить уравнение
sincos1.
xx
+=
Решение. Разделив левую и правую часть уравнения на
2
(так
как
1; 1
ab
==
), получим:
111
sincos.
222
xx+=
Тогда
1
cos
2
j
= и
1
sin,
2
j
=
откуда
1
arccos.
4
2
p
j
==
Таким образом, получаем уравнение:
1
cossinsincos,
44
2
xx
pp
+=
1
sin,
4
2
x
p
æö
+=
ç÷
èø
()
1, ,
44
k
xkk
pp
p
+=-+Î
Z
откуда приходим к ответу:
( )
1, .
44
k
xkk
pp
p
=--+Î
Z
8. Уравнения, решаемые с применением формул
понижения степени
При решении широкого круга тригонометрических уравне-
ний ключевую роль играют формулы понижения степени (7.12).
Пример 15. Решить уравнение
2222
sinsin2sin3sin40.
xxxx
+++=
Решение. Используем формулу
2
1cos2
sin.
2
a
a
-
=
Заданное
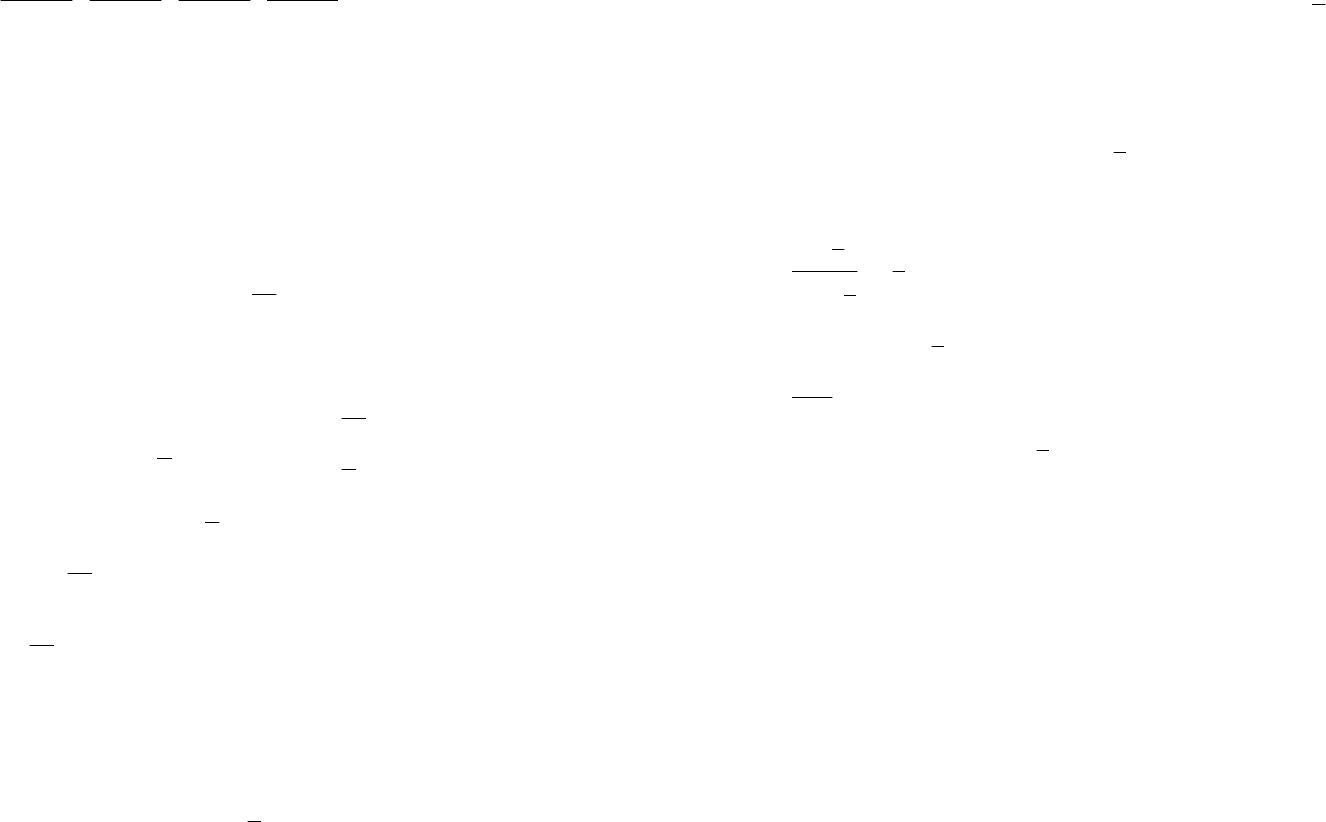
69 70
уравнение примет вид:
1cos21cos41cos61cos8
0.
2222
xxxx----
+--=
Преобразуя, перейдем к решению уравнения
cos8cos6cos2cos40,
xxxx
+--=
откуда
(
)
(
)
cos8cos2cos6cos40.
xxxx
-+-=
Применив формулы (7.13) преобразования суммы и разности ко-
синусов в произведение, получим:
2sin3sin52sinsin50
xxxx
--=
или
(
)
2sin5sin3sin0,
xxx
+=
откуда
sin50; 5, ; , ;
5
n
xxnnxn
p
p
==Î=Î
ZZ
sin3sin0;
xx
+=
2sin2cos0.
xx
=
Получаем совокупность уравнений:
2,,
,,
sin20,
2
cos0;
,;
,.
2
2
k
xkk
xk
x
x
xnn
xnn
p
p
p
p
p
p
é
=Î
=Î
é
ê
=
é
ê
ê
ê
ê
=
=+Î
ë ê
=+Î
ê
ë
ê
ë
Z
Z
Z
Z
Множество решений
,
2
xnn
p
p
=+Î
Z
содержится во множестве
решений
, .
2
k
xk
p
=Î
Z
Поэтому приходим к ответу:
, .
2
k
xk
p
=Î
Z
9. Уравнения, решаемые методом универсальной
подстановки
Тригонометрическое уравнение, рациональное относительно
sin,
x
cos,
x
tg,
x
ctg,
x
может быть сведено к рациональному
уравнению относительно
tg
2
x
t = с помощью формул универ-
сальной подстановки (7.15).
Следует отметить, что применение формул (7.15) может
привести к сужению ОДЗ исходного уравнения, поскольку
tg
2
x
не определен в точках
2,
xn
pp
=+
.
n
Î
Z
Поэтому в таком слу-
чае нужно проверять, являются ли значения
2,
xn
pp
=+
,
n
Î
Z
корнями исходного уравнения.
Пример 16. Решить уравнение
sintg0.
2
x
x
+=
Решение. По условию задачи
2,
xk
pp
¹+
.
k
Î
Z
Применим фор-
мулу (7.15) и преобразуем уравнение к виду
2
2tg
2
tg0.
2
1tg
2
x
x
x
+=
+
Сделав замену
tg,
2
x
t
=
получим:
2
2
0,
1
t
t
t
+=
+
откуда
0
t
=
и, следовательно,
tg0.
2
x
=
Решая последнее уравнение,
получаем ответ:
2,
xk
p
=
.
k
Î
Z
10. Уравнения, решаемые применением ограниченности
тригонометрических функций
Рассмотрим уравнения, решение которых основано на сле-
дующем утверждении: если при решении уравнения
(
)
(
)
fxgx
=
удалось установить, что для всех допустимых значений пере-
менной х выполняется
(
)
fxa
£
и
(
)
gxa
³
(а – константа), то
данное уравнение равносильно системе
(
)
()
,
.
fxa
gxa
ì
=
ï
í
=
ï
î
При решении уравнений, содержащих тригонометрические
функции
sin,
x
cos,
x
надо помнить, что
1sin1
x
-££
и
1cos1.
x
-££
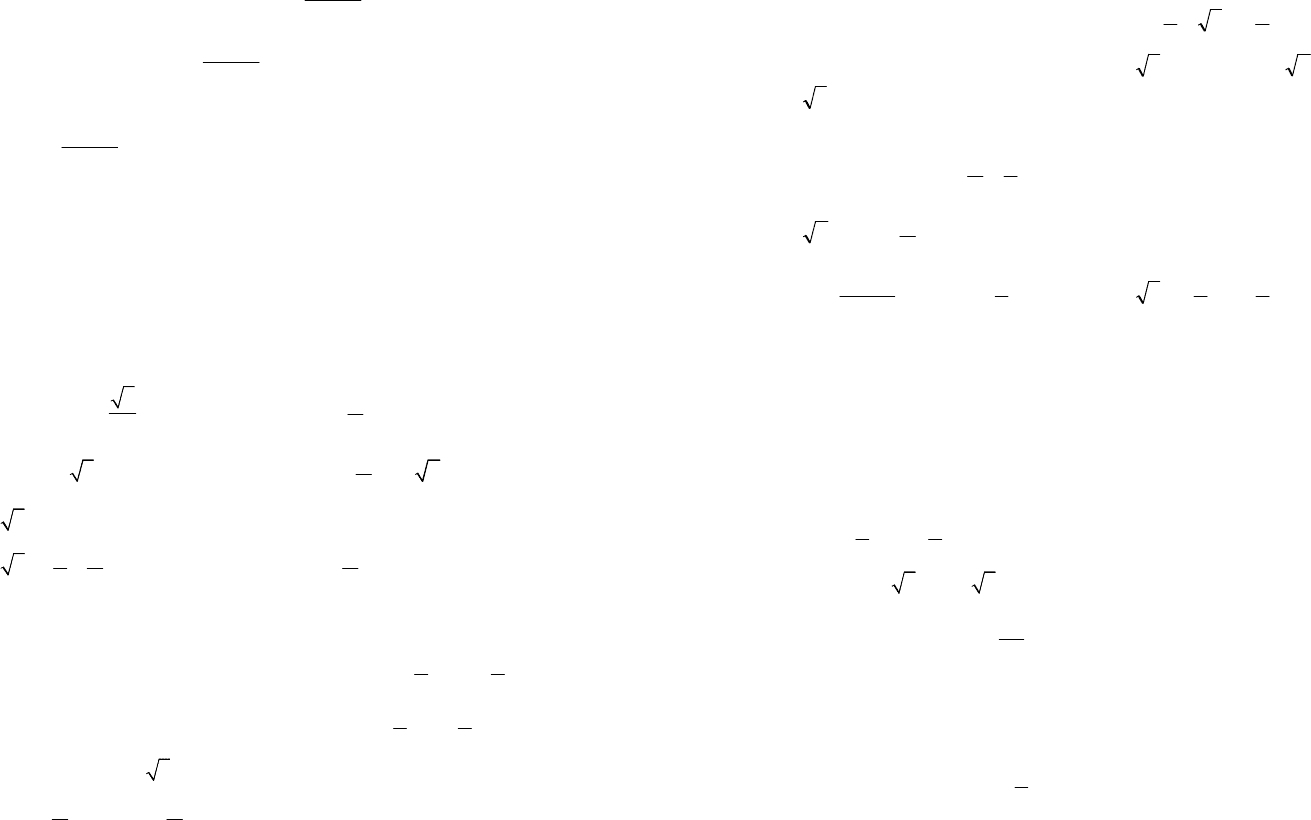
71 72
Пример 17. Решить уравнение
2
2
8
cos1.
5
xx
x
æö
-
=+
ç÷
ç÷
èø
Решение. Так как
2
8
cos1,
5
xx
æö
-
£
ç÷
ç÷
èø
а
2
11,
x
+³
то данное уравне-
ние равносильно системе
2
2
8
cos1,
5
11,
xx
x
ì
æö
-
=
ï
ç÷
ç÷
í
èø
ï
+=
î
имеющей единственное решение
0.
x
=
Получаем ответ:
0.
x
=
Задания
I уровень
1.1. Решите тригонометрическое уравнение:
1)
3
cos(2);
2
x-=- 2)
cos20;
4
x
p
æö
-=
ç÷
èø
3)
2sin30;
x
+=
4)
2sin32;
4
x
p
æö
-=-
ç÷
èø
5)
3tg10;
x
-=
6)
ctg10;
x
+=
7)
3tg3;
33
x
p
æö
+=
ç÷
èø
8)
ctg30.
4
x
p
æö
-=
ç÷
èø
1.2. Решите уравнение:
1)
;sinsin 0102515
2
=-- xx
2)
;coscos 0
2
1
2
1
2
=-- xx
3)
2
tg24tg230;
xx
-+=
4) ;cossin 06
2
2
5
2
=-+
xx
5)
tg33tg323;
xx+= 6)
;cossin 02
=
-
xx
7) ;coscos 1
44
=
÷
ø
ö
ç
è
æ
-+
÷
ø
ö
ç
è
æ
+ xx
pp
8)
;cossin 03
=
+
xx
9) ;sincoscos xxx 435333
=
-
10) ;sincos 022
2
=+ xx
11)
;sinsinsin 032
=
+
+
xxx
12)
;cossinsin xxx 23
=
13) ;cossin xx 222
=
14) ;cossin 0
4
3
4
=+
xx
15) ;cossinsin xxx 23
=
16) ;cossin 23 =+ xx
17) ;cossin 2223 =- xx 18) ;sin 0124
2
=-x
19)
;sinsinsin xxx 32
222
=+
20)
;cos 14
2
=x
21)
( )
;sincos 0
22
1 =
÷
ø
ö
ç
è
æ
++--
x
x
p
p
22) ;sincos xx 221
42
=+
23)
( )
;cossincos
2
4
2 xxx +=
÷
ø
ö
ç
è
æ
-
p
24) ;sinsin xx 33
=
25)
5
3ctg6ctg3;
22
xx
p
p
-
æö
+-=
ç÷
èø
26) ;sincos 1
2
2
3 =+
xx
27) ;coscoscoscos xxxx 735
+
=
+
28)
2
3cos2sin5sincos0.
xxxx
++=
II уровень
2.1. Решите уравнение:
1) ;sinsin 324
2
=- xx
2)
;sincos 0
3
3
3
2
2
=+
xx
3)
(
)
2
tg13tg30;
xx
-++=
4)
( )
( )
3
tg245tg2;
2
xx
p
p
æö
++=-
ç÷
èø
5) ;sinsin 024
2
=+ xx
6) ;coscoscos xxx 243
=
+
7) ;sinsincos 024432
22
=++ xxx
8) ;sincoscoscossin xxxxx 12
4
1
82 =
9) ;sin,cossin xxx 4522322
22
=+
10) ;sin,sincos xxx 651332
22
=+
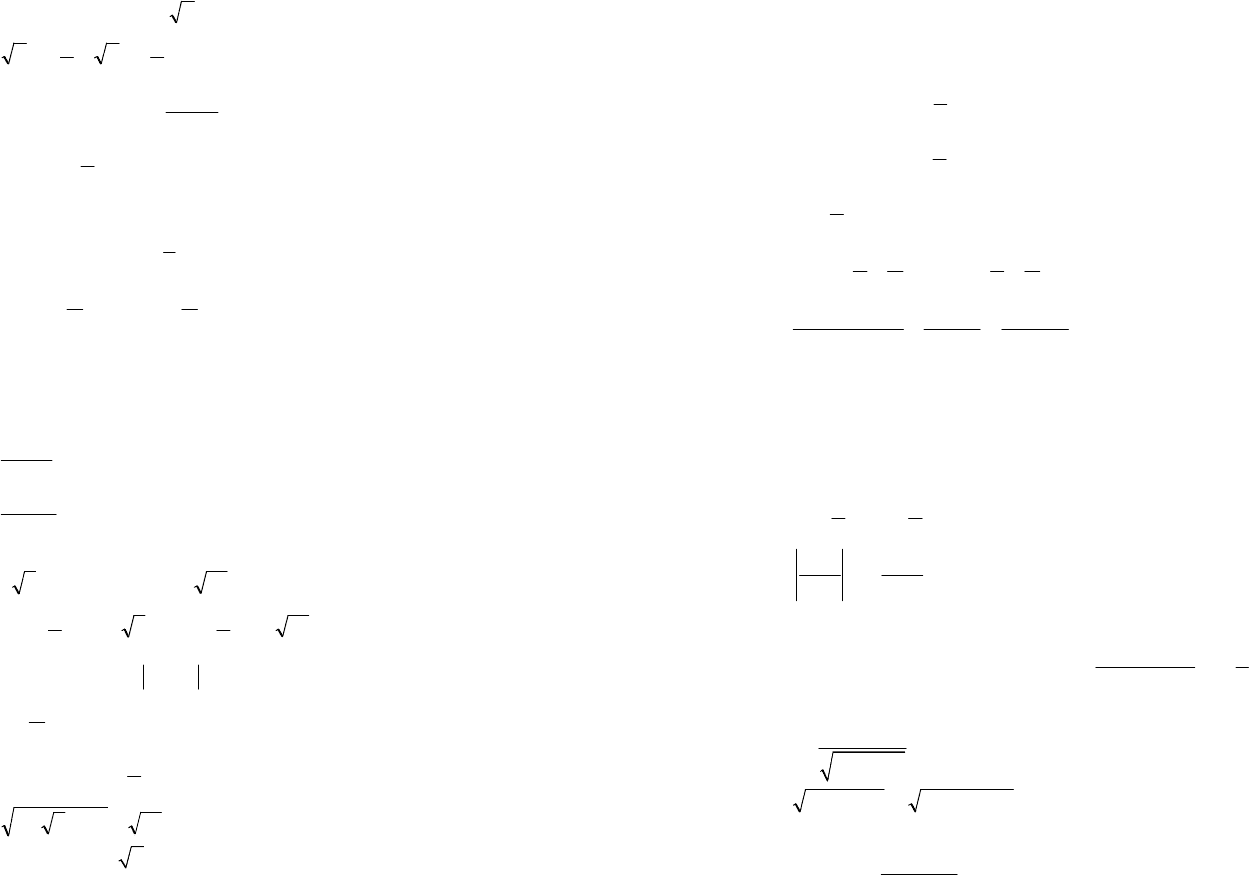
73 74
11) ;cossin 26262 =+ xx
12) ;sincos 1
4
2
4
2 =-
xx
13) ;
sin
cossin
2
2
1
33
x
xx +=-
14) ;cossin 12
4
1
2
32
=+ xx
15) ;sincossin xxx 4132
22
+=+
16) ;cossin
8
5
22
44
=+ xx
17)
;coscossin xxx 21
36
+=
÷
ø
ö
ç
è
æ
++
÷
ø
ö
ç
è
æ
+
pp
18) ;sincos 3232
=
+
xx
19)
32
tgtg2tg20;
xxx
+--=
20) ;sinsin 224
24
=+ xx
21) ;
sin
sin
0
3
=
x
x
22)
;
cos
cos
0
7
=
x
x
23) ;sinsincos xxx
-
=
+
341
24) ;sincos 1266632 =+ xx
25) ;cossin 12
3
232
3
3 -=
÷
ø
ö
ç
è
æ
-+
÷
ø
ö
ç
è
æ
-
xx
26)
cos2cos6cos4;
xxx
+=
27) ;sin 54
4
2
+-= xxx
p
28) ;cos
x
xx
1
22 +=
p
29) ;cossin 01031 =+- xx
30)
(
)
sincos2tgctg.
xxxx
+=+ Найдите сумму корней уравне-
ния на отрезке
[
]
.;
p
3 0
III уровень
3.1. Решите уравнение:
1)
;sincos 1532
2
=+ xx
2) ;sincossin xxx 2
2
1
44
=+
3) ;cossin
4
1
66
=+ xx
4)
;cossin 045
2
4
=++ x
x
5) ;sincos 4
84
6
42
4
22
=
÷
ø
ö
ç
è
æ
++
÷
ø
ö
ç
è
æ
+
pp
xx
6)
2
sin418
;
sin3costg3
tg9
x
xxx
x
+=
-+
-
7)
22
ctg2ctg24tg2tg2;
xxxx
+=-+
8) ;sincossin xxx 254232
2
=-+
9) ;sinsincos xxx
44
243 =-+
10) ;cossincos xxx
33
2 -=
11) ;cossin 5
2
4
2
3 =-
xx
12) .
sinsin xx
11
-= Найдите наименьшее целое решение урав-
нения, удовлетворяющее условию
[
]
180; 90;
x
Î-°-°
13) Найдите все решения уравнения
cossin
tg,
cossin2
xxx
xx
-
=
+
удовле-
творяющие условию ;cossin 0
<
xx
14)
2
2
1
12cos;
1ctg
x
x
+=
+
15) ;cossin xx 24141 -=-
16)
sin2cos2tg;
xxx
-=
17)
cos2
2tg2;
1sin2
x
x
x
-=
+
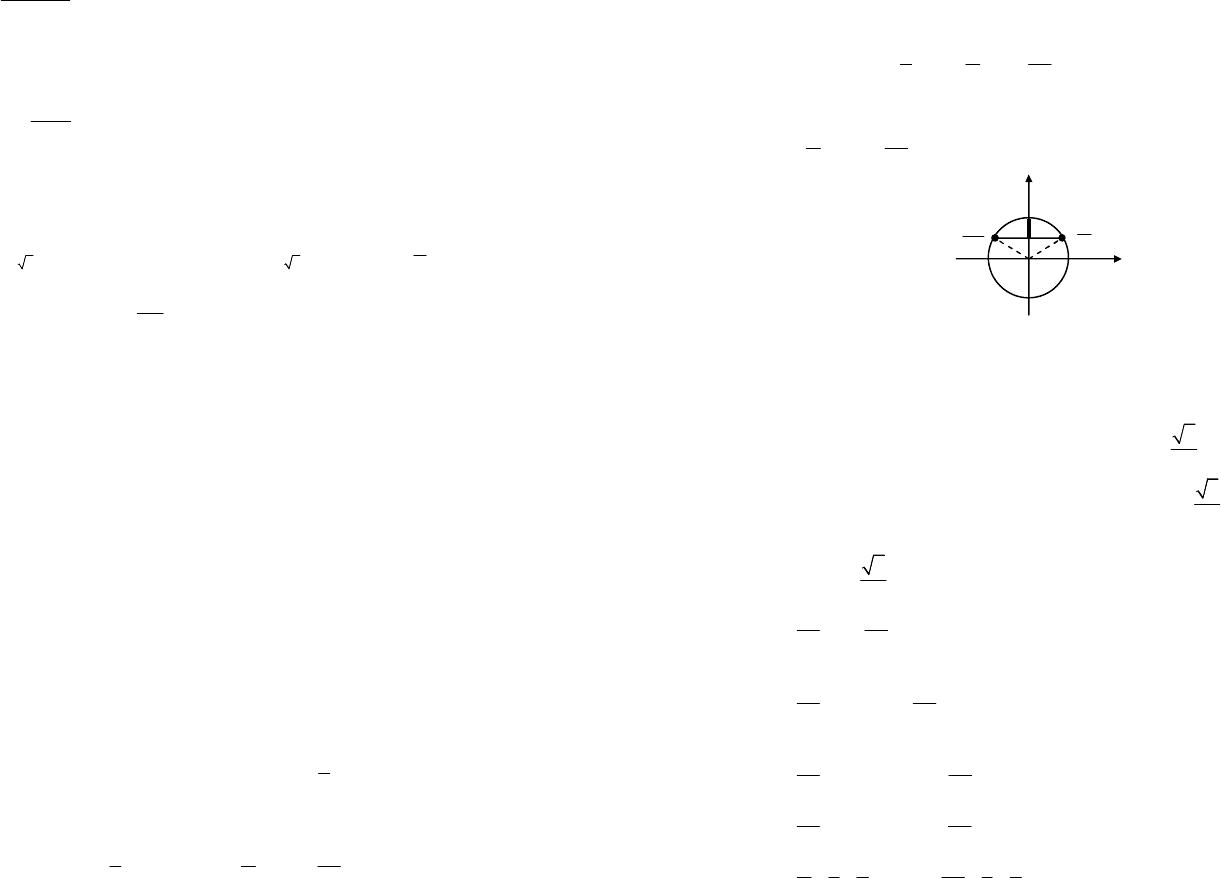
75 76
18)
1cos
3;
1sin
x
x
+
=
-
19)
(
)
(
)
2
2sincos1cossin.
xxxx
+×-=
Найдите сумму корней
уравнения, принадлежащих отрезку
[
]
;;
pp
-
20)
1
1cosctg.
sin
xx
x
+=+
Найдите количество корней, принад-
лежащих промежутку
[
]
.;
pp
4 6-
3.2. Решите уравнение:
1)
(
)
2cos
log1sin2;
x
x
+=
2)
2sin0,5
log1cos2;
2
x
x
æö
+=
ç÷
èø
3)
2
452
21sin;
4
xx
x
p
-+
=+ 4)
(
)
2
3331cos2.
xx
x
p
-
+=+
3.3. Найдите все значения параметра а, при которых уравне-
ние имеет хотя бы одно решение:
1)
2
cos1(1);
axa+=+ 2)
2
2cos214cos2;
axax
+=-
3)
22cos234sin.
xax
-=+
7.6. Тригонометрические неравенства
Для решения тригонометрических неравенств используют
единичную окружность и определение тригонометрических функ-
ций или графический метод, а также метод замены переменной.
Простейшие тригонометрические неравенства
и неравенства, сводящиеся к ним
Пример 1. Решить неравенство
1
sin.
2
x
>
Решение. Воспользуемся определением синуса. С помощью еди-
ничной окружности находим вначале углы х, которые соответствуют
равенству
1
sin.
2
x
=
Их два:
6
x
p
=
и
5
6
x
p
= (рис. 7.25). Строим их,
причем соответствующие радиус-векторы пунктиром, так как заданное
неравенство строгое.
Выделим на единичной окружности множество точек, ординаты
которых больше
1
,
2
это
5
.
66
x
pp
<< Используя периодичность функ-
ции
(
)
sin,
fxx
= приходим к ответу:
5
2; 2,
66
kk
pp
pp
æö
++
ç÷
èø
.
k
Î
Z
Рис. 7.25
Ответ неравенства следует понимать как объединение всех про-
межутков, которые получаем при всех
.
k
Î
Z
Пример 2. Решить неравенство
( )
2
cos31.
2
x +£-
Решение. Заменив 3x + 1 на t, получим:
2
cos.
2
t £- Выделим на
единичной окружности множество точек, абсциссы которых меньше
или равны
2
2
-
(рис. 7.26). Получим:
35
.
44
t
pp
££
Учитывая период, имеем:
35
22.
44
ktk
pp
pp
+££+
Возвращаемся к заданной неизвестной:
35
2312;
44
kxk
pp
pp
+£+£+
35
12312;
44
kxk
pp
pp
-+££-+
12512
,
4331233
kxk
pp
pp
-+££-+
.
k
Î
Z
1
1
6
5
p
6
p
х
у
0
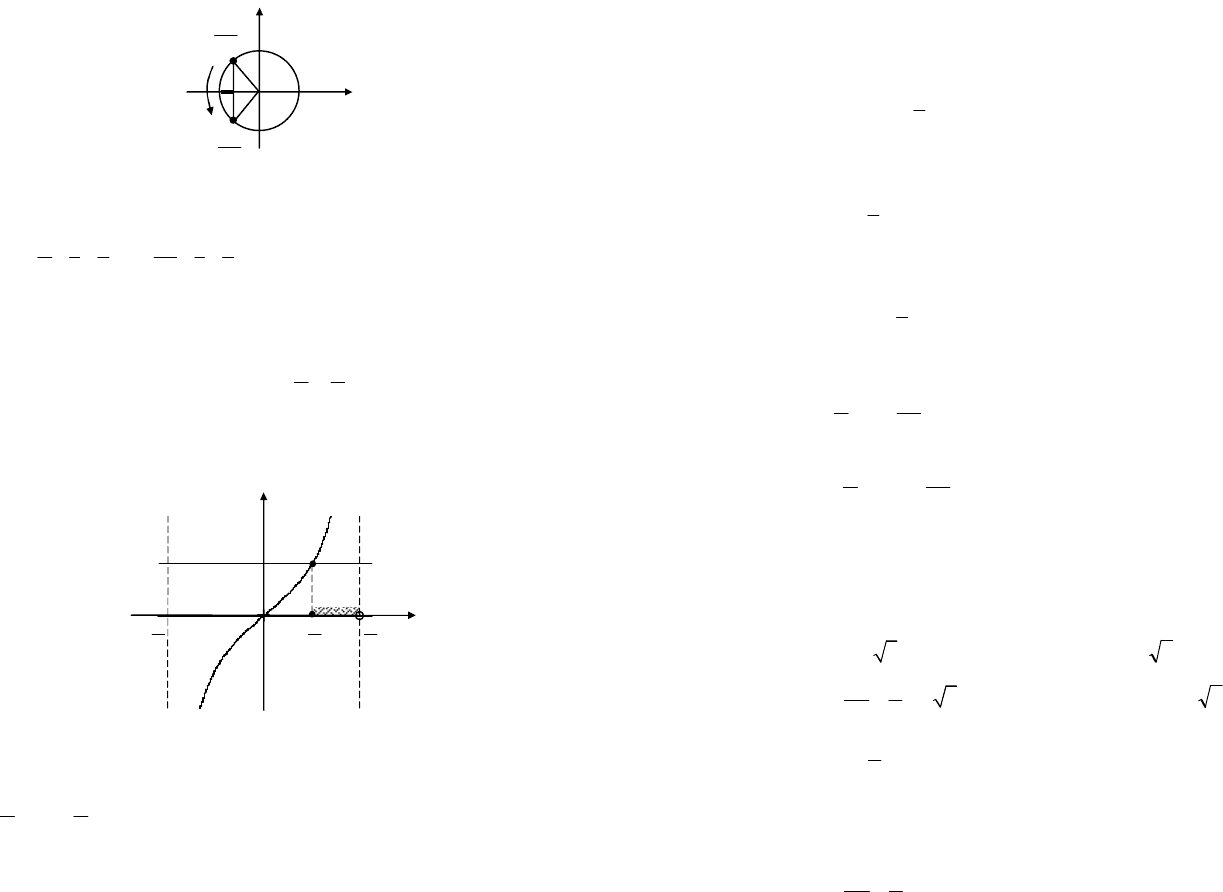
77 78
3
4
p
5
4
p
0
х
у
Рис. 7.26
Приходим к ответу:
12512
; ,
4331233
kk
pp
pp
éù
-+-+
êú
ëû
.
k
Î
Z
Пример 3. Решить неравенство
tg1.
x
³
Решение. Используем графический метод. Построим график
функции
tg
yx
=
для промежутка
; .
22
pp
æö
-
ç÷
èø
Проведем прямую
1
y
=
(рис. 7.27). Находим промежуток оси абсцисс, для точек которого гра-
фик
tg
yx
=
проходит не ниже построенной прямой. Этот промежуток
и будет решением неравенства на рассматриваемом интервале.
Рис. 7.27
С учетом периодичности функции
tg
yx
=
приходим к ответу:
; ,
42
kk
pp
pp
éö
++
÷
ê
ëø
.
k
Î
Z
Пример 4. Решить неравенство
5sincos23.
xx
-+<
Решение.
(
)
2
5sin12sin3;
xx
-+-<
2
2sin5sin20.
xx
++>
Заменим
sin.
xt
=
Имеем:
2
2520,
tt
++>
( )
1
220,
2
tt
æö
++>
ç÷
èø
т. е. получаем:
2,
1
.
2
t
t
<-
é
ê
ê
>-
ê
ë
Возвращаемся к старой переменной:
sin2,
1
sin.
2
x
x
<-
é
ê
ê
>-
ê
ë
Первое неравенство совокупности решения не имеет. Решаем вто-
рое. С помощью единичной окружности получаем:
7
.
66
x
pp
-<<
Учитываем период и приходим к ответу:
7
2; 2,
66
kk
pp
pp
æö
-++
ç÷
èø
.
k
Î
Z
Задания
I уровень
1.1. Решите неравенство:
1)
3tg3;
x-³ 2) ;cos 32 ³x
3)
3
ctg3;
22
x
p
æö
-£
ç÷
èø
4)
(
)
;sin 332 £+ x
p
5)
tg10;
3
x
p
æö
++³
ç÷
èø
6)
sin40.
x
+£
II уровень
2.1. Решите неравенство:
1)
3
ctg10;
22
x
p
æö
+-£
ç÷
èø
2) ;sinsin 02
2
<+ xx
4
p
2
p
2
p
-
0
у
= 1
у
1
х
у = tg x
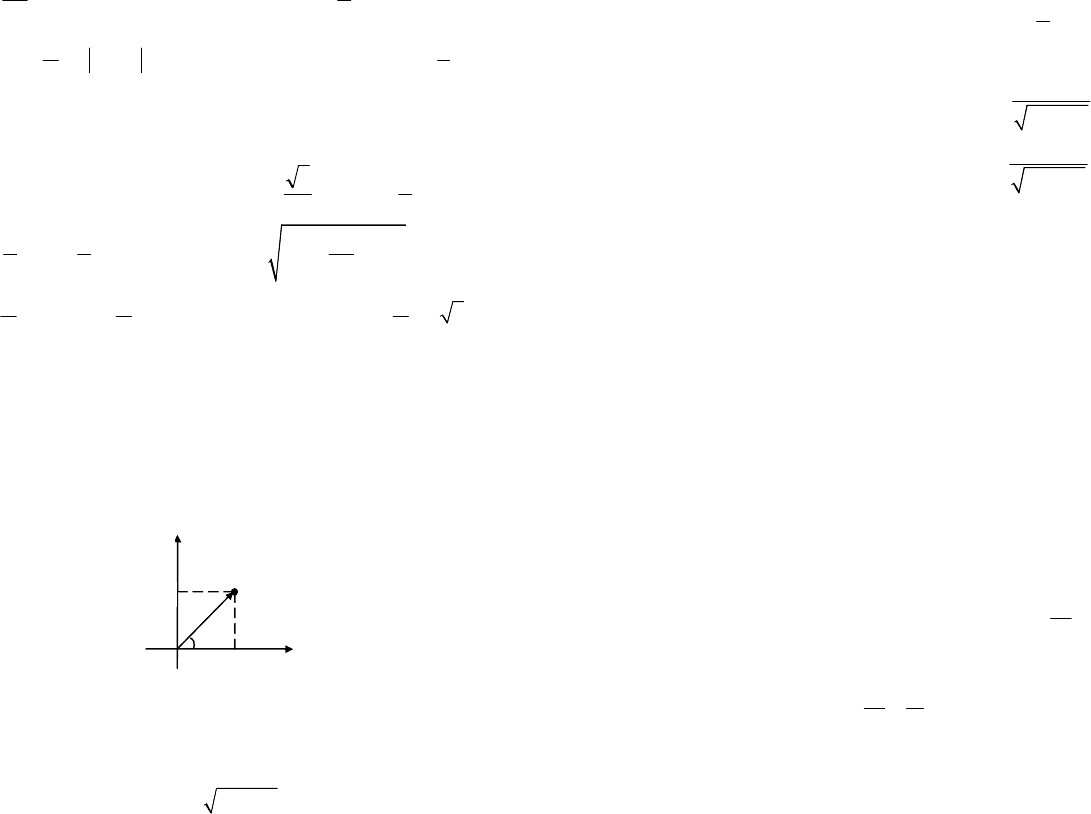
79 80
3) ;,cos 0504
4
3
>+
÷
ø
ö
ç
è
æ
- x
p
4) ;sin 3
2
4 ³
x
5)
2
cossin230;
4
xx
p
æö
++-³
ç÷
èø
6) .sincos
8
5
44
£+ xx
III уровень
3.1. Решите неравенство:
1)
2
2tg210;
x
->
2)
;cos
3
2
2
3
<£- x
3)
;,sincos 50
3
3
22
-£
xx
4)
2
3
sin240;
2
x
p
æö
-+£
ç÷
èø
5)
sincos3;
36
xx
pp
æöæö
-+-³
ç÷ç÷
èøèø
6)
4coscos3.
6
xx
p
æö
+>
ç÷
èø
7.7. Тригонометрическая и показательная формы
комплексного числа
Комплексное число
zaib
=+
в прямоугольной декартовой
системе координат Оху изображается точкой М (рис. 7.28).
Рис. 7.28
Длина радиус-вектора точки М называется модулем ком-
плексного числа z и обозначается |z| или r:
22
.
rab
=+ (7.31)
Угол
j
, образованный этим вектором с положительным на-
правлением действительной оси Ох, называется аргументом
числа z. Связь между аргументом
j
комплексного числа и его
действительной и мнимой частью выражается формулами:
tg
b
a
j
=
(7.32)
или
22
22
cos,
sin.
a
ab
b
ab
j
j
ì
=
ï
+
ï
í
ï
=
ï
+
î
(7.33)
Аргумент комплексного числа определен неоднозначно: ес-
ли
j
– аргумент числа z, то
k
p
j
2
+
– также аргумент этого чис-
ла при любом целом k. Для однозначности определения аргу-
мента его выбирают в пределах
p
j
p
£
<
-
[
)
(
)
èëè 0;2,
p
та-
кое значение аргумента называют главным и обозначают
.
arg
z
Всюду далее будем рассматривать главное значение аргумента:
arg.
z
j
=
На практике находить аргумент комплексного числа z имеет
смысл согласно формуле (7.32) с учетом координатной четверти,
в которой лежит число z, или формул (7.33).
Запись комплексного числа в виде
)sin(cos
j
j
irz
+
=
(7.34)
называется тригонометрической формой комплексного числа.
Пусть
1111
(cossin)
zri
jj
=+
и
2222
(cossin)
zri
jj
=+
ком-
плексные числа, заданные в тригонометрической форме. Тогда
для произведения
12
zz
×
и частного
1
2
z
z
справедливы формулы:
12121212
(cos()sin()),
zzrri
jjjj
×=+++
(7.35)
( ) ( )
( )
11
1212
22
cossin.
zr
i
zr
jjjj
=-+-
(7.36)
Для комплексного числа
(cossin)
zri
jj
=+
справедлива
формула Муавра:
(cossin),.
nn
zrninn
jj
=+Î
N
(7.37)
Корнем n-й степени из комплексного числа z называется
комплексное число w такое, что
.
n
wz
=
Корень n-й степени из комплексного числа
M
a
0
x
y
b
j

81 82
)sin(cos
j
j
irz
+
=
имеет n различных значений, которые находят по формуле
( )
22
cossin,
nn
k
k
kk
wzri
nn
jpjp
++
æö
==+
ç÷
èø
(7.38)
где
0,1,2,...,1;
kn
=-
n
r
– арифметическое значение корня.
Все значения корня
(
)
,
k
n
z
,, 10 -= nk
расположены на ок-
ружности с центром в начале системы координат и радиусом
n
r
в вершинах правильного вписанного в окружность n-угольника.
Соотношение
cossin
i
ei
j
jj
=+ (7.39)
называется формулой Эйлера.
Пусть комплексное число z записано в тригонометрической
форме. Используя формулу Эйлера (7.39), можно записать:
.
j
i
rez = (7.40)
Такая форма записи называется показательной формой
комплексного числа.
Правила действий над комплексными числами
в показательной форме
12
()
1212
;
i
zzrre
jj
+
= (7.41)
12
()
11
22
;
i
zr
e
zr
jj
-
=
(7.42)
;
nnin
zre
j
=× (7.43)
( )
2
,
k
i
nn
n
k
k
wzre
jp
+
×
==×
где
0;1.
kn
=-
(7.44)
Пример 1. Представить в тригонометрической форме комплекс-
ное число:
1)
443;
zi
=- 2)
3;
zi
=-
3)
13.
z =-
Решение. 1) Находим модуль данного числа по формуле (7.31):
22
4(43)8.
z
=+=
Для нахождения аргумента
j
используем формулу (7.32):
tg3
j
=-
и число z лежит в IV четверти. Поэтому
3
p
j
=-
(рис. 7.29).
Рис. 7.29
Подставим полученные значения |z| и
j
в формулу (7.34), получим:
8cossin.
33
zi
pp
æö
æöæö
=-+-
ç÷
ç÷ç÷
èøèø
èø
2) В данном случае
3,
z
=
2
p
j
=-
(точка, изображающая данное
число, принадлежит отрицательной части мнимой оси (рис. 7.30)).
Рис. 7.30
Поэтому
3cossin.
22
zi
pp
æö
æöæö
=-+
ç÷
ç÷ç÷
èøèø
èø
3) Находим модуль комплексного числа
( )
2
2
1301331
z
=-+=-=-
(так как
130
-<
),
jp
=
(заданное число является отрицательным
действительным числом (рис. 7.31)).
Рис. 7.31
Поэтому
(
)
31(cossin).
zi
pp
=-×+
z
4
0
x
y
r
j
43
-
–3
0
x
y
j
13
-
0
x
y
j
