Маркин П.М. Математическая логика
Подождите немного. Документ загружается.

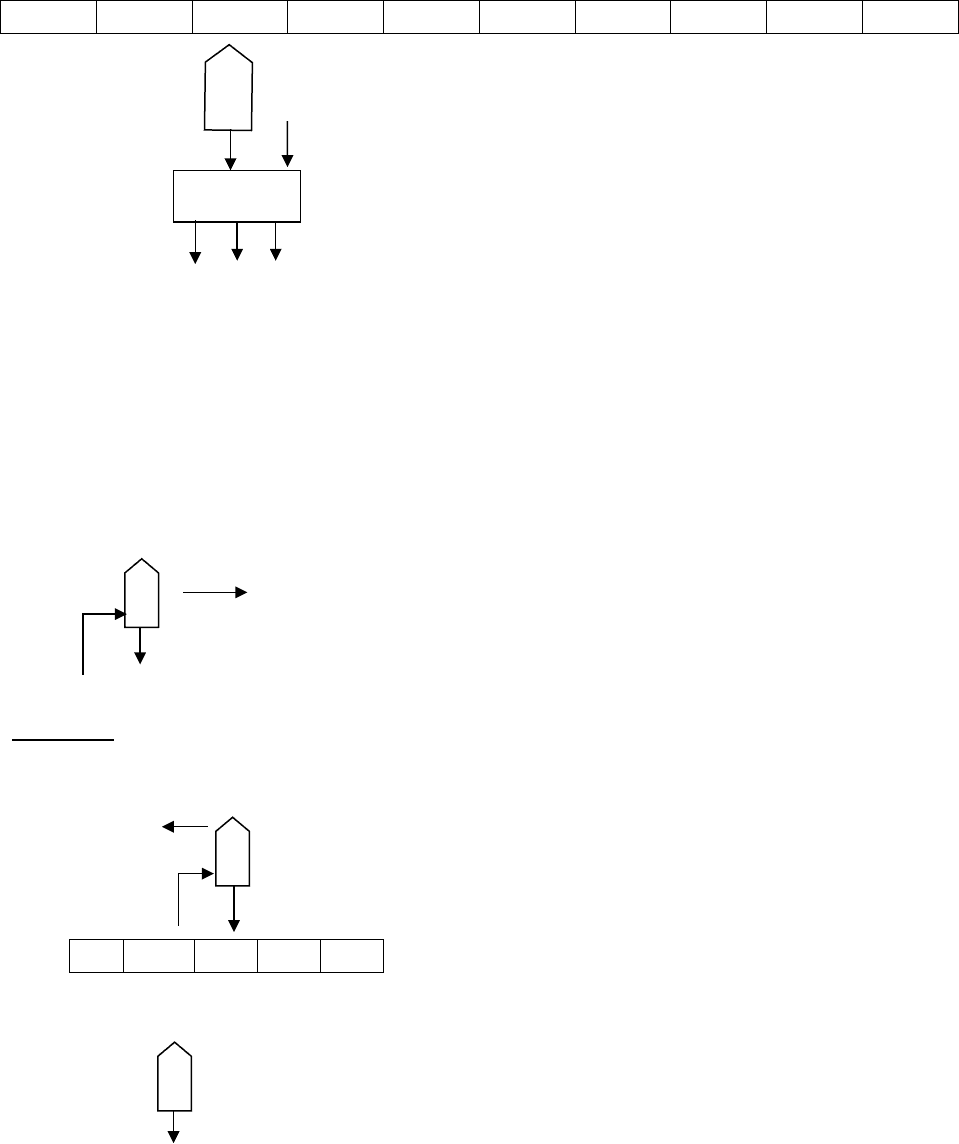
д) Начальная атрибуция (конфигурация машины) характеризуется
следующим образом:
1) на ленте записано слово А
*
;
2) управляемая головка указывает на ячейку ленты, в которой записан
самый левый символ цепочки (слова),
3) машина находится в начальном состоянии q
0
Q;
Пример начальной конфигурации машины:
a
0
a
0
a
2
a
4
a
7
a
3
a
9
a
0
a
0
a
0
Символически эта конфигурация записывается как машинное слово
q
0
= q
0
a
2
a
4
a
7
a
3
a
9
= k
0.
e) Текущая (порожденная) ситуация (конфигурация) k
p
есть машинное слова
вида
1
q
j
a
i
2
, где
1
и
2
– цепочки символов алфавита А.
ж) Заключительная ситуация (конфигурация) k
z
имеет вид q
z
, где q
z
–
заключительное состояние машины, q
z
Q, - результат работы машины из
исходной ситуации по заданной программе, А
*
.
Очевидно, что последовательность конфигураций k
0
k
2
k
2
… однозначно
определяется исходной конфигурацией k
0
и полностью описывает работу
машины Тьюринга Т= =<A, Q, q
0
, q
z
, >, начиная с k
0
= q
0
(А
*
исх
, А
исх
А).
Эта последовательность конечна, если в ней встретится заключительная
конфигурация k
z
= q
z
, и бесконечна в противном случае.
Пример:
1) Пусть последовательность k0 k2 kz имеет вид q0 a2 a1 a4 q1 a1 qz
a4 a2 (очевидно, что последовательность команд следующая: q0 a2 q1 a4
dп, q1 a1 qz a2 dЛ).
Имеем следующую интерпретацию смены ситуаций:
k
0
a
0
a
2
a
1
a
0
a
0
51
a
2
БУ
q
0
q
0
d
п
а
2
а
4
d
Л
а
2
а
1
q
1
а
4
q
z

k
1
k
z
2) Машина Т=<a
0
, a, q
0
, q
z
, q
0
a
0
q
0
a d
п
, q
0
a q
0
a d
п
> будет работать
бесконечно, заполняя все ячейки ленты символами а вправо от начальной
пустой ячейки (исходная информация на ленте - пустые символы а
0
в каждой
ячейке ленты).
Примечания:
1) Соответствие, устанавливаемое машиной Тьюринга между теми
исходными данными, к которым она применима ( то есть она
приводит к результату) и результатами ее работы представляет собой
некоторую словарную функцию (в математическом смысле)
Т(
*
исх
*
рез
исх
рез
пром
.
2) Если для функции имеется машина ее реализующая, то говорят, что
эта функция вычислима по Тьюрингу. Функция, для вычисления
которой существует алгоритм, называется вычислимой.
3) Поскольку слово (
*
, m) можно отождествить с натуральным
числом (в m-ичной системе счисления), то уточнение понятия
вычислимой словарной функции приводит и к уточнению понятия
вычислимой числовой функции f:N
k
N, kN. Тьюринг доказал. что
класс числовых функций, вычислимых на машине Тьюринга,
совпадает с классом частично-рекурсивных функций.
Формальное определение машины Тьюринга.
Машина Тьюринга Т=<A, Q, > полностью определяется:
1) внешним алфавитом А=а
0
, а
1…
а
m
;
2) Алфавитом внутренних состояний Q=q
0
, q
1…
q
m
;
3) Программой , то есть совокупностью выражений Т(i, j) (i=0,n; j=0,m),
каждое из которых имеет вид следующей команды q
j
a
i
q
k
a
L
d
t
(k=0,n;
L=0,m; d
t
d
Л
, d
п
, d
н
.
a
0
a
4
a
1
a
0
a
0
a
0
a
4
a
2
a
0
a
0
52
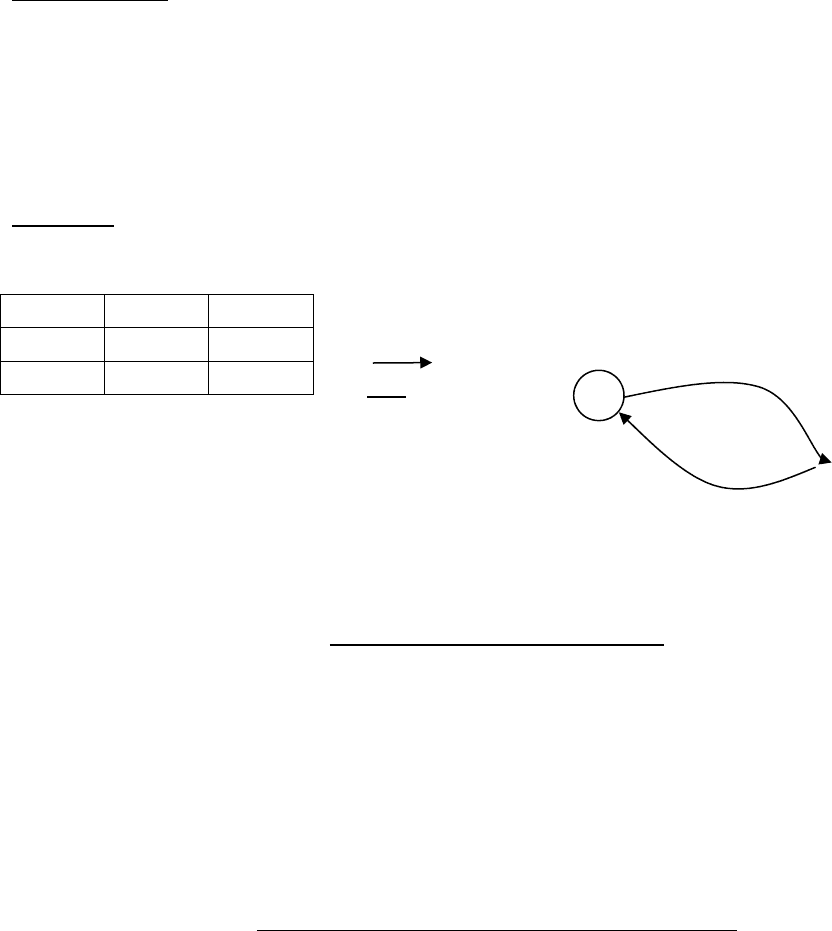
Машина Тьюринга есть формальная детерминированная система
F.S=<L, D>=<A, S; Ax, R>, порождающая множество L своих конфигураций
(машинных слов) 1 qj ai 2 (1, 2А*, 1 и 2 могут быть пустыми).
Единственная аксиома – начальная конфигурация q0 (А*), правила
вывода R – система команд (программа) Т(i, j).
Примечания:
1) Очевидно, что всякий алгоритм является формальной системой F.S,
что следует из тезиса Тьюринга: «Любой алгоритм может быть
реализован машиной Тьюринга».
2) Поскольку машина Тьюринга есть алгоритм, то записью последнего
является программа , а алгоритмом выполнения – описание
устройства машины Тьюринга.
Пример:
Построить машину Тьюринга для вычисления базисной рекурсивной
функции f(x)=x+1, xN
0
Имеем T=<A=a
0
, Q=q
0
, q
z
, =
>
Пусть:
а) х=0, тогда q
0
a
0
…a
0
q
z
d
н
;
б) х=2, тогда q
0
a
0
q
0
d
н
q
0
a
0
d
н
q
z
d
н
Основной тезис Тьюринга.
Утверждение: «Для любой вычислимой функции можно построить машину
Тьюринга, реализующую ее» - является гипотезой, называемой тезисом
Тьюринга. (Часто этот тезис формулируют так: «Всякая вычислимая функция
вычислима по Тьюрингу.)
Напомним, что этот тезис нельзя доказать, так как он объединяет два
понятия – расплывчатое, интуитивное понятие вычислимой функции и
строгое понятие машины Тьюринга.
Нормальные алгорифмы (алгоритмы).
Нормальные алгорифмы U=<A, > - класс словарных алгоритмов, то есть
алгоритмов (применимых к словам некоторого алфавита А), элементарными
действиями которых являются подстановки в слова (их кортеж есть схема ).
Всякий нормальный алгоритм, являясь алгоритмом в некотором алфавите
А, порождает в нем детерминированный процесс переработки слов. Поэтому
любой нормальный алгоритм в фиксированном алфавите А вполне
определяется указанием его схемы - упорядоченного конечного списка
формул подстановки в А. Каждая такая формула по существу представляет
пару <
Л
,
п
> слов в А (то есть
Л
,
п
А
*
). Слово
Л
называется левой частью
этой формулы, а
п
– ее правой частью. Среди формул данной схемы
A\Q q
0
q
z
a
0
d
н
q
z
a
0
d
н
q
z
d
н
q
0
d
н
q
z
53
или
d
п
d
п
а
0
d
н
q
0
q
z
некоторые выделяются специально и объявляются заключительными.
Обычно в схеме нормального алгоритма заключительная формула
записывается в виде
Л
п
(, а незаключительная в виде
Л
п
. При этом допустимы формулы вида :
Л
п
п
;
Л
Нормальный алгоритм U в алфавите А есть предписание строить, исходя из
произвольного слова в А (А
*
), последовательность слов
i
.
Так, пусть задан алфавит А=1, + и схема подстановок (здесь
- пустое слово, то есть А
*
, Слово этот алгоритм
перерабатывает так:
Процесс оканчивается применением заключительной подстановки, которая
перерабатывает слово само в себя. Очевидно, что рассматриваемый алгоритм
осуществляет операцию сложения (эквивалентный ему алгоритм
<А=1, +, ++, +, >).
Пусть теперь - некоторое слово в А, то есть А
*
. Говорят, что
поддается формуле, если левая часть этой формулы входит просто в .
Считается, что всякое слово начинается простым вхождением пустого слова
в . Считается, что всякое слово начинается вхождением пустого слова .
Поэтому всякое слово поддается формуле с пустой левой частью.
Применением нормального алгоритма U к слову
называется процесс,
определяемый следующим правилом (представляющая собой алгоритм
выполнения нормального алгоритма):
1) Считать, что i=1. Перейти к пункту 2.
2) Проверить, поддается ли преобразуемое слово i-ой формуле. Если да,
то перейти к пункту 3, если нет – к пункту 5.
3) Первое простое вхождение левой части i-ой формулы в преобразуемом
слове заменить правой частью i-ой формулы. Результат считать в
дальнейшем преобразуемым словом, перейти к пункту 4.
4) Если i-ой формула является заключительной подстановкой, то процесс
прекратить. В противном случае перейти к пункту 1.
5) Проверить, имеет ли место равенство i=n. Если да, то процесс
прекратить, в противном случае перейти к пункту 6.
6) Увеличить значение i на 1 и перейти к пункту 2.
Любое слово в алфавите А может служить исходными данными для
нормального алгоритма в алфавите А. При этом возможны случаи:
1) Процесс выполнения нормального алгоритма для слова А
*
заканчивается формулой
Л
п
после конечного числа шагов. При
этом говорят, что нормальный алгоритм применим к слову , и
полученное после его выполнение слово
*
называется
результатом.
54

2) Процесс выполнения нормального алгоритма при исходном слове
А
*
никогда не заканчивается или происходит безрезультативная
остановка (то есть не на формуле
Л
п
). В этом случае говорят,
что нормальный алгоритм не применим к слову .
Пример:
Алгоритм U=
«обращает» любое слово в А, то
есть перерабатывает его в слово, записанное в обратном порядке (его можно
записать как 100 с тем, чтобы использовать ).
Так, слово 100 этот нормальный алгоритм последовательно перерабатывает
в слова 010, 001, 001, 001, 001, 001, 001, 001,
001, 001, 001, 001, 001.
Замечание:
Последний член этой последовательности считается результатом применения
алгоритма U к слову =100 и обозначается символом U(). При этом
считается, что U перерабатывает =100 в =001, и пишут U()= (в нашем
примере U(100)=001).
Пример:
Алгоритм U=<a, b, <a b; baaba, aa> реализует предписание:
«Взяв какое-либо слово a, b
*
в качестве исходного, (где а, ba,
aa), делай допустимые переходы до тех пор, пока не получится слово
вида aa, тогда остановись: слово и есть результат».
Так, взяв слово babaa в качестве исходного данного после первого перехода
(то есть применив формулу ba aba ), получим baaaba (здесь =baa), а
после второго (то есть применив снова формулу ba aba) имеем aabaaba
(здесь =ааba. Применив формулу aa к слову aabaaba получим
результат baaba (то есть U(babaa)=baaba).
Однако, взяв в качестве исходного данного слова baaba, получим
бесконечную последовательность abaaba, baabab, abababa, bababab, babababa,
… в которой не будет слова aa. Это означает, что алгоритм U не будет
применим к слову baaba.
Если же исходным данным взять слово abaab, то получим конечную
последовательность baabb, abbaba, bbabab, в которой к последнему слову
нельзя применить допустимый переход, то есть это случай
безрезультативной остановки (это означает также применимость заданного
алгоритма U к слову abaab).
Считается, что для любого алгоритма В в алфавите А может быть построен
нормальнай алгоритм U над этим алфавитом, перерабатывающий
произвольное слово А
*
в тот же самый результат, в который
перерабатывает его исходный алгоритм В. Это соглашение известно в теории
алгоритмов под названием принципа нормализации.
Уточнение понятия алгоритма, осуществленного на основании понятия
нормального алгоритма, оказываетсяэквивалентным другим известным
уточнениям (в частности, на основе абстрактной машины Тьюринга).
Вследствие этого принцип нормализации оказывается равносильным тезису
55

Черча, предлагающему считать понятие частично рекурсивной функции
адекватным уточнением понятия вычислимой арифметической функции
f:N
n
0
N
0
, N
0
=N0, nN (к ней путем метода арифметизации могут быть
приведены числовые и нечисловые функции).
Рекурсивные функции.
Рекурсивная функция (частично рекурсивная функция) – функция, заданная
с помощью последовательности частичных (определенных не обязательно
для всех значений своих аргументов) функций таких, что каждая функция
последовательность либо является (базисной) простейшей функцией, либо
получена из предыдущих с помощью операторов суперпозиции
(подстановки) S
n
m
, примитивной рекурсии R
n
и минимизации .
Все рекурсивные функции являются вычислимыми функциями, то есть для
любой такой функции можно указать алгоритм вычисления ее значений.
Очевидно, что всякий алгоритм однозначно ставит в соответствие исходным
данным (в случае, если он определен на них) результат. Поэтому с каждым
алгоритмом однозначно связана функция, которую он вычисляет. Однако,
обратное, то есть: «для всякой функции существует вычисляющий ее
алгоритм», неверно.
Согласно тезису Черча, любая функция, считающаяся вычислимой в
интуитивном смысле, является рекурсивной функцией. Эта гипотеза (тезис)
подтверждается тем, что все известные вычислимые функции являются
рекурсивными. Тезис Черча позволяет придать интуитивному понятию
вычислимой функции алгоритмический смысл.
Понятие рекурсивной функции эквивалентно понятию функции,
вычислимой на машине Тьюринга.
В теории рекурсивных функций, рассматриваемой ниже, как и вообще в
теории алгоритмов, принят конструктивный, финитный подход, основной
чертой которого является то, что все множество исследуемых объектов (в
данном случае функций) строится из конечного числа исходных объектов –
базиса – с помощью простых операторов (операций), эффективная
выполнимость которых достаточно очевидна.
Замечание:
Всюду определенные рекурсивные функции называются общерекурсивными
функциями.
Примитивно-рекурсивные функции.
Def . Всюду определенная функция от натуральных аргументов с
натуральными значениями, которую можно получить из простейших
базисных всюду определимых функций
f(x)=x+1, z(x)=0, J
n
m
(x
1
,…, x
n
)=x
m
Конечным числом операторов (операций) суперпозиции (подстановок) S
n
m
, и
примитивной рекурсии R
n
называется примитивно-рекурсивной (ПРФ).
56

Базисную функцию f(x)=x+1 принято называть функцией следования (эту
функцию иногда обозначают х` и называют функцией прибавления
единицы), z(x)=0 – нуль функцией, J
n
m
(x
1
,…, x
n
)=x
m
– функцией тождества
(или введения фиктивных переменных), где nm.
Def . Оператором суперпозиции S
n
m
называется подстановка в функцию от m
переменных m функций от n переменных. (одних и тех же).
Говорят, что функция f(x
1
,…, x
n
) возникает из функций h(x
1
,…, x
m
), g
1
(x
1
,
…, x
n
), …g
m
(x
1
,…, x
n
) суперпозицией, если
f(x
1
,…, x
n
)= S
n
m
(h, g
1
,…, g
m
) = h(g
1
(x
1
,…, x
n
), …, g
m
(x
1
,…, x
n
)).
Если заданы функции J
n
m
и орераторы S
n
m
, то можно считать заданными
всевозможные операторы подстановки функции в функцию, а также
переименования, перестановки и отождествления переменных.
Так, если f(x
1
, x
2
)= h(g
1
(x
1
, x
2
), g
2
(x
1
, x
2
)), то ее стандартный вид следующий:
f(x
1
, x
2
)= S
2
2
(h(x
1
, x
2
), g
1
(x
1
, x
2
), S
1
2
(J
2
1
(x
1
, x
2
), g
2
(x
1
), g
3
(x
1
))), где g
3
– любая
функция от х
1
. Если же имеем f(x
2
, x
1
, х
3
, …, x
n
) и f(x
1
, x
1,
x
3
,…,
x
n
), то пишем:
f(x
2
, x
1
, х
3
, …, x
n
) = f(J
2
2
(x
1
, x
2
), J
2
1
(x
1
, x
2
), х
3
, …, x
n
),
f(x
1
, x
1,
x
3
,…, x
n
)= f(J
2
1
(x
1
, x
2
), J
2
1
(x
1
, x
2
), х
3
, …, x
n
).
Def . Оператором примитивной рекурсии R
n
называется процесс
определения функфии f (n+1) переменных через n-местную функцию g и
(n+2)- местную функцию h в следующем виде:
f(x
1
, x
2,
…, x
n
, 0)= g(x
1
, x
2
,…, x
n
)
f(x
1
, x
2,
…, x
n
, y+1)=h(x
1
, x
2
,…, x
n
, y, f(x
1
, x
2,
…, x
n
, y)),
где g и h – две различные функции соответственно n и n+2 аргументов.
Эта пара равенств называется схемой примитивной рекурсии. Тот факт, что
функция f определена схемой примитивной рекурсии выражается равенством
f(x
1
, x
2,
…, x
n
, y)=R
n
(g, h). В случае, когда n=0, то есть определяемая функция f
является одноместной, схема примитивной рекурсии принимает более
простой вид:
f(0)=с, f(у+1)=h(y, f(y)), где с – константа.
Схема примитивной рекурсии определяет f рекурсивно не только через
другие функции g и h, но и через значения f в предшествующих точках:
значение функции f в точке у+1 зависит от значения функции f в точке у.
Очевидно, что для вычисления f(x
1
,…, x
n
, k) понадобиться k+1 вычислений
по схеме примитивной рекурсии – для у=0, k.
Замечания:
1) Существенным в операторе примитивной рекурсии R
n
является то, что
независимо от числа переменных в f рекурсия ведется только по одной
переменной у (остальные n переменных x
1
, x
2,
…, x
n
на момент
применения схемы примитивной рекурсии зафиксированы и играют
роль параметров).
2) Формальное индуктивное определение примитивно-рекурсивной
функции следующее:
57

- функции 0, х`, J
n
m
для всех натуральных n, m, где nm являются
примитивно-рекурсивными;
- если g
1
(x
1
,…, x
n
), …g
m
(x
1
,…, x
n
), h(x
1
,…, x
m
) - примитивно-
рекурсивные функции, то S
n
m
(h, g
1
,…, g
m
) - примитивно-
рекурсивные функции для любых натуральных n, m;
- если g
1
(x
1
,…, x
n
) и h(x
1
,…, x
m
, у, z) - примитивно-рекурсивные
функции, то R
n
(g, h) – примитивно-рекурсивная функция;
- других примитивно-рекурсивных функций нет.
3) Схемной интерпретацией примитивной рекурсии может быть схема:
Эта схема состоит из элемента, вычисляющего за один такт функцию h
от двух переменных и элемента задержки на один такт. По каналам
схемы могут передаваться натуральные числа. Время t считается
дискретным, то есть t=0, 1, 2, 3…. Схема имеет один вход х и один
выход f. Выход f зависит не только от х, но и от момента t, в котором
он рассматривается. В начальный момент t=0 второй вход h является
константой с, зависящей от начального состояния схемы: f(x, 0)=h(x,
c)=g(x). В момент t=1: f(x, 1)=h(x, f(x, 0)); в общем случае f(x, t+1)=h(x,
f(x,t)). Нетрудно убедиться, например, что если h выполняет
умножение, а с=1, то f(x, t)=x
t+1
.
4) Поскольку исходные (базисные) функции являются вычислимыми, а
операторы суперпозиции и примитивной рекурсии вычислимость
сохраняют, то множество всех примитивно-рекурсивных функций есть
подкласс класса всех вычислимых функций;
5) Класс всех примитивно-рекурсивных функций счетен, поскольку
каждая такая функция задается описанием ее построения из исходных
функций.
6) Практически все арифметические функции, употребляемые в
математике по конкретным поводам, являются примитивно-
рекурсивными функциями, например: х+у, х*у, х
у
и т.д.
Оператор минимизации (
- орератор).
Def . Оператором минимизации
(оператором наименьшего числа)
называется преобразование (n+1)-местной функции (в общем случае
частичной) в n-местнуб f, такую, что для любых х
1
, х
2
, …х
n
, у равенство
58
h(x
1
, x
2
)
f(x, t)
x

f(х
1
, х
2
, …х
n
)=у имеет место лишь в том случае, если определены и не равны
нулю значения ( х
1
, …, х
n
, 0), …, ( х
1
, …, х
n
, у-1) и при этом
( х
1
, х
2
, …х
n
, у)=0. Применение оператора минимизации обозначают
[, (y)], где у - исчезающий аргумент.
Говорят, что n-местная арифметическая функция f: N
n
N получается из
функции : N
n+1
N с помощью -оператора, если выполнено условие: для
любых k
1
, k
2
,…, k
n
, kN.
f(k
1
, k
2
,…, k
n
)=k,
тогда и только тогда, когда для всех l<k значения ( k
1
, k
2
,…, k
n
, l)
определены и отличны от нуля, а значение ( k
1
, k
2
,…, k
n
, k) определено и
равно нулю.
Если f получается из функции с помощью оператора наименьшего числа
, то пишут:
f(x
1
, x
2
,…, x
n
)=y[(x
1
,…, x
n
, y)=0].
Важным свойством -оператора является то, что с его помощью из
вычислимой функции всегда получается частичная вычислимая функция f.
Именно, если имеется алгоритм для вычисления , то значение f(x
1
, x
2
,…, x
n
)
может вычисляться следующим образом:
- вычисляется (x
1
, x
2
,…, x
n
, 0);
- если процесс вычисления закончился, то есть значение
(x
1
, x
2
,…, x
n
, 0) определено, и (x
1
, x
2
,…, x
n
, 0)=0, то полагаем
f(x
1
, x
2
,…, x
n
)=0, а если (x
1
, x
2
,…, x
n
, 0)0, то начинают вычислять
(x
1
, x
2
,…, x
n
, 1). Если процесс вычисления закончился и
(x
1
, x
2
,…, x
n
, 1)=0, то полагают f(x
1
, x
2
,…, x
n
)=1, а если
(x
1
, x
2
,…, x
n
, 1)0, то переходят к вычислению (x
1
, x
2
,…, x
n
, 2) и так
далее.
- Процесс вычисления закончится, если найдется такое у, что для всех
z<y значение (x
1
, x
2
,…, x
n
, z) определено и отлично от нуля, а (x
1
,
x
2
,…, x
n
, у) определено и равно нулю. Тогда f(x
1
, x
2
,…, x
n
)=у.
Пример:
f(x)=y[12*y-x=0]. Тогда f(x)=x/2 при всех четных значениях хN.
Замечание:
Примитивно-рекурсивные функции всегда определены (имеют значения) для
любых значений аргументов. Иначе обстоит дело с функциями, полученными
при помощи -оператора. Для некоторых комбинаций значений аргументов
они могут быть не определены, потому что исходная функция не принимает
нулевых значений.
Пример:
det f(x)=[J
2
1
(x, y), (y)].
Полученная функция f(х) обладает следующими свойствами:
f(0)=0, f(k) не существует при k0. Последнее означает, что для заданной
функции J
2
1
(x, y) -оператор не может построить f(k) kN, так как при x=k
функция (x, y)= J
2
1
(x, y) ни для какого значения у не будет равной нулю.
59

Основной тезис Черча.
Утверждение:
«Какова бы ни была вычислимая неотрицательная функция от
неотрицательных целочисленных аргументов, существует тождественно
равная ей рекурсивная функция» - основной тезис Черча.
Перенеся тезис Черча на алгоритмы, сопутствующие рекурсивным
функциям, можно высказать и следующую гипотезу: «Каков бы ни был
алгоритм, перерабатывающий наборы целых неотрицательных чисел в целые
неотрицательные числа, существует алгоритм, сопутствующий рекурсивной
функции, который ему эквивалентен».
Приведенные гипотезы означают, что выполнение алгоритма в
определенном смысле эквивалентно вычислению значений рекурсивной
функции, а невозможность рекурсивной функции означает и невозможность
алгоритма (так как для каждого алгоритма должна быть рекурсивная
функция, а ее-то в данном случае и нет).
Напомним, что тезис Черча и следующие из него другие гипотезы не имеют
доказательства и принципиально не могут быть доказаны, так как в них речь
идет об алгоритмах в интуитивном смысле, не являющихся математическими
объектами.
Алгоритмически неразрешимые проблемы.
Массовые проблемы, для которых не существует эффективных методов
разрешения, называются алгоритмически неразрешимыми проблемами.
В интуитивном смысле массовая (алгоритмическая) проблема – это
бесконечный класс родственных единичных конкретных проблем,
правильный ответ для каждой из которых получается применением
алгоритма.
Фактически произвольную массовую проблему можно сформулировать как
проблему распознавания некоторого свойства Р элементов бесконечного
множества М; при этом единичные проблемы. составляющие массовую
проблему, связываются с элементами множества М, и каждая из них состоит
в том, что требует узнать, обладает или нет свойством Р соответствующий
элемент множества М. Поэтому задача ставится так: найти алгоритм,
применимый к любому элементу множества М и для каждого данного хМ
дает «1» или «0» в зависимости от того, обладает или нет элемент х
свойством Р. Массовая проблема называется неразрешимой, если такого
алгоритма нет.
Очевидно, принципиально неразрешимыми должны быть алгоритмы
получения объектов, которые парадоксальны, или решения проблем, из
которых вытекало бы (если бы они были разрешимы) существование
объектов.
Понятие алгоритмической неразрешимости уточняется с привлечением
математических понятий машины Тьюринга, рекурсивных функций,
нормальных алгоритмов и других.
60
