Маркин П.М. Математическая логика

Подождите немного. Документ загружается.

Б. Терм – языковое выражение для обозначения некоторых эмпирических и

абстрактных объектов. Термы строятся по определенным синтаксическим правилам

в конкретном языке логики. Обычно термы задают с помощью логических

переменных и терминов.

1. Логическая переменная – символ языка, обозначающий произвольный объект из

некоторого фиксированного множества объектов. В читаемом курсе логическими

переменными являются:

- предметная переменная – переменная, выражающая предмет(субъект,

индивидный объект);

Примеры:

1) Х – студент группы “C”, т.е. P

(

)

, где

Х – субъект ( на множестве студентов группы “C”; P - является студентом группы

“C”

2) Х+3=5 т.е. P

(

)

, где х – числовая переменная(т.е. место для подстановки цифр,

обозначающих конкретное число); P – является слагаемым уравнения 1-го порядка.

3) Х сын Y, P

(

x,y

)

, где x,y - прямые родственники, P - быть сыном.

- пропозициональная переменная – переменная, значениями которой

являются высказывания;

- лингвистическая переменная (в нечеткой логике) – переменная, значениями

которой являются субъективные словесные оценки;

- предикатная переменная - переменная, значениями которой являются

предикаты;

- метапеременная – переменная, вместо которой допускается подстановка

других переменных определенного вида.

2. Термин – символ имени (именной формы) конкретного объекта. Различают

термины:

- индивидные (предметные, субъектные) постоянные (константы);

- логические операторы (составляющие три подмножества – логические

связи, такие как, кванторы, такие, как ; символы

метавысказываний, а именно |=, |

- предикатные термины (двухместные отношения , ;

- истинностное значение – абстрактный объект, выступающий в качестве

характеристического свойства высказывания (в классической логике ={U,

}, а в неклассической - || >2; здесь  - множество истинностных

значений для высказываний).

- Метатермин – термин для обозначения множества терминов.

В. Логическая функция – функциональное соответствие на множестве кортежей

длины n>0, принимающее значение в множестве истинностных значений, т.е.

: M

 M

 …  M



Различают однородные (пропорциональные) и неоднородные (предикатные)

логические функции, т.е.

1) если M

= M

= … = M

= , то 

 - однородная логическая функция (в

частности, если || =2, то пишут f:{0,1}

{0,1}, или f: В

В и называют

функциями алгебры логики).

2) М

 - неоднородная логическая функция (в частности, М

{0,1} –

двузначный n-местный предикат)

3) Метафункция - метаформулы.

Г. Логическая формула – языковое представление суперпозиции логических

функций. В читаемом курсе будем различать формулы:

1) пропозициональную – правильно построенный кортеж из

пропозициональных переменных и логических связок;

2) предикатную – правильно построенный кортеж предикатов, логических

связок и кванторов;

3) метаформулу – кортеж метапеременных и логических операторов (т.е.

метаформула есть логическая форма формул).

Примечание.

- Как правило, определение логической формулы имеет индуктивный

характер:

 Выделяется класс языковых выражений, называемых простыми

(атомарными) формулами;

 Указываются правило, позволяющее из уже построенных

логических формул, строить новые логические формулы, используя

логические операторы.

- формула, подобно терму и переменной, есть семантический объект на

множестве языковых выражений и поэтому с синтаксической точки зрения

должна быть алгоритмически разрешимой.

ПОСТРОЕНИЕ МАТЕМАТИЧЕСКОЙ ЛОГИКИ.

Математическая логика является теорией (т.е. целостной системой абстрактных

объектов, отражающей основные закономерности логического мышления) в том

плане, что ее основными структурными компонентами являются:

1) концептуальный базис (т.е. исходные понятия и основные отношения

между этими понятиями, выраженные в форме аксиом, законов,

гипотез).

2) Дедуктивные средства (т.е. отношение логического следования,

выраженное в форме тех или иных правил логического вывода).

3) Содержательная надстройка (т.е. совокупность суждений, выраженных в

форме конкрентных высказываний и теорем, полученных из

концептуального базиса с помощью дедуктивных средств).

В том случае, когда абстрактные объекты теории отображаются с помощью

формального или формализованного языка L=<A,S> (соответственно, L

=<A,S> ,

=<A, S

, S

> , где А – алфавит символов, S

– синтаксические правила построения

языковых выражений FA

, S

- семантические правила ) и явным образом

определены постулаты D (т.е. аксиомы A

 F A

и дедуктивные средства P  F

n+1

то говорят о построении теории как формальной системы F.S. = <L, D> = <A, S, A

P> <A, F, A

, P>. Примером так построенной теории в читаемом курсе будут

рассмотрены исчисления высказываний и предикатов (это т.н. логические

исчисления).

Другим подходом к построению математической логике является - содержательный,

т.е. неформальный. В этом случае аксиомы и дедуктивные средства явным образом

не определяются (т.е. постулаты в таком построении теории используются

интуитивно). Примером содержательно построенной математической логикой

является алгебра логики – алгебра высказываний А

=<{U, }, , , > и алгебра

предикатов А

=< F, , {U, }

{U, },  > (где F – множество предикатных

формул,  - символ отрицания, {U, }

{U, } – бинарные логические связки, -

квантор всеобщности,  - квантор существования).

Замечания.

1) Содержательная надстройка современных теорий строится на основе

точно заданного концептуального базиса нечетко определенных

дедуктивных средств.

2) Необходимым, но недостаточным условием научной состоятельности

теории является ее внутренняя непротиворечивость.

3) Логические исчисления являются важнейшей разновидностью

формальных систем F.S. От других формальных систем ( например,

интегрального и дифференциального исчисления) логические

исчисления отличаются чисто логическим пониманием правильно

построенных языковых выражений FA

и правил вывода P : (F

, F

,…, F

n+1

)  F

n+1

4) На основе логических исчислений строятся ( путем присоединения

некоторых дополнительных аксиом) прикладные исчисления.

5) Для всякого логического исчисления важное значение имеет вопрос о

его непротиворечивости, независимости, полноте, разрешимости.

6) Говорят, что всякая интерпретированная формальная система (т.е. когда

L=<A, S

, S

> ) представляет собой формализованный язык, в котором

заданы S

- правила синтаксиса и S

- правила семантики

(интерпретации). Именно в этом плане изучаемые в курсе исчисления

высказываний 

и предикатов 

являются интерпретированными

логическими формальными системами (или логическими языками).

Примером интерпретированных прикладных логико-математических

F.S. (или т.н. логико-математических языков) являются различные

аксиоматико-дедуктивные теории множеств.

7) F.S. есть порождающая процедура (т.е. аксиоматико-дедуктивный способ

индуктивного порождения элементов множества из исходных объектов,

рассматриваемых как аксиомы, или разрешаемое подмножество A

 F),

а интерпретация, как метод, является распознающей процедурой (т.е.

способом распознавания принадлежности объекта заданному

множеству).

8) Правила вывода P формальной системы < L, D > есть конечное

множество вычисляемых (разрешающих) отношений на множестве

языковых выражений FA

Для лучшего усвоения формального построения теории приведем примеры

формальных систем F.S., несвязанных с логическими интерпретациями.

Пример 1 . Пусть F.S.= <A, S, A

, P> есть описание (интерпретация) игры в шахматы,

т.е. F.S. описывает множество допустимых шахматных позиций. В этом случае

алфавит А состоит из 64 клеток доски, занятые фигурами и свободные;

синтаксические правила S порождают множество допустимых позиций F; аксиомой

(единственной) A

является исходная шахматная позиция; правилами P являются

правила, определяющие следующие ходы (чередование ходов белых и черных

фигур, правила взятия фигур, рокировки, допустимого хода фигур на свободные

клетки) и заключительные позиции – ничейные, матовые.

Пример 2. Фраза русского языка описывается F.S., алфавит которой А – алфавит

русского языка, S – грамматические правила построения слов русского языка F,

аксиомы A

x –

слова фразы, а правила вывода P , т.е. правила построения фразы из

слов – правила синтеза фраз в грамматике русского языка.

Пример 3. Формальная грамматика есть формальная система, описывающая

синтаксис искусственного языка. В этом случае алфавит А есть объединение двух

непересекающих подмножеств символов терминального Т и вспомогательного V

словарей (т.е. А=ТV), а формулами – цепочки из этих символов (т.е. FТV

Единственная аксиома  в этой формальной системе является элементом

вспомогательного словаря V (т.е. V), правило вывода позволяет получать

цепочки в терминальном алфавите ( эти цепочки являются словами искусственного

языка – множества, порождаемого формальной грамматикой) и имеют вид h, где

, hТV

. Так, формальная грамматика (система) 

порождает (описывает) множество (язык) нечетных чисел в унарном представлении,

т.е. множество цепочек вида , ,…, 

2n-1

,… (здесь nN ).

Пример 4. Индуктивное определение можно представить формальной системой,

аксиомы которой перечислены в базисе (первом пункте) определения, а правила

вывода – в индуктивном (втором пункте) шаге. Необходимым условием перехода к

формальной системе в этом случае является разрешимость множества аксиом.

Так, индуктивное определение двухполюсной системы вида

с d

Может быть следующим:

1) объект ха, б, с, д,…, к является схемой, полюсы которой совпадают

с полюсами объекта (язык построения объекта L( может быть описано,

например, какой-нибудь формальной грамматикой)

2) если С

и С

– схемы, то

также схемы (это т.н. правила последовательного p

и параллельного p

соединения схем в схему)

3) других схем нет.

В этом случае F.S.= < L (),а, б, с, д,…, к, p

, p

 >

ЯЗЫК КЛАССИЧЕСКОЙ ЛОГИКИ ВЫСКАЗЫВАНИЙ L

= < A

, F

А. Синтаксис языка Л.В,

Перечисленные множества исходных символов алфавита A

и правил образования

языковых выражений, составляет синтаксис языка логики высказываний (Я.Л.В.).

I. Алфавит Я.Л.В.

В =





; 



= , ij; 

={p, q, x, y,…,p

, q

, x

, y

,… p

, q

, x

, y

,… } –

множество дескриптивных (нелогических) символов, называемых

пропозициональными термами (переменными). Эти символы используются как

параметры (буквы) простых высказываний (при выявлении логических форм

контекстов естественного языка). 

={} – множество логических символов

(констант), называемых пропозициональными связками. Эти символы являются

терминами, обозначающими логические отношения и образующие

функционально-полную систему (т.е. из них можно выразить любую

логическую функцию).



={(,) } - множество разделительных (технических) знаков

Примечание.

1) 



– есть множество значащих символов.

2) В языке логики высказываний логические связки получают единую и

постоянную интерпретацию ( - не;  - или;  - и;  - если…то), а

пропозициональные переменные в составе формул и формулы могут

получать различные интерпретации от случая к случаю. Существование

такой интерпретации определяет семантику языка.

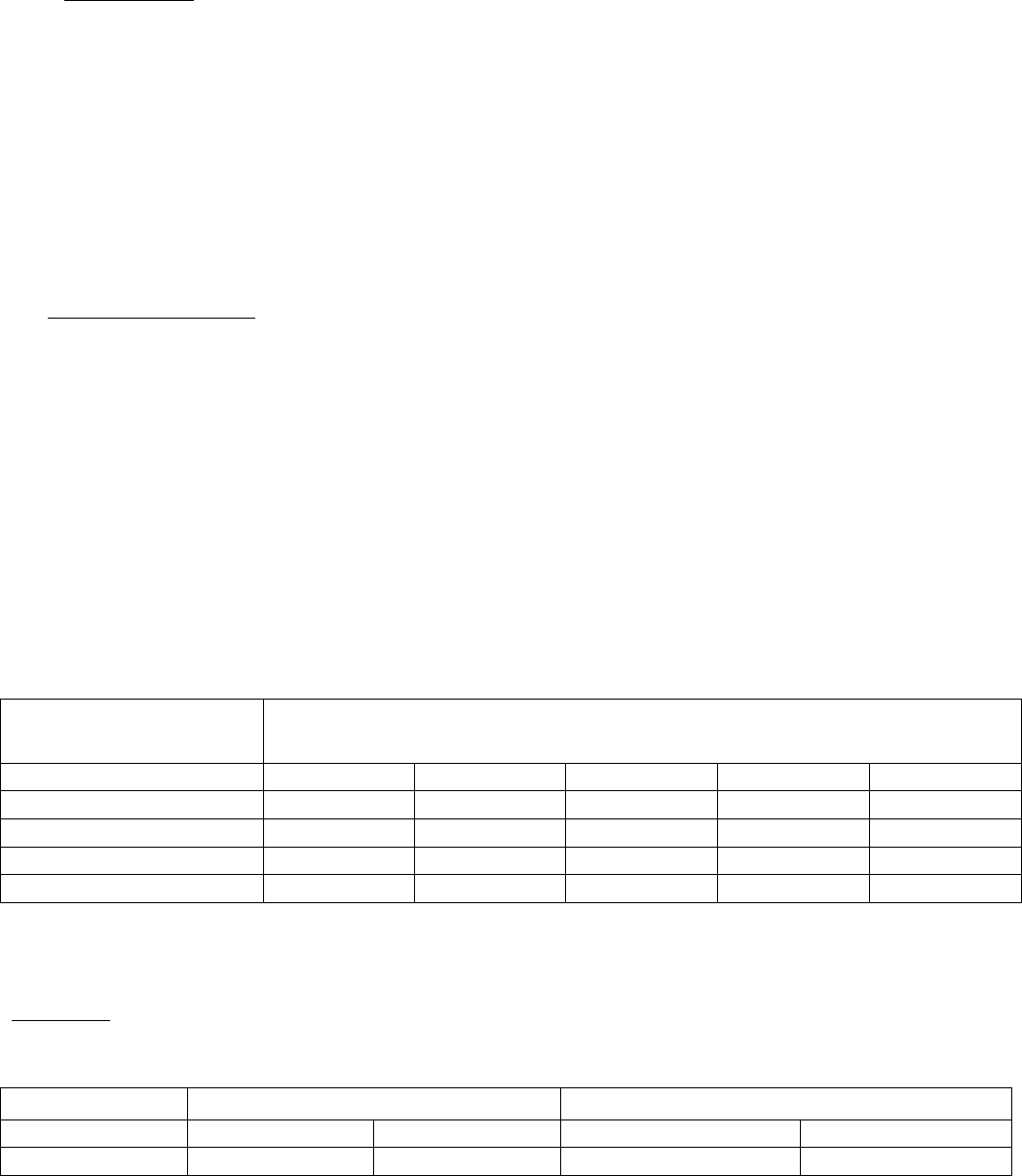
II. Языковые выражения Л.В.

Языковыми выражениями в логике высказываний являются формулы,

называемые пропозициональными формулами. Язык формул с переменными

x,y,z порождается формальной грамматикой = <Т, V, , P >, где Т= x,y,z, 

; V ={}, P =хy,

z

Замечание.

1) В алгебре логике формулы Я.Л.В. являются аналитическим способом

представления (реализации, задания) пропозициональной функции {U,

}

{U, }, а в логике высказываний – логическими формами

высказываний.

2) Принять следующие сложные высказывания (задаваемые их логическими

формами, т.е. формулами Я.Л.В.) (ху), (ху), х  у, х называть

соответственно дизъюнктивным, конъюнктивным, импликативным и

отрицанием, связки   - дизъюнкцией, конъюнкцией, импликацией,

отрицанием.

Б. Семантика Я.Л.В.

Интерпретации подлежат пропозициональные переменные и пропозициональные

формулы. Поскольку логические связки имеют постоянную интерпретацию, то

формулы, приобретя тем самым некоторый смысл, представляют собой логические

формы сложных высказываний. В таком смысле пропозициональные формулы

называют полуинтерпретированными. Полная интерпретация формулы получается в

результате приписывания истинностных значений пропозициональным переменным.

В этом случае полностью интерпретированная формула есть некоторое

высказывание Я.Л.В. Поскольку каждой формуле Я.Л.В. можно поставить в

соответствие таблицу истинности, указывающей зависимость истинностного

значения формулы от истинностных значений ее переменных, то имеем для

логических связок их табличное представление.

Пропозициональные

переменные

Пропозициональные формулы

x y х (ху) (ху) х  у

 



U U U



 

U U



U U U

Использование таких таблиц позволяет вычислить истинностное значение любой

формулы Я.Л.В.

Пример . Вычислить истинностное значение высказывания вида:

((ху) х), если х=, у= U. Имеем

Переменные Подформулы Формулы

х у (ху) х (ху) х



U U U U

Т.е. при заданной интерпретации простых высказываний сложное высказывание

истинно. Часто результат интерпретации формулы записывают так:

|((ху) х)| = И при х=, у= U.

Примечание. Для упрощения записи логических форм

1) вводят старшинство связок, а “лишние” скобки опускают;

2) используют производные связки (связки  в таком случае

называют основными).

Пояснения:

1) о соглашениях по сокращению записи формул над множеством логических

связок:

- внешние скобки формул опускаются

- формуле х записывается в виде х ;

- формуле (ху) записывается в виде ху ( т.е. скобки и символ операции

опускаются);

- приоритет в последовательности применения связок возрастает в

следующем порядке:  ( т.е. унарная связка  сильнее любой

бинарной операции; связка  - самая сильная бинарная операция).

Эти соглашения позволяют записать формулу:

_ _

((((х) у)  z) ( х (y)  z)) записать в более компактном виде ( ху)zxyz

2) Производные связки для сокращения записи логических выражений

- оператор “эквиваленция”  (интерпретируется как союз естественного

языка “тогда и только тогда”) позволяет формулу (ху)  (ух) записать в

виде ху, т.е. (ху)(ух)= ху (часто  называют оператором

эквивалентности)

- строгая дизъюнкция   (интерпретируется как союз “либо…либо” )

позволяет формулу (х y)  (х  у) записать в виде х  у (часто вместо

символа  используется символ , т.е. пишут ху);

Введенные связки позволяют легко выявить логическую форму высказывания

“треугольник не является прямоугольным тогда и только тогда, если верно одно из

двух: он либо остроугольный, либо он тупоугольный”. Пусть для этого

высказывания пропозициональными переменными будут х, у, z, т.е.:

х – треугольник прямоугольный,y - треугольник остроугольный, z - треугольник

тупоугольный. Терминам “не” соответствует связка , “тогда и только тогда” - ,

“либо…либо” - . Логическая форма исходного высказывания х  (у z), в Я.Л.В.

имеет вид:

_ _ _ _ _ _ _ _

(х  (у z))( (у z) х) = (хyz  yz)(yz  yzx)

Замечание . Высказывание, построенное из других высказываний с помощью

оператора эквивалентности, называют тавтологией.

Пример. Сложное высказывание “Земля по форме есть эллипсоид Красовского тогда

и только тогда, если неверно, что Земля не есть по форме эллипсоид Красовского”.

Это высказывание (его логическая форма   ) есть тавтология 



, где 

–

первое простое высказывание, а 

– второе простое высказывание исходного

сложного высказывания.

КЛАССИЧЕСКАЯ ЛОГИКА ВЫСКАЗЫВАНИЙ

Содержательно пропозициональную логику определяют как раздел математической

логики, формализующей употребление логических связок, служащих для

образования сложных высказываний из простых. Как и любая другая логическая

теория, логика высказываний решает две задачи:

- выделяет среди класса формул множество своих законов;

- устанавливает логические отношения между формулами.

В этом плане формально логику высказываний понимают как определенное на

множестве формул языка логики высказываний отношение логического следования |

= и законов, т.е. < F,|= >, с привлечением таблиц истинности.

а) Законы классической логики высказываний.

Определение. Формула, которая при любых распределениях истинностных значений

ее параметров принимает значение “истина”, называется общезначимой.

Определение. Денотат (т.е. объект обозначения) метевысказывания об

общезначимости пропозициональной формулы называется логическим законом.

Для метавысказывания “А есть логический закон” принять обозначение |=A (здесь А

– метаформула). Так, принцип исключенного третьего выражается

метавысказыванием |= ( , говорящим о том, что общезначимой является

пропозициональная формула ( , а принцип противоречивости выражает

метавысказывание |=(  , говорящее о том, что общезначимой является формула

(  , (где  - пропозициональная переменная, |= - оператор логического

следования). При подстановке вместо  любых конкретных высказываний (как

истинных, так и ложных) из формул (  и  (  получаются только истинные

высказывания.

Замечание.

1) Факт общезначимости пропозициональной формулы устанавливается с

привлечением таблицы истинности (пассивный метод) или

эквивалентным преобразованием (активный метод).

2) Каждый закон логики имеет бесконечное множество вариантов

формульного представления. Так принцип исключенного третьего может

быть записан следующими аналитическими выражениями:

|=x x; |=(ху) (ху); |=((xz) (yp)  ((хz)(yp));

3) Тождественно-ложная формула (т.е. формула, имеющая значение “ложь”

на всех значениях истинности ее переменных) являются отрицанием

закона логики.

б) Отношения логического следования и логической эквивалентности.

I. Из множества формул T логики следует формула В (символическая

запись T |=B, или R(F

, F

,…, F

, F

n+1

=B), где T ={ F

,…, F

}) в логической

теории, если и только если в теории не существует интерпретации нелогических

символов, входящих в T и В, при которой каждая формула из T принимает

значения “истина”, а формула В - значение “ложь”. Иначе, логическое следование





- отношение между пропозициональными формулами 

и 

такое, что





. В противном случае, т.е. когда формулы T истинны, а В – ложны, то В не

следует из T (символически запись T |В). В логике высказываний эффективной

процедурой (алгоритмом) выявления отношения логического следования между

конечным множеством формул T и формулой В является таблица истинности.

Пример 1. Проверить правильность умозаключения “Если тело движеися

равномерно и прямолинейно, то на него не действуют силы. Тело движется

равномерно, но не прямолинейно. Следовательно, на тело действуют силы”.

Логическая форма заданного умозаключения имеет вид:

((рq) z)

(р  q )

здесь р – “тело движется равномерно”

q – “тело движется прямолинейно”

z – “на тело действуют силы”

Таблица истинности умозаключения имеет вид:

Пропозициональные

переменные

посылки заключение

p q z ((рq) z) (рq) z



В четвертой строке этой таблицы посылки истинны, а заключение – ложно.

Поэтому из ((рq) z), (рq) не следует логически z и, следовательно,

умозаключение является неправильным.

Напоминание . Следует различать правильность умозаключения и истинность

заключения. В общем случае ложное заключение может быть получено в

результате следующих умозаключениях:

- все посылки T истинны, а само умозаключение не правильно;

- умозаключение правильно, но в нем есть ложная (ложные) посылки;

- умозаключение не правильно и в нем есть ложная посылка. В этом плане

следует отметить, что если к истинным посылкам T применяется

правильное умозаключение, то с логической неотвратимостью будет

получено истинное заключение В, т.е. T |=В.

Пример 2. Согласно легенде обоснования сожжения книг Александрийской

библиотеки :

- если ваши книги согласны с Кораном (р), то они излишни (q), (рq)

- если же ваши книги не согласны с Кораном (р), то они вредны (z), (рz)

посылки T

заключение

- но вредные (z) или излишние(q) книги следует уничтожать(у), (qz) y

Поэтому ваши книги следует уничтожать.

Покажем, что это рассуждение правильно, но заключение ложно. Действительно,

логическая форма рассуждения имеет вид:

рq

рz

(q  z)  y

Построив таблицу истинности, заключаем, что (рq), (рz), ((qz) y) |= y.

Аналитически этот результат можно получить, если учесть, что согласно теореме

дедукции:

|=( F

…( F

В)…)  F

,…, F

|=В, в нашем случае: надо показать, что

|=(( рq) ((рz) (((qz) y))), т.е. ((рq) ((рz) (((qz) y) y)))=

...)

(

)

(

)

(

)()()

()())(())))(((

(

____

____________

________

__________

____

_________

дтчuyz

qqz

yzq

yzp

pyy

zpq





























Пример . Рассуждение “Если на данное движущееся тело не действуют никакие

силы или равнодействующая всех действующих сил равна нулю, то оно движется

равномерно. Данное тело движется неравномерно, следовательно,

равнодействующая всех действующих сил не равна нулю”. Это умозаключение,

логическая форма которого

((рq) r)

r 

q

правильно, т.е. ((рq) z), r |=q

действительно:

_ _ _ _ _ _ _ _ _ _ _ _ _ _

(((рq) r) (rq))  (p qr) (rq)  (p r  q r  r  q)  (p r  q r  r  q rq r )  (p r  r 

 r )=u

II. Формулы А и С логически эквивалентны (логически равнозначны), если и

только если из А логически следует С и из С логически следует А, т.е. имеет место

двустороннее логическое следование:

A|=C и C|=A

Из этого определения вытекает, что в каждой строке совместной таблицы

истинности обе логически эквивалентные формулы принимают одинаковые

значения, что можно записать следующим образом АС(АС)(СА). Если

АС и СА тождественно истинны, то АС есть закон, т.е. |= АС.

посылки

заключение