Мангейм Дж.Б., Рич Р.К. Политология. Методы исследования
Подождите немного. Документ загружается.

Из этого следует, что
a = – b
Поскольку теперь мы знаем все нужные значения, мы можем определить, что
[c.431]
а = 12,88–(–0,12)(37,08)= 12,88+4,45= 17,33.
Таким образом, уравнение регрессии, наилучшим образом подытоживающее
распределение линии для данных, представленных на рис. 18.3, будет
выглядеть так:
Y’ = 17,33–0,12Х.
Используя это уравнение, мы можем вычислить значение Y для любого
конкретного значения.
Поскольку это уравнение решено, мы можем использовать коэффициент
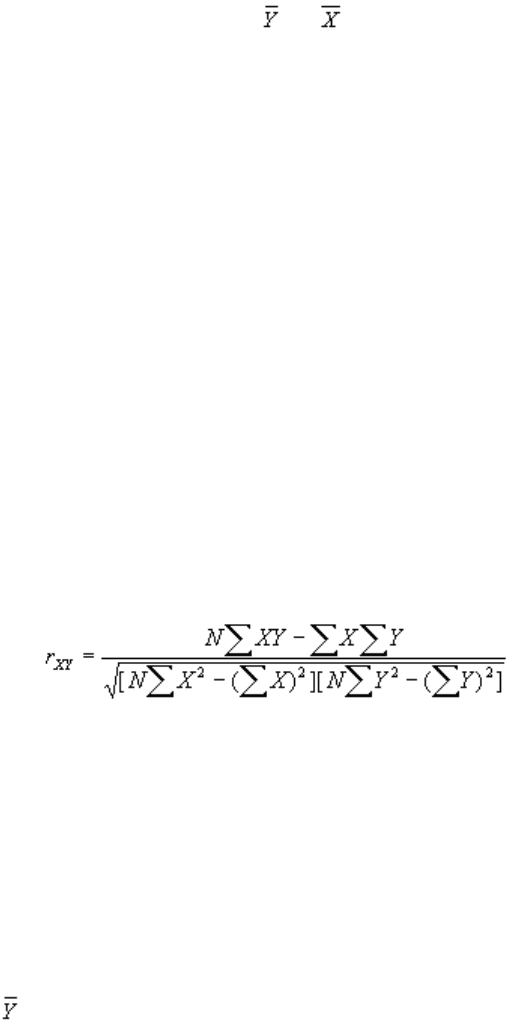
корреляции (r) для оценки репрезентативности линии регрессии. Формула r
XY
(коэффициента корреляции между X и Y) такова:
,
где Х – каждое значение независимой переменной (знак i применялся ранее для
большей наглядности);
Y – каждое значение зависимой переменной;
N – количество признаков.
Хотя это утверждение, безусловно, не так уж очевидно, а его алгебраическое
доказательство лежит за рамками нашей книги, эта рабочая формула получена
из сравнения первичной ошибки в предполагаемых значениях Y с
использованием среднего геометрического частотного распределения с
реальной ошибкой, получившейся в результате определения значений Y с
использованием Y' (уравнения линии регрессии). Таким образом, процедура
подсчета r аналогична той, которая использовалась для подсчета как l, так и G.
Наилучшим образом ее дополнит построение таблицы такого типа, с которой
мы уже знакомы; в ее колонках расположены значения X, Y, XY, X
2
и Y
2
. Суммы,
которые и нужны в уравнении, расположены в графе итого. Так, для данных,
представленных на рис. 15.3, для которых мы уже определили линию
регрессии, такой схемой будет табл. 15.7. [c.432]
Таблица 15.7

Значения, используемые при определении коэффициента корреляции (r)
х у ху х
2
у
2
30
30
30
30
30
31
31
31
33
33
35
35
35
36
36
37
40
40
40
42
42
50
50
50
50
Итого 927
10
11
12
14
16
14
15
16
15
16
12
13
15
12
13
13
10
12
14
10
12
9
10
12
16
322
300
330
360
420
480
434
465
496
495
528
420
455
525
432
468
481
400
480
360
420
504
450
500
600
800
11803
900
900
900
900
900
961
961
961
1089
1089
1225
1225
1225
1296
1296
1369
1600
1600
1600
1764
1764
2500
2500
2500
2500
35525
100
121
144
196
256
196
225
256
225
256
144
169
225
144
169
169
100
144
196
100
144
81
100
144
256
4260
Мы подставляем итоговые значения в уравнение:
Это говорит нам о том, что наклон у линии регрессии отрицательный (что мы
уже, собственно, знали) и что точки [c.433] группируются вокруг нее в ступени
от слабой до умеренной (поскольку г изменяется в пределах от +1 до –1 с
минимальной связью при r=0).
К сожалению, сам коэффициент r интерпретировать нелегко. Можно, однако,
интерпретировать r
2
как степень уменьшения ошибки в определении Y на
основании значений X, т. е. доля значений Y, которые определяются (или могут
быть объяснены) на основе Х. r
2
обычно представляют как процентную долю
объясненных значений, тогда как (1– r
2
) – долю необьясненных значений. Так, в
нашем примере r значением –0,38 означает, что для тех случаев, которые мы
анализируем, разброс независимой переменной составляет (–0,38)
2
, или около
14%, значений зависимой переменной год обучения.
По причинам, которые находятся за рамками настоящего разговора, определить
статистическую значимость г можно только в том случае, если обе – и
зависимая и независимая – переменные нормально распределены. Это можно
сделать, используя табл. А.5 в Приложении А, для чего нужны следующие
сведения. Во-первых, сам коэффициент г, который, конечно, известен. Во-
вторых, аналогично подсчету χ
2
количество степеней свободы линии регрессии.
Поскольку прямую определяют любые две точки (в нашем случае пресечение
и – первая точка, и пересечение с осью Y – вторая), все другие точки,
обозначающие данные, могут располагаться произвольно, так что df всегда
будет равно (N–2), где N – количество случаев или признаков. Таким образом,
для того чтобы воспользоваться таблицей, нужно определить примерное
количество степеней свободы (в нашем примере N–2 = 25–2 = 23) и
желательный уровень значимости (например, 0,05) так же, как мы делали для
нахождения χ
2
, определить пороговое значение r, необходимое для достижения
данного уровня значимости, и все подсчитать. (В нашем примере это значит,
что мы интерполируем значения в таблице между df=20 и df=25. Для df=23 это
будут следующие значения: 0,3379; 0,3976; 0,5069; 0,6194 соответственно.)
Таким образом, r=–0,38 статистически значим на уровне 0,10 (он превышает
0,3379), но не на уровне 0,05 (он не превышает 0,3976). Интерпретация этого
результата та же, что и в других случаях измерения статистической значимости.
[c.436]
ЗАКЛЮЧЕНИЕ
В этой главе мы познакомили вас с наиболее распространенными
статистическими процедурами, которые используются при изучении
взаимосвязей между двумя переменными. Как и в гл. 14, мы выяснили, что для
разных уровней измерения анализируемых данных подходят разные способы
вычисления связи и статистической значимости. Вместе с методами,
представленными ранее, рассмотренные коэффициенты снабдят исследователя
некоторыми очень полезными основополагающими способами получения
научных результатов. В следующей главе мы обратимся к более сложным
статистическим методикам, которые обогатят наши возможности анализа и
понимание того, что мы изучаем. [c.437]
Дополнительная литература

Библиографию по статистике см. к гл. 16.
Далее:
16. СТАТИСТИКА III: ИЗУЧЕНИЕ ВЗАИМОСВЯЗЕЙ МЕЖДУ
НЕСКОЛЬКИМИ ПЕРЕМЕННЫМИ
К оглавлению
ПРИМЕЧАНИЯ
1
Об определении этого понятия см.: Freeman L.C. Elementary Applied Statistics:
For Students in Behavioral Science – N.Y.: Wiley, 1965.
Вернуться к тексту
2
Полное объяснение статистической значимости требует гораздо более
пространного изложения, чем мы можем позволить себе здесь. Читателю
можем посоветовать обратиться к одному из изданий по статистике,
перечисленных в списке дополнительной литературы к гл. 16. Наш разговор, по
сути дела, будет ограничен тем, что такое ошибка первого порядка, не
принимая во внимание так называемую нулевую гипотезу (гипотезу,
предполагающую, что между двумя переменными не существует никакой
связи).
Вернуться к тексту
3
Собственно, коэффициент, который мы здесь описываем, – это λ или λ
a
(ассиметричная), измерение, которое проверяет наличие связи только в одном
направлении (от независимой переменной к зависимой). Тест на проверку
истинной λ связи тоже возможен (см.: Freeman, p. 71–76).
Вернуться к тексту
4
В таких условиях λ может быть ненадежна, но мы включили этот сюжет для
того, чтобы облегчить понимание концепции связи в целом. Соответствующий
коэффициент – коэффициент Кендалла – может быть более надежен, но его
определение более сложная процедура для начинающих статистиков.
Вернуться к тексту
5
Из всего этого, таким образом, следует, что единственный тип связи, который
измеряется коэффициентом r, – это линейная (прямолинейная) связь.
Существуют и другие статистические приемы, позволяющие измерить более
сложные типы взаимосвязей (например, криволинейную связь); можно также
преобразовать интервальные данные в порядковые категории и прийти, таким
образом, к более простым типам взаимосвязей.
Вернуться к тексту

Мангейм Дж.Б., Рич Р.К. Политология. Методы исследования: Пер. с англ. /
Предисловие А.К. Соколова. – М.: Издательство “Весь Мир”, 1997. – 544 с.
Красным шрифтом в квадратных скобках обозначается конец текста на
соответствующей странице печатного оригинала данного издания
16. СТАТИСТИКА III: ИЗУЧЕНИЕ ВЗАИМОСВЯЗЕЙ МЕЖДУ
НЕСКОЛЬКИМИ ПЕРЕМЕННЫМИ
Одномерный и двумерный статистический анализ, описанный в предыдущих
главах, часто бывают совершенно необходим для понимания объекта, который
мы изучаем. Однако одномерный и двумерный анализ почти никогда не
обеспечивает убедительной проверки гипотез или теорий, из которых они были
извлечены. Для того чтобы проверить какую-либо гипотезу, необходимо
исключить главную альтернативную конкурирующую гипотезу. И хотя четко
поставленные исследовательские задачи иногда позволяют нам не принимать
во внимание альтернативную гипотезу, обычно предпочитают проверять
справедливость конкурирующей гипотезы, опираясь на анализ данных, а не на
постановку задач исследования. А это требует многомерного анализа, т.е.
одновременного анализа взаимосвязей между тремя и более переменными.
[c.438]
АНАЛИЗ ТАБЛИЦ
Многие из статистических методов, уже описанных нами, могут применяться в
многомерном анализе
1
.
Для иллюстрации мы можем использовать очень упрощенный пример и
предложить метод, которым таблицы корреляции и бипараметрическая
статистика могут быть адаптированы для проведения многомерного
статистического анализа. Предположим, что мы хотим исследовать, какая связь
существует между политическим мировоззрением и получением образования в
колледже. Мы можем , предположить, что обучение в колледже дает людям
некую опору для поддержания статус-кво и подготавливает их к относительно
хорошему функционированию в рамках существующей социоэкономической
системы. Тогда возможно мы начнем с гипотезы, что те, кто окончил колледж,
будут более консервативны, чем те, кто не имел такой возможности. Чтобы
проверить эту гипотезу, нам надо протестировать выборку из 50 респондентов,
окончивших колледж и еще 50 таковых, в колледже не учившихся. [c.438]
Таблица 16.1.
Соотношение между получением образования в колледже и
политическим мировоззрением

Образование
в колледже
Мировоззрение
Либералы (%) Консерваторы
(%)
Общее число
респондентов
Получили
Не получили
Всего:
40……………(20)
60……………(30)
100……………(50)
60……………(30)
40……………(20)
100……………(50)
(50)
(50)
(100)
Наши гипотетические результаты представлены в табл. 16.1. Диагональное
“распределение” случаев в этой таблице показывает, что можно более или
менее характеризовать как консерваторов прежде всего тех, кто учился в
колледже. Подсчитав критерий “хи-квадрат” для этой таблицы, мы выясним,
что отношения между посещением колледжа и политическим мировоззрением
статистически значимы на уровне 0,01. Все это совпадает с нашей
первоначальной гипотезой.
Тем не менее, прежде чем мы рискнем представлять полученные данные в
American Political Science Review, нам необходимо проверить некоторые
альтернативные конкурирующие гипотезы, чтобы удостовериться, что наши
результаты обоснованны. Сделать это можно несколькими способами. Один из
них – это расширить наш бипараметрический анализ до многомерного анализа,
который позволит нам “проконтролировать” влияние других переменных на
отношение между получением образования в колледже и мировоззрением.
Например, одна альтернативная конкурирующая гипотеза, достойная изучения,
вытекает из наблюдения, что мужчины обычно более консервативны, чем
женщины. Если в нашей выборке больше мужчин, чем женщин, то результат,
представленный в табл. 16.1 может отражать различия мнений по половому
признаку, а не действительное влияние образования на политические мнения.
Чтобы исследовать эту возможность, мы можем проверить отношения между
образованием и воззрениями отдельно для мужчин и женщин. Тогда мы
построим две табл. сопряженности – 16.2 и 16.3. Если альтернативная
конкурирующая гипотеза обоснованна, то статистические отношения между
этими признаками, показанные в [c.439] табл. 16.1, не будут показаны в новых
таблицах, так как влияние “мужского” или “женского” начала будет исключено.
Такой процесс поддержки постоянного влияния третьей переменной на
отношения между двумя другими переменными отсылает нас к процедуре
контролирования и является важным шагом во всех формах многомерного
анализа.

В нашем случае табл. 16.2 и 16.3 на самом деле показывают, что отношения
между получением образования в колледже и мировоззрением по существу
одинаковы и для мужчин и для женщин. Хотя женщины в нашей выборке, как и
было предсказано, не так консервативны, как мужчины, “распределение” в этих
двух таблицах практически одинаково, и вычисление “хи-квадрат” критерия
для каждой из них показывает, что те отношения, которые они представляют,
статистически значимы. В такой ситуации исследователи говорят, что
первоначально предположенные отношения “проконтролированы” и что
альтернативная конкурирующая гипотеза как объяснение первоначальных
данных может быть “исключена”. Если отношения достаточно хорошо
выдерживают такое контролирование, они принимаются как обоснованные.
Важно помнить, что мы могли бы найти такой пример, когда отношения,
представленные в табл. 16.1, стали бы статистически незначимыми, и тогда мы
создали бы отдельные таблицы сопряженности для мужчин и женщин. В таком
случае исследователь может сказать, что первоначально предложенные
отношения не прошли процедуры контроля и что альтернативная
конкурирующая гипотеза не может быть исключена.
Таким образом, мы провели простейший многомерный анализ, используя
технику, предназначенную для бипараметрического анализа. Мы можем
продолжить эту логическую цепочку и оценить другие альтернативные
конкурирующие гипотезы, применив для контролирования две или более
дополнительные переменные одновременно. Чтобы проиллюстрировать это, в
качестве альтернативной конкурирующей гипотезы предположим, что расовые
различия между белыми и небелыми (и с точки зрения политического уровня, и
с точки зрения вероятности посещения колледжа) несомненно формируют
указанные в табл. 16.1 отношения между посещением колледжа и
мировоззрением. Чтобы одновременно проверить влияние расовых различий и
различий по половому [c.440] признаку на указанные отношения, мы должны
будем составить четыре таблицы сопряженности, представляющие эти
отношения для: белых мужчин, белых женщин, небелых мужчин и небелых
женщин.
Таблица 16.2.
Гипотетические отношения между получением образования в колледже и
политическим мировоззрением для мужчин
Образование
в колледже
Мировоззрение
Либералы (%) Консерваторы
(%)
Общее число
респондентов
Получили
Не получили
Всего:
33……………(5)
67…………(10)
100…………(15)
57……………(20)
43……………(15)
100…………(35)
(25)
(25)
(50)
Таблица 16.3.
Гипотетические отношения между получением образования в колледже и
политическим мировоззрением для женщин
Образование
в колледже
Мировоззрение
Либералы (%) Консерваторы
(%)
Общее число
респондентов
Получили
Не получили
Всего:
43……………(15)
57……………(20)
100…………(15)
67……………(10)
33………………(5)
100……………(15)
(25)
(25)
(50)
При условии правильной обработки, такой подход к многомерному анализу
может очень хорошо помочь в оценке гипотез. Однако у него есть
существенные ограничения. Во-первых, он очень громоздкий, и получаемые
результаты трудно интерпретировать, если используемые переменные имеют
много возможных уровней. Именно поэтому непрактично применять это метод
для анализа интервальных переменных; его также трудно использовать для
многих номинальных и одноуровневых переменных. Например, чтобы сравнить
независимую и зависимую переменную, каждая из которых содержит 5
уровней, и при этом проконтролировать их с помощью третьей переменной с 10
уровнями, потребуется анализ 10 таблиц по [c.441] 25 ячеек в каждой. И хотя в
нашем распоряжении может иметься исключительно большая и разнообразная
выборка, множество ячеек в таблицах останется незаполненным, что может
сделать невозможным вычисление некоторых мер связи и значимости. Мы
могли бы попытаться избежать этого путем объединения определенных
категорий переменных, чтобы уменьшить число уровней и сократить число
необходимых таблиц и ячеек (как в том случае, когда мы сократили меру “годы
учения” до дихотомии “менее 12 лет” и “12 лет и более”). Тем не менее, это
означает, что имеющаяся в первоначальных данных часть информации, которая
может оказаться важной, будет потеряна, что может привести к искажению
результатов. Более того, с такой же проблемой мы можем столкнуться даже и
после того, как мы объединили категории, – в том случае, если мы попытаемся
сразу добавить для контроля несколько переменных, чтобы проверить

комбинированный эффект различных переменных. Во-вторых, даже если мы
можем выполнить такой анализ, его результаты трудно будет ввести в оборот,
так как модель выглядит достаточно сложно, и кроме того, не существует
обобщающей статистики, позволившей бы суммировать полученные в итоге
данные.
К счастью, существует ряд статистических приемов, которые предназначены
специально для многомерного анализа и которые можно использовать для
решения широкого круга задач; их результаты сравнительно легко
интерпретируются. Они особенно ценны, так как обладают возможностями
проверки гипотез (позволяют анализировать взаимосвязи двух переменных с
учетом воздействия других переменных на каждую константу), но главное их
достоинство заключено в тех способах, которыми они помогают нам уяснить
сложную и хрупкую сеть взаимосвязей, в которую вплетены социальные
явления. В этой главе мы познакомим вас с тремя наиболее часто
используемыми способами многомерного анализа, с тем чтобы вы знали, когда
и как применять их в своих исследованиях, и, читая научные труды, могли
судить о том, как их применяют другие. Мы выбрали эти методы из всего
множества возможных потому, что (1) они широко применяются, (2) они
иллюстрируют некоторые основные принципы многомерного анализа и (3) все
они основаны на [c.442] одних и тех же базовых математических приемах и
могут быть поэтому объяснены легче, чем те, которые требуют привлечения
разных математических приемов. [c.443]
МНОЖЕСТВЕННАЯ РЕГРЕССИЯ
Все, что говорилось о двумерной корреляции и регрессии в гл.15, может быть
распространено на те случаи, когда вы хотите изучить взаимосвязи между
одной независимой (НП) и несколькими зависимыми переменными (ЗП). Цель
множественной регрессии – обеспечить (1) подсчет независимого воздействия
изменений в значениях каждой ЗП на значения НП и (2) эмпирический базис,
чтобы предсказать значения зависимой переменной на основе знания
совместного влияния НП.
Анализ начинается с составления уравнения, которое, на ваш взгляд, точно
описывает исследуемые вами причинные связи. Поскольку это уравнение
можно рассматривать как модель исследуемого процесса, это шаг
расценивается как построение модели. Оно заключается в переводе вашей
вербальной теории явления на язык математических уравнений. Общая
формула множественной регрессии такова:
Y’ = а
0
+ b
1
X
1
+ b
2
X
2
…
+…b
n
X
n
+ e.
В ней вы можете узнать несколько расширенное уравнение двумерной
регрессии, описанной в гл.15. Понимание этого уравнения может облегчить
конкретный пример.
