Макаров Е.Г. Сопротивление материалов
Подождите немного. Документ загружается.


Рис. 12.13. Определение критических нагрузок на ступенчатый стержень
Приведенная программа позволяет приближенно определять
критическую нагрузку при действии нескольких сил и нескольких
участках различной формы сечения
. Степень полинома определяем,
исходя из числа граничных условий и
"на глазок" по виду графика
полинома и его производных
.
Продольно-поперечный изгиб. Программа ustoi3
Рассмотрим стальной стержень прямоугольного поперечного сечения,
закрепленный на двух шарнирных опорах (схема Эйлера). Стержень
нагружен осевой сжимающей и поперечной изгибающей нагрузками.
Рассчитаем прогиб стержня при двух видах поперечной нагрузки:
равномерно распределенной по длине стержня,
сосредоточенной.
Расчеты ведем без учета размерностей, так как функция решения
дифференциальных уравнений
odesolve не может работать с
размерными величинами.
Схема нагружения и исходные данные для расчета стержня с
поперечной распределенной нагрузкой показаны на рис. 12.14.
Рис. 12.14. Схема нагружения и исходные данные для расчета
Расчет прогиба, поперечной силы и изгибающего момента показан на
рис. 12.15.
Для справки там же приведено значение критической силы,
вычисленной по формуле Эйлера. Сжимающая сила взята
кр
0,8
F
F≈ .
На рис. 12.16 приведены графики изменения по длине стержня
прогиба, поперечной силы и изгибающего момента. Там же приведен
расчет максимального напряжения в стержне.
121
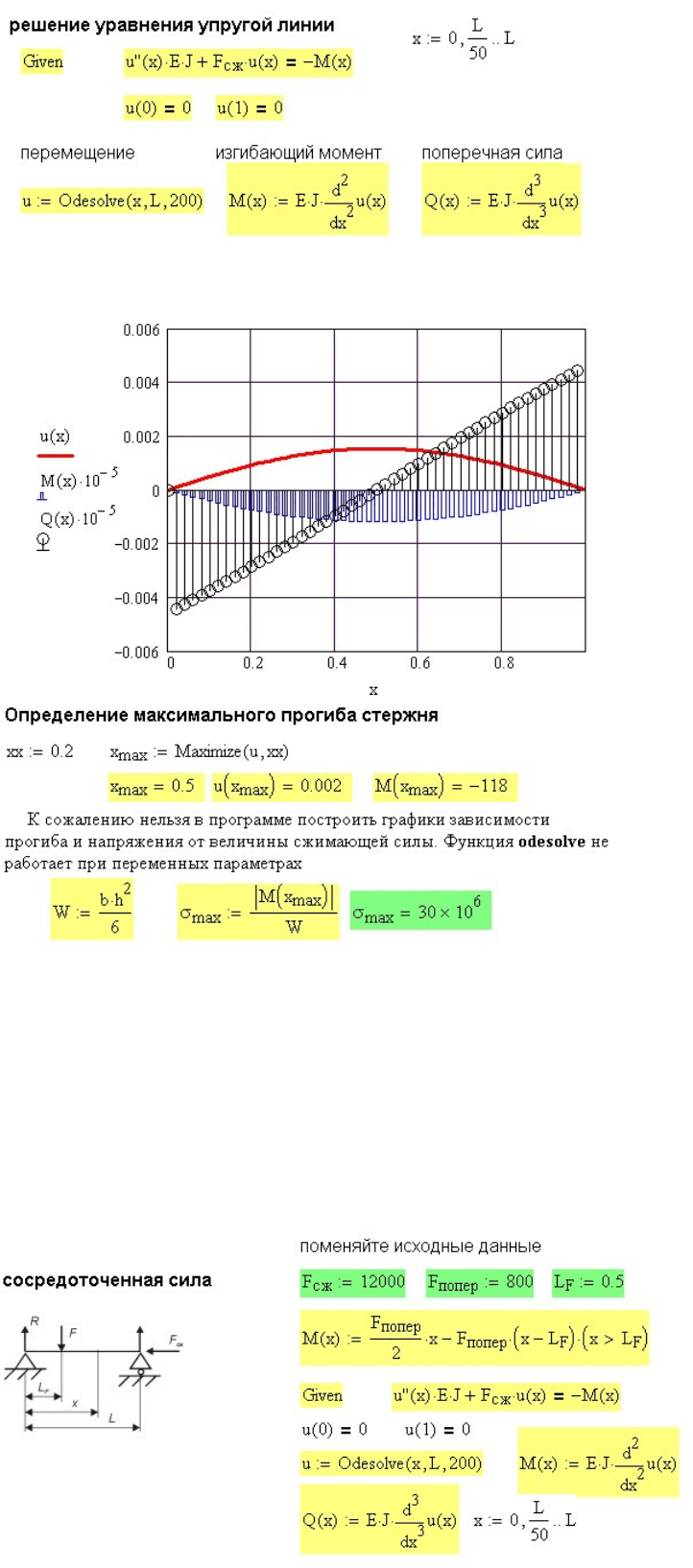
Рис. 12.15. Расчет прогиба, поперечной силы и изгибающего момента
Рис.12.16. Результаты расчета стержня с поперечной распределенной нагрузкой
Для определения максимального изгибающего момента использована
функция
maximize, хотя делать это не обязательно. По симметрии
максимум находится посередине стержня при
0,5x
=
м. Использование
функции
maximize позволяет использовать программу при различных
поперечных нагрузках.
Расчет того же стержня при другой нагрузке показан на рис. 12.17.
Вместо распределенной нагрузки приложена сосредоточенная сила
F
.
Результаты расчета приведены на рис. 12.18
Рис. 12.17. Расчет стержня с поперечной силой.
122

Рис.12.18. Результаты расчета стержня с поперечной силой
К сожалению нельзя в программе построить графики зависимости
прогиба и напряжения от величины сжимающей силы. Функция
odesolve не работает при переменных параметрах.
Рис. 12.19. Использование дифференциального уравнения 4-го порядка при продольно-
поперечном изгибе стержня c поперечной распределенной нагрузкой
Рис. 12.20. Использование дифференциального уравнения 4-го порядка при продольно-
поперечном изгибе стержня с поперечной сосредоточенной силой
123
Для расчета стержня на продольно-поперечный изгиб, кроме
дифференциального уравнения второго порядка, можно использовать
дифференциальные уравнения четвертого порядка (формулы к-12.16 и
к-12.17). Такой расчет показан на рис. 12.19 для поперечной
распределенной нагрузки и на рис. 12.20 для поперечной
сосредоточенной силы. Результаты расчета такие же, как при
использовании дифференциального уравнения второго порядка и на
рисунках здесь не приведены. Зато они включены в программу
ustoi3 в
электронной книге.
Поскольку в уравнение (12. 17) входит только интенсивность
поперечной распределенной нагрузки , сосредоточенную силу надо
заменить нагрузкой, распределенной на малой длине стержня .
q
Δ
Величина может быть сколь угодно малой. На остальной части
стержня приходится приложить очень маленькую распределенную
нагрузку. В противном случае Mathcad отказывается решать задачу.
Δ
Поскольку дифференциальное уравнение — четвертого порядка,
внутри вычислительного блока
given – odesolve записаны 4
граничных условия: равенство нулю прогиба стержня и равенство
нулю изгибающих моментов (вторых производных от прогиба) в
точках закрепления.
Решая дифференциальное уравнение четвертого порядка, не забывайте,
что даже для Mathcad это чрезвычайно сложная задача. Результат
вычислений (или отсутствие результата) зависит от выбора начального
приближения, способа решения, числа шагов вычислений.
124
Для главы 13. Расчет тонкостенных
оболочек
Пример расчета тонкостенной оболочки.
Программа
obolochka1
Для оболочки, состоящей из трех частей: конической, цилиндрической
и сферической (рис. 13.1), при заданных габаритных размерах и
внутреннем давлении найти толщину стенки.
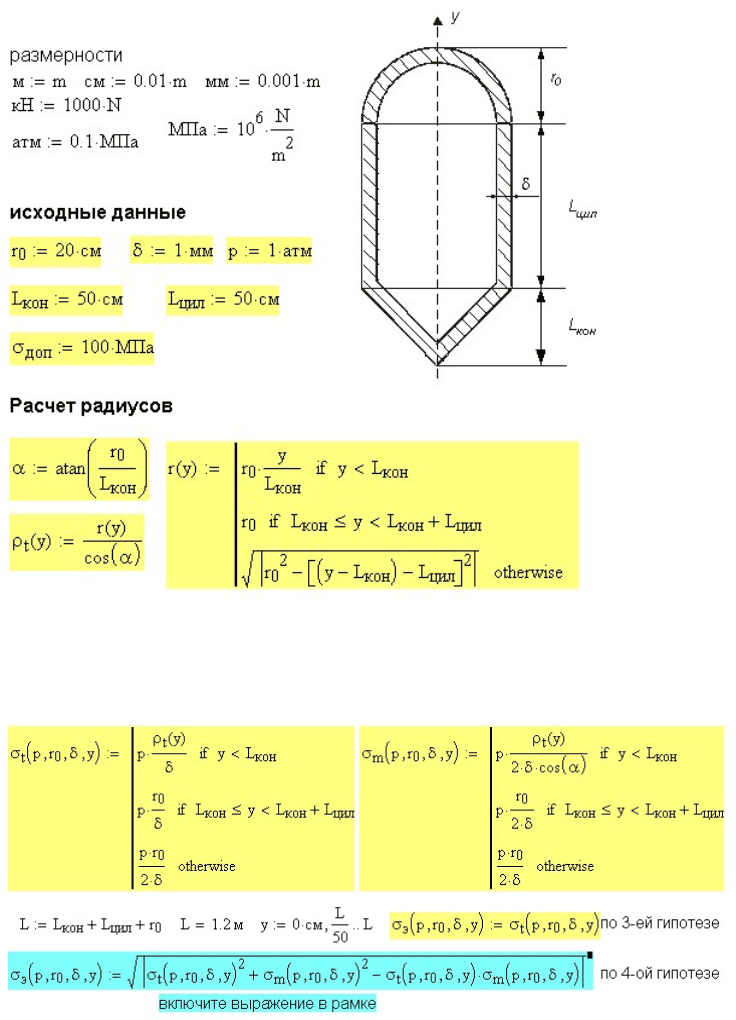
Рис. 13.1. Схема оболочки и исходные данные к ее расчету
Расчет ведем с учетом размерностей, поэтому в начале программы
приведены производные размерности.
Рис. 13.2. Расчет напряжений в тонкостенной оболочке
Далее приведены исходные данные для расчета (рис. 13.1): радиус
цилиндрической части , давление
0
r
p
, длины цилиндрической и
конической частей оболочки
кон
L
и
цил
L
, приближенное значение
толщины оболочки
δ
(для вывода промежуточных результатов
расчетов), допускаемое напряжение
доп
σ
.
Для построения графиков напряжений найдена зависимость радиуса
поперечного сечения оболочки от координаты ()ry
y
(вдоль оси
оболочки) для конической, цилиндрической и сферической частей
оболочки. Найден радиус кривизны конической части
()
t
y
ρ
.
125
При вычислении радиуса
()
r
y
сферической части подкоренное
выражение взято по модулю, так как в процессе вычислений при
равенстве нулю подкоренного выражения машинный нуль округляется
то в положительную, то в отрицательную сторону, при этом программа
выдает ошибку.
Выражения для тангенциальных
t
σ
и меридиональных напряжений
, как и радиус
m
σ
()
r
y
записаны в виде подпрограмм.
При записи программ с условиями надо строго следить, чтобы были
определены значения функции при всех значениях аргумента, уделяя
особое значение знакам < и
≤.
По значениям и определяются эквивалентные напряжения по
третьей или по четвертой гипотезам прочности. Выражение для
эквивалентных напряжений по четвертой гипотезе в программе
выключено. Включите его и посмотрите на результаты расчета.
t
σ
m
σ
Все выражения для напряжений записаны с четырьмя параметрами
0
(
,,
)
pr
y
σδ,. Такая форма записи делает программу расчета
универсальной, позволяя определять напряжения при любых
значениях этих параметров.
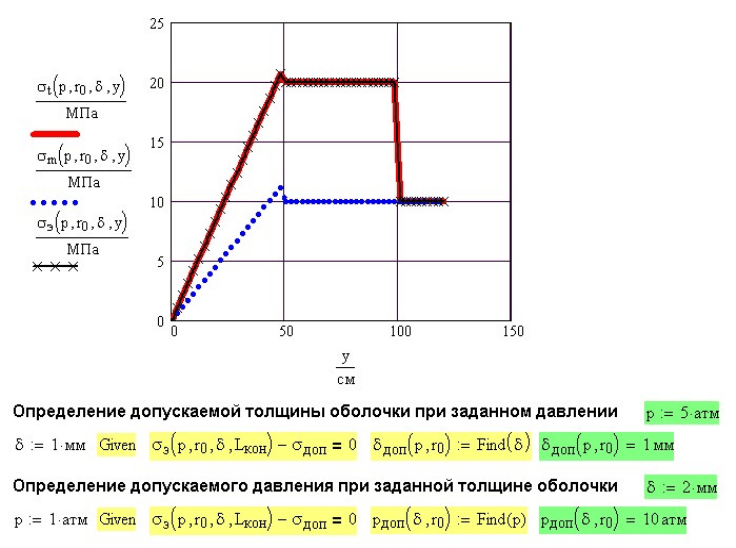
Рис. 13.3. Распределение напряжений вдоль оси оболочки
На рис. 13.3 показаны графики изменения напряжений
э
,,
tm
σ
σσ по
длине оболочки при заданных в начале программы значениях
0
,,
p
r
δ
.
На том же рисунке внизу показано определение из условия прочности
допускаемой толщины оболочки с помощью вычислительного блока
given – find. Вычислительному блоку предшествует начальное
приближение толщины
δ
. Вариируя исходные значения
p
и ,
можно определить допускаемую толщину оболочки
0
r
доп
δ
при любых
значениях давления и радиуса оболочки.
Из условия прочности можно определить и давление
p
при заданных
толщине
δ
и радиусе .
0
r
Функция
root с подобной задачей не справилась. В силу особенностей
внутреннего алгоритма этой функции она выводит результаты расчета
далеко не для всех значений аргументов.
Щелкните правой кнопкой мыши на слове
find. В контекстном меню
есть возможность выбора способа решения системы уравнений:
Linear
или
Nonlinear. Выберите любой из трех методов Nonlineer. Такой
возможности нет при использовании функции
root.
126
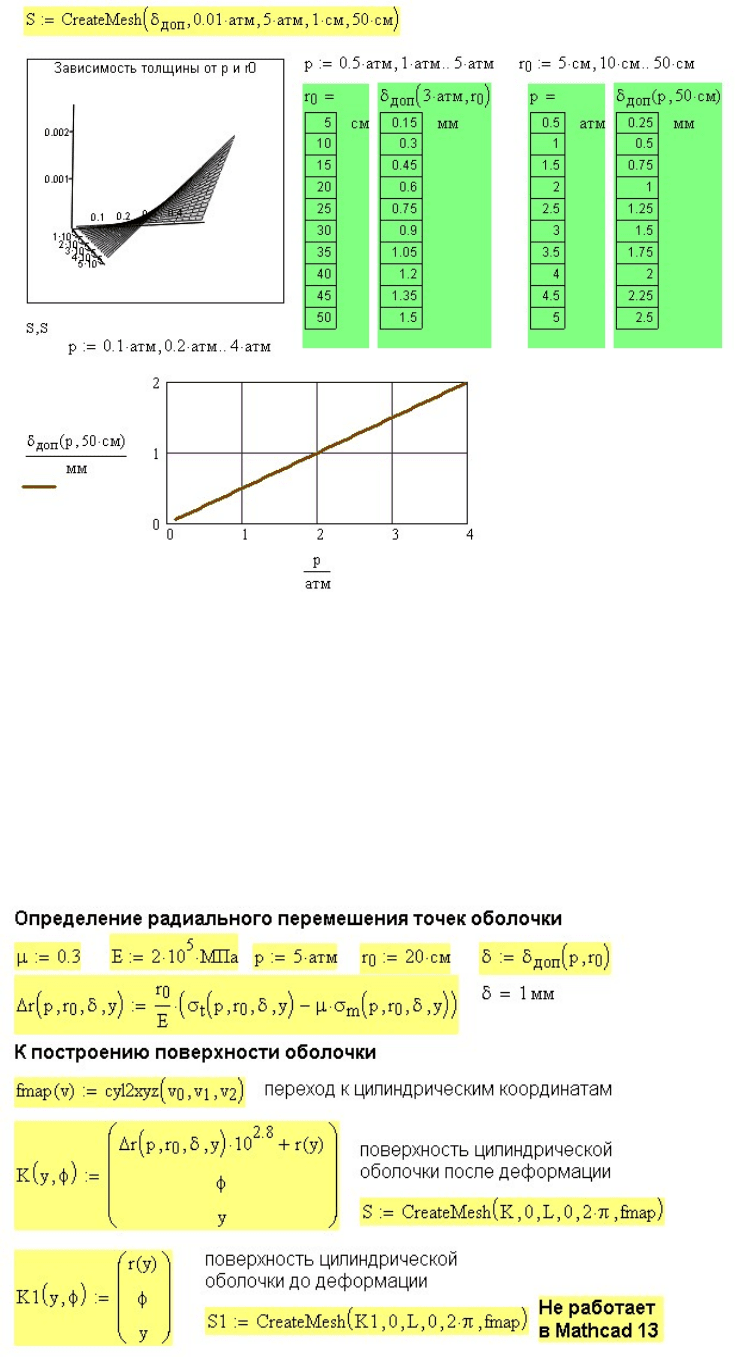
На рис. 13.4 выведен трехмерный график зависимости допускаемой
толщины оболочки от давления и радиуса оболочки. График построен
по массиву значений, созданному функцией
CreateMech, параметрами
которой являются допускаемая толщина
доп
δ
и числовые диапазоны
изменения давления
p
и радиуса оболочки .
0
r
Рядом с графиком выведены таблицы значений
доп
δ
для различных
p
и .
0
r
Рис. 13.4. Результаты расчета тонкостенной оболочки
Внизу рис. 13.4 выведен двумерный график зависимости
доп
δ
от . p
Обратите внимание на запись диапазона значений дискретной
переменной с размерностью и численного аргумента с размерностью.
На рис. 13.5 приведен расчет радиальных перемещений по формуле (к-
13.10). Перемещения определяются для допускаемой толщины
оболочки.
r
Δ
Чтобы определить перемещения при иной толщине оболочки, ее надо
задать выше места определения перемещений.
Рис. 13.5. Определение радиальных перемещений оболочки
127
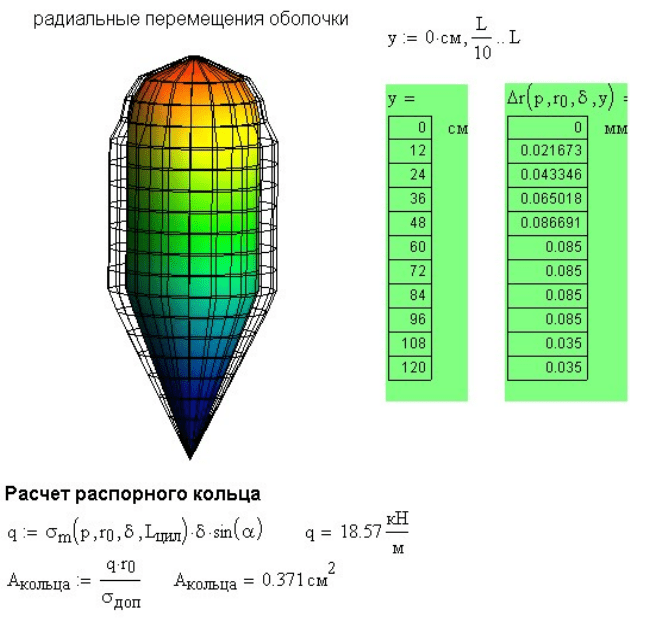
На рис. 13.6 выведены значения рассчитанных перемещений и
построен график поверхности оболочки до и после деформации.
Подготовка к построению поверхности показана на рис. 13.5.
Произведен переход от прямоугольных к цилиндрическим
координатам с помощью встроенной функции
cyl2xyz, которая входит
параметром в функцию
CreateMech, создающую массив значений для
построения поверхности. Параметрами функции
CreateMech
являются — функция полярных координат поверхности, пределы
изменения координат по углу и по по оси оболочки, функция
преобразования координат
K
fmap.
Промежуточная функция
(
,
Ky
θ
) задает вектор координат точек
поверхности (сверху вниз: вдоль радиуса, по углу, по оси оболочки).
Рис. 13.6. Вид оболочки до и после деформации
Поскольку радиальные перемещения оболочки малы, для наглядности
они увеличены с помощью масштабного коэффициента 10
2,8
. Такая
форма записи масштабного коэффициента очень удобна. Она
позволяет, меняя показатель степени, быстро менять масштаб графика.
В заключение расчета определена площадь распорного кольца для
разгрузки оболочки от изгибающего момента, в месте перехода от
конической к цилиндрической части оболочки.
Получилась элегантная и универсальная программа для расчета любой
тонкостенной оболочки. Для оболочки, составленной из других
элементов, внесите соответствующие изменения в подпрограммы
определения напряжений и радиусов кривизны на рис.13.1 и 13.2.
Оценка краевого эффекта в тонкостенной
оболочке. Программа
obolochka2
Расчет ведем в системе СИ без учета размерностей, так как функция
odesolve не может работать с размерными величинами.
Исходные данные для расчета и основные формулы, перечисленные в
теоретическом курсе (раздел 13.4), приведены на рис. 13.7.
Дифференциальное уравнение четвертого порядка решается функцией
odesolve.
128
Граничные условия: равенство нулю прогиба и угла поворота (u и )
в заделке (в жестком фланце), равенство нулю поперечной силы и
изгибающего момента (
u и
u
′
′′′
u
′
′
) вдали от заделки.
Результаты расчета приведены на рис. 13.8. Вблизи жесткого фланца
наблюдается резкий всплеск изгибающего момента и резкое
уменьшение прогиба до нуля (краевой эффект). Размер зоны краевого
эффекта мал.
При
100
r
δ
∼
0
4
r
h ∼
,
при
0
20
r
δ
∼
0
2
r
h ∼
,
при
0
10
r
δ
∼
0
3
4
hr∼
.
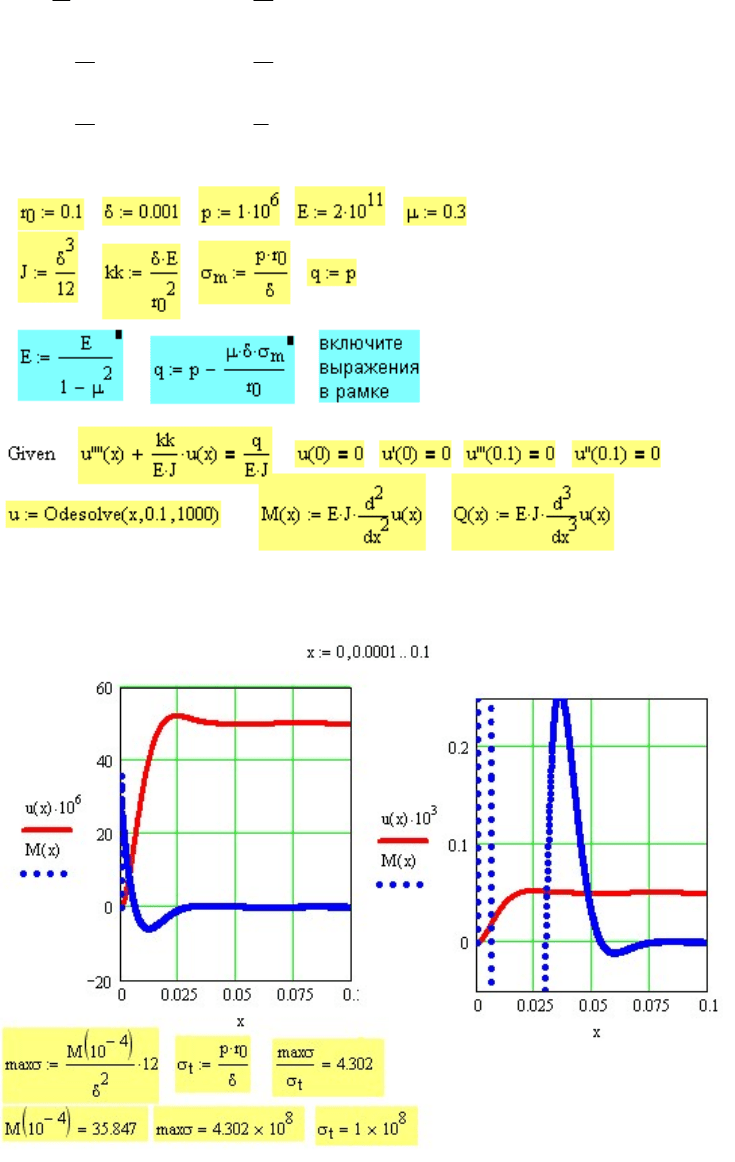
Рис. 13.7. Расчет радиальных перемещений в оболочке с жестким фланцем u
Рис. 13.8. Краевой эффект в цилиндрической оболочке с жестким фланцем
Функции прогиба и изгибающего момента имеют волновой быстро
затухающий характер. Амплитуда каждой последующей полуволны
примерно в 10 раз меньше амплитуды волны предыдущей. На рис 13.8,
слева изображены полные графики прогиба и изгибающего момента
u
M
. Справа те же графики в увеличенном масштабе. При увеличении
масштаба в 10 раз на графике появляется очередная полуволна.
129
Внизу рис. 13.8 приведен расчет максимальных напряжений в месте
соединения оболочки с фланцем. Они в 4 раза превышают напряжения
вдали от края оболочки.
Следует отметить, что в этом расчете не учтено влияние
меридионального напряжения
m
σ
, которое растягивает вырезанную из
оболочки полоску. При этом поперечный размер полоски уменьшается,
что эквивалентно уменьшению упругой реакции оболочки или, что то
же самое, уменьшению давления в оболочке.
Учет меридионального напряжения несколько уменьшает краевой
эффект, но не меняет характер краевого эффекта. Максимальные
напряжения в месте соединения оболочки с фланцем уже не 4, а только
в 3 раза превышают напряжения вдали от края оболочки.
На рис. 13.7 в программу расчета включены два слагаемых,
уточняющих расчет. Они в программе выключены. Включите их и
посмотрите результаты расчета.
130
