Мадиев Н.М. Простой вывод фильтра Калмана
Подождите немного. Документ загружается.


1
Мадиев Н.М.
ПРОСТОЙ ВЫВОД ФИЛЬТРА КАЛМАНА
В соответствии с теорией оценки вектора состояний (или иначе – ненаблюдаемого оцени-
ваемого сигнала) являются несмещенными, имеют минимальную невязку и уровень
шумов в случае, если точно заданы начальное состояние и параметры системы. В
фильтрах Калмана стремятся редуцировать измеряемый сигнал к виду, который он имел
бы на выходе идеального прибора. Вместе с тем на практике часто оказывается
достаточно редуцировать сигнал к виду, который он имел бы на выходе прибора c
заданными характеристиками при контролируемом уровне шумов.
Предлагаемый ниже подход позволяет получить в виде частного случая фильтр Калмана.
Рассмотрим дискретную линейную систему. Пусть схема измерения сигнала имеет вид
tttt
xAy
n
+= (1)
где вектор
m
t
y ÂÎ – измеряемый сигнал, размерности m; матрица
nm
t
A
´
ÂÎ – описывает
реальный прибор;
m
t
ÂÎ
n
– случайный вектор, той же размерности, определяющий
погрешность измерений (шум) с нулевым средним Eν
t
= 0, и известной ковариационной
матрицей
mm
t
R
´
ÂÎ .
Считаем, что искомый сигнал
t
x связан с сигналом в предыдущий момент времени
соотношением
ttttt
xx
w
G+F=
+1
, (2)
Где
nn
t
´
ÂÎF и
nn
t
´
ÂÎG – заданные матрицы, размерности
n
n
´
;
n
t
ÂÎ
w
– случайный
вектор с нулевым средним 0=
t
E
w
и заданной ковариационной матицей
nn
t
Q
´
ÂÎ .
Допустим, что шумы
t
n
и
t
w
не коррелированны, и что известно начальное состояние
системы: ковариационная матрица ошибки оценивания
nn´
ÂÎS
0
, матрицы ,
0
F ,
0
G
0
Q и
вектор оценки искомого сигнала
0
ˆ
x в момент времени t = t
0
.
Запишем линейное преобразование измерения (1):
ttttttttttttttt
KxIAKxIKxAKyK
nn
+-+=+= )( , (3)
Где
mn
t
K
´
ÂÎ , а
nn
t
I
´
ÂÎ – матрица, описывающая некоторый гипотетический прибор,
наделенный необходимыми заданными свойствами, то есть, I
t
– прибор, который по своим
характеристикам лучше, чем прибор A
t
, в частности, I
t
может быть идеальным прибором
(то есть, равным единичной матрице II
t
= ). Используя выражения (2) и (3), мы можем
записать, что сигнал на выходе прибора I
t
определяется из соотношения
ttttttttttttt
KxAKIyKxI
nw
-G+F-+=
----
))((
1111
(4)
Пусть
t
x
ˆ
есть оценка искомого сигнала x
t
, заданная в виде
11
ˆ
)(
ˆ
--
F-+=
ttttttttt
xAKIyKxI (5)

2
Вычитая из (4) равенство (5), получим вектор ошибок оценивания, такой, что
tttttttttttttt
KxAKIxxIxI
nw
-G+F-=-=
----
)
~
)(()
ˆ
(
~
1111
Ведем обозначение: пусть
nn
t
P
´
ÂÎ – ковариационная матрица вида
T
ttt
T
tttt
QP
111111 ------
GG+FSF= , (6)
Тогда ковариационная матрица ошибки оценивания искомого сигнала при оценке (5)
имеет вид
T
ttt
T
tttttttt
KRKAKIPAKI +--=S )()( . (7)
Матрицу K
t
найдем из следующей вариационной задачи:
min)(
2
2/1
®-=
ttttt
PAKI
e
d
, при условии
e
£
2
2/1
tt
RK . (8)
Если
e
t
K есть ее решение, то оценками исходного сигнала x
t
будут сигналы вида
e
t
K y
t
. Эти
сигналы при контролируемом уровне шума, не превышающем
e
, с точностью до
e
d
t
будут
совпадать с сигналами на выходе заданного прибора I
t
.
Теорема. Пусть схема измерения сигнала описывается уравнениями (1) и (2), заданы
начальные условия: вектор
t
x
ˆ
и матрицы
0
S , ,
0
F ,
0
G
0
Q . Тогда оценка искомого сигнала
на выходе заданного прибора I
t
в этой системе в момент времени k по наблюдениям ,
1
y
,
2
y …,
k
y , минимизирующая критерий
tt
xxE
ˆ
- при заданным уровне шумов
e
(8),
задается рекуррентными уравнениями (5), где матрица K
t
имеет вид:
1
)(
-
+=
t
T
ttt
T
tttt
RAPAAPIK
l
при
e
ll
= , 0 <
e
<
0
e
,
и
(
)
+
=
2/12/1
ttttt
PAPIK при
e
³
0
e
.
где
(
)
2
2/12/12/1
0 ttttt
RPAPI
+
=
e
; здесь
+
t
A – псевдообратная матрица.
e
l
– единственный корень уравнения
( )
(
)
.,
2
2/1
1
2
2/1
ellh
=+==
-
tt
T
ttt
T
tttttt
RRAPAAPIRKI
При этом уровень шума определяется как
( )
î
í
ì
=
,0
,
,
e
e
lh
t
I
0 <
e
<
0
e
0
ee
³
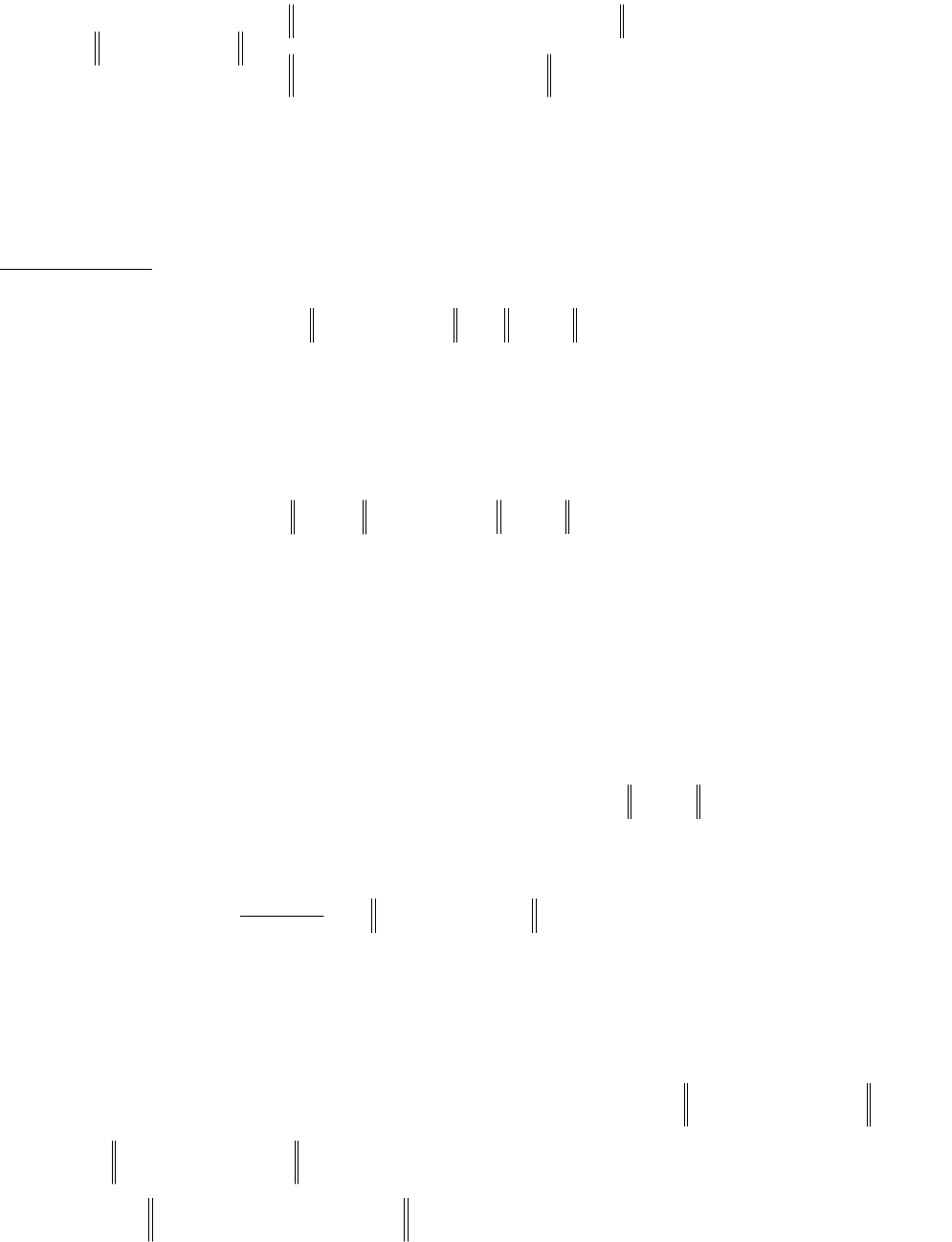
3
А невязка
( )
(
)
( )
ï
î
ï
í
ì
-
+-
=-=
+
-
2
2/12/12/1
2
2/11
2
2/1
)(
,)(
)(,
ttttttt
ttt
T
ttt
T
tttt
ttttt
PAPAPII
PARAPAAPII
PAKII
l
lr
И для l > 0
(
)
t
Id ,
lhl
+
(
)
.0, =
t
Id
lr
Доказательство
. Функция Лагранжа выпуклой задачи (8) имеет вид:
(
)
,),(
2
2/1
2
2/1
ttttttt
RKPAKIKL
ll
+-= ,0
³
l
Приравняв производную по K
t
функции Лагранжа нулю, получим:
(
)
,022 =+--
tt
T
ttttt
RKAPAKI
l
(9)
,0
³
l
,0
2
2/1
=
÷
ø
ö
ç
è
æ
-
el
tt
RK
,0
2/1
£-
e
tt
RK (10)
Условия (9) и (10) определяют седловую точку функции
(
)
t
KL ,
l
и при
0
³
e
– решение
задачи (8). Из выражения (9) находим, что
1
)(
-
+=
t
T
ttt
T
tttt
RAPAAPIK
l
(11)
где P
t
определяется выражением (6).
Уровень шума
(
)
tt
I,
lh
, определяемый соотношением
( )
2
2/1
,
ttt
RKI =
lh
, не возрастает
при 0 < l <
¥
. Пусть
t
T
ttt
RAPAS
l
l
+= , тогда
(
)
2
2/11
2
,
--
-=
ll
l
l
h
SRSAPI
d
Id
t
T
ttt
t
, (12)
и выражение (12) равно нулю, тогда и только тогда, когда )()(
t
T
ttt
RAPI ÀÌÂ . Здесь ядро
матрицы H – суть множество векторов, которое H отображает в нуль:
{
}
0:)( ==À HxxH .
Если такое включение не имеет место, то
(
)
tt
I,
lh
строго монотонно убывает на 0 < l <
¥
,
причем, учитывая, что
(
)
1
0
lim
-
®
+
+= IHHHH
TT
l
l
, имеем:
( )
(
)
2
2/12/12/1
0
,lim
tttttt
RPAPII
+
®
=
lh
l
.
Пусть
(
)
2
2/12/12/1
0 ttttt
RPAPI
+
=
e
. Тогда если 0 <
e
<
0
e
, то уравнение относительно l
вида
( )
(
)
ellh
=+=
-
2
2/1
1
,
tt
T
ttt
T
tttt
RRAPAAPII имеет единственное решение l = l
e
. Тогда
tt
KK =
e
есть решение задачи (8).
e
ll
= , 0 <
e
<
0
e
,
e
³
0
e
.
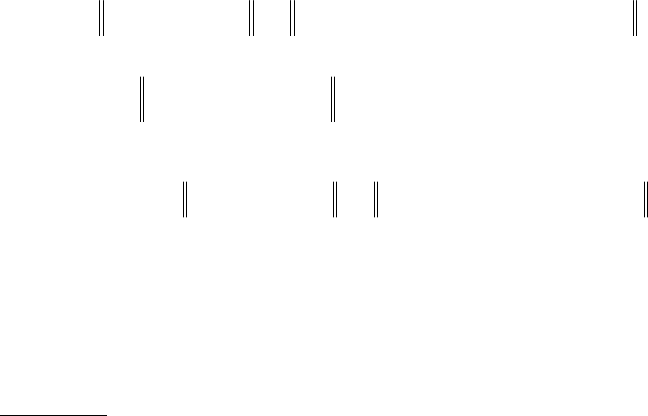
4
Отметим, что в этом случае невязка
(
)
t
I,
lr
в силу равенства (11) примет вид:
( )
(
)
2
2/11
2
2/1
][)(,
ttt
T
ttt
T
ttttttttt
PARAPAAPIIPAKII
-
+-=-=
llr
,
e
ll
= , 0 <
e
<
0
e
,
При
e
³
(
)
2
2/12/12/1
0 ttttt
RPAPI
+
=
e
условие (10) выполняется для
l
= 0. Тогда, используя
определение псевдообратной матрицы, получим, что
(
)
+
=
2/12/1
ttttt
PAPIK
e
, следовательно,
невязка
( )
(
)
2
2/12/12/1
2
2/1
)()(,
tttttttttttt
PAPAPIIPAKII
+
-=-=
lr
,
e
³
0
e
.
Выполнение закона сохранения
(
)
t
Id ,
lhl
+
(
)
0, =
t
Id
lr
проверяется непосредственной
подстановкой. Действительно,
(
)
llh
dRKId
ttt
=, ;
(
)
(
)
llr
dAPAKIId
T
tttttt
--=, ;
(
)
0=+-=++-=++-
T
ttt
T
tttt
T
tttt
T
ttttt
T
tttt
T
ttt
APIAPIRAPAKAPIRKAPAKAPI
ll
.
Замечание
. Из соотношения (11) видно, что при II
t
= и l = 1 получается коэффициент
усиления K
t
из фильтра Калмана-Бьюси.
Литература
1. Мадиев Н.М. Повышение разрешающей силы прибора и фильтры Калмана-Бьюси.
Технические и программные средства автоматизации научных исследований. Алма-
Ата. Наука, 1987. стр. 78-84.
