Ляндзберг А.Р., Надольская Н.И. Механика. Техническая механика. Расчет вала на прочность

Подождите немного. Документ загружается.

При изгибе, если сила или момент изгибают балку вверх

(т.е. выпуклостью вниз), то они принимаются со знаком

плюс,

если сила или момент изгибают балку вниз (т.е. выпуклостью

вверх), то они принимаются со знаком

минус. Данное правило

иногда формулируют еще и так: эпюра моментов строится на

сжатом волокне.

III.

Правила построения эпюр сил и моментов.

1). Сосредоточенная сила вызывает скачок на эпюре попе-

речных сил и излом на эпюре изгибающих моментов. Направле-

ние скачка выбирается по «главному правилу», величина скачка

равна величине силы.

2). Сосредоточенный момент вызывает скачок на эпюре

изгибающих моментов и не влияет на эпюру поперечных сил.

Направление скачка выбирается по «главному правилу», вели-

чина скачка равна величине момента.

3). Если на балке нет ни распределенных, ни сосредото-

ченных сил, то эпюра поперечных сил равна нулю, а эпюра из-

гибающих моментов постоянна (параллельна оси).

4). Если на участке балки нет распределенных, но есть со-

средоточенные силы, эпюра поперечных сил постоянна (парал-

лельна оси), а эпюра изгибающих моментов – наклонная прямая.

5). Если на участке есть распределенные силы, то эпюра

поперечных сил – наклонная прямая, эпюра изгибающих момен-

тов – парабола. Выпуклость параболы направлена против дей-

ствия распределенных сил, т.е. если распределенные силы на-

правлены вниз, строим эпюру изгибающих моментов выпукло-

стью вверх, и наоборот.

6). Изменение эпюры поперечных сил на участке равно

воздействию распределенных сил: ΔQ = ql.

7). Изменение эпюры изгибающих моментов на участке

равно площади под эпюрой поперечных сил на этом участке (с

учетом знака): ΔМ

= S

ЭQ

8). Если в какой-либо точке эпюра поперечных сил пере-

секает ось (равна нулю), на эпюре изгибающих моментов возни-

кает экстремум. В этом случае проводим дополнительное сече-

ние через данную точку и рассматриваем отдельно участки

справа и слева от экстремума.

Применим данные правила к построению эпюр внутрен-

них сил и моментов вала.

1). Первоначально строим эпюру крутящих моментов.

Найденный для колеса D

крутящий момент на валу составляет

кр

= 955 Н·м, это значение мы и откладываем от нулевой ли-

нии.

Далее в точке 3 на колесе D

левом (далее будем обозна-

чать данную точку «3Л») крутящий момент, как уже было ска-

зано выше, понижается вдвое, так как передача вращения на ве-

домый вал идет через два колеса одновременно. Величина мо-

мента между колесами D

левым и правым составляет M

кр2

955/2 = 477,5 Н·м.

Наконец, в точке 3 на колесе D

правом (далее будем обо-

значать данную точку «3П») крутящий момент падает до нуля,

т.к. полностью передается на следующий вал.

Построенные значения отмечаются на эпюре, сама эпюра

штрихуется и подписывается «ЭМ

кр

» (т.е. «эпюра крутящего

момента»).

2). Строим эпюру сил по оси OX. Нами уже были получе-

ны и отложены на схеме величины всех активных и реактивных

сил, действующих на вал по оси OX. Теперь согласно этим си-

лам проведем построение.

Обратим внимание, что на вал ни на каком участке не

действует распределенная нагрузка, а действуют только сосре-

доточенные силы. Следовательно, правила (3), (5) и (6) к данной

балке не относятся. В то же время, согласно правилу (4), вели-

чина поперечных сил на каждом отдельном участке будет по-

стоянна, а ее эпюра будет проходить параллельно оси. Осталось

применить правило (1), согласно которому и найдем конкретные

значения сил на участках.

В точке 1 на вал действует тангенциальная сила F

τ1

9555 Н. Откладываем ее на эпюре от нуля. Направление скачка

выбираем по «главному правилу», а именно: поскольку мы на-

чали построение слева направо, то направление скачка соответ-

ствует направлению силы.

До точки 2 на вал не действуют никакие новые внешние

силы, поэтому величина внутренних сил в 9555 Н сохраняется

(эпюра идет параллельно оси).

В точке 2 на вал действует сила R

= 19662 H, направлен-

ная вниз. Из существующей силы в 9555 Н отнимаем 19662 H

(т.е. строим скачок величиной 19662 H вниз) и находим новое

значение силы: -10107 Н. Данное значение сохраняется (эпюра

параллельна оси) до точки 3 (левой).

В точке 3Л на вал действует сила F

= 7298 H. Отклады-

ваем от величины -10107 Н скачок в 7298 H вверх, получаем но-

вое значение -10107 + 7298 = -2809 Н. Это значение сохраняется

(эпюра параллельна оси) до точки 3П.

В точке 3П на вал еще раз действует сила F

= 7298 H.

Откладываем от величины -2809 Н скачок в 7298 H наверх, по-

лучаем значение -2809 + 7298 = 4489 Н. Это значение сохраня-

ется (эпюра параллельна оси) до точки 4.

В точке 4 на вал действует сила R

= 4489 H, направлен-

ная вниз. Из существующей силы в 4489 Н отнимаем 4489 H,

получаем ноль. Строим скачок до нуля.

Таким образом, к концу балки эпюра пришла в ноль. Это

признак того, что эпюра построена правильно.

Окончательно заштриховываем эпюру, отмечаем на ней

знаки сил на участках, подписываем ее «ЭF

» (т.е. «эпюра сил

по оси OX»).

3). Строим эпюру моментов по оси OX. Как указывалось

выше, на вал действуют только сосредоточенные силы. Следо-

вательно, правила (3), (5) и (6) к данной балке не относятся. При

построении эпюры моментов не усчитываем также правила (1) b

(2): (1) – поскольку оно относится к силам, а (2) – поскольку со-

средоточенных моментов на балке нет.

Согласно правилу (4), эпюра моментов на каждом участке

будет представлять собой наклонную прямую. Изменение эпю-

ры изгибающих моментов на участке будем находить по прави-

лу (7), согласно которому оно равно площади под эпюрой попе-

речных сил на этом же участке (с учетом знака).

В точке 1 на вал не действуют никакие сосредоточенные

моменты, поэтому величина момента в этой точке будет равна 0.

На участке 1-2 момент равномерно увеличивается (эпюра

представляет собой наклонную прямую), а величина изменения

равна площади под эпюрой поперечных сил: ΔМ

И(1-2)

= S

ЭQ(1-2)

τ1

· a = 9555 · 0,1 = 955 Н·м

. Строим это значение к конце уча-

стка и соединяем начало и конец прямой линией.

На участке 2-3Л эпюра также представляет собой наклон-

ную прямую. Величина изменения момента равна площади под

эпюрой поперечных сил: ΔМ

И(2-3Л)

= S

ЭQ(2-3Л)

= -10107 · 0,2 =

= -2021 Н·м. Если в начале участка величина момента была рав-

на 955 Н·м, то к концу станет равна 955 - 2021 = -1066 Н·м.

Строим это значение в точке 3Л и соединяем начало и конец

прямой линией.

На участке 3Л-3П изменение момента равно ΔМ

И(3Л-3П)

ЭQ(3Л-3П)

= -2809 · 0,1 = -281 Н·м. В начале участка величина

момента была равна -1066 Н·м, к концу станет равна -1066 - 281

= -1347 Н·м. Строим это значение в точке 3П и соединяем нача-

ло и конец прямой линией.

Наконец, на участке 3П-4 изменение момента равно

ΔМ

И(3П-4)

= S

ЭQ(3П-4)

= 4489 · 0,3 = -1347 Н·м. В начале участка

величина момента была равна -1347 Н·м, к концу станет равна

-1347 + 1347 = 0 Н·м. Проводим линию от величины -1347 Н·м в

точке 3П в ноль в точке 4. Как видим, к концу балки эпюра

пришла в ноль, что является признаком, что эпюра построена

правильно.

Окончательно заштриховываем эпюру, отмечаем на ней

знаки моментов на участках, подписываем ее «ЭM

» (т.е. «эпю-

ра моментов по оси OX»).

4). Эпюры сил и моментов по оси OY строим аналогично.

5). Окончательно получаем результат, представленный на

рисунке 3.

Данное значение можно заранее вычислить и указать рядом с эпюрой

поперечных сил, что и сделано в примере построения (см. рис. 3).

Рисунок 3. Схема нагружения вала и построение эпюр ВСФ

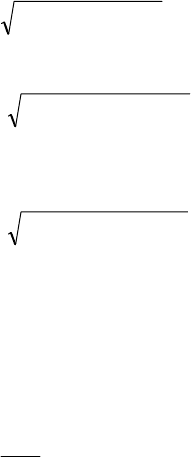
6. Определение эквивалентной нагрузки

Определяем эквивалентную нагрузку на вал. Для наиболее

нагруженных сечений вала находим эквивалентный момент. Ве-

личина эквивалентного момента (т.е. момента, учитывающего

одновременно и кручение, и изгиб по осям OX и OY) определя-

ется как:

экв

222

крYX

MMM ++

Отсюда находим эквивалентный момент. В сечении 2:

= 955 H·м; M

= 382 H·м; M

кр2

= 955 H·м

экв2

2 крYX

MMM ++ = 1403 H·м

Из двух сечений 3 выбираем правое, т.к. в нем все дейст-

вующие на вал моменты больше. Тогда:

= 1347 H·м; M

=71 H·м; M

кр3

= 477,5 H·м

экв3

3 крYX

MMM ++ = 1431 H·м

Таким образом, сечение 3П наиболее опасно, т.к. в нем на

вал действует наибольший эквивалентный момент. Данную ве-

личину момента и выбираем для дальнейших расчетов.

7. Расчет размеров вала из условия прочности

Условие прочности при сложном нагружении имеет вид

ЭКВ

[]

≤ .

Здесь σ

ЭКВ

– т.н. «эквивалентная нагрузка», учитывающая

действие одновременно нормальных и тангенциальных напря-

жений. Однако при разных условиях нагружения нормальные и

тангенциальные напряжений вносят различный вклад в разру-

шение материала. Это означает, что невозможно вывести еди-

ную формулу, учитывающую влияние сразу и нормальных, и

тангенциальных напряжений при всех случаях нагружения. По-

этому в сопротивлении материалов используются

гипотезы

прочности

, т.е. расчетные гипотезы, позволяющие установить

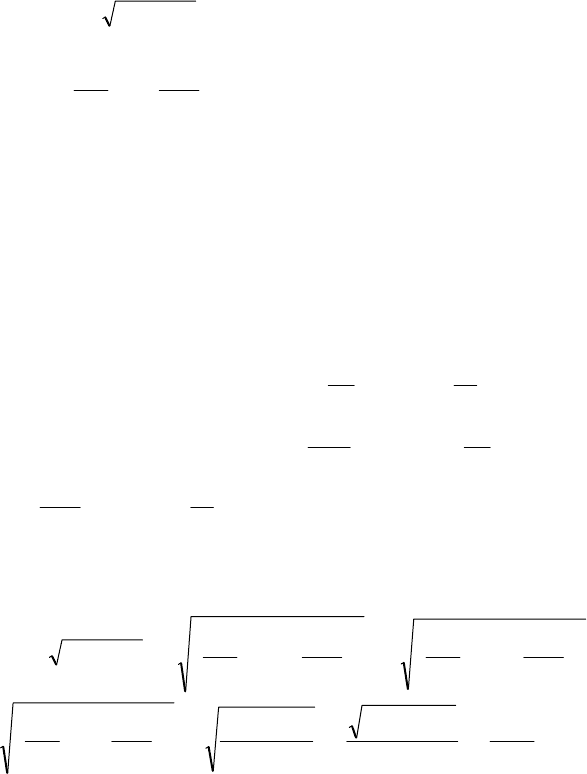
относительный вклад различных видов напряжений в разруше-

ние материала.

Одной из широко применимых является т.н. «третья гипо-

теза прочности», она же «гипотеза максимальных тангенциаль-

ных напряжений» или «гипотеза Треска – Сен-Венана» (по име-

ни предложивших ее ученых). Согласно третьей гипотезе проч-

ности, при сложном нагружении

ЭКВ

τσ

+ .

Здесь

σ =

, τ =

кр

Величины W

и W

кр

– это т.н. моменты сопротивления из-

гибу и кручению

. Они являются конструктивными параметрами

вала, учитывающими его прочность при изгибе и кручении со-

ответственно. Обращаем особое внимание, что данные парамет-

ры учитывают прочность не

материала, а формы вала, т.е. по-

казывают, насколько эффективно будет сопротивляться нагруз-

ке вал той или иной конструкции (того или иного поперечного

сечения). Моменты сопротивления изгибу измеряются в м

равны:

- для сплошного круглого вала W

, W

кр

;

- для цилиндрического вала W

D32

– d

) =

(1 – δ

кр

D16

– d

) =

(1-δ

где δ = d/D.

Видим, что в обоих случаях выполняется соотношение

кр

= 2W

, что позволяет упростить расчетную формулу:

ЭКВ

τσ

+ =

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

кр

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

кр

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

кр

кри

ММ +

кри

ММ

экв

Таким образом, напряжения при сложном нагружении ва-

ла одновременно изгибающим и крутящим моментами можно

определить как

ЭКВ

экв

что дает вид условия прочности

экв

[]

≤ .

Это основное уравнение конструктивного или провероч-

ного расчета вала, из которого можно определить любой крите-

рий, зная остальные. В нашем случае известны:

- эквивалентный момент нагрузки М

экв

– определен выше,

см. п. 6;

- коэффициент запаса прочности k – дан по условию рас-

четно-графической (контрольной) работы, k = 3 для всех вари-

антов;

- предел текучести материала [σ

], который находим по

справочной таблице, например в учебнике [4]. Согласно усло-

вию, материал вала – Сталь 3 (Ст.3), откуда предел текучести

[σ

] = 220 МПа = 220·10

Па.

Необходимо определить диаметр вала, который может

быть выражен из конструктивного параметра W

. Сначала нахо-

дим необходимый момент сопротивления изгибу:

[]

экв

kМ

⋅

, что в нашем случае дает W

10220

31431

⋅

19,51·10

-6

(м

Находим диаметр вала. Для круглого вала сплошного по-

перечного сечения необходимый диаметр равен:

круг

1051,1932

−

⋅⋅

= 58,36·10

-3

(м) = 58,36 (мм).

Для вала цилиндрического сечения необходимый диаметр

равен:

цил

)1(

δπ

−

В нашем случае δ = 0,9, откуда

цил

)9,01(

1051,1932

−

⋅⋅

−

= 83,29·10

-3

(м) = 83,29 (мм).

Видим, что D

круг

< D

цил

, т.е. с точки зрения габаритов вал

сплошного сечения лучше цилиндрического, так как он более

компактный. Однако это не говорит о выигрыше в расходе ме-

талла. Не забудем, что цилиндрический вал имеет довольно тон-

кую стенку, т.к. внутренний диаметр, по условию, равен 0,9 от

внешнего (d = 0,9D). Поэтому чтобы оценить расход материала

на изготовление того и другого вала, необходимо провести до-

полнительный расчет.

Чтобы сравнить расход металла на изготовление валов,

можно сравнить их погонные веса. Погонный вес – это вес про-

филя длиной 1 м без учета его конфигурации. Однако если мы

примем несколько профилей длиной по 1 м каждый, и при этом

изготовленных из одного и того же металла, то погонные веса

будут соотносится так же, как площади поперечного сечения

профилей. Таким образом, сравним площади поперечного сече-

ния найденных нами валов.

Площадь вала сплошного круглого сечения (площадь кру-

га):

кр

= πR

= πD

/4.

В нашем случае

кр

круг

36,58

⋅

= 2675 (мм

) = 26,75 (см

Площадь вала цилиндрического сечения (площадь коль-

ца):

кол

= πR

- πr

ππ

− = )1(

−

В нашем случае

кол

= )1(

−

цил

= )9,01(

29,83

−

⋅

= 1035 (мм

) =

10,35 (см

Таким образом, соотношение габаритных размеров валов

составляет D

круг

/ D

цил

= 58,36 / 83,29 = 0,7, а соотношение их

площадей составляет S

кр

/ S

кол

= 26,75 / 10,35 = 2,58. То есть, хо-

тя внешний диаметр цилиндрического вала примерно в полтора

раза больше, чем у круглого, но на его изготовление требуется

примерно в два с половиной раза меньше металла.

8. Ответ

Необходимый диаметр вала сплошного круглого сечения

из условия прочности D = 58,36 мм, вала цилиндрического сече-

ния D = 83,29 мм. Соотношение расхода металла на изготовле-

ние данных валов (или их погонных весов) составляет 2,58 в

пользу вала кольцевого сечения.

Литература

1. Скрягин В.В., Соловьева Л.В. Сопротивление материа-

лов. – Петропавловск-Камчатский: КамчатГТУ, 2002. – 62 с.

2. Тарг С.М. Краткий курс теоретической механики:

Учебник. 12 изд., стер. – М.: Высшая школа, 2001.

3. Феодосьев В.И. Сопротивление материалов: Учеб. для

вузов. – 11-е изд., стереотип. – М.: Изд-во МГТУ им

Н.Э.Баумана, 2003. – 592 с.

4. Эрдеди А.А., Эрдеди Н.А. Теоретическая механика. Со-

противление материалов: 4-е изд., перераб. и доп. – М.: Высшая

школа, 2002. – 318 с.

Примечание. Допускается использовать другие издания

данных учебников, а также другие учебники по предмету «Тех-

ническая механика».