Лупанов О.Б. Лекции по математической логике
Подождите немного. Документ загружается.


Функцию min(x
1
, x
2
) выразим так: min(x
1
, x
2
) = N
max (N(x
1
), N(x
2
))
, применив аналог правила Де Мор-
гана x
1
x
2
= x
1
∨ x
2
. Покажем, как получить любую функцию одной переменной. Построим функции вида
ϕ
α,β
(x) :=
(
β, x = α
0, x 6= α.
Такие функции можно выразить формулой ϕ
α,β
(x) = max(J
α
(x), k − (β + 1)) + β + 1. Тогда любая функция
ψ(x) ∈ P
k
(1) выражается формулой ψ(x) = max(ϕ
0,ψ(0)
, ϕ
1,ψ(1)
, . . . , ϕ
k−1,ψ(k−1)
). Таким образом мы можем
получить N(x). Следовательно, наша система полная.
Утверждение 2.4. Система {V (x) := max(x
1
, x
2
) + 1} — полная.
Функция V (x) является аналогом штриха Шеффера и называется функцией Вебба. В самом деле,
V (x, x) = x + 1 ⇒ можно получить функцию вида x + c. Возьмем c = k − 1. Тогда V (x
1
, x
2
) + k − 1 = max(x
1
, x
2
),
а полученные функции образ уют базис P
k
.
Теорема 2.5. Дл я любого k в P
k
существует конечное число пре дполных классов A
1
, . . . A
q
. [F] = P
k
⇔
⇔ F * A
i
∀ i = 1, q. Доказательства этой те оремы в на шем курсе не будет.
Пусть π(k) — количество предполных классов в P
k
. Вот их количество при разных k:
k 2 3 4 5 6
π(k) 5 18 80 6 67 15237
Справедлива асимптотическая формула:
π(k) ⋍ δ(k) · k · 2
C
m
k−1
, m =
k − 1
2
, δ(k) =
(
1, k ≡ 1 (mod 2);
2, k ≡ 0 (mod 2).
Рассмотрим алгоритм распознавания полноты в P
k
. Пусть F = {f
1
(x
1
, . . . , x
n
1
), . . . , f
s
(x
1
, . . . , x
n
s
), . . . }. Возь-
мём переменные x
1
и x
2
и построим последовательность множеств Π
i
по следующему правилу: Π
1
= ∅; Π
i+1
=
= Π
i
∪
f
j
(A
1
, . . . , A
n
j
)
, где A
k
∈ {x
1
, x
2
} ∪ Π
i
. Тогда Π
1
⊆ Π
2
⊆ Π
3
⊆ · · · ⊆ P
k
(2), но так как |P
k
(2)| < ∞, то
начиная с некоторого момента Π
t
= Π
t+1
= Π
t+2
= . . . . Очевидно, что [F] = P
k
⇔ V (x
1
, x
2
) ∈ Π
t
.
2.3. Критерии полноты в P
k
. Теорема Слупецкого – Яблонского
Определение. f(x
1
, . . . , x
n
) ∈ P
k
(n) — существенная функция, если она зависит не менее, чем от 2 пере-
менных и принимает k значений.
Теорема 2.6 (Слупецкого – Яблонского). Пусть F ⊇ P
k
(1). [F] = P
k
⇔ F содержит существенную
функцию. Усиление С. В. Яблонского: тот же самый вывод исходя из предположения о том, что F содержит
все функции одной переменной, принимающие не более k − 1 значения.
⇒ Будет доказано для случая Слупецкого. Предположим, что F содержит все функции от одной пе-
ременной и ни одной су щ ественной. Тогда покажем, что F неполная. В самом деле, любая формула над F
имеет вид f
i
1
(f
i
2
(. . . f
i
l
(g(x
l
1
, x
l
2
, . . . )) . . . )), где f
i
j
∈ P
k
(1), а g — самая внешняя в этой формуле среди всех
функций б олее чем одной переменной. Но g не является существенной функцией по предположению, значит,
она принимает не более k − 1 значения. Но тогда и вся формула не может принимать больше k − 1 значения,
следовате льно, любая функция над F принимает не более k − 1 значения. Значит, F — неполная.
⇐ Докажем для случая Яблонского, а значит и для случая Слупецкого. Пусть k > 3. Нам понадобится
Лемма 2.7 (о трёх наборах). П усть f ∈ P
k
(n) существе нно зависит не менее, чем от 2 переменных и
принимает не менее 3 значений. Тогда существуют 3 набора
A = (α, α
2
, . . . , α
n
),
B = (β, α
2
, . . . , α
n
),
C = (α, δ
2
, . . . , δ
n
),
такие, что f(A) 6= f (B) 6= f (C).
Для определенности будем считать, чт о f существенно зависит от переменной x
1
. Следовательно, на й-
дутся наб оры eα = (α, α
2
, . . . , α
n
) и
e
β = (β, α
2
, . . . , α
n
), такие что f(eα) = ε
1
, f(
e
β) = ε
2
, причём ε
1
6= ε
2
. Рассмотрим
множество наборов M = {(0, α
2
, . . . , α
n
), (1, α
2
, . . . , α
n
), . . . , (k − 1, α
2
, . . . , α
n
)}. В озможны 2 случая:
1
◦
Если среди f(M) имеется только 2 различных з начения, то по условию существует набор
e
δ = (δ, δ
2
, . . . , δ
n
),
такой, что f(
e
δ) 6= ε
1
, f(
e
δ) 6= ε
2
. Тогда (δ, α
2
, . . . , α
n
) ∈ M, и f(δ, α
2
, . . . , α
n
) ∈ {ε
1
, ε
2
}. Пусть, для определенности,
11
f(δ, α
2
, . . . , α
n
) = ε
1
. Тогда найдётся γ, такое что f(γ, α
2
, . . . , α
n
) = ε
2
. Таким образом, искомые наб оры —
(δ, α
2
, . . . , α
n
),
(γ, α
2
, . . . , α
n
),
(δ, δ
2
, . . . , δ
n
).
2
◦
Среди f(M) имеется не менее 3 различных значений. Среди функций
f(0, x
2
, . . . , x
n
), . . . , f(k − 1, x
2
, . . . , x
n
)
хотя бы одна — не константа, поскольку f существенно зависит не только от x
1
. Пусть f(α, x
2
, . . . , x
n
) — не
константа. Тогда найдётся набор (δ
2
, . . . , δ
n
), такой, что ε
1
= f (α, δ
2
, . . . , δ
n
) 6= f (α, α
2
, . . . , α
n
) = ε
2
, но в силу
существенной зависимости от x
1
существует β : f(β, α
2
, . . . , α
n
) = ε
3
.
Определение. Квадрат — это четыре набора вида
(α
1
, . . . , α
i−1
, α, α
i+1
, . . . , α
j−1
, β, α
j+1
, . . . , α
n
),
(α
1
, . . . , α
i−1
, γ, α
i+1
, . . . , α
j−1
, β, α
j+1
, . . . , α
n
),
(α
1
, . . . , α
i−1
, α, α
i+1
, . . . , α
j−1
, δ, α
j+1
, . . . , α
n
),
(α
1
, . . . , α
i−1
, γ, α
i+1
, . . . , α
j−1
, δ, α
j+1
, . . . , α
n
),
где α 6= γ, β 6= δ.
Лемма 2.8 (о квадрате). П усть f существенно зависит не менее, чем от 2 переменных, и принимает
не менее 3 значений. Тогда существует квадрат, на котором одно значение п ринимается ровно 1 раз.
По лемме о трёх наборах существуют наборы
eσ
1
= (α
1
, α
2
, . . . , α
n
), f(eσ
1
) = ε
1
,
eσ
2
= (δ
1
, α
2
, . . . , α
n
), f(eσ
2
) = ε
2
,
eσ
3
= (δ
1
, δ
2
, . . . , δ
n
), f(eσ
3
) = ε
3
,
причем ε
1
6= ε
2
6= ε
3
. Построим цепочку квадратов
α
1
α
2
α
3
α
4
. . . α
n
δ
1
α
2
α
3
α
4
. . . α
n
α
1
δ
2
α
3
α
4
. . . α
n
δ
1
δ
2
α
3
α
4
. . . α
n
α
1
δ
2
δ
3
α
4
. . . α
n
δ
1
δ
2
δ
3
α
4
. . . α
n
. . . . . . . . . . . . . . . . . .
δ
1
δ
2
δ
3
δ
4
. . . δ
n
Здесь первый квадрат — это строки [1 . . . 4], вто рой — [3 . . . 6], третий — [5 . . . 8], и т. д. На первых двух наборах
значения функции равны соответственно ε
1
и ε
2
, а на последнем — ε
3
. З начит, рано или поздно в по с ледова-
тельности квадратов появится квадрат, на котором одно из значений ε
1
, ε
2
, ε
3
принимается ровно 1 раз.
Приступим к доказательству основной теоремы. Сначала пос троим все функции, принимающие ровно 2
значения, а затем по индукции из всех функций, принимающих не более l значений, получим все функции, при-
нимающие l + 1 значение. По условию, у нас есть существенная функция f. Поскольку k > 3, она удовлетворяет
условиям леммы о квадрате. Рассмотрим наборы, образ ующие квадрат, на котором како е -то значение, скажем,
ε
1
, принимается ровно 1 раз, т. е. ε
1
/∈ {ε
2
, ε
3
, ε
4
}:
f(α β α
3
. . . α
n
) = ε
1
f(γ β α
3
. . . α
n
) = ε
2
f(α δ α
3
. . . α
n
) = ε
3
f(γ δ α
3
. . . α
n
) = ε
4
Введем обозначение ϕ(x
1
, x
2
) := f (x
1
, x
2
, α
3
, . . . , α
n
). Теперь рассмотрим функции:
ψ(x) :=
(
0, x = ε
1
1; x 6= ε
1
,
λ
1
(x) :=
(
α, x = 0;
γ, x 6= 0,
λ
2
(x) :=
(
β, x = 0;
δ, x 6= 0 ,
ω(x
1
, x
2
) := ψ
ϕ
λ
1
(x
1
), λ
2
(x
2
)
.
Все эти функции у на с есть, поскольку они принимают не более 2 (а значит, и не более k − 1) значений.
Заметим, что на наборах из нулей и единиц функция ω ведёт себя так же, как обычная дизъюнкция, поэтому
12

обозначим е ё через
e
W
(x
1
, x
2
). Кроме того, у нас есть фу нкция j
α
(x) :=
(
1, x = α
0, x 6= α,
так как она принимает
только 2 значения. Построим функцию
e
&(x
1
, x
2
) := j
0
ω
j
0
(x), j
0
(x
2
)
, которая на наборах из нулей и единиц
ведет себя как обычная конъюнкция. Функции
e
W
и
e
& позволяют соорудить аналог СДНФ и получит ь все
функции, которые на наборах из 0 и 1 принимают значения 0 и 1, т. е. все фу нкции из P
2
⊂ P
k
. Теперь с
помощью этих функций получим функцию, которая принимает любые 2 значения (а не только 0 и 1). Пусть
h(x
1
, . . . , x
m
) принимает только значения α и β. По условию у нас есть µ(x) :=
(
α, x = 0;
β, x 6= 0.
Но у нас есть
и g(x
1
, . . . , x
m
) :=
(
0, h(x
1
, . . . , x
m
) = α;
1, h(x
1
, . . . , x
m
) = β,
тогда h(x
1
, . . . , x
m
) = µ
g(x
1
, . . . , x
m
)
. Таким образом, мы умеем
делать функции, принимающие любые 2 значения.
Теперь из функций, принимающих не более l − 1 значения, получим функции, принимающие l значений.
Пусть g(x
1
, . . . , x
m
) принимает значения {ε
1
, . . . , ε
l
}. Из леммы о трех наборах следует существование такой
совокупности наборов, что
f(α α
2
. . . α
n
) = ε
1
f(β α
2
. . . α
n
) = ε
2
f(α δ
2
. . . δ
n
) = ε
3
f(β
41
β
42
. . . β
4n
) = ε
4
. . .
f(β
l1
β
l2
. . . β
ln
) = ε
l
(1)
В каждом столбце этой матрицы наборов стоит не более l − 1 различных значений. Значения ε
1
, ε
2
, ε
3
фигу-
рируют в лемме о трех наборах и все различны. Функция f — существе нная и потому принимает k значений.
Следовательно, значения ε
4
, . . . , ε
l
мы можем выбрать так, чт обы все ε
i
были различны. Покажем, как можно по-
лучить про извольную функцию, принимающую эти же l значений. Нам ну жно получить функцию g(x
1
, . . . , x
m
)
такую, что Im g ⊆ {ε
1
, . . . , ε
l
}. Каждому наб ору eσ = (σ
1
, . . . , σ
m
) сопоставим число (индекс) i(eσ) ∈ {1, 2 , . . . , l} :
g(eσ) = ε
i(eσ)
. Построим n функций h
j
(eσ) : h
j
(x
1
, . . . , x
m
) = β
i(eσ)j
, где элемент β
ij
соотв е тствует ij-тому элементу
приведённой выше ма трицы наборов . Функции h
j
у нас ест ь по предположению индукции, т.к. принимают не
более l − 1 значения. Тогда функция g выражается формулой g = f(h
1
, . . . , h
n
) = f
β
i(eσ)1
, . . . , β
i(eσ)n
. Та ким
образом, мы можем полу чить любую функцию, принимающую значения {ε
1
, . . . , ε
l
}, и шаг индукции доказан.
Завершим доказательство теоремы построением произвольной функции g, принимающей люб ы е l значений
{ξ
1
, . . . , ξ
l
}. Рассмотрим функцию θ(x) : θ(ε
i
) = ξ
i
. Чтобы θ принимала не более l различных значений, положим
θ(x) = ξ
1
, x /∈ {ε
1
, . . . , ε
l
}. Так можно сделать, поскольку значения функции θ не на ε
i
нас не интересуют. У нас
уже есть функция h : h(eσ) = ε
i
, если g(eσ) = ξ
i
. Тогда функция g выражается так: g = θ(h).
Определение. Функция f назыв ается ш ефферовой, если
{f}
= P
k
.
Теорема 2.9. f — шефферова ⇔ f порождает все функции из P
k
(1), принима ющие не более k −1 значения.
⇒ Тривиально: эта функция порождает все функции.
⇐ Покажем, что эта функция существенна. Обо значим E := {0, 1, . . . , k − 1}. Если Im f 6= E, то из нее
нельзя получить функцию, принимающую отсутствующее значение, а среди функций от одной переменной такая
обязательно найдется. Значит, f должна принимать все k значений. Если она су щ ественно зависит только от
одной переменной, то, следовательно, является перестановкой, а композиция перестановок — тоже перестановка,
значит, константу из неё получить нельзя. Значит, она сущ ественно зависит не менее чем от 2 переменных, и
по определению существе нна. По теореме Я блонского
{f}
= P
k
.
Далее речь пойдет об алгебраической с истеме функций в P
k
. Сложение и умножение, естестве нно, подразу-
меваются по модулю k.
Утверждение 2.10. Система E ∪ {× +} полная ⇔ k — простое число.
Пусть k — простое число. Положим ϕ(x) := 1−x
k−1
. Имеем ϕ(0) = 1, а по малой теореме Ферма ϕ(a) ≡ 0
(mod k), если a 6= 0. Следовательно , ϕ = j
0
. Легко видеть, что j
α
(x) = j
0
(x− α). Но так как для любой функции
f мы имеем полиномиальное выражение над E ∪ {× + j
0
(x), . . . , j
k−1
(x)} вида
f(x
1
, . . . , x
n
) =
X
(σ
1
,...,σ
n
)
j
σ
1
(x
1
) × · · · × j
σ
n
(x
n
) × f(σ
1
, . . . , σ
n
),
то система полная.
Предположим теперь, чт о k — составное число, т. е. k = mn и m, n > 1, и докажем, что наша система
неполная. Покажем, что j
0
(x) не представляется в виде полинома j
0
(x) = c
0
+ c
1
x + c
2
x
2
+ · · · + c
p
x
p
. Т.к.
j
0
(0) = 1, то c
0
= 1. Но в силу того, что m 6= 0, имеем 0 = j
0
(m) = 1 + c
1
m + · · · + c
p
m
p
. Домножим это
13
равенство на n, тогда почти все с лагаемые поубиваются (mn ≡ 0 (mod k)), и останется неверное равенство
0 = n. Противоречие.
2.4. Замкнутый класс без базиса
Утверждение 2.11. Если k > 3, то в P
k
существует замкнутый класс, не имеющий базиса.
Рас с мотрим класс функций вида ϕ
i
(x
1
, . . . , x
i
), равных 1 на наборах из одних двоек, и 0 в противном
случае. Он, очевидно, замкнут, поскольку при подстановке функции ϕ
i
в функцию ϕ
j
мы получаем нуль. Дей-
ствительно, функция ϕ
i
никогда не принимает значение 2, стало быть, аргументы ϕ
j
— не есть набор сплошь
из двоек. От с юда следует, что из функции с меньшим номером нельзя получить функцию с большим номером.
Значит, с одной стороны, базис должен содержать все функции ϕ
i
, а с другой стороны, отождествлением пе-
ременных можно из функции с большим номером получить все функции с меньшими номерами. Значит, этот
класс баз иса не имеет.
2.5. Класс, имеющий счётный базис
Рассмотрим множество функций вида ψ
i
(x
1
, . . . , x
i
), равных 1, если среди аргументов ровно 1 единица, а
остальные — двойки, и равных 0 во всех остальных случаях. Оно, очевидно, замкнуто.
Утверждение 2.12. Любая из функций ψ
i
не выражается через остальные.
Докажем, что ψ
i
не может получиться из ψ
j
путём отождествления переменных. В самом деле, положим
отождествлённую переменную равной 1, остальные — 2. Тогда функция с меньшим число м переменных будет
равна 1, а другая — 0, т.к. среди её аргументов более одной единицы. Теперь докажем, что одна функция
не получается из другой при помощи подстановки. Рассмотрим два случая. 1
◦
Среди аргументов функции ψ
i
есть ровно 1 подформула на s-м месте. Тогда подставим наб ор с единицей на люб ом месте, кроме s-го. Тогда
функция с подформулой примет значение 0 (аналогично случаю отождествления), а без подформулы — 1.
Значит, эти две функции не равны. 2
◦
Среди аргументов есть хотя бы 2 подформулы. Подставим любой набо р
вида (2, . . . , 2, 1, 2, . . . , 2). Очевидно, функция с подформулами на нём обнулится, а без подформул — нет.
Отсюда следует, что любое подмножество данного класса замкнуто, и каждая функция, в свою очередь,
является базисной. Значит, в P
k
континуум замкнутых классов, ибо их столько же, сколько бесконечных после-
довательностей из нулей и единиц. Действительно, можно установить биекцию между любым подмножеством
этого класса и множеством последовательностей: на i-том месте в последов ательности ставим 0, если ψ
i
не
лежит в данном подмножестве, и 1 в противном случае. Каждая последовательно с ть — бесконечная двоичная
дробь без разделительной то чки. Значит, классов столько же, сколько и всех дейст вительных чисел.
3. Схемы из функциональных элементов
3.1. Графы
Определение. Граф — это упорядоченная пара (V, E), где V — не более чем счётное множество, элементы
которого называются вершинами, а E ⊆ V × V — множество пар вершин {(v
i
, v
j
)}, называемых рёбрами графа.
Концами реб ра называются элементы пары, образу ющей ребро. Если концы совпадают, то ребро называется
петлёй. Вершина называется изолированной, если она не являет ся концом никакого ребра. Вершина называется
концевой, если она является концом ровно одного ребра.
Определение. Подграф графа (V, E) — такой гра ф (W, F ), что W ⊆ V и F ⊆ W × W .
Определение. Геометрическая реализация графа. Рассмотрим R
n
. Отметим в нём с только точек, сколько
вершин у нашего графа. Каждому ребру поставим в соответствие кривую, соединяющую концы этого ребра.
Эту кривую мы тоже будем называть ребро м. То, что получится, и будет геометрической реализацией. Геомет-
рическая реализация называется правильной, если у рёбер нет общих т очек, кроме, быть может, вершин.
Утверждение 3.1. В R
3
для любого графа имеется правильная геометрическая реализация.
Сперва расставим вершины произвольно. Очевидно, путём малых шевелений можно сделать так, что
никакие 4 не будут лежать в одной плоскости. Теперь для любых трёх вершин есть с воя плоскость, а плоский
граф из трёх вершин, очев идно, допускает правильную реализацию.
Определение. Путь — конечная последовательность рёбер графа (v
i
1
, v
i
2
), (v
i
2
, v
i
3
), . . . , (v
i
n−1
, v
i
n
). Говорят,
что путь соединяет вершины v
i
1
и v
i
n
. Простой пут ь (цепь) — путь, все вершины которого различны. Цикл —
путь, у которого v
i
1
= v
i
n
. П ростой цикл — цикл, у которого все рёбра и все вершины, кроме концов, различны.
Граф называется связным, если любые 2 его вершины можно соединить путём. Дере вом наз ывается связный
граф без простых циклов.
14
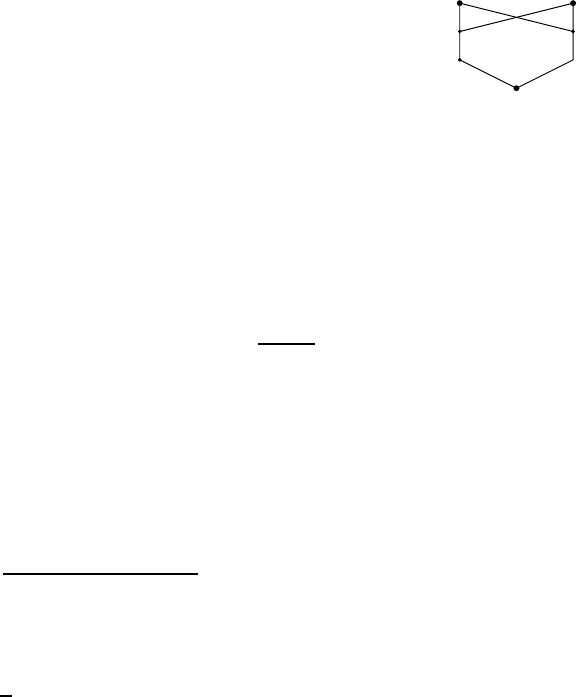
Утверждение 3.2. Из каждого конечного св язного графа можно выделить подграф, содержащий все вер-
шины исходного графа и являющийся деревом.
Если в графе есть простой цикл, то можно убрать из цикла одно ребро, не нарушив связности. Будем
убирать рёбра, пока простых циклов не станет.
Определение. Назовё м граф ориентированным, если каждому его ребру приписано направление.
Определение. Ориентированн ый цикл — цикл, в котором все рёбра направлены в одну сторону, т. е. ко-
нечная последовательность о риентированных рёбер
−−−−→
v
i
, v
i+1
, где первая вершина совпадает с последней.
Лемма 3.3. В любом конечном ориентированном графе без ориентированных циклов есть в ершина, из
которой рёбра не выходят.
От противного: выберем любую вершину и, исходя из неё, будем двигаться по рёбрам в напра влении,
приписанном данному ребру. Если из каждой вершины выходит хотя бы одно ребро, то рано или поздно мы
вернёмся туда, где уже были, поскольку граф конечен. Но это будет ориентированный цикл. Противоречие.
Теорема 3.4. В любом конеч ном ориентированном графе без ориенти рованных циклов можно зануме-
ровать вершины первым и натуральными числами так, что каждое ребро будет направлено от вершины с
меньшим номером в вершину с большим номером.
Докажем индукцией по числу вершин p. При p = 1 утв е рждение очевидно. Пусть p > 1. Предположим,
что это верно для всех графо в с числом вершин, меньшим p. Рассмотрим граф с p вершинами. По лемме у него
есть вершина, из которой рёбра не выходят. Уберём из графа эту вершину и в с е входящие в неё рёб ра, получим
граф с числом вершин, меньшим p. По предположению индукции такой граф допускает искомую нумерацию
вершин числами 1, 2, . . . , p − 1. Тогда присвоим выкинутой вершине номер p.
3.2. Схемы из функциональных элементов
&
6 ∗
5
¬
3
&
1
x
1
2
x
2
4
∨
Определение. Схема из функциональных элементов (СФЭ) — это конечный ориентиро-
ванный граф без ориентированных циклов, в каждую вершину которог о входит не более 2
рёбер. При этом каждой вершине приписывается с имвол: переменная x
i
, если в э ту вершину
рёбра не входят; отрицание, если в вершину входит одно ребро; конъюнкция или дизъюнкция,
если в вершину входит 2 ребра. Некоторым вершинам приписывается ∗. Элементами схемы
называются вершины, помеченные логическими операциями.
Занумеруем вершины графа согласно предыдущей теореме. Каждой вершине СФЭ можно сопоставить неко-
торую булеву функцию по следующему индуктивному правилу. Пусть всем вершинам с номерами меньше n уже
сопоставлены функции. Возьмём ве ршину с номером n. Если в неё не входит ни одного ребра, то ей приписана
переменная, которую мы как функцию и поставим ей в соответствие. Если в вершину входит одно ребро, то
в ней записано отрицание, и мы припишем этой вершине отрицание функции той вершины, из которой в да н-
ную вершину приходит ребро. Если входит два ребра, то в этой вершине будет конъюнкция или дизъюнкция
функций тех вершин, из которых приходят эти рёб ра. Видно, что такое определение корректно.
Определение. Функции, отвечающие вершинам, отмеченным ∗, назы ваются реализуемыми данной СФЭ.
Пример 2.1. Приведённая выше схема реализует функцию (x
1
∨ x
2
)&(x
1
&x
2
) = x
1
⊕ x
2
.
Существует физическая интерпретация СФЭ, в которой они ра ссматриваются как математические модели
соотв е тствующих реальных элект ронных схем: если на вход подаётся набор значений (наличие тока соотв е т-
ствует единице, отсу тствие — нулю), то на выходе получается значение функции на этом наборе.
Определение. Сл ожностью схемы S называется число элементов L(S) в ней. Сложностью функции f
называет ся минимальная сложность схемы для f. Функция Шеннона L(n) выражает максимальную сложность
функций от n переменных.
Построим СФЭ, реализующу ю функцию f = x
σ
1
1
. . . x
σ
n
n
. Перег ру ппируем множители, соб рав в одном месте
переменные с нулевыми степенями. Тогда, перенумеровав переменные и применив правило Де Моргана, функ-
цию можно переписать в виде f = (x
1
x
2
. . . x
k
)(x
k+1
∨ x
k+2
∨ · · · ∨ x
n
). Заметим, что в э той формуле не более n
операций. Значит, сложность схемы данной функции не превосходит n. Теперь пос троить схему легко.
Теперь мы сможем ограничить сложность любой функции f све рху. По с троим СДНФ для этой функции. В
ней может быть не более 2
n
дизъюнкций выра жений вида x
σ
1
1
. . . x
σ
n
n
. Так как сложность каждого дизъюнкта
мы уже оценили числом n, то сложность всей схемы не превосходит n · 2
n
. Для функций, тождественно равных
нулю, можно использоват ь формулу f = x
1
&x
1
. При этом мы предполагаем, что f — функция по крайней
мере от одной переменной. Схема будет содержат ь 2 элемента, значит, её сложность L(f ) = 2 6 n · 2
n
. Итак,
сложность любой функции L(n) 6 n · 2
n
.
Замечание. На самом деле можно сэкономить ещё в 2 раза. Действительно, если среди значений функ-
ции по всем наборам больше нулей, чем единиц, то выгодно использовать СДНФ, а если наоборот, то СКНФ
15
(конъюнктивную форму, т. е. конъюнкцию дизъюнкций).
3.3. Контактные схемы
Определение. Контактная схема (КС) — эт о конечный граф, в котором каждому ребру приписана пе-
ременная либо её отрицание и отмечены некоторые вершины — полюса. Ф ункция проводимости полюсов a и
b некоторой контактной схемы — функция f
a,b
, которая равна 1, если a = b; равна 0, если в КС нет цепей,
соединяющих a и b; в остальных случаях f равна дизъюнкции всех цепей, соединяющих a и b, а каждая цепь
равна конъюнкции всех своих рёбе р. Сложностью КС называют число рёбер в ней.
a
b
x
1
x
2
x
2
x
3
x
1
x
2
x
3
x
2
Пример 3.1. Здесь f
a,b
= x
1
x
2
x
3
∨ x
1
x
2
x
3
∨ x
1
x
2
x
3
∨ x
1
x
2
x
3
= x
1
⊕ x
2
⊕ x
3
.
Остальные цепи, соединяющие a и b, равны нулю, поскольку содержат какую-
нибудь переменную вместе с её отрицанием.
Если граф неориентированный, то f
a,b
= f
b,a
.
Для каждой контактной схемы составим матрицу функции проводимости, в
которую поместим значения функции проводимости на всевозможных полюсах.
В примере, приведённом выш е , эта мат рица выглядела так:
a b
a 1 x
1
⊕ x
2
⊕ x
3
b x
1
⊕ x
2
⊕ x
3
1
Пусть число полюсов равно k. Выясним, какие условия надо наложить на произвольную матрицу k × k,
состоящую из функций, чтобы существовала КС с такой матрицей проводимости. Для любых трёх полюсов i, j, k
необходимо, чтобы f
i,k
принимала значение 1 на всех наборах, на которых f
i,j
и f
j,k
одновременно принимают
значение 1. Это означает, что f
i,k
> f
i,j
f
j,k
. Для неориентированных КС матрица должна быть симметрична
относительно главной диагонали. На диаго нали матрицы должны стоять единицы (по определению функции
проводимости). Можно доказать, что этих трёх требований достаточно для суще ствования КС с такой матрицей
проводимости.
a
b
a
12
1
a
13
2
a
14
3
a
1n
n
a
21
1
a
22
2
a
23
3
a
2n
n
a
s1
1
a
s2
2
a
s3
3
a
sn
n
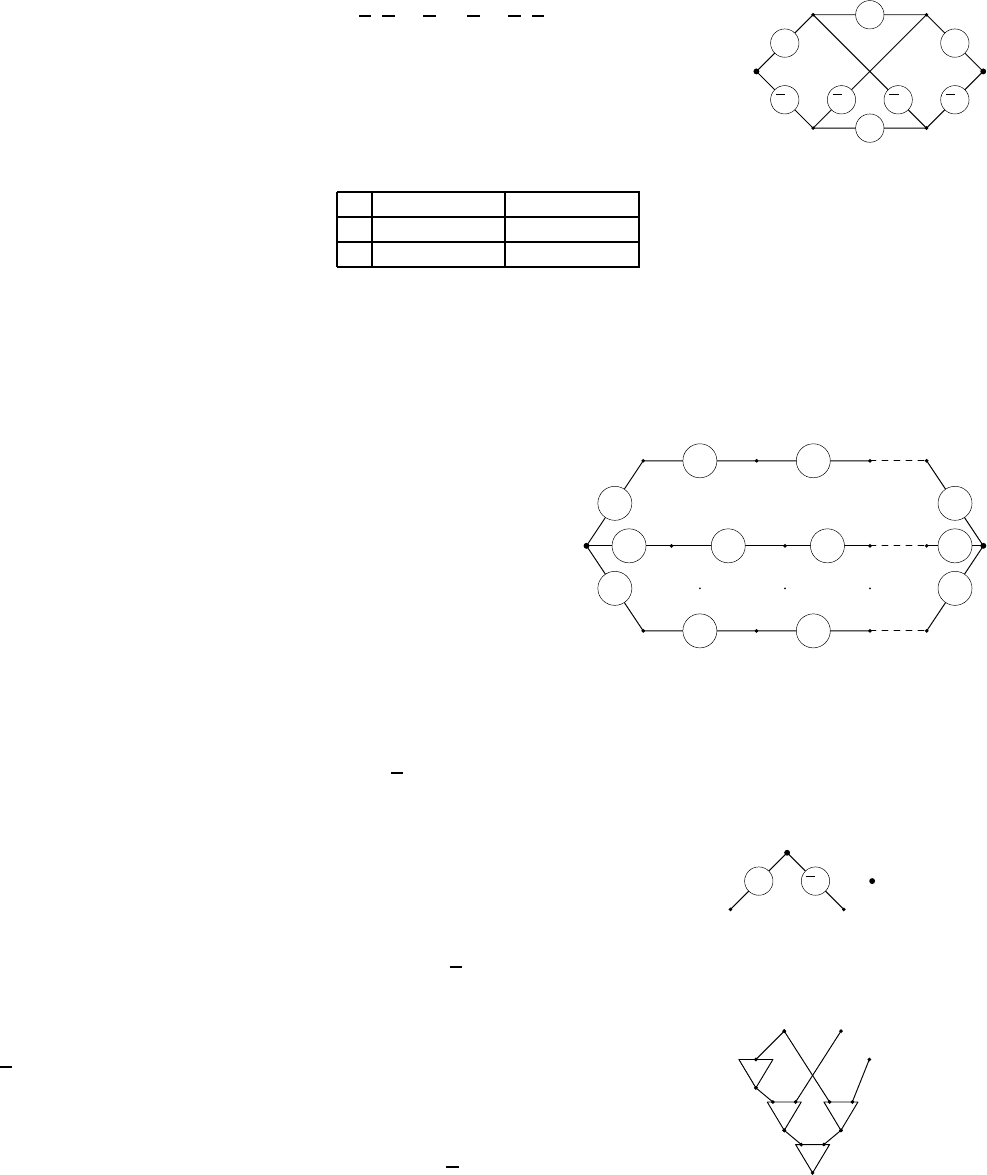
Оценим сверху сложность функции f от n переменных. Вос-
пользуемся правилом построения СДНФ: выберем все наборы
(σ
1
, . . . , σ
n
), на которых функция равна 1 . Их число s не пре-
восходит 2
n
. Для каждого набора построим цепь, соединяющую
два по люса схемы и реализующую фу нкцию x
σ
1
1
. . . x
σ
n
n
(на ри-
сунке a
ij
k
:= x
σ
ij
k
). В каждой такой цепи ровно n рёбер. Отсюда
следует оценка L(n) 6 n · 2
n
.
С точки зрения физики, КС — матема тические модели схем
из электромагнитных реле.
3.4. Метод каска д ов для пос троения КС и СФЭ
Пусть дана функция f(x
1
, . . . , x
n
). Разложим её по переменной x
1
и введём обозначения:
f(x
1
, . . . , x
n
) = x
1
f(0, x
2
, . . . , x
n
) ∨ x
1
f(1, x
2
, . . . , x
n
).
G
0
:= {f} , g
10
(x
2
, . . . , x
n
) := f (0, x
2
, . . . , x
n
), g
11
(x
2
, . . . , x
n
) := f (1, x
2
, . . . , x
n
), G
1
:= {g
10
, g
11
} .
x
n
x
n
1
0
Изолированная
вершина
Вход
Далее поступа ем с функциями из G
1
так же, как и с f, получаем множество
функций G
2
, и так далее, т. е. на i-том шаге функции из G
i−1
раскладываем по
переменной x
i
и полу ченные функции от n − i переменных помещаем в G
i
, по ка
не достигнем G
n−1
⊆ P
2
(1). Функции множества G
n−1
реализуются просто (см.
рисунок). Теперь мы сможем построить любую функцию из G
i
, если мы уже построили все функции из G
i+1
:
добавим к нужным функциям из G
i+1
рёбра x
i+1
и x
i+1
, руководствуясь разложением данной функции g из G
i
.
Так будем продолжать, пока не дойдём до G
0
= {f }.
∨
&&
¬
x
i+1
g
ij
(0, x
i+2
, . . . , x
n
)
g
ij
(1, x
i+2
, . . . , x
n
)
g
ij
(x
i+1
, . . . , x
n
)
Метод каскадов можно применить и для построения СФЭ. Пусть на очеред-
ном шаге для некоторой функции g
ij
из множества G
i
имеется разложе ние g
ij
=
=
x
i+1
g
ij
(0, x
i+2
, . . . , x
n
) ∨ x
i+1
g
ij
(1, x
i+2
, . . . , x
n
). Тогда навешиваем ФЭ на уже
построенные функции g
ij
(0, x
i+2
, . . . , x
n
) ∈ G
i+1
и g
ij
(1, x
i+2
, . . . , x
n
) ∈ G
i+1
, как
показано на рисунке.
Пример 4.1. Рассмотрим построение КС методом каскадов для ф ункции
f = x
1
⊕ · · · ⊕ x
n
. Разлагая f по x
1
, получим f = x
1
(0 ⊕ x
2
⊕ · · · ⊕ x
n
) ∨ x
1
(1 ⊕
⊕ x
2
⊕ · · · ⊕ x
n
), тогда G
1
= {x
2
⊕ · · · ⊕ x
n
, 1 ⊕ x
2
⊕ · · · ⊕ x
n
}. Разлагая функции
16
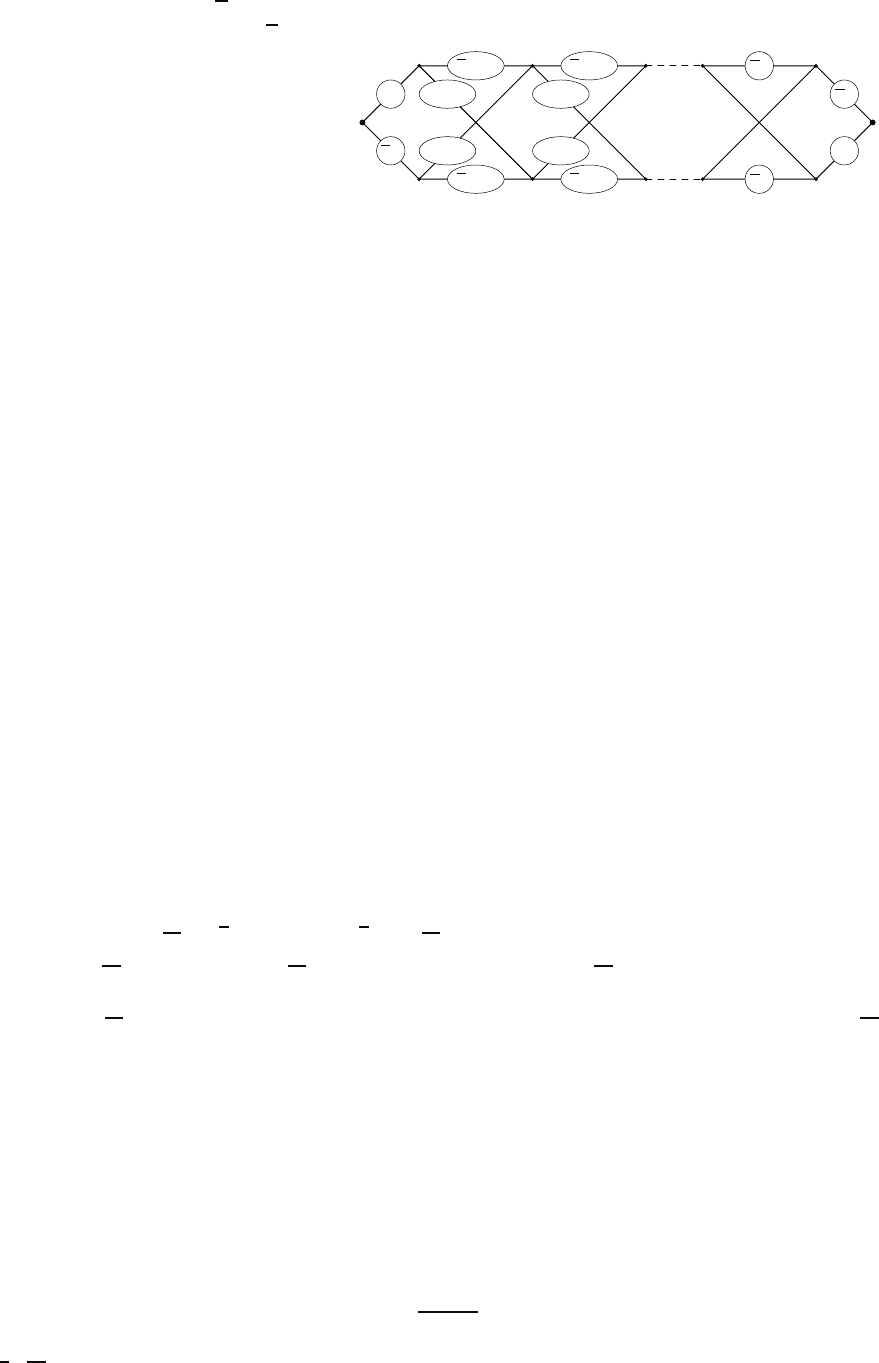
из G
1
по x
2
, получаем x
2
⊕ · · · ⊕ x
n
= x
2
(0 ⊕ x
3
⊕ · · · ⊕ x
n
) ∨ x
2
(1 ⊕ x
3
⊕ · · · ⊕ x
n
)
и 1 ⊕ x
2
⊕ · · · ⊕ x
n
= x
2
(0 ⊕ x
3
⊕ · · · ⊕ x
n
) ∨ x
2
(1 ⊕ x
3
⊕ · · · ⊕ x
n
). Тогда G
2
= {x
3
⊕ · · · ⊕ x
n
, 1 ⊕ x
3
⊕ · · · ⊕ x
n
}.
a
b
x
n
x
n−1
x
n−2
x
2
x
1
x
n−1
x
n−1
x
n−2
x
n−2
x
n
x
n−1
x
n−2
x
2
x
1
Ясно, что |G
i
| = 2, поскольку каждое мно-
жество будет содержать одну однородную и од-
ну неоднородную линейную функцию. Cлож-
ность схемы (см. рисуно к справа) равна 4n− 4,
и можно доказать, что она минимальна.
3.5. Оценка сложнос ти схем при построении методом каскадов
Положим A
s
:= |G
s
|. И з построения множеств G
i
следует, что A
0
= 1 A
i
6 2
i
. С другой стороны, A
i
6 2
2
n−i
,
поскольку G
i
⊆ P
2
(n − i). Обе оценки хороши: перва я полезна, когда i близко к 0, вторая — когда i близко к n.
Значит, при построении число функций сначала растёт, а затем будет быстро уменьшаться — в этом и со с тоит
экономность метода каскадов. На каждом этапе построения мы добавляем не более 2 рёбер. Следовательно , для
контактных схем L(S) 6 2 + 2
n−2
P
i=0
A
i
.
Для СФЭ на i-том шаге можно обойтись 1 + 3A
i
функциональными элементами — одним для отрицания
переменной и тремя (2 конъюнкции и 1 дизъюнкция) для каждой новой функции. Значит, справедлива оценка
L(S) 6
n−2
X
i=0
(1 + 3A
i
) + 3 = n + 2 + 3
n−2
X
i=0
A
i
. (1)
Замечание. Метод каскадов не в с егда даёт схему минимальной с ложности. Для функции f = x
1
⊕ · · · ⊕ x
n
он даёт СФЭ сложности 7n − C, в то время как для неё имеется схема сложности 4n − 4.
Приступим к о ценке суммы
n−2
P
i=0
A
i
. Учитывая оценки для чисел A
i
, разобьём нашу сумму на две части,
учитывая степень влияния каждой из оцено к. Пусть k — «точка разбиения». Представим нашу сумму в виде
n−2
X
i=0
A
i
=
n−k
X
i=0
A
i
+
n−2
X
i=n−k+1
A
i
6
n−k
X
i=0
2
i
+
n−2
X
i=n−k+1
2
2
n−i
< 2
n−k+1
+ (2
2
k−1
+ 2
2
k−2
+ . . . ) . 2
n−k+1
+ 2
2
k−1
.
Здесь первое слагаемое — с умма геометрической прогрессии
2
i
n−k
i=0
, а знак . означает «асимптотически мень-
ше», т. е. отброшенная часть 2
2
k−2
+ 2
2
k−3
+ . . . бесконечно мала по сравнению с оставленной при k → ∞.
Положим ϕ(k) := 2
n−k+1
+ 2
2
k−1
. Строго говоря, для нахождения минимума этой функции следовало бы найти
нуль её производной, а затем в качестве k выбрать ближайшее к этому корню целое число. Уравнение ϕ
′
(k) = 0
легко преобразуется к виду 2
k−1
+ 2k = n + 2 − log
2
ln 2. Однако в явном виде решение указать нельзя, по-
этому мы для оценки воспользуемся то чкой деления k =
log
2
n
. Тогда имеем k > log
2
n − 1, следовательно
ϕ(k) 6 2
n+2−log
2
n
+ 2
2
log
2
n−1
6 4
2
n
n
+ 2
n
2
. Поскольку 2
n
2
= o
2
n
n
при n → ∞, его можно отбросить. Значит, для
КС справедлива оценка 8
2
n
n
, а для СФЭ — 12
2
n
n
. Можно показать, что L(S) ∼
2
n
n
и для СФЭ, и для КС. Здесь
мы не будем этого доказыва ть, но убедимся в её неулучшаемости.
Теорема 3.5. Оце нку
2
n
n
нельзя улучш ить: при всяком n найдётся функция со сложностью, близкой к
2
n
n
.
Введём обозначения: N(n, h) — число функций n переменных сложности не более h, E(n, h) — число
функций сложности ровно h, и S(n, h) — число вс е х схем сложности h.
Докажем, что S(n, h) 6 3
h
(h + n)
2h+1
для СФЭ. В са мом деле, у нас имеется не более 2h входов и h + n
выходов, каждый вход может бы ть присоединён к любому выходу ((h+n)
2h
варианто в), каждый из h элементов
может быть либо отрицанием, либо конъюнкцией, либо дизъюнкцией (3
h
возможностей), кроме того, один выход
помечен ∗ — ещё h + n возможностей. Поэтому оценка для S(n, h) справе длива.
Ясно, что N (n, h) = E(n, h) 6 S(n, h). Действительно, равенство следует из тог о, что люб ую схему сложности
меньше h можно дополнить ничего не делающими э лементами до схемы сложности h, неравенство же следует
из тог о, что различных схем заведомо больше, чем различных функций: одна функция может быть реализов ана
двумя разными схемами, но не наоборот.
Понятно, что если N(n, h
0
) < 2
2
n
= p
2
(n) для некоторого h
0
, то найдётся функция со сложностью больше,
чем h
0
. Логарифмируя данно е неравенство, получаем: log
2
N(n,h
0
)
p
2
(n)
= log
2
N(n, h
0
) − 2
n
< 0. Нужно убедиться
в существовании некоторого h
0
, для которого это неравенство будет справедливо при достат очно больших n.
Возьмём h
0
=
1
3
·
2
n
n
. Имеем
log
2
N(n, h
0
) − 2
n
6 log
2
S(n, h
0
) − 2
n
6 h
0
log
2
3 + (2h
0
+ 1) log
2
(h
0
+ n) − 2
n
. (2)
17

При достаточно больших n имеем log
2
(h
0
+ n) < n, поэтому
log
2
N(n, h
0
) − 2
n
<
log
2
3
3
·
2
n
n
+ (
2
3
·
2
n
n
+ 1)n − 2
n
=
log
2
3
3
·
2
n
n
+ n −
1
3
· 2
n
. (3)
Видно, что при n → ∞ последнее выражение стремится к − ∞, и тем самым неравенство доказано. Таким
образом, мы показали, что L(n) &
1
3
·
2
n
n
. Следовательно, оценку улучшить не удастся.
Для КС можно показать, что S(n, h
0
) 6 (2n)
h
(2h)
2h
. Действительно, для каждого контакта есть 2n возмож-
ностей — x
i
и x
i
, способов их соединения — не более (2h)
2h
, потому что каждый из 2h концов рёбер можно
соединить с каждым. Далее поступаем так же, как и в предыдущем утверждении про СФЭ.
4. Автоматы
4.1. Детерминированные функции
Определение. Алфавит — произвольное конечное множество. Его элементы называются буквами.
Рассмотрим дв а алфавита A = {a
1
, a
2
, . . . , a
n
}, B = {b
1
, b
2
, . . . , b
m
} и функции вида f : A
∞
→ B
∞
, т. е.
функции, преобразу ющие бесконечные последовательности букв A в бесконечные последовательности букв B.
Пример 1.1. Пусть f переводит последовательность, состоящую сплошь из нулей, в себя, а все остальные —
в последова тельность, состоящую сплошь из единиц. Для такой функции существует последователь ность —
состоящая лишь из нулей, для которой невозможно определить её образ, зная лишь конечное число членов. Это
причиняет неудобст ва при вычислении, поэтому введём понятие детерминированности.
Определение. Функция f : A
∞
→ B
∞
называет ся детерминированной, если b(t) однозначно определяется
первыми t членами входной последовательности a(1), a(2), . . . , a(t).
Пример 1.2. Детерминированными функциями являются:
• Функция
0, . . . , 0, 1
t
, ?, . . . , ?, . . .
7→
0, . . . , 0, 1
t
, 1, . . . , 1, . . .
. Здес ь «?» — любой символ.
• Функция чётности b(t) = a(1) ⊕ . . . ⊕ a(t);
• Функция единичной задержки
a(1), a(2), . . . , a(t), . . .
7→
0, a(1), a(2 ), . . . , a(t − 1), . . .
;
• Функция b(t) =
(
1, t = 2
m
;
0, t 6= 2
m
.
Детерминированные функции можно задава ть на бесконечных деревьях. Рассмотрим бинарное дерево, т. е.
такое, что из каждой вершины выходит 2 ребра, и во все вершины, кроме одной (начальной), входит одно
ребро. В начальную вершину рёбра не входят. Каждой бес конечной двоичной по с ледователь ности поставим в
соотв е тствие определённый пут ь на дереве: движение начинается из начальной вершины, и если a(i) = 0, то
идём по левой ветке, а е сли a(i) = 1, то по правой. При этом о чередному зве ну пути приписываем значение
b(i). Легко видеть, что такое соответствие осуществляет биекцию между деревьями и детерминированными
функциями.
0 1
0 1 1 0
0 1 1 0 1 0 0 1
0 1
0 1 1 1
0 1 1 1 1 1 1 1
Пример 1.3. Эти два дерева иллюстрируют
первые два примера детерминированных функ-
ций, приведённых выше.
4.2. Автоматы
Определение. Ограниченно детерминированные функции (конечные автоматы) — детерминированные
функции, деревья которых содержат лишь конечное число различных поддеревьев.
Пронумеруем различные поддеревья. Номера будем писать в начальных вершинах поддеревьев.
1
1 0
0 1
0
0 1
0 1
Пример 2.1. Рассмотрим снова функцию чётности. Её дерево содер-
жит только 2 вида поддеревьев. Эту диаграмму надо понимать так: если
мы находимся в дереве №1 и на входе 0, то выход — 0 и мы остаёмся в
дереве №1, а если на входе 1, то выход — 1 и мы переходим в дерево №0.
Аналогично для дерева №0.
18
В общем случае, если речь идёт о конечно детерминированных функциях, можно утверждать, что достаточно
знание конечного числа конечных фрагмент ов дерева, чтобы найти образ любой последовательности.
Определение. Номера поддеревьев называют ся состояниями автомата.
Фрагменты дерева могут задаваться диаграммами переходов (диаграммами Мура). Они представляют собой
ориентированные графы, вершины которых соответствуют состояниям, а каждому ребру приписыва ется пара
символов, первая компонента которой соответствует входу, а вторая — выходу. Направление ребра соответствует
переходу из одного состояния в другое.
0 1
(1, 1)
(1, 0)
(0, 0) (0, 1)
Пример 2.2. Диаграмма Мура для функции чётности (см. рисунок).
Автомат можно з адават ь функцией перехода q(t + 1) = G
a(t), q(t)
и
функцией выхода b(t) = F
a(t), q(t)
. Здесь q(t) — состояние в момент t.
Удобно считать q(1) = 0. Эти три уравнения называются уравнениями автомата.
0 1
(1, 0)
(0, 1)
(0, 0) (1, 1)
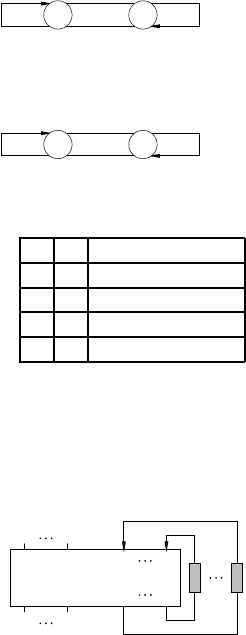
Пример 2.3. Найдём уравнения автомата единичной задержки, т. е.
функции с выходом b(1) = 0, b(t) = a(t − 1), t > 1. Построим диаграмму
Мура (см. рисунок). По ней видно, что q(t + 1) = a(t), а b(t) = q(t). При
этом q(1) = 0.
a q F (a, q), G(a, q)
0 0 (0, 0)
0 1 (1, 0)
1 0 (0, 1)
1 1 (1, 1)
Можно также задавать диаграммы функций таблицами. Н апример, функция
единичной задержки задаётся следующей таблицей:
Теорема 4.1. Любой автомат можно реализовать СФЭ, используя элементы
4 видов: конъюнкцию, дизъюнкцию, отрицание и функцию единичной задержки.
Пусть даны два алфавита A и B. Положим n :=
log
2
|A|
, m :=
log
2
|B|
.
Занумеруем буквы A и B двоичными последовательностями длины n и m соот-
ветственно. Состояния автомата q
0
, . . . , q
λ−1
также занумеруем двоичными последовате льностями длины l :=
:=
log
2
λ
, причём q
0
соотв е тствует (0, . . . , 0). Введём новые функции перехода и выхода, определённые уже на
наборах из 0 и 1:
(
β
1
(t), . . . , β
m
(t)
=
e
F
α
1
(t), . . . , α
n
(t), ω
1
(t), . . . , ω
l
(t)
ω
1
(t + 1), . . . , ω
l
(t + 1)
=
e
G
α
1
(t), . . . , α
n
(t), ω
1
(t), . . . , ω
l
(t)
α
1
α
n
ω
1
ω
l
g
1
g
l
f
1
f
m
Каждая из компонент векторов
e
β и eω реализуется некоторой булевой функцией
(вообще говоря, не всюду определённой). П остроим СФЭ, совместно реализующую
все эти функции (обо з начим их через f
1
, . . . , f
m
и g
1
, . . . , g
l
).
Соединим выходы g
1
, . . . , g
l
через элементы единичной задержки (они показаны
на рисунке прямоугольниками) с входами ω
1
. . . ω
l
. Очевидно, что такая схема будет
работать согласно приведённым выше урав нениям автомата (при условии, что элементы единичной задержки
в первый момент времени выдают нули).
Обратное также верно: любая СФЭ типа той, что была рассмотрена выше, моделирует некоторый автомат.
Замечание. Если разрешить использовать в схеме вместо {¬ & ∨} любые автоматные функции, но запретить
ориентированные циклы, то не сущ ествует такого конечного набора авт оматных функций, схе мой из которых
можно было бы реализовать любой автомат. Иными с ловами, не существует конечной полной системы автоматов.
5. Логика. Исчисления и предикаты
5.1. Исчисление высказываний (ИВ)
Определение. Высказывание — повествовательное сообщение, которое в силу своего смысла может быть
либо истинным, либо ложным.
Пример 1.1. «23.04.2001 — понедельник» — истинное высказывание, «23.04.2001 — вторник» — ложное
высказывание. «Среда ли 23.04.200 1?» — не высказывание.
Истинность высказыва ния будем обозначать 1, ложность — 0 . Встречаются обозначения И, Л (начальные бу к-
вы соответствующих слов), иногда ⊤ и ⊥. Будем рассматривать 4 булевы функции {¬ & ∨ →} и будем строить
над ними тождественно истинные формулы, т. е. принимающие значение 1 при любых значениях аргументов.
Рассмотрим систему аксиом ИВ:
1. Аксиомы, содержащие только импликацию:
а. A → (B → A)
19

б.
A → (B → C)
→
(A → B) → (A → C)
2. Аксиомы, содержащие конъюнкцию:
а. (A&B) → A
б. (A&B) → B
в.
A → B
→
A → C
→
A → (B&C)
3. Аксиомы, содержащие дизъюнкцию:
а. A → (A ∨ B)
б. B → (A ∨ B)
в.
A → C
→
B → C
→
(A ∨ B) → C
4. Аксиомы, содержащие отрицание:
а. (A → B) → (B → A)
б. A → A
в. A → A
Сформулируем правило вывода, вытекающее из свойств импликации: A ≡ 1, (A → B) ≡ 1. Тогда B ≡ 1. Оно
иногда записыва е тся в виде
A→B,A
B
.
Определение. Вывод — конечная последовательность формул {F
1
, . . . , F
s
}, причём любая её формула есть
либо аксиома, либо получается по правилу вывода из предыдущих формул этой последовательности. Формула
называет ся выводимой, если существует вывод, содержащий эту формулу.
Теорема 5.1. Любая выводимая форм ула т ождественно равна 1.
Истинность аксиом легко проверяется путём полного перебора всех возможных на боров значений пере-
менных, в них входящих, что предлагается сделать читателю в качест ве полезног о упражнения. Теперь утвер-
ждение теоремы вытекает из правила вывода.
Пример 1.2. Выведем ф ормулу A → A. По 1.б имеем
A →
(A → A) → A
→
A → (A → A)
→ (A → A)
.
Эта формула имеет вид P → Q, где P = A →
(A → A) → A
. Но P истинна, т.к. она получается из 1.a
подстановкой B = A → A. Значит, можно вывести Q =
A → (A → A)
→ (A → A). Аналогично, она имеет вид
R → X, где R = A → (A → A), а X = A → A. Подставим в 1.a B = A, получим, что R истинна. Итак, истинны
R и R → X. Следовательно, X = A → A выводимо.
Теорема 5.2. Любая тождественно истинная формула выводима, т. е. наш набор аксиом полон.
Мы не будем до казыват ь э ту теорему, поскольку доказательст во очень длинное, но не очень содер-
жательное. Идея доказат е льства состоит в том, что тождественно истинная формула приводится к СДНФ и
переписывается в терминах этой системы аксиом, откуда следует её выводимость.
Определение. Исчисление — конечный набор аксиом A
1
, . . . , A
r
и правил вывода R
1
, . . . , R
q
, каждое из
которых устроено как R
i
=
S
1
i
,...,S
t
i
i
S
i
. Исчисление непротиворечиво, если не существует выводимой формулы,
для которой выводимо и её отрицание.
Пример 1.3. ИВ непротиворечиво, т. к. в нём формула выводима тогда и только т огда, когда она тожде-
ственно истинна. А отрицание тождественно истинной формулы тождественно ложно, значит, невыводимо.
Определение. Система аксиом наз ы вается независимой, если в ней нет аксиомы, выводимой из остальных.
5.2. Предикаты
Определение. n-местный предикат — функция вида P : M
n
→ Ω, где M — некоторое множе с тво, Ω —
множество высказываний. Одноместные предикаты иногда называются свойствами. При n > 1 предикаты
иногда называ ются отношениями.
Пример 2.1. P (x) = «x — чёт ное число» — предикат, определённый, скажем, на множестве N.
Из предикатов можно составлять формулы, используя наши 4 булевы функции. При этом также получаются
предикаты.
Пример 2.2. P (x, y, z, w) = Q(x)&R(y) ∨ S(z, w).
20
