Лупанов О.Б. Лекции по математической логике

Подождите немного. Документ загружается.

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

имени М. В. ЛОМОНОСОВА

Механико-математический факультет

Курс лекций по

математической логике

Лектор — Олег Борисович Лупанов

I курс, 2 семестр, поток математиков

Москва, 2004 г.

Оглавление

1. Булева алгебра 4

1.1. Функции булевой алгебры . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4

1.2. Существенные и несущественные переменные . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4

1.3. Формулы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5

1.4. СДНФ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5

1.5. Полнота систем функций . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6

1.6. Полиномы Жегалкина . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6

1.7. Замкнутые кла ссы функций . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7

1.8. Критерий Поста полноты систем функций . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8

2. k-значная логика 9

2.1. Функции k-значной логики . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9

2.2. Полнота систем функций в P

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10

2.3. Критерии полноты в P

. Теорема Слупецкого – Яблонского . . . . . . . . . . . . . . . . . . . . . . . 11

2.4. Замкнутый класс без базиса . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14

2.5. Класс, имеющий счётный базис . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14

3. Схемы из функциональных элементов 14

3.1. Графы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14

3.2. Схемы из функциональных элементов . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15

3.3. Контактные схемы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16

3.4. Метод каскадов для построения КС и СФЭ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16

3.5. Оценка сложности схем при пос троении методом каскадов . . . . . . . . . . . . . . . . . . . . . . . 17

4. Автоматы 18

4.1. Детерминированные функции . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18

4.2. Автоматы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18

5. Логика. Исчисления и предикаты 19

5.1. Исчисление высказываний (ИВ) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19

5.2. Предикаты . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20

5.3. Кванторы и формулы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21

5.4. Эквивалентные формулы и нормальный вид формулы . . . . . . . . . . . . . . . . . . . . . . . . . 22

6. Алгоритмы 22

6.1. Машина Тьюринга . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22

6.2. Алгоритмически нера зрешимые проблемы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23

Предисловие

Данный документ представляет собой курс лекций «Введение в математическую логику», читаемый деканом

механико-математического факультета МГУ академиком РАН О. Б. Лупановым на I курсе мехмата во втором

семестре. Он наиболее соответствует лекциям, прочитанным в 2001 и 2003 годах, поскольку составлялся на их

основе. В указанные годы в программу из-за недос татка времени не вошла теорема Кузнецова, поэтому здесь

её тоже нет, а всё остальное изложено в полном объёме.

Надо сказать, что этот документ не являе тся свое г о рода первоисточником. Основой для него послужил

тот же курс лекций по логике, набранный в MS Word студентом мехмата с псевдонимом VILenin. Но так как

математические тексты в Word’е выглядят не самым лучшим образом, мы решили улучшить VILenin’ский

вариант. Лекции, свё рстанные заново в L

X’е, выглядят гораздо красиве е и имеют сущес твенно меньший

объём. Кроме того, мы исправили вс е замеченные опеча тки, уточнили некоторые определения и доказательства

некоторых теорем. Насколько хорошо это получилось — пусть судит читатель, и любые обоснованные замечания

будут приняты нами с благодарностью, равно как и любые сообщения о замеченных в нашем издании опечатках.

То, что Вы читаете сейчас, условно можно назв ать третьим изданием. В нём заново сделаны иллюстрации,

исправлены замеченные типографские погрешности, а также ещё нес колько опечаток.

В тексте мы старались не использовать нестандартных обозначений, символов и т. д. Начало и конец дока-

зательства отмечают ся значками  и  соответственно.

Свои вопросы, комментарии, замечания и предложения направляйте на dmvn@mccme.ru, а обновления элек-

тронной версии документа находится на http://dmvn.mexmat.net.

Остаётся поже лать читателю успехов при изучении математической логики, а также удачи на экзамене,

ежели таковой придётся сдавать.

Набор и вёрстка: DMVN Corporation

Последняя редакция: 27 января 2006 г.

1. Булева алгебра

1.1. Функции булевой алгебры

Пусть B = {0, 1}. Рассмотрим функции в ида f : B

→ B. Они называются булевыми функциями или

функциями алгебры логики. Множеств о все х таких функций обоз начается P

. Любую такую функцию можно

задать таблицей:

. . . x

n−1

f(x

, . . . , x

)

0 0 . . . 0 0 f(0, 0, . . . , 0, 0)

0 0 . . . 0 1 f(0, 0, . . . , 0, 1)

. . . . . . . . . . . . . . . . . .

1 1 . . . 1 1 f(1, 1, . . . , 1, 1)

Слева рас положены всевозможные наб оры значений переменных (всего их 2

), а справа значение функции

на этом наборе (0 или 1). Всего функций от n переменных будет p

(n) = 2

. Для экономии места иногда удобно

функцию n переменных задавать строкой из 2

чисел — значений функции, записанных в том порядке, в каком

они были бы расположены в последнем столбце таблицы. Рассмотрим подробнее эти функции.

• n = 1. Здесь всего будет 4 функции:

x 0 x x 1

0 0 0 1 1

1 0 1 0 1

Здесь 0, 1 — константы, x — тождественная функция, x — отрицание x.

• n = 2. Здесь будет 16 функций. Выпишем некоторые:

∨ x

⊕ x

→ x

↓ x

0 0 0 0 0 1 1 1

0 1 0 1 1 1 1 0

1 0 0 1 1 0 1 0

1 1 1 1 0 1 0 0

Здесь x

— конъюнкция или логическое И, x

∨ x

— дизъюнкция или логическое ИЛИ, x

⊕ x

— сумма

по модулю 2, x

→ x

— импликация, x

— штрих Шеффера, x

↓ x

— стрелка Пирса.

1.2. Существенные и несущественные переменные

Определение. Функция f(x

, . . . , x

) называе тся существенно зависящей от переменной x

, если суще-

ствуют два набора значений переменных eα

= (α

, . . . , α

i−1

, 0, α

i+1

, . . . , α

) и eα

= (α

, . . . , α

i−1

, 1, α

i+1

, . . . , α

отличающиеся только значением переменной x

, такие, что f(eα

) 6= f(eα

). В этом случа е говорят, что x

— су-

щественная переменная. Переменная x

называет ся несущественной, если она не является существе нной, т. е.

для любых двух наборов такого вида имеем f (eα

) = f(eα

Пример 2.1. Конъюнкция суще ственно зависит от переменной x

, так как (0&1) 6= (1&1).

Если функция f(x

, . . . , x

) несущественно зависит от x

, то

f(α

, . . . , α

i−1

, 0, α

i+1

, . . . , α

) = β, f(α

, . . . , α

i−1

, 1, α

i+1

, . . . , α

) = β.

Её таблица имеет следующий вид:

. . . x

i−1

i+1

. . . x

f(x

, . . . , x

)

. . . . . .

. . . α

i−1

0 α

i+1

. . . α

. . . . . .

. . . α

i−1

1 α

i+1

. . . α

. . . . . .

Вычеркнем все наборы, у которых x

= 1, и i-й столбец, получим новую функцию g(x

, . . . , x

i−1

, x

i+1

, . . . , x

такую что g(α

, . . . , α

i−1

, α

i+1

, . . . , α

) = f(α

, . . . , α

i−1

, 0, α

i+1

, . . . , α

). Её таблица имеет вид

. . . x

i−1

i+1

. . . x

g(x

, . . . , x

i−1

, x

i+1

, . . . , x

)

. . . . . . . . .

. . . α

i−1

i+1

. . . α

f(α

, . . . , α

i−1

, 0, α

i+1

, . . . , α

)

. . . . . . . . .

Говорят, что функция g получилас ь из функции f отбрасыванием несущественной переменной x

Аналогично можно и добавлять несущественные переменные. Пусть дана функция f(x

, . . . , x

), построим

новую функцию h(x

, . . . , x

, x

n+1

) = f(x

, . . . , x

). Тогда x

n+1

будет несущественной переменной ф ункции h,

действительно, h(α

, . . . , α

, 0) = f(α

, . . . , α

) = h(α

, . . . , α

, 1). Говорят, что функция h получилась из функ-

ции f добавлением несущественной переменно й x

n+1

Определение. Функции h

и h

называются равным и, если одна получена из другой в результате добавления

и отбрасывания несущественных переменных.

Пример 2.2. Пусть да на функция h

, x

), несущественно зависящая от переменной x

, отбросим её,

получим ф ункцию g(x

), добавим несущественную переменную x

, по лу чим функцию h

, x

). Функции h

равны, хотя таблицы у них разные!

, x

)

0 0 0

0 1 1

1 0 0

1 1 1

→

g(x

)

0 0

1 1

→

, x

)

0 0 0

0 1 0

1 0 1

1 1 1

1.3. Формулы

Определение. Пусть дано некоторое множество функций F = {f

, . . . , x

), . . . , f

, . . . , x

), . . . }.

Определим понят ие формулы над множеством F индуктивно. Функции f

, . . . , x

) являются формулами

над F. Если A

, . . . , A

— переменные или формулы над F, то f

, . . . , A

) тоже является формулой над F.

Пример 3.1. F = {ϕ(x

, x

)}, тогда ϕ(x

, x

) и ϕ



, ϕ(x

, x

)



будут формулами над F, а ϕ(x

, x

) —

нет.

Значение переменной x

на наборе R = (α

, . . . , α

) равно α

. Пусть уже определены A

, . . . , A

. Тогда

, . . . , A

)

= f



, . . . , A



. (1)

Отсюда следует, что любая формула в ы ражает некоторую функцию.

Определение. Формулы называются эквивалентными (рав ными), если они выражают равные функции.

Рассмотрим множество функций F = {x

, x

∨ x

, x

}. Примеры равных формул над F:

= x

, x

∨ x

= x

, x

= x

∨ x

, (x

∨ x

)&x

= (x

) ∨ (x

Введём ещё одну полезную функцию:

(

x, σ = 1;

x, σ = 0.

(2)

Заметим, что x

= 1 ⇔ x = σ. В самом деле, x

= 1 ⇔ x = 1 , и x

= x = 1 ⇔ x = 0.

Введём с оглашения по записи формул. Знак & можно не писать, как умножение в алгебре. Для ассоциа-

тивных операций внутренние скобки писать не будем:





∨ x

) ∨ x



∨



∨ x





= (x

∨ x

Внешние скобки также можно опускать и писать x

⊕x

вместо (x

⊕x

). Иногда будем использовать для записи

отрицания знак ¬x = x, а для конъюнкции — знак «∧». Введём сокращения:

& . . . &A

i=1

, A

∨ · · · ∨ A

i=1

, A

⊕ · · · ⊕ A

i=1

1.4. СДНФ

Рассмотрим формулу x

. . . x

. Она равна единице только на одном наборе (σ

, . . . , σ

Теорема 1.1 (О разложении функции по пере менным). Дана функция f(x

, . . . , x

) и число 1 6 k 6 n.

Имеет место формула для f над множеством {∨, &, ¬, f (x

, . . . , x

), 0, 1}:

f =

(σ

,...,σ

)

· . . . · x

f(σ

, . . . , σ

, x

k+1

, . . . , x

). (3)

 Возьмём произволь ный набор eα = (α

, . . . , α

) и найдём значение формулы на этом наб оре. В том

случае, когда (α

, . . . , α

) = (σ

, . . . , σ

), имеем α

·. . . ·α

f(σ

, . . . , σ

, α

k+1

, . . . , α

) = f (eα). Если (σ

, . . . , σ

) 6=

6= (α

, . . . , α

), то α

· . . . · α

f(σ

, . . . , σ

, α

k+1

, . . . , α

) = 0. Следо вательно , расписав (3) по всем наборам,

получим 0 ∨ . . . ∨ 0 ∨ f (x

, . . . , x

) ∨ 0 ∨ . . . ∨ 0 = f (x

, . . . , x

). 

Рассмотрим два частных случая для числа k.

◦

k = 1. f (x

, . . . , x

) = x

f(0, x

, . . . , x

) ∨ x

f(1, x

, . . . , x

◦

k = n. Для дизъюнкции надо б рать лишь наборы eσ = (σ

, . . . , σ

), для которых f(eσ) = 1, так как все

остальные дизъюнкты обнулятся:

f(x

, . . . , x

) =

eσ: f (eσ)=1

. . . x

Это формула для f над { ¬ & ∨}. Она называется совершенной дизъюнктивной нормальной формой (СДНФ).

Пример 4.1. x → y = x y ∨ x ∨ xy, x ⊕ y = xy ∨ xy, x ∼ y = x y ∨ xy, где x ∼ y = (1001).

1.5. Полнота систем ф ункций

Определение. Система F называется полной, если любая функция из P

выражается формулой над F.

Теорема 1.2 (До статочное условие полноты). Пусть дана полная си стема F, и любая функция из F

выражается формулой над системой G. Тогда G — полная.

 Пусть F = {f

, f

, . . . } и F

— формулы над G, выражающие функции f

соотв е тственно. Возьмём

произвольную функцию f ∈ P

, тогда суще с твует формула F

над F, выражающая эту функцию. Заменим в

формуле каждую из функций f

на соответствующую ей формулу F

, и получим фо рмулу над G, выражающую

функцию f. Значит, любая функция из P

выражается формулой над G, поэтому система G — полная. 

Теорема 1.3. Из любой полной системы можно выделить конечную полную подсистему.

 Пусть F — полная сист е ма (возможно, бесконечная), тогда существу ют формулы над F, выражающие

функции ¬, &, ∨. В каждую из этих формул входит конечное число функций из F, значит, эти функции образуют

конечную подсистему G. Так как функции ¬, &, ∨ выражаются формулами над G, а {¬ & ∨} — полная система,

то G будет конечной полной подсистемой. 

Используя достаточное условие полноты, построим ещё несколько полных с истем:

1. {& ¬}. Действительно, конъюнкция и отрицание у нас есть. Так как x

∨ x

= x

, то и дизъюнкция

тоже есть. Значит, система полная.

2. {∨ ¬}. Аналогично, так как x

= x

∨ x

3. {⊕ & 1}. Конъюнкция уже есть, отрицание выразим так: x = x ⊕ 1. З начит, сист ема полная.

4. {/} — штрих Шеффера: x = x/x, а x

= x

= (x

)



). Значит, система является полной.

5. {↓} — стрелка Пирса — тоже полная система. Доказательство — аналогично предыдущему.

1.6. Полиномы Жегалкина

Рассмотрим конъюнкции вида x

. . . x

, где все i

, . . . , i

— различны. Также будем рассматрива ть конъ-

юнкции длины 1 (т. е. переменные) и константу 1 (конъюнкцию длины 0 ).

Определение. Сумма по модулю 2 попарно различных коньюнкций

,...,i

)

. . . x

называет ся полиномом Жегалкина. Пустой полином Жегалкина по определению выражает нулев ую функцию.

Степенью полинома называется максимальная длина конъюнкций переменных , входящих в него.

Теорема 1.4 (Жегалкина). Любая функция алгебры логики представима в виде полинома Жегалкина

единственным образом с точностью до перестановки слагаемых и пере становки множителей в слагаемых.

 Представимость. Так как {⊕ & 1} — полная система, то любая функция представима формулой над

{⊕ & 1}. Приве дём эту фо рмулу к полиному Жегалкина:

◦

Раскроем все скобки, применив дистрибутивный закон (A ⊕ B)C = AC ⊕ BC. Тогда формула приведётся

к сумме конъюнкций A

⊕ · · · ⊕ A

◦

Так как xx = x, то, если в каком-либо произведении встречаются повторяющиеся переменные, можно

оставить только один экземпляр.

◦

Уничтожим лишние единицы: x&1 = x, поэтому ес ли в каком-либо произведении встречаются единицы,

можно их убрать (лишь в случае произведения только из единиц оставим одну единицу).

◦

Приведём подобные: x⊕x = 0, значит, е с ли есть по вторяющиеся слагаемые, оба экземпляра можно убра ть.

Если пропадут все слагаемые, это будет пустой полином.

В итоге мы получим полином Жегалкина. Тем самым представимость доказана.

Единственность. Поскольку в любое произведение любая переменная может входить или не входить, то

всего различных произведений из n переменных будет 2

, но из них нужно уб рать нулев ое произведение и

добавить константу 1, т. е. всего ра ссматриваемых нами произведений будет тоже 2

. Так как в полиноме любое

произведение может присутствовать или не присутствовать, всего различных полиномов (включая пустой) будет

ровно 2

, т. е. столько же, сколько всех функций в P

(n). Поэто му, если какая-нибудь функция представима

в виде двух различных полиномов Жегалкина, то какая-то функция не будет представима в этом виде, что

невозможно. 

1.7. Замкнутые классы функций

Определение. Замыканием системы F называется множество [F], состоящее из всех функций, вы ражаемых

формулой над F. Система F называется замкнутой, если F = [F].

Свойства операции замыкания:

◦

F ⊆ [F].

◦

⊆ F

⇒ [F

] ⊆ [F

◦

∪ F

] ⊇ [F

] ∪ [F

◦



[F]



= [F].

◦

Если F — полная система, то [F] = P

Определение. Функции, представимые полиномами Жегалкина первой степени, называются линейными.

Линейные функции имеют вид x

⊕ · · · ⊕ x

⊕c, где c ∈ B. Их множество обозначается через L. Оно, очевидно,

является замкнутым. Это множест во нетривиально, т. е. L 6= ∅, L 6= P

Лемма 1.5 (О нелинейной функции). Из любой нелинейной функции, подставляя вместо некоторых

переменных константы, и, может быть, отрицание переменных, и, может быть, навешивая отрицание на

результат, можно получить конъюнкцию двух пе ременных.

 Пусть f(x

, . . . , x

) /∈ L, тогда в её полиноме Жегалкина есть произведение длины больше 1. Возьмём

самое короткое из них, переставим его на перв ое место: f(x

, . . . , x

) = x

. . . x

⊕ . . . , p > 2.

Каждое другое нелинейное произведение содержит хотя бы одну переменную, отличную от x

, . . . , x

. Вме-

сто этих переменных, кроме x

, . . . , x

, подставим 0, тогда все остальные нелинейные конъюнкции обратятся

в 0, и останется f (x

, . . . , x

, 0, . . . , 0) = x

. . . x

⊕ l(x

, . . . , x

), где l(x

, . . . , x

) — линейная функция от пе-

ременных x

, . . . , x

. Оставим первые две переменные, а вместо остальных (если они есть) подставим 1, по-

лучим f(x

, x

, 1, . . . , 1, 0, . . . , 0) = x

⊕ l(x

, x

) = x

⊕ αx

⊕ βx

⊕ γ. Сделаем следующую подстановку:

вместо x

подставим x

⊕ β (это будет либо x

, либо x

), x

заменим на x

⊕ α и прибавим ко всей функ-

ции (αβ ⊕ γ), т. е. либо ничего не изменим, либо навесим отрицание на результат. В ит оге получится следу-

ющая функция: (x

⊕ β)(x

⊕ α) ⊕ α(x

⊕ β) ⊕ β(x

⊕ α) ⊕ γ ⊕ (αβ ⊕ γ). После раскрытия с кобок получим

⊕ αx

⊕ βx

⊕ αβ ⊕ αx

⊕ αβ ⊕ βx

⊕ αβ ⊕ γ ⊕ αβ ⊕ γ = x

. 

Следствие 1.1. Если f /∈ L, то & ∈



{f, 0, 1, ¬}



Рассмотрим ещё два замкнутых класса:

◦

Класс T

функций, таких, что f(0, . . . , 0) = 0. Очевидно, что это множе ство нетривиально.

Утверждение 1.6. Класс T

замкнут.

 Сами переменные принадлежат этому множеству: если f (x) = x, то f(0) = 0. Поэтому достаточно

доказать, что если f (x

, . . . , x

) ∈ T

и f

, . . . , f

∈ T

, то и f (f

, . . . , f

) ∈ T

. Поскольку f

(0, . . . , 0) = 0, то



(0, . . . , 0), . . . , f

(0, . . . , 0)



= f (0, . . . , 0) = 0. С ледователь но, класс T

замкнут. 

◦

Класс T

функций, таких, что f(1, . . . , 1) = 1. Этот класс тоже нетривиален и з амкнут.

Определение. Функция f

∗

, . . . , x

) := f (x

, . . . , x

) называ е тся двойственной к f(x

, . . . , x

). Функция

f называется самодвойственной, если f

∗

= f .

Пример 7.1. x

∗

= x = x, x

∗

= x = x, (x

)

∗

= x

∨ x

, (x

∨ x

)

∗

= x

, 0

∗

= 0 = 1, 1

∗

= 1 = 0.

Множество самодвойственных функций обоз начается через S. Очевидно, что S нетривиально.

Утверждение 1.7. Класс S замкнут.

 Ясно, что переменные входят в S, поэтому нам опять достаточно доказать, что если f (x

, . . . , x

) ∈ S

и f

, . . . , f

∈ S, то и f (f

, . . . , f

) ∈ S. Можно считать, что у всех функций f

одинаковый набор переменных,

поскольку если это не так, то недостающие переменные можно добавить как несущественные. Пусть этот набор —

, . . . , y

. Пусть g(y

, . . . , y

) = f



, . . . , y

), . . . , f

, . . . , y

)



. Тогда

∗

, . . . , y

) = f



, . . . , y

), . . . , f

, . . . , y

)



= f



, . . . , y

), . . . , f

, . . . , y

)



= f



∗

, . . . , y

), . . . , f

∗

, . . . , y

)



= f

∗



∗

, . . . , y

), . . . , f

∗

, . . . , y

)



= g(y

, . . . , y

поскольку f, f

, . . . , f

∈ S. 

Замечание. Пусть f(x

, . . . , x

) ∈ S, тогда

f(x

, . . . , x

) = f(x

, . . . , x

) ⇔ f(x

, . . . , x

) = f(x

, . . . , x

) ⇔ f(x

, . . . , x

) = f(x

, . . . , x

т. е. на про тивоположных наборах переменных значения функции противоположны.

Лемма 1.8 (О не самодвойственной функции). Пусть f (x

, . . . , x

) /∈ S, тогда, подставляя в неё вме-

сто переменной x

переменную x или x, можно получить константу.

 Поскольку f (x

, . . . , x

) /∈ S, то существует пара противопо ложных наборов (α

, . . . , α

) и (α

, . . . , α

f(α

, . . . , α

) = f(α

, . . . , α

). Заменим x

на x

⊕α

, т. е. вместо x

поставим либо x

, либо x

, и получим функцию

h(x) = f(x ⊕ α

, . . . , x ⊕ α

), а поскольку h(0) = f(α

, . . . , α

), h(1) = f(α

, . . . , α

), получаем, что h(0) = h(1),

т. е. h(x) является константой. 

Следствие 1.2. Если f /∈ S, то {0, 1} ⊂



{f, ¬}



 По лемме одна из констант уже есть. С помощью от рицания можно получить и вторую константу. 

Введём правило сравнения на боров. Будем говорить, чт о (α

, . . . , α

) 6 (β

, . . . , β

), если α

6 β

, i = 1, n.

При э том мы считаем, что 0 6 0, 0 6 1, 1 6 1, но 1  0. Теперь мы можем упорядочить (частично!) все наборы:

(0, . . . , 0) 6 (α

, . . . , α

) 6 (1, . . . , 1).

Определение. Функция f(x

, . . . , x

) называе тся монотонной, если ∀ (α

, . . . , α

) 6 (β

, . . . , β

) имеем

f(α

, . . . , α

) 6 f(β

, . . . , β

). Множество всех монотонных функций о бозначается M.

Пример 7.2. Функции 0, 1, x, x

монотонны (это видно из таблицы), а функции x, x

— нет.

Как мы видим из примеров, множество функций M нетривиально.

Утверждение 1.9. Класс M замкнут.

 Переменные принадлежат этому множеству, значит, достаточно доказат ь, что из f (x

, . . . , x

) ∈ M

и f

, . . . , f

∈ M следует, что f (f

, . . . , f

) ∈ M. Будем считать, что f

, . . . , f

— ф ункции от одного набора

переменных y

, . . . , y

, иначе доб авим их как несущественные. В силу монотонно с ти функций f

для любых

двух наборов eα = (α

, . . . , α

) 6 (β

, . . . , β

) =

β будем иметь, что f

(eα) 6 f

(

β), т. е.



(eα), . . . , f

(eα)





(

β), . . . , f

(

β)



, но так как f монотонна, то f



(eα), . . . , f

(eα)



6 f



(

β), . . . , f

(

β)



⇒ f (f

, . . . , f

) ∈ M. 

Лемма 1.10 (о немонотонной функции). Из любой немонотонной функции, подставл яя вм есто неко-

торых ее переменных константы, можно получить отрицание.

 Пусть f (x

, . . . , x

) /∈ M. Тогда с уществуют два набора eα = (α

, . . . , α

) 6 (β

, . . . , β

) =

β, такие,

что f(eα)  f(

β), т. е. f(eα) = 1 и f (

β) = 0. Поэтому наб оры eα и

β разные. Переставим те переменные,

по которым они отличаются, на первые места, т огда эт и наборы превратятся в (0, 0, . . . , 0

| {z }

, α

m+1

, . . . , α

) и

(1, 1, . . . , 1

| {z }

, β

m+1

, . . . , β

). Будем последовательно заменят ь в наборе с нулями в начале эти нули на единицы,

тогда рано или поздно наступит момент, при котором значение функции сменится на противоположное, по-

скольку на наборе с единицами значение функции противоположное. Значит, зафиксировав все переменные,

кроме той, на которой произо шла смена значения, мы получим отрицание. 

1.8. Критерий Поста полноты сис тем функций

Определение. Базис системы функций F — такая подсистема B ⊆ F, что F ⊆ [B], и ни одной функции

из B выкинуть нельзя.

Теорема 1.11 (Критерий Поста). Система F полна тогда и только тогда, когда она не содержится

целиком ни в одном из классов T

, T

, L, S, M.

 Необходимость. Если F целиком содержится в каком-либо из этих классов, то и [F] содержится в нём

и потому не совпадает с P

, а значит, система F неполна я.

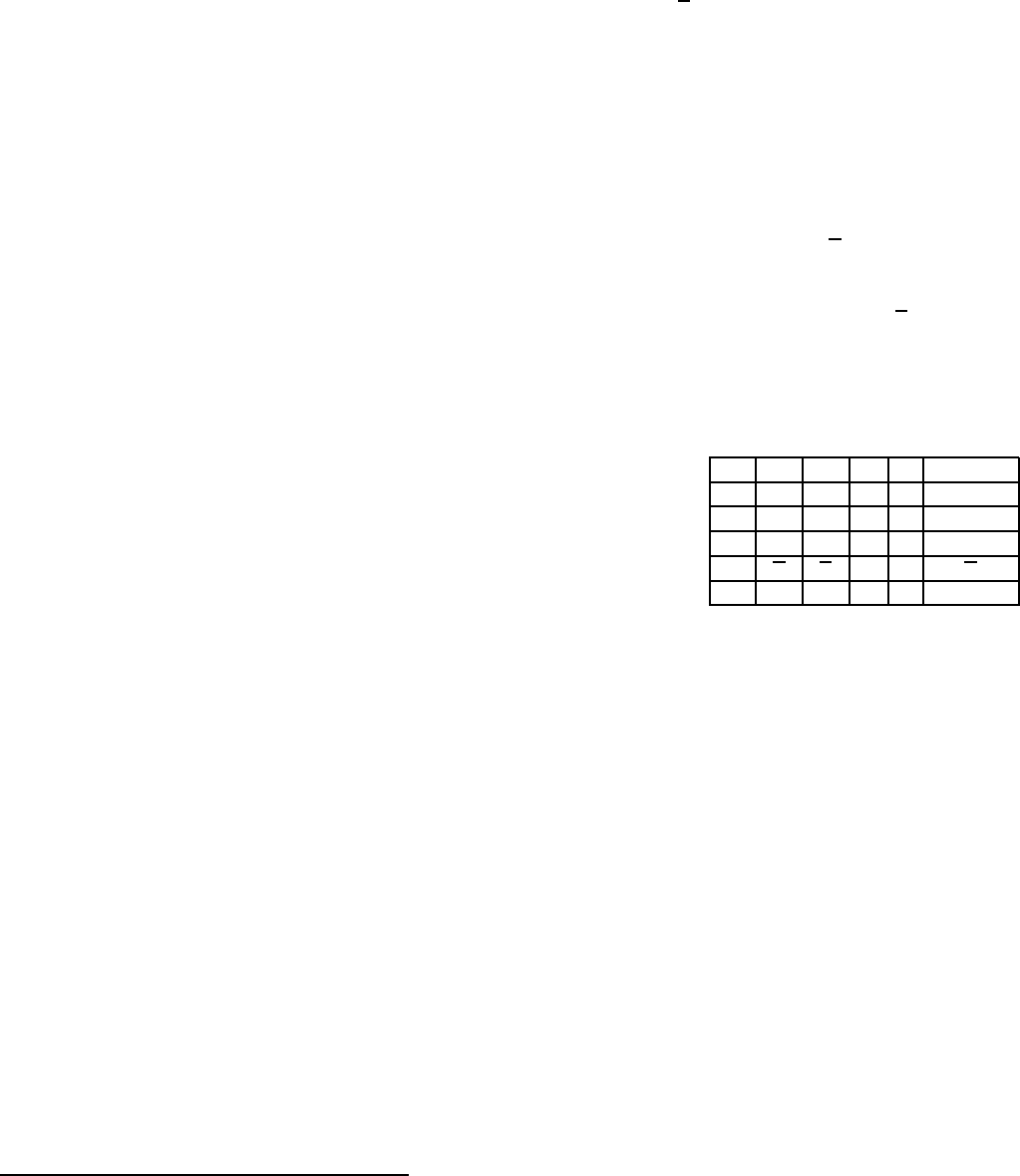
Достаточность. Так как F * T

, то найдется f

∈ F, не лежащая в T

. Аналогично в F найдутся f

/∈ T

/∈ L, f

/∈ S, f

/∈ M. Сейчас мы получим из них константы, отрицание и конъюнкцию. Поскольку f

/∈ T

имеем f (0, . . . , 0) = 1. Положим ϕ(x) := f (x, . . . , x) ⇒ ϕ(0) = 1. Если ϕ(1) = 1, то это константа 1, а функция

ψ(x) := f

(ϕ(x), . . . , ϕ(x)) — константа 0. Если же ϕ(1) = 0, то ϕ(x) = x, и по лемме о несамодвойственной

функции при помощи отрицания можно получить обе константы. По лемме о немоното нной функции из f

, имея

константы, можно получить отрицание. По лемме о нелинейной функции при помощи констант и отрицания

можно получить конъюнкцию. Таким образом, мы в ыделили в F полную подсистему, а значит, [F] = P

. 

Следствие 1.3. Из любой полной системы можно в ыделить полную подсистему, состоящую из 5 функ-

ций.

 Достаточно взять функции f

, f

. 

Теорема 1.12. Можно обойтись и 4 функциями, но меньшего количества в общем случае уже не хватит.

 Докажем, что 4 функций достаточно. В случае, когда ϕ(x) = 1 (здесь ϕ — функция из предыдущей

теоремы), это несамодвойственная функция, и можно обойтись без f

. Если же ϕ(x) = x, это немонотонная

функция, можно обойтись без f

Приведём пример базиса из 4 функций: F = {0, 1, x

, x

⊕ x

}. Имеем 1 /∈ T

, 0 /∈ T

, x

/∈ L, 0 /∈

S, x

⊕ x

/∈ M. Функция x

⊕ x

немонотонная, т.к. из неё можно получить отрицание: x = 1 ⊕ 0 ⊕ x.

Она самодвойственная, т.к. (x

⊕ x

)

∗

= x

⊕ 1 ⊕ x

⊕ 1 ⊕ 1 = x

⊕ x

. Отсюда следует, что

[F] = P

, но ни одну функцию из F выкинуть нельзя, так как все, кроме 0, входят в T

; все, кроме 1, входят в

; все, кроме x

, входят в L; и вс е, кроме x

⊕ x

, входят в M. 

Лемма 1.13. Д ля любых двух классов среди T

, T

, L, S, M существует функция, принадлежащая одному

и не принадлежащая другому.

L S M

0 & 0 x

⊕ x

1 & 1 x

→ x

L 1 0 1 x

⊕ x

S x x ψ x

M 1 0 & 1

 Просто предъявим требуемые функции для всех пят и классов. В

таблице в каждой клетке стоит функция, принадлежащая классу строки

и не принадлежащая классу сто лбца. Функцию ψ определим следующим

образом: ψ(x

, x

) := (0, 0, 0, 1, 0, 1, 1, 1). Проверим её свойства: очев ид-

но, что она самодвойственная (вспомните определение!). Она нелинейная,

так как ψ(0, x

, x

) = x

. 

Теорема 1.14. Пусть A = [A], A 6= P

⇒ A содержится в одном из пяти классов T

, T

, L, S, M.

 Пусть A не содержится ни в одном из этих классов. По критерию Поста A = [A] = P

. Противоречие. 

Определение. F называется предполным классом, если F = [F] 6= P

и ∀ f /∈ F имеем



{F, f}



= P

Теорема 1.15. В P

существует ровно 5 предполных классов T

, T

, L, S, M, и других нет.

 Докажем, что любой из этих классов (например, S) – предполный. Первые два условия, очевидно,

выполнены. По предыдущей лемме в нём есть функции, не принадлежащие T

, T

, L, M соответственно, а тогда

∀ f /∈ S в системе S ∪{f} ес ть функции, не принадлежащие ни одному из этих классов. Значит, S — предполный

класс.

Теперь докажем, что других предполных кла ссов нет. Допустим, A = [A] 6= P

, и A не совпадает ни с одним

из эт их пят и классов. Тогда по предыдущей т еореме A содержится в одном из них (обозначим его через X ).

A 6= X , A ⊆ X ⇒ ∃ f /∈ A, f ∈ X ⇒ A ∪ {f} ⊆ X ⇒

A ∪ {f}

⊆ X 6= P

. Значит, система A ∪ {f} неполная, а

тогда по определению A — не предполный класс. 

Теорема 1.16 (E. Po st). В P

имеется с чётное множество замкнутых классов.

2. k-значная логика

2.1. Функции k-значной логики

Аналогично функциям двузначной логики можно определить функции k-значной логики. Значения перемен-

ных и самих функций лежат в множестве {0, 1, . . . , k − 1}. Множество всех таких функций обозначается через

. Аналогично эти функции можно задавать таблицей:

Доказательства этой теоремы в нашем курсе не будет.

. . . x

f(x

, . . . , x

)

0 . . . 0 f(0, . . . , 0)

. . . . . .

. . . α

f(α

, . . . , α

)

. . . . . .

k − 1 . . . k − 1 f(k − 1, . . . , k − 1)

Количество различных наборов значений равно k

, на каждом наборе функция может принимать k значений,

следовате льно, всего функций будет p

(n) = k

. Понятия формулы, значения формулы, существенной зависи-

мости, полноты и т.д. вводятся также, как в булевой алгебре. Однако ест ь и существенные отличия. Приведём

одно из них. В двузначной логике имеет место следующее

Утверждение 2.1. Пусть f(x

, . . . , x

) и g(y

, . . . , y

) существенно зависят от всех своих пе ременных.

Тогда функция h(x

, . . . , x

n−1

, y

, . . . , y

) := f



, . . . , x

n−1

, g(y

, . . . , y

)



также существенно зависит от всех

своих переменных.

 Все переменные равноправны, поэто му достаточно доказать утверждение для x

и y

. Переменная x

—

существенная для f , поэтому найдутся наборы eα

= (0 , α

, . . . , α

) и eα

= (1 , α

, . . . , α

), такие, что f(eα

) 6=

6= f (eα

). Но так как g 6= cons t, то на йдётся набор

β, такой, что g(

β) = α

. Значит, f



0, α

, . . . , α

n−1

, g(

β)



= f(eα

) 6= f (eα

) = f



1, α

, . . . , α

n−1

, g(

β)



. Значит, h существенно зависит от x

. Поскольку f существе нно

зависит от x

, то найдутся наборы eγ

= (γ

, . . . , γ

n−1

, 0) и eγ

= (γ

, . . . , γ

n−1

, 1), такие, что f(eγ

) 6= f ( eγ

). Ана-

логично найдутся

= (δ

, . . . , δ

m−1

, 0) и

= (δ

, . . . , δ

m−1

, 1), такие, что g(

) 6= g(

). Тогда h обнаруживает

существенную зав исимо с ть от y

на наборах (γ

, . . . , γ

n−1

, δ

, . . . , δ

m−1

, 0) и (γ

, . . . , γ

n−1

, δ

, . . . , δ

m−1

, 1). 

Это утверждение перестаёт быть верным в k-значной логике при k = 3. Рассмотрим функцию ϕ(x, y) =

= (0, 0, 0, 0, 0, 0, 0, 0, 1), которая равна 1 только на наборе (2, 2). То гда ϕ



x, ϕ(y, z)



— константа 0, пото му что

для любых y и z имеем ϕ(y, z) 6= 2.

Интересными для рассмотрения функциями в k-значной логике являются:

• Константы 0, 1, . . . , k − 1;

• Тождественная функция x;

• Аналоги отрицания x + 1 (mod k) и N(x) := k − 1 − x;

• Аналоги функции x

: J

(x) :=

(

k − 1, x = σ;

0, x 6= σ

и j

(x) :=

(

1, x = σ;

0, x 6= σ

• Аналоги конъюнкции min(x

, x

) (далее — &) и x

(mod k);

• Аналоги дизъюнкции max(x

, x

) (далее — ∨) и x

+ x

(mod k).

2.2. Полнота систем ф ункций в P

Утверждение 2.2. Система {0, 1, . . . , k − 1 J

(x), . . . , J

k−1

(x) min(x

, x

) max(x

, x

)} — полная.

 В P

имеет место ана лог СДНФ:

f(x

, . . . , x

) =

(σ

,...,σ

)

)& . . . &J

)&f(σ

, . . . , σ

Действительно, подставим (α

, . . . , α

) в f и проверим равенство. Если (α

, . . . , α

) = (σ

, . . . , σ

), то име-

ем J

(α

)& . . . &J

(α

)&f(σ

, . . . , σ

) = f(σ

, . . . , σ

), поскольку J

(σ

) = k − 1 — максимально возможному

значению. Если же (α

, . . . , α

) 6= (σ

, . . . , σ

) ⇒ ∃ i: σ

6= α

⇒ J

(α

) = 0 — минимально воз можному значе-

нию, следовательно, J

(α

)& . . . &J

(α

)&f(σ

, . . . , σ

) = 0. Значит, формула верна и мы предъявили явное

выражение для произвольной функции над заданным множеством. 

Следствие 2.1. Для любого k существуют конечные полные системы.

Утверждение 2.3. Система {x + 1 (mod k), max(x

, x

)} — полная.

 Здесь и далее арифметические операции подразумевают ся по модулю k (для краткости). Из функции

x + 1 многократным применением можно получить функцию вида x + c, где c — константа. Далее, заметим, что

max



x, x + 1, . . . , x + (k − 1)



= k − 1. Из этой константы можно получить в с е остальные. Теперь рассмотрим

функцию ϕ

(x) := max



x, x + 1, . . . , x + (t − 1), x + (t + 1), . . . , x + (k − 1)



+ 1 и заметим, что

(x) =

(

k − 1, x = k − 1 − t;

0, x 6= k − 1 − t,

то есть ϕ

(x) = J

k−1−t

(x).