Лиман С.А., Радов С.Г. Математическая обработка маркшейдерско-геодезических измерений
Подождите немного. Документ загружается.

61
литном ходе с
N
определяемыми точками измеряется
N
+
2
углов и
N
+ 1
линий, т.е.
n
= 2
N
+
3
, а необходимых неизвестных k = 2 N, т.е. при коррелатном способе уравнива
ния решается
система из 3 нормальных уравнений.
Решение и контроль решения нормальных уравнений осуществляется по алгорит
му
Гаусса так же. Как
при параметрическом способе уравнивания.
9.3 Пример уравнивания нивелирной сети коррелатным способом
h4 = +0,080
h3 = -0,120
h2 = +2,068
HRp3 = 107,520
HRp2 = 103,070
HRp1 = 100,000
3
2
1
h6 = -2,170
h5 = +4,266
h1 = -1,110
RpA RpB
RpC
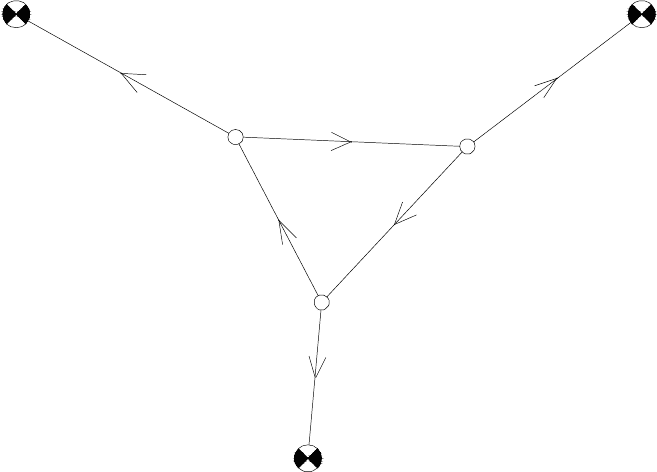
Рисунок 9.1 – Схема нивелирной сети
Условные уравнения связи имеют вид:
ϕ
1
= H
A
- h
1
* + h
2
* + h
3
* - H
B
= 0
ϕ
2
= h
2
* + h
4
* + h
6
* = 0
ϕ
3
= H
B
– h
3
* + h
4
* + h
5
– H
C
= 0
Свободные члены вычисляются по формулам:
w
1
= H
A
- h
1
* + h
2
* + h
3
* - H
B
w
2
= h
2
* + h
4
* + h
6
*
w
3
= H
B
– h
3
* + h
4
* + h
5
– H
C
Или вместо любого из этих уравнений можно подставить:
ϕ = H
A
+ h
1
* - h
6
* + h
5
* - H
C
= 0
Условные уравнения поправок будут иметь вид:
-1 v
1
+ 1 v
2
+ 1 v
3
+ 0 v
4
+ 0 v
5
+ 0 v
6
+ w
1
= 0
0 v
1
+ 1 v
2
+ 0 v
3
+ 1 v
4
+ 0 v
5
+ 1 v
6
+ w
2
= 0

62
0
v
1
+ 0
v
2
-
1
v
3
+ 1
v
4
+ 1
v
5
+ 0
v
6
+
w
3
= 0
Если измерения равноточные, то P = Q = E. Нормальные уравнения (A A
T
) K + W = 0.
3
13
113
010
100
110
101
011
001
011
101
000
100
010
111 −
=
−
−
⋅
−
−
=
T
AA
Для составления нормальных уравнений все вычисления ведутся в таблице.
Таблица 9.1 – Вычисление коэффициентов нормальных уравнений.
№№ хода
C
L
q =
a
1i
a
2i
a
3i
f S v
1
2
3
4
5
6
W
j
w
1
w
2
w
3
[pv
2
]=
Система нормальных уравнений
N
1i
N
11
N
12
N
13
N
1F
N
1S
N
2i
N
21
N
22
N
23
N
2F
N
2S
N
3i
N
31
N
32
N
33
N
3F
N
3S
N
FF
N
FF
N
FS
Система нормальных уравнений будет иметь вид:
N
11
k
1
+ N
12
k
2
+ N
13
k
3
+ w
1
= 0
N
22
k
2
+ N
23
k
3
+ w
2
= 0
N
23
k
3
+ w
3
= 0
9.4 Оценка точности в коррелатном способе уравнивания
9.4.1 Определение средней квадратической погрешности единицы веса произво
дится
по формуле:
[
]
[
]
r
pv
kn
pv
22
=
−
=µ
где п – число измеренных элементов;
k – число необходимых неизвестных;
r – число избыточных измерений.

63
rkn
m
2)(2
µ
µ
µ
=
−
=
Величина [pv
2
] может быть найдена различными путями:
1. определив поправки v
i
в измеренные величины, вычислим
[
]
∑
=
22
ii
vppv
2. по формуле:
-[pv
2
] = w
1
k
1
+ w
2
k
2
+ w
3
k
3
3. по схеме решения системы нормальных уравнений коррелат:
9.4.2 Вычисление веса функции в коррелатном способе уравнивания. Для оценки точн
о-
сти любой функции необходим представить ее в виде функции результатов измер
ений, а з
а-
тем применить формулу:
∑
=
⋅
∂
∂
=
n
i
iiy
Px
y
P
1
2
11
Пусть дана функция уравненных значений измеренных величин:
y = F (x
1
*, x
2
*, …, x
n
*).
Учитывая, что х
i
* = x
i
+ v
i
получим:
∑ ∑
+=
∂
∂
+=
n
iii
i
n
vFxFv
x
F
xxxFy
1
21
)()...,,,(
Добавив это уравнение к исходной системе, получим новую систему уравнений:
(A Q A
T
) R + L = 0
L R + A Q F =
F
P
1
где L
i
= [q a
i
F]
A Q F = [q F F] = N
(r+1)(r+1)
После исключения k неизвестных получим:
N
(r)
(r+1)(r+1)
=
F
P
1
или
)1(
)1(
)1(
)1(
2
)1(
22
)1(
2
1
11
1
...][
1
−
−
−
−−−−=
r
r
r
rr
r
r
F
L
N
L
L
N
L
L
N
L
qFF
P
64
Практически, для вычисления
F
P
1
необходимо в таблице коэффициентов ввести допо
л-
нительный столбец
F и вписать в него все коэффициенты F
i
=
i
x
F
∂
∂
. Затем вычислить [pa
1
F
],
[
pa
2
F], …, [pa
r
F], [pFF]. При решении нормальных уравнений с этим столб
цом производятся
те же операции, что и со столбцами
W. В итоге после исключения всех неизвестных корре
лат
k
вычислим величину обратного веса.
Легко убедится, что вес любой функции F после уравнивания повышается, т.к. вес зн
а-
чения произведений эллимационных строк в графе
L на вышестоящие числа всегда отриц
а-
тельны, т.е.
)1(
)1(
)1(
)1(
2
)1(
22
)1(
2
1
11
1
...][
1
−
−
−
−−−−=
r
r
r
rr
r
r
F
L
N
L
L
N
L
L
N
L
qFF
P
