Лиман С.А., Радов С.Г. Математическая обработка маркшейдерско-геодезических измерений
Подождите немного. Документ загружается.


11
[
]
n
2
∆
=σ
;
• средняя погрешность:
[ ]
σ8,0
1
≈∆=Θ
n
;
• вероятная погрешность r – значение случайной погрешности, по отношению к к
о-
торому равновероятно появление
большей или меньшей погрешности:
r = 0,7 σ;
• относительная погрешность (применяется для линейных измерений):
L
абс
отн
∆
=∆
;
• средняя квадратическая погрешность – определяется не по всей генеральной сов
о-
купности измерений, когда
п→∞, а по конкретной выборке при фиксированном п:
[
]
n
m
2
∆
=
формула Гаусса;
Это эмпирическое значение стандарта – при п→∞ m→σ;
• предельная погрешность:
∆
пр
= t σ или ∆
пр
= t m
∆
пр
= 2 m с вероятностью 0,95
∆
пр
= 3 т с вероятностью 0,997;
Т.е., если при измерении углов с m
β
= 5” выбрана ∆
пр
= 2 m = 10”, то все резуль
таты
измерений с погрешностью
∆>∆
пр
отбраковываются и не принимаются в дальнейшую обр
а-
ботку. Для ответственных измерений принимается
∆
пр
= 2 m, для менее ответственных - ∆
пр
=
3
m.
2.5 Формула Бесселя для вычисления средней квадратической по-
грешности
Формула Гаусса может применяться в случаях, когда известны истинные погреш
ности
∆
измеряемых величин Х. В большинстве случаев ис
тинное значение измеряемых величин
нам неизвестно, поэтому неизвестны и истинные значения погрешностей изм
ерений ∆.
Пусть величина Х многократно и равноточно измерена n раз. Тогда:

12
∆=−
∆=−
∆
=
−
nn
Xl
Xl
X
l
..................
22
11
1
Вычислим среднее арифметическое из всех результатов измерений
[
]
n
l
n
lll
L
n
=
+
+
+
=
...
21
Обозначим отклонения результатов измерений l
i
от их среднего арифметического зн
а-
чения
L через v
i
. Тогда
=−
=−
=−
nn
vLl
vLl
vLl
................
22
11
2
Вычтем почленно 2 из 1 (например, (l
1
– X) - (l
1
– L) = ∆
1
– v
1
). Тогда:
−∆=−
−∆=−
−∆=−
nn
vXL
vXL
vXL
.........................
22
11
3
При большом числе измерений L – X → некоторая малая величина ε, которая стреми
т-
ся к нулю при
п→∞ (свойство компенсации случайных погрешностей). Обозначим L – X =
ε
Тогда
−=∆
−=∆
−=∆
ε
ε
ε
nn
nn
v
v
v
................
11
4
Сложим квадраты ∆
I
, т.е.
[
]
[
]
222
][2 εε ⋅+⋅⋅+=∆ nvv
. 5
Сумма v равна нулю, т.к. из 2 получаем
[
]
[
]
vLnl =⋅−
, но поскольку
[
]
nlL /=
, след
о-
вательно
[]
[
]
[]
0==− v
n
l
nl
.
Поэтому при любом числе измерений
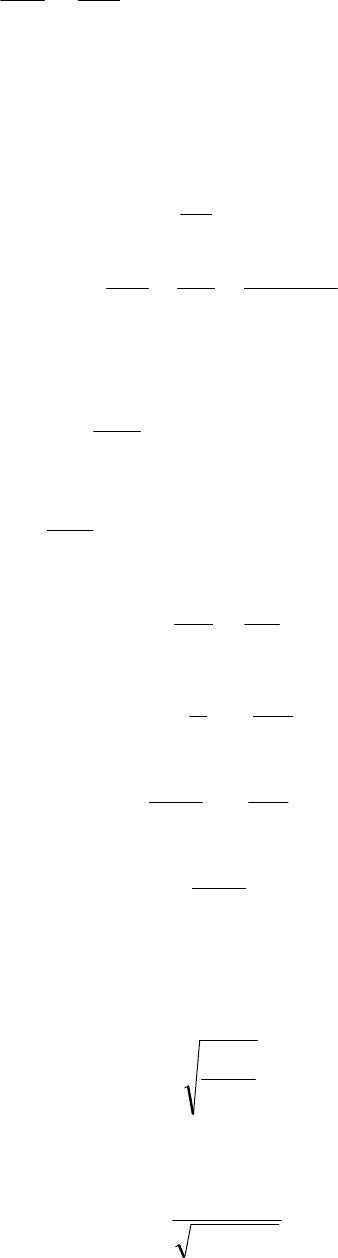
13
[
]
[
]
2
2
2
ε
⋅
+
=
∆
n
v
.
6
Или
[
]
[
]
2
22
ε+=
∆
n
v
n
. 7
Для того, чтобы найти ε
2
сложим уравнения 4.
[
]
[
]
[]
[]
[]
[ ]
[ ]
22
2
2
2
2
2
n
n
n
n
n
nv
ji
∆∆⋅
+
∆
=
∆
=
=
∆
⋅=∆
⋅
+
=
∆
ε
ε
ε
ε
.
Или, учитывая свойство компенсации
[
]
2
2
2
n
∆
=ε
. 8
Подставим 8 в 7 и заменив
[
]
2
2
m
n
=
∆
получим
[
]
n
m
n
v
m
22
2
+=
.
[
]
[ ]
[ ]
1
1
1
1
2
2
2
2
2
2
−
=
=
−
=
−
n
v
m
n
v
n
n
m
n
v
n
m
.
Формула Бесселя для вычисления средней квадратической погрешности измере
ний
имеет вид:
[
]
1
2
−
=
n
v
m
.
А средняя квадратическая погрешность определения т определяется по формуле
)1(2 −
=
n
m
m
m
.

14
2.6 Прин
цип арифмети
ческой середины
Пусть в результате равноточных измерений величины Х получены результаты l
1
, l
2
, …,
n
. Необходимо найти наиболее достоверное значение измеряемой величины и оце
нить его
точность.
Обозначим наиболее достоверное значение измеряемой величины через L и найдем о
т-
клонения результатов измерений
l
i
от L
v
i
= l
i
- L
Найдем
[
]
∑
−=
n
i
Ll
nn
v
1
)(
1
Определим L при условии, что
[
]
0lim ⇒
∞→
n
v
n
(свойство компенсации случайных погре
ш-
ностей). Тогда
[
]
n
l
L =
Используя свойство рассеивания случайных погрешностей найдем вероятнейшее зн
а-
чение
L при условии, что [v
2
] = min.
∑ ∑
−==
n
i
LlvF
1
22
)(
Возьмем производную от F по L и приравняем ее к нулю.
∑
∑
=−
=−⋅−=
n
n
Ll
LlF
1
1
1
1
0)(
0)(2'
Следовательно
[]
n
l
L
Lnl
i
n
=
=⋅−
∑
0
1
1
Таким образом, для ряда многократных измерений среднее арифметическое из всех р
е-
зультатов измерений является наиболее достоверным
значением измеряемой ве
личины или
вероятнейшим
значением.
Средняя квадратическая погрешность вероятнейшего значения вычисляется по форм
у-
ле:

15
n
m
M
L
=
2.7 Точечная и интервальная оценка измерений
При многократных равноточных измерениях одной величины точечная оценка измер
е-
ний сводится к вычислению:
а) вероятнейшего значения L;
б) средней квадратической погрешности измерений т;
в) средней квадратической погрешности вероятнейшего значения измеряемой велич
и-
ны
М
т
.
Точечная оценка измерений величины не характеризует истинное ее значение, а лишь
стремится к нему при неограниченном увеличении числа измерений. В известной степени
этот пробел заполняет
интервальная оцен
ка, которая с заданной доверительной вероятностью
устанавливает инте
рвал, внутри которого находится истинное значение измеряемой велич
и-
ны. Для определения интервала используется предельная погре
шность ∆
пр
.
L - ∆
пр
≤ X ≤ L + ∆
пр
,
где Х – истинное значение измеряемой величины;
L – вероятнейшее значение измеряемой величины.
Предельная погрешность ∆
пр
для среднего арифметического значения L определя
ется
исходя из свойства ограниченности случайных вел
ичин. В нашем случае
∆
пр
= t·M.
Коэффициент t зависит от принятой доверительной вероятности р и от числа избыто
ч-
ных измерений
k. Числа t, k, p связаны математической зависимостью, которую называют з
а-
коном Стьюдента.
Таблица 2.1 – Закон Стьюдента
р
N
0,95 0,9545 0,99 0,9973
2
3
4
5
10
20
∞
4,30
3,18
2,78
2,57
2,23
2,08
-
4,52
3,31
2,87
2,65
2,28
2,13
2,00
9,92
5,84
4,61
4,04
3,17
2,85
-
18,5
9,2
6,63
5,5
3,96
3,42
3,00
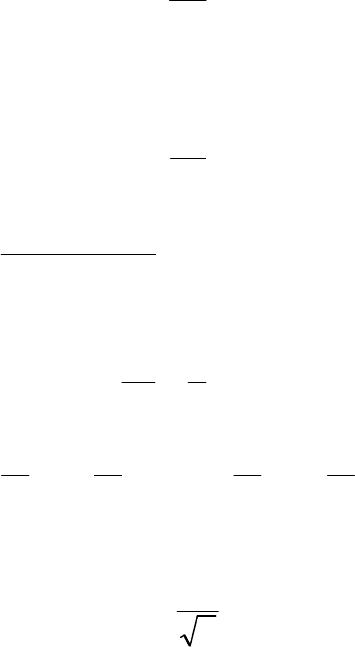
16
2
.8 Средняя квадратическая погрешность функции измеренных вел
и
чин
Определяемая величина часто является функцией некоторых измере
нных величин.
Пусть задана функция
у = f (x
i
). Необходимо найти т
у
при известных значениях т
хi
.
Найдем приращение функции ∆y, разложив функцию в ряд Тейлора и ограничив
шись
членами первого порядка:
∑
∆⋅
∂
∂
=∆
n
i
i
x
x
f
y
1
.
Переходя к средней квадратической погрешности имеем
∑
∂
∂
=
n
xi
i
y
m
x
f
m
1
2
2
2
Например:
lll
n
mmmm
n
lll
L
⇒===
+
+
+
=
ln21
21
...
...
.
nl
L
i
1
=
∂
∂
.
2
2
2
ln
2
2
2
2
2
1
2
2
1
...
11
lllL
m
n
n
m
n
m
n
m
n
m =+++=
.
Следовательно
n
m
m
l
L
=
.
2.9 Обработка двойных равноточных измерений
Сущность двойных измерений заключается в том, что множество однородных ве
личин
измеряются дважды. Например, длины линий теод
о
литного хода измеряются в прямом и в
обратном направлениях.
Пусть даны результаты двух рядов равноточных измерений множества однород
ных
величин
l
1
’ и l
1
”, l
2
’ и l
2
”, …, l
n
’ и l
n
”. Разности двойных измерений будут равны: d
1
= l
1
’ – l
1
”,
d
2
= l
2
’ – l
2
”, …, d
n
= l
n
’ – l
n
”.
Если бы все измерения были безошибочными, то эти разности равнялись бы ну
лю.
Следовательно, разности двойных измерений можно рассматривать как сл
учайные истинные
погрешности. Тогда по формуле Гаусса средняя квадратическая погрешность разности дво
й-
ных измерений будет равна

17
n
dd
m
d
]
[
=
.
Но m
2
d
= m
2
l’
+ m
2
l”
= 2m
2
где т – средняя квадратическая погрешность отдельного измерения (m = m
l’
= m
l”
)
.
Отсюда
n
ddm
m
d
2
][
2
==
.
Если [d] ≠ 0, то при большом п (более 30) в результатах измерений имеется системат
и-
ческая погрешность
n
d
d
i
][
0
=
.
Случайная составляющая погрешностей разностей двойных измерений вычисля
ется по
формуле
v
i
= d
i
– d
0.
Тогда по формуле Бесселя имеем
)1(2
][
2
1
][
2
2
−
==
−
=
n
vm
m
n
v
m
d
d
.
3 НЕРАВНОТОЧНЫЕ ИЗМЕРЕНИЯ
Рассмотренные ранее методы обработки и анализа результатов измерений предпол
а-
гают, что все измерения являются равноточными. Их р
езультаты являются простой случайно
й
выборкой из бесконечной генеральной совокупности всех возможных резул
ь
татов измерений
при постоянных условиях.
Строго говоря, равноточных измерений вообще не бывает, т.к. повторный ряд измер
е-
ний, полученный, казалось бы, в тех же условиях, в действитель
ности будет простой случа
й-
ной выборкой, но уже из другой бесконечной генерал
ь
ной совокупности. Поэтому деление
измерений на равноточные и неравноточные несет условный характер.
Однако измерения одной и той же величины инструментами разной точности, разным
числом приемов, при различных внешних условиях и различным образом сгру
п
пированные
явно выполнены с разной точн
остью, т.е. неравноточны.
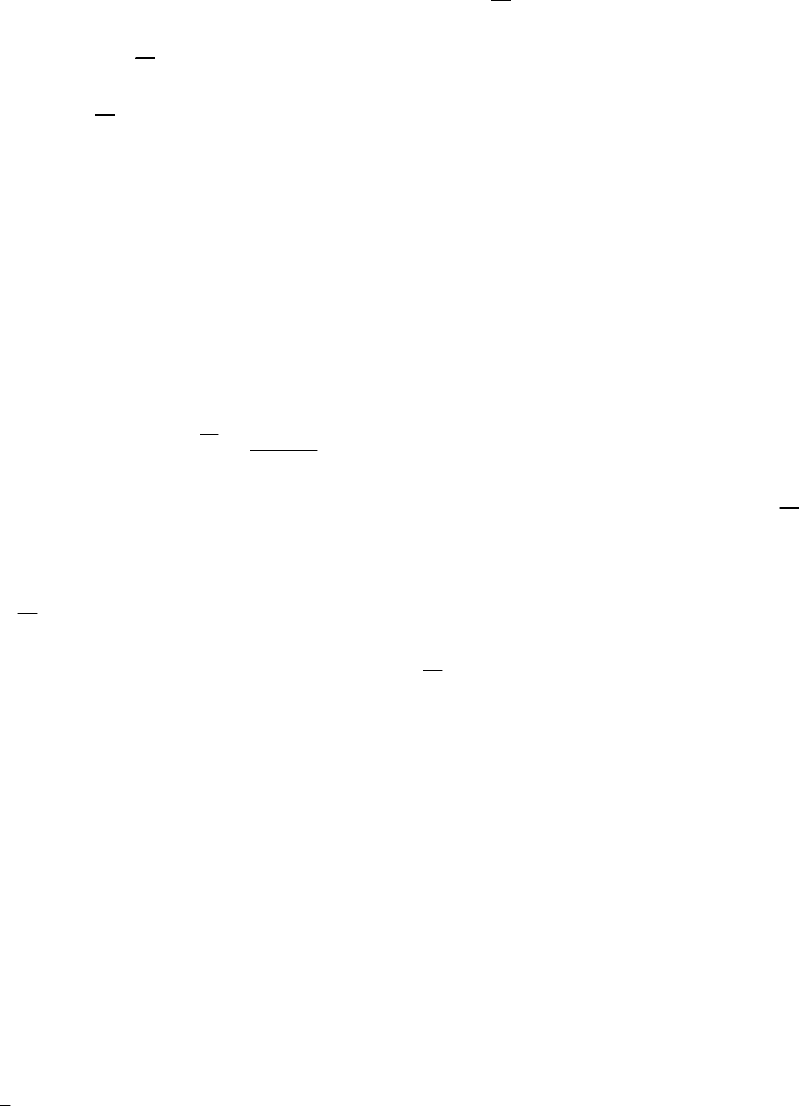
18
3.1 Вероятнейшее значение многократно
и неравноточно измеренной вел
и-
чины
Пусть величина Х измерена многократно и неравноточно. При этом получены резул
ь-
таты
х
1
, х
2
, …, х
п
со средними квадратическими погрешностями т
1
, т
2
, …, т
п
. Необходимо о
п-
ределить вероятнейшее значение этих неравноточных измерений
Х
.
Выразим искомую величину
Х
в виде линейной функции
Х
= k
1
x
1
+ k
2
x
2
+ … + k
n
x
n
,
где k
i
= f (m
i
) – функции средней квадратической погрешности измерений и связа
ны
условием k
1
+ k
2
+ … + k
n
= 1.
Необходимость этих условий вытекает из следующих соображений:
1. равноточные измерения являются частным случаем неравноточных. При т
1
= т
2
=
… = т
п
и k
1
= k
2
= … = k
n
имеем
п
Х
Х
i
∑
=
.
2. Если все результаты измерений случайно окажутся равными между собой, то
Х
=
Х
.
Х
= Х (k
1
+ k
2
+ … + k
n
) = X, т.к. ∑ k
i
= 1.
Величины k
i
найдем при условии, чтобы значение
Х
было получено с наиболь
шей
точностью. Принимая
x
i
независимым, получаем:
т
2
Х
= k
2
1
т
2
1
+ k
2
2
т
2
2
+ … + k
2
n
т
2
n
.
Тогда задача сводится к отысканию условного экстремума: требуется найти ми
нимум
функции
т
2
Х
= f (k
1
, k
2
, …, k
n
) = т
2
1
k
2
1
+ т
2
2
k
2
2
+ … + т
2
n
k
2
n
.
при ∑ k
i
– 1 = 0.
Следовательно
2
2
1
1
1
1
2222
1
1
222
1
n
n
i
i
n
i
iinn
n
i
ii
X
mkmkmkmkm
−+=+=
∑∑∑
−
=
−
=
−
=
.
Возьмем частные производные по k
i
(i = 1, n-1) и приравняем к нулю. Получим:
0122
2
2
1
1
2
=
−−
∑
−
=
n
n
i
iii
mkmk
.
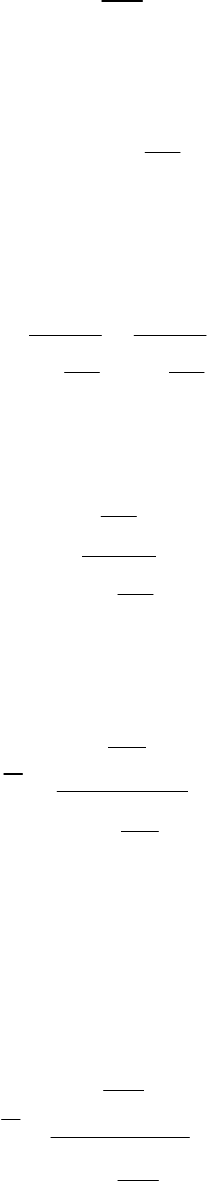
19
2
2
nnii
m
k
m
k
=
.
Следовательно, величины k
i
должны быть обратно пропорциональны т
2
i
, т.е.
2
i
i
m
k
λ
=
.
Возьмем сумму этих равенств
∑∑
==
=
n
i
i
n
i
i
m
k
1
2
1
1
λ
.
Тогда
∑∑
∑
==
=
==
n
i
i
n
i
i
n
i
i
mm
k
1
2
1
2
1
1
1
1
λ
.
Следовательно
∑
=
=
n
i
i
i
i
m
m
k
1
2
2
1
1
.
Тогда искомое вероятнейшее значение будет определяться по формуле
∑
∑
=
=
=
n
i
i
n
i
i
i
m
x
m
X
1
2
1
2
1
1
.
Поставленная задача решена. Но для удобства вычислений введем безразмерный к
о-
эффициент
µ
2
, на который умножим числитель и знаменатель (µ
2
выбираем с таким усл
овием,
чтобы
µ
2
/т
2
i
≈ 1 или близким к 1).
∑
∑
=
=
=
n
i
i
n
i
i
i
m
x
m
X
1
2
2
1
2
2
µ
µ
.
Величину µ
2
/т
2
i
называют весами соответствующих результатов измерений и обозн
а-
чают через
Р
i
, т.е.
P
i
= µ
2
/т
2
i.

20
Тогда
∑
∑
=
=
=
n
i
i
n
i
ii
p
xp
X
1
1
.
Величина
Х
называется весовым средним или общей арифметической серединой.
3.2 Веса измерений и средняя квадратическая погрешность единицы веса
В геодезической практике к представлению о весе часто приходят косвенным пу
тем.
Например, считая вес пропорциональным числу приемов измере
ний и обратно пропорци
о-
нальным длине нивелирных ходов. Т.е. надежность результата тем выше, чем большим чи
с-
лом приемов в
ыполнены измерения или чес короче длина нивелирного хода.
Выше было введено понятие веса как величины
2
2
i
i
m
P
µ
=
,
где µ
2
– безразмерный коэффициент.
Таким образом, вес представляет собой надежность результатов измерений, выраже
н-
ную числом. Вес результатов измерений является положительным числом, обратно пропо
р-
циональным квадратам их средних квадратических погрешностей. Если
Р = 1, то численно
µ
= т
. Поэтому величину µ называют средней квадратической погрешностью единицы веса.
Для функции измеренных величин вес P
F
функции F при известной ее средней квадр
а-
тической погрешности
m
F
вычисляется по формуле:
2
2
F
F
m
P
µ
=
.
При вычислениях с весами в практике возникают два типа задач:
1. установление весов неравноточных или разнородных результатов с целью их с
о-
вместной обработки;
2. отыскание весов функций неравноточных или разнородных результатов для вычи
с-
ления затем средней квадра
тической погрешности m
F
функции F
, т.е. для оценки точности
этих функций.
При обработке ряда неравноточных измерений средняя квадратическая погреш
ность
единицы веса вычисляется по формулам:
