Лекции - Теория марковских случайных процессов
Подождите немного. Документ загружается.

Теория марковских случайных процессов
1. Понятие случайного процесса.
Случайным процессом называется множество или семейство случайных величин,
значения которых индексируются временным параметром. Например, число студентов в
аудитории, атмосферное давление или температура в этой аудитории как функции
времени являются случайными процессами.
Случайные процессы находят широкое применение при изучении сложных
стохастических систем как адекватные математические модели процесса
функционирования таких систем.
Основными понятиями для случайных процессов являются понятия состояния
процесса и перехода его из одного состояния в другое.
Значения переменных, которые описывают случайный процесс, в данный момент
времени называются состоянием случайного процесса. Случайный процесс совершает
переход из одного состояния в другое, если значения переменных, задающих одно
состояние, изменяются на значения, которые определяют другое состояние.
Число возможных состояний (пространство состояний) случайного процесса
может быть конечным или бесконечным. Если число возможных состояний конечно или
счетно (всем возможным состояниям могут быть присвоены порядковые номера), то
случайный процесс называется процессом с дискретными состояниями. Например, число
покупателей в магазине, число клиентов в банке в течение дня описываются случайными
процессами с дискретными состояниями.
Если переменные, описывающие случайный процесс, могут принимать любые
значения из конечного или бесконечного непрерывного интервала, а, значит, число
состояний несчетно, то случайный процесс называется процессом с непрерывными
состояниями. Например, температура воздуха в течение суток является случайным
процессом с непрерывными состояниями.
Для случайных процессов с дискретными состояниями характерны
скачкообразные переходы из одного состояния в другое, тогда, как в процессах с
непрерывными состояниями переходы являются плавными. Далее будем рассматривать
только процессы с дискретными состояниями, которых часто называют цепями.
Обозначим через g(t) случайный процесс с дискретными состояниями, а
возможные значения g(t), т.е. возможные состояния цепи, - через символы E
0
, E
1
, E
2
, … .
Иногда для обозначения дискретных состояний используют числа 0, 1, 2,... из
натурального ряда.
Случайный процесс g(t) называется процессом с дискретным временем, если
переходы процесса из состояния в состояние возможны только в строго определенные,
заранее фиксированные моменты времени t
0
, t
1
, t
2
, …. Если переход процесса из состояния
в состояние возможен в любой, заранее неизвестный момент времени, то случайный
процесс называется процессом с непрерывным временем. В первом случае, очевидно, что
интервалы времени между переходами являются детерминированными, а во втором -
случайными величинами.
Процесс с дискретным временем имеет место либо, когда структура системы,
которая описывается этим процессом, такова, что ее состояния могут изменяться только
в заранее определенные моменты времени, либо когда предполагается, что для описания
процесса (системы) достаточно знать состояния в определенные моменты времени. Тогда
эти моменты можно пронумеровать и говорить о состоянии E
i
в момент времени t
i
.
Случайные процессы с дискретными состояниями могут изображаться в виде
графа переходов (или состояний), в котором вершины соответствуют состояниям, а
ориентированные дуги - переходам из одного состояния в другое. Если из состояния E
i
возможен переход только в одно состояние E
j
, то этот факт на графе переходов
1

E
j
E
j
отражается дугой, направленной из вершины E
i
в вершину E
j
(рис.1,а). Переходы из
одного состояния в несколько других состояний и из нескольких состояний в одно
состояние отражается на графе переходов, как показано на рис.1,б и 1,в.
а) б) в)
E
i
E
j
E
i
E
k
E
k
E
i
E
m
E
m
Рис.1. Фрагменты графа переходов.
2. Понятие марковского случайного процесса.
Особое место среди случайных процессов занимают так называемые марковские
случайные процессы, впервые описанные А.А. Марковым в 1907г. Случайный процесс
называется марковским, если вероятность любого его состояния в будущем зависит
только от состояния в настоящем и не зависит от того, каким образом и когда процесс
пришел в текущее состояние. Аналитически сказанное может быть записано в виде:
Pr{g(t
n+1
)=E
n+1
|g(t
0
)=E
0
, g(t
1
)=E
1
, …, g(t
n
)=E
n
}=
=Pr{g(t
n+1
)=E
n+1
|g(t
n
)=E
n
},
где t
1
<t
2
< … <t
n
<t
n+1
, а E
n
- текущее состояние. Иными словами, в марковских случайных
процессах влияние (воздействие) всей предыстории процесса на его будущее полностью
сосредоточено в текущем состоянии процесса. Это свойство называется свойством
отсутствия последействия или применительно к случайным процессам марковским
свойством.
Свойство отсутствия последействия накладывает существенные ограничения на
распределение времени пребывания марковского процесса в том или ином состоянии.
Так, в случае цепи Маркова с непрерывным временем время пребывания в данном
состоянии должно быть распределено по экспоненциальному, а в случае дискретной цепи
Маркова - по геометрическому, законам распределения, которые являются
единственными, соответственно, непрерывным и дискретным распределениями без
последействия. Только при таких ограничениях на времена пребывания процесса в
состояниях гарантировано выполнение марковского свойства.
Рассмотрим марковский случайный процесс g(t) с конечным числом состояний E
0
,
E
1
, …, E
n
. Обозначим через P
i
(t) вероятность того, что случайный процесс в момент
времени t находится в состоянии E
i
:
P
i
= Pr{g{t} = E
i
}, i = 0,n.
Очевидно, что в любой момент времени t процесс находится в одном из n+1
возможных состояний, т.е. события g{t}=E
i
, i = 0,n заключающиеся в том, что в момент
времени t процесс находится в состояниях E
0
, E
1
,…, E
n
, образуют полную группу
несовместных событий. Отсюда следует, что в любой момент времени t выполняется
условие:
n
i
i
tP
0
)(
1,
2
(1)
(2)
(3)
…
…
…
…
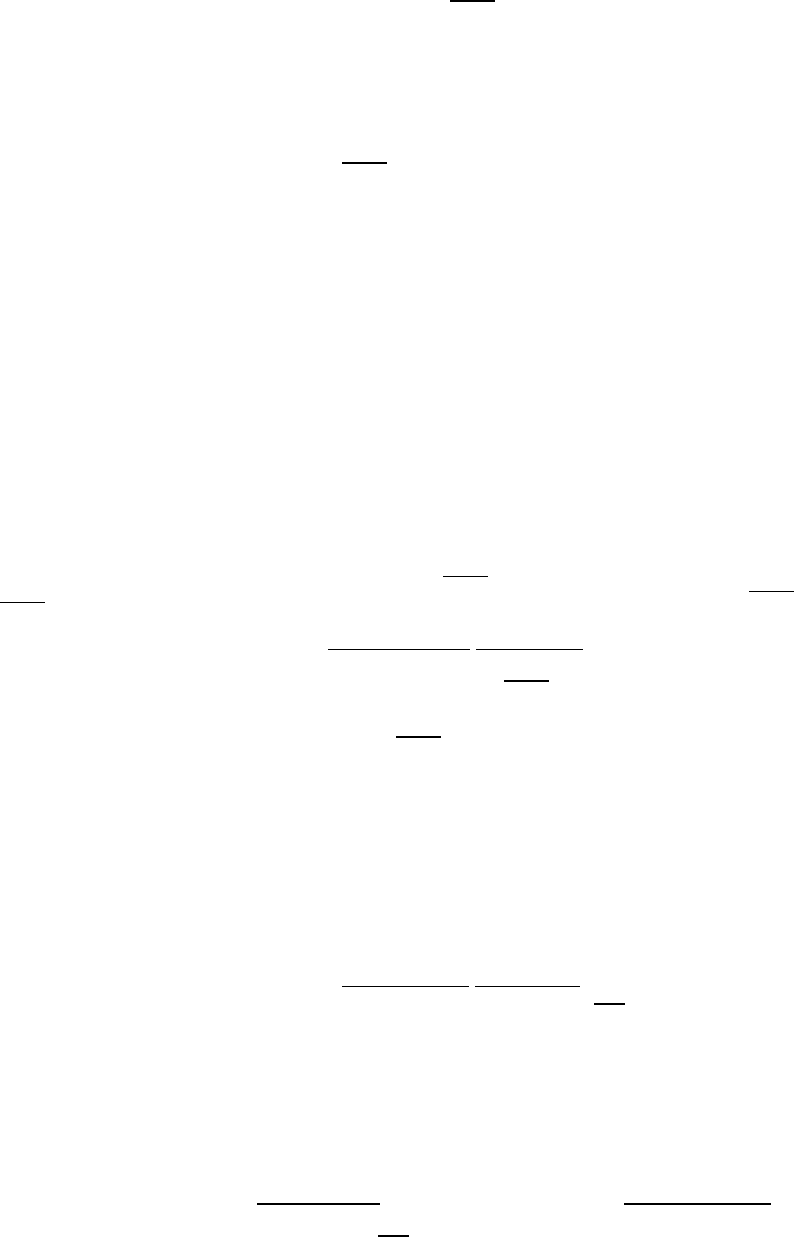
которое называется нормировочным.
Совокупность вероятностей P
i
(t), i=0,n, может быть представлена вектором,
называемым вектором состояний, с числом компонент, равным числу возможных
состояний процесса:
P(t)={P
0
(t), P
1
(t), …, P
n
(t)}.
Главная задача изучения марковских случайных процессов заключается в
определении вероятностей P
i
(t), i = 0,n, нахождения процесса в любой момент времени t в
том или ином состоянии, что дает полную информацию о случайном процессе. Для
решения данной задачи необходимо:
1) указать в каком состоянии находится процесс в начальный момент времени;
2) описать переходы между состояниями.
Состояние процесса в начальный момент времени t=0 задается вектором
начальных вероятностей
P(0)={P
0
(0), P
1
(0), …, P
n
(0)}.
Описание переходов между состояниями зависит от того, каким (с дискретным или
с непрерывным временем) является изучаемый марковский случайный процесс. Этот
вопрос будет рассматриваться в следующих параграфах.
Очень часто при изучении марковских случайных процессов достаточно
определить не вероятности P
0
(t), P
1
(t), …, P
n
(t) в любой момент времени t, а их
предельные значения (если они существуют) при
t
.
Если при
t
вероятности P
i
(t), i=0,n, стремятся к предельным значениям P
i
,
i=0,n, не зависящим от распределения начальных вероятностей P
i
(0), i=0,n, то говорят,
что случайный процесс обладает эргодическим свойством. Таким образом, для процессов,
обладающих эргодическим свойством, существуют пределы
ii
t
PtP
)(lim
, i=0,n.
Предельные вероятности P
i
, i=0,n, часто называют вероятностями состояний
равновесия или стационарными вероятностями.
3. Марковские процессы с дискретным временем.
Как было определено ранее, для случайных процессов с дискретным временем
изменения состояний возможны только в определенные моменты времени, и эти моменты
обозначим через t
0
, t
1
, t
2
, … . В случае дискретной цепи Маркова для описания переходов
между состояниями используются вероятности переходов, определяемые как
p
ij
(t
k
)=Pr{g(t
k+1
)=E
j
|g(t
k
)=E
i
}, i,j=0,n.
Вероятность перехода (за один шаг) p
ij
(t
k
) задет вероятность того, что случайный
процесс на следующем (k+1)-ом шаге перехода (в момент времени t
k+1
) окажется в
состоянии E
j
при условии, что на текущем k-ом шаге (в момент времени t
k
) он находится в
состоянии E
i
.
Если вероятности переходов p
ij
(t
k
) не зависят от момента времени t
k
, т.е. p
ij
(t
k
)=p
ij
, то
цепь Маркова называется однородной, в противном случае - неоднородной. Далее будем
рассматривать только однородные цепи Маркова.
Вероятности переходов p
ij
, i,j=0,n, обычно задаются в виде квадратной матрицы T
размерности (n+1)(n+1):
3
(4)

nnnnn
n
n
n
pppE
pppE
pppE
EEE
10
111101
001000
10
элементы которой удовлетворяются условиям:
n
j
ij
p
0
1
, i=0,n;
10
ij
p
, i,j=0,n.
Условие (5) означает, что в любой момент времени t
0
, t
1
, t
2
, … процесс обязательно
(с вероятностью 1) перейдет из состояния E
i
в какое-либо другое состояние E
0
, E
1
,
, E
n
,
причем не исключается возможность перехода в то же самое состояние.
Матрица, удовлетворяющая условиям (5) и (6), называется стохастической.
Поскольку элементами стохастической матрицы Т являются вероятности переходов p
ij
, то
эта матрица называется матрицей вероятностей переходов.
Наряду с вероятностями переходов p
ij
за один шаг, определим вероятности
переходов за m шагов в виде
})(|)(Pr{
)(
ikjmk
m
ij
EtgEtgp
, m=1, 2, …
Здесь
)(m
ij
p
задет вероятность того, что через m переходов случайный процесс
окажется в состоянии E
j
при условии, что на текущем шаге он находится в состоянии E
i
. В
силу однородности марковской цепи вероятности
)(m
ij
p
, i,j=0,n, не зависят от текущего
времени t
k
.
Используя марковское свойство, легко вывести следующую формулу для
вычисления вероятностей
)(m
ij
p
:
n
k
kj
m
ik
m
ij
ppp
0
)1()(
, m=2, 3, …
Это равенство означает, что для попадания из состояния E
i
в состояние E
j
за m
шагов необходимо сначала попасть из состояния E
i
в некоторое состояние E
k
за m-1
шагов, а затем за один шаг перейти из E
k
в E
j
. Вероятность этих двух независимых
событий (они независимы в силу марковского свойства) равна произведению
вероятностей каждого из них, и, если просуммировать эти произведения по всем
возможным промежуточным состояниям E
k
, то получится вероятность
)(m
ij
p
.
Цепь Маркова называется неприводимой, если каждое ее состояние может быть
достигнуто из любого другого состояния, т.е. для каждой пары состояний E
i
и E
j
существует целое число m
0
такое, что
0
)(
0
m
ij
p
. Состояние E
i
называется поглощающим,
если процесс достигнув это состояние, не покидает его. Очевидно, для поглощающего
состояния p
ii
=1. Состояние E
i
называется невозвратным, если случайный процесс после
какого-то числа переходов непременно покидает его.
Вернемся к вопросу определения вероятностей состояний P
i
(t
k
), i=0,n, предполагая,
что начальные вероятности P
i
(t
0
), i=0,n, при t
0
=0 известны.
Используя доводы, аналогичные тем, что были приведены для обоснования
равенства (7), легко определить, что искомые вероятности после первого шага, т.е. на
момент времени t
1
4
(5)
(6)
(7)
,
T=[p
ij
]=

n
j
jiji
pPtP
0
1
)0()(
, i=0,n.
Вероятности состояний после второго шага на момент времени t
2
определяются
аналогично:
n
j
jiji
ptPtP
0
12
)()(
, i=0,n.
В общем случае после k-го шага на момент времени t
k
, k=1, 2,..., вероятности
состояний будут равны
n
j
jikjki
ptPtP
0
1
)()(
, i=0,n.
В векторной форме равенства (8) имеют вид:
P(t
k
)=P(t
k-1
)T.
Если случайный процесс обладает эргодическим свойством, т.е. существуют
пределы
)(lim)(lim
1
ki
t
ki
t
tPtP
kk
, i=0,n, то соответствующие предельные значения
вероятностей состояний P
i
, i=0,n, для стационарного режима определяются из решения
системы уравнений:
n
j
jiji
pPP
0
, i=0,n
или в векторном виде
P=PT
с нормировочным условием
В системе (10) уравнения являются линейно зависимыми и любое из них можно
исключить из нее, а недостающее при этом (для однозначного определения n+1
неизвестных) уравнение составляет условие (11).
Сформулируем теперь правило составления уравнений для стационарных
вероятностей состояний марковского процесса с дискретным временем по графу
переходов. Для каждого состояния уравнение составляется следующим образом. В левой
части уравнения записывается стационарная вероятность рассматриваемого состояния.
Правая часть представляет собой сумму членов, число которых равно числу дуг,
входящих в рассматриваемое состояние. Каждый член представляет собой произведение
вероятности перехода, соответствующей данной дуге, на вероятность состояния, из
которого исходит эта дуга. Сформулированное правило позволяет чисто механически
записывать уравнения для стационарных вероятностей состояний непосредственно по
графу переходов.
Пример. Рассмотрим систему, которая состоит из двух устройств y
1
и y
2
, каждое из
которых может находиться в одном из двух состояний: не работает (обозначим это
состояние через 0) и работает (состояние 1). В определенные моменты времени может
включиться или выключиться только одно устройство. Пусть процесс функционирования
такой системы описывается процессом с дискретным временем. Выделим возможные
состояния процесса (системы):
5
(8)
(9)
(10)
(11)
1
0
n
i
i
P
.
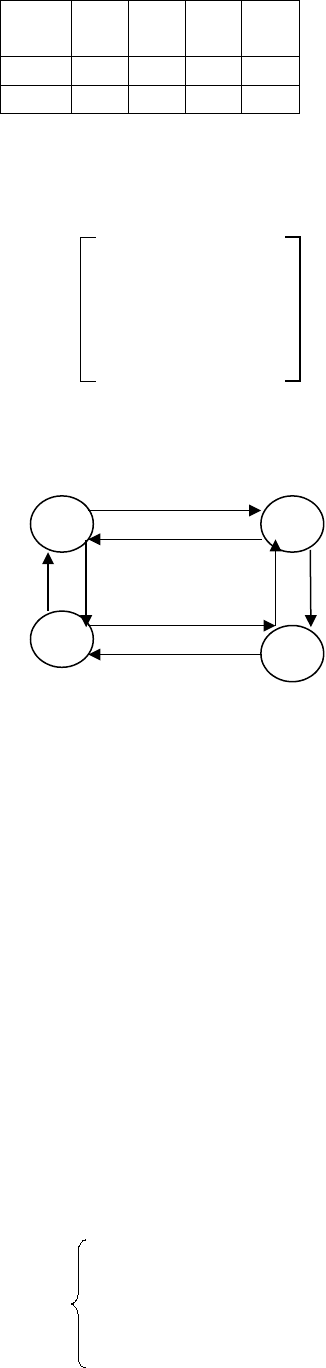
y
1
0 0 1 1
y
2
0 1 0 1
Предположим, что известны вероятности переходов, представленные в виде
матрицы
06.04.00
5.0005.0
5.0005.0
08.02.00
3
2
1
0
3210
E
E
E
E
EEEE
и начальные вероятности P
0
(0)=0,7, P
1
(0)=P
2
(0)=P
3
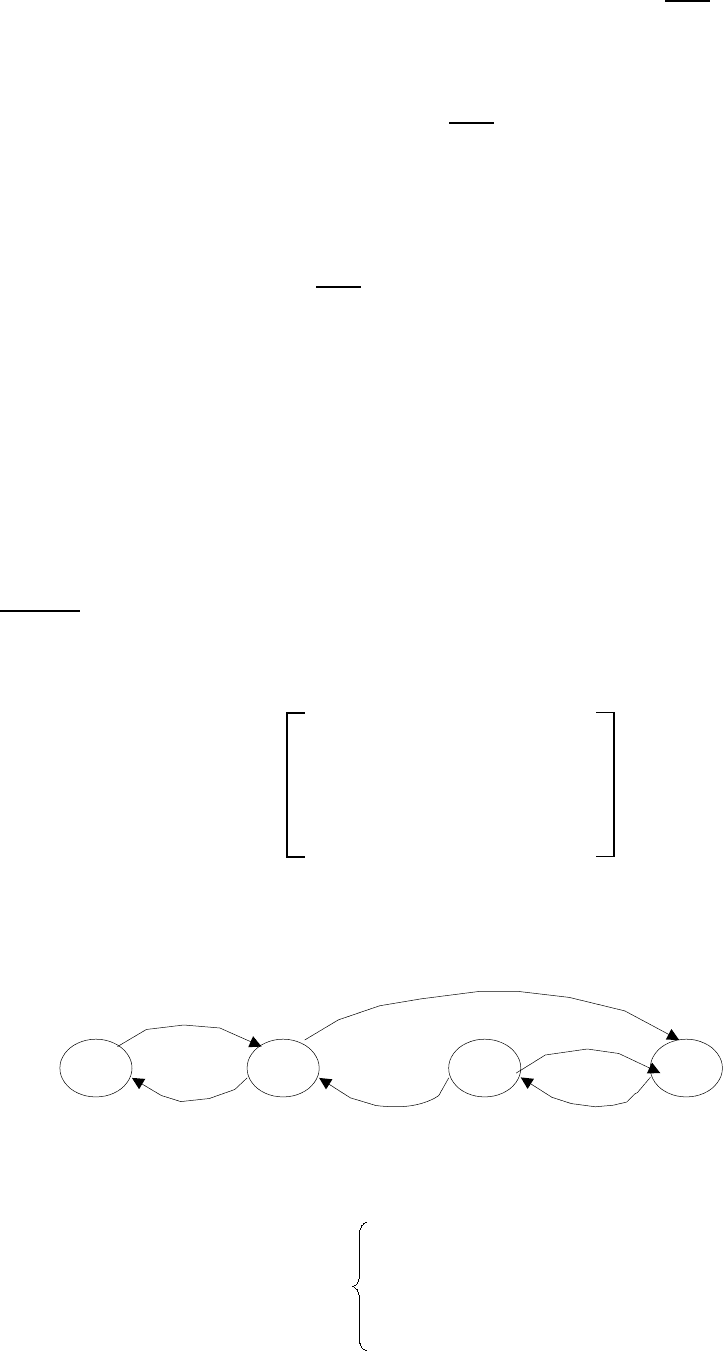
(0)=0,1. Граф переходов для этого
процесса имеет вид, показанный на рис. 2.
Рис. 2. Граф переходов.
Определим вероятности состояний на различные моменты времени. Согласно
формуле (8) вероятности состояний на момент времени t
1
:
P
0
(t
1
) =P
0
(0) p
00
+ P
1
(0) p
10
+P
2
(0) p
20
+ P
3
(0) p
30
=0.1;
P
1
(t
1
) =P
0
(0) p
01
+ P
1
(0) p
11
+P
2
(0) p
21
+ P
3
(0) p
31
=0.18;
P
2
(t
1
) =P
0
(0) p
02
+ P
1
(0) p
12
+P
2
(0) p
22
+ P
3
(0) p
32
=0.62;
P
3
(t
1
) =P
0
(0) p
03
+ P
1
(0) p
13
+P
2
(0) p
23
+ P
3
(0) p
33
=0.1;
на момент времени t
2
:
P
0
(t
2
) = P
0
(t
1
) p
00
+ P
1
(t
1
) p
10
+ P
2
(t
1
) p
20
+ P
3
(t
1
) p
30
=0.4;
P
1
(t
2
) = P
0
(t
1
) p
01
+ P
1
(t
1
) p
11
+ P
2
(t
1
) p
21
+ P
3
(t
1
) p
31
=0.06;
P
2
(t
2
) = P
0
(t
1
) p
02
+ P
1
(t
1
) p
12
+ P
2
(t
1
) p
22
+ P
3
(t
1
) p
32
=0.14;
P
3
(t
2
) = P
0
(t
1
) p
03
+ P
1
(t
1
) p
13
+ P
2
(t
1
) p
23
+ P
3
(t
1
) p
33
=0.4;
и т.д.
Предполагая, что рассматриваемый случайный процесс обладает эргодическим
свойством, что соответствует действительности, определим вероятности состояний для
стационарного режима. Искомые вероятности P
0
, P
1
, P
2
, P
3
могут быть найдены, согласно
равенствам (10) и (11), из системы уравнений:
P
0
= 0.5P
1
+0.5P
2
P
1
= 0.2P
0
+0.4P
3
P
2
= 0.8P
0
+0.6P
3
P
3
= 0.5P
1
+0.5P
2
P
0
+P
1
+P
2
+P
3
=1.
6
0,2
E
0
E
1
E
2
E
3
0,5
0,4 0,50,5 0,8
0,6
0,5
E
i
y
i
E
0
E
1
E
2
E
3
,
T=

Легко проверить, что такую же систему мы получим, если воспользуемся
приведенным выше правилом составления уравнений для стационарных вероятностей по
графу переходов.
Решив систему уравнений, получим: P
0
=0.25; P
1
=0.15; P
2
=0.35; P
3
=0.25.
В заключении вернемся к вопросу о свойстве отсутствия последействия для
марковских цепей с дискретным временем и докажем, что время пребывания в данном
состоянии имеет геометрическое распределение.
Предположим, что процесс только что перешел в состояние E
i
. Он останется в этом
состоянии на следующем шаге с вероятностью p
ii
и с вероятностью 1-p
ii
уйдет из этого
состояния. Если процесс действительно останется в этом состоянии, то вероятность того,
что на следующем, втором, шаге он останется в данном состоянии, по-прежнему равна p
ii
,
а вероятность того, что процесс перейдет в другое состояние, останется равной 1-p
ii
. И так
далее. Более того, благодаря марковскому свойству тот факт, что процесс пребывал в
данном состоянии известное число шагов, никак не сказывается на вероятности остаться
на следующем шаге в этом же состоянии или перейти в некоторое другое состояние. Так
как эти события независимы, то вероятность того, что процесс находился в состоянии E
i
точно m шагов и затем сразу перешел в другое состояние, равна (1-p
ii
)
m
ii
p
, что и задает
геометрическое распределение.
4. Марковские процессы с непрерывным временем.
Для марковских процессов с непрерывным временем, когда переходы из одного
состояния в другое возможны в любой момент времени, вероятность перехода из
состояния E
i
в состояние E
j
точно в момент времени t не может быть задана, поскольку
такая вероятность равна нулю. Вместо этого можно определить вероятность
соответствующего перехода на интервале времени (t, t+t), определяемая как
p
ij
(t, t +t)=Pr
{g (t+t)=E
j
| g (t)=E
i
}, i, j=0,n.
При этом
0),(lim
0
tttp
ij
t
, i, j=0,n.
В случае марковской цепи с непрерывным временем для описания переходов
используются не вероятности переходов, а интенсивности переходов. Интенсивность
перехода из состояния E
i
в состояние E
j
в момент времени t, обозначаемая через q
ij
(t),
определяется следующим образом:
q
ij
(t)=
t
tttp
ij
t
),(
lim
0
, ij; (12)
q
ii
(t)=
t
tttp
ii
t
1),(
lim
0
. (13)
Эти пределы имеют следующую интерпретацию. Если в момент времени t
процесс находится в состоянии E
i
, то вероятность перехода в течение промежутка
времени (t,t+t) в произвольное (отличное от E
i
) состояние задается величиной -q
ii
(t)
t+o(t)
1
. Таким образом, величину -q
ii
(t) можно интерпретировать как интенсивность,
с которой процесс уходит из состояния E
i
. Аналогично, вероятность перехода процесса
в течение времени (t, t+t) из состояния E
i
в состояние E
j
задается величиной
+q
ij
(t)t+o(t) и величину q
ij
(t) можно интерпретировать как интенсивность, с которой
процесс переходит из состояния E
i
в состояние E
j
, при условии, что E
i
- текущее
1
Символ o(t) ("o" малое от t) означает произвольную функцию, которая при
t0, стремится к нулю быстрее, чем t, т.е.
0
)(
lim
0
t
to
t
.
7
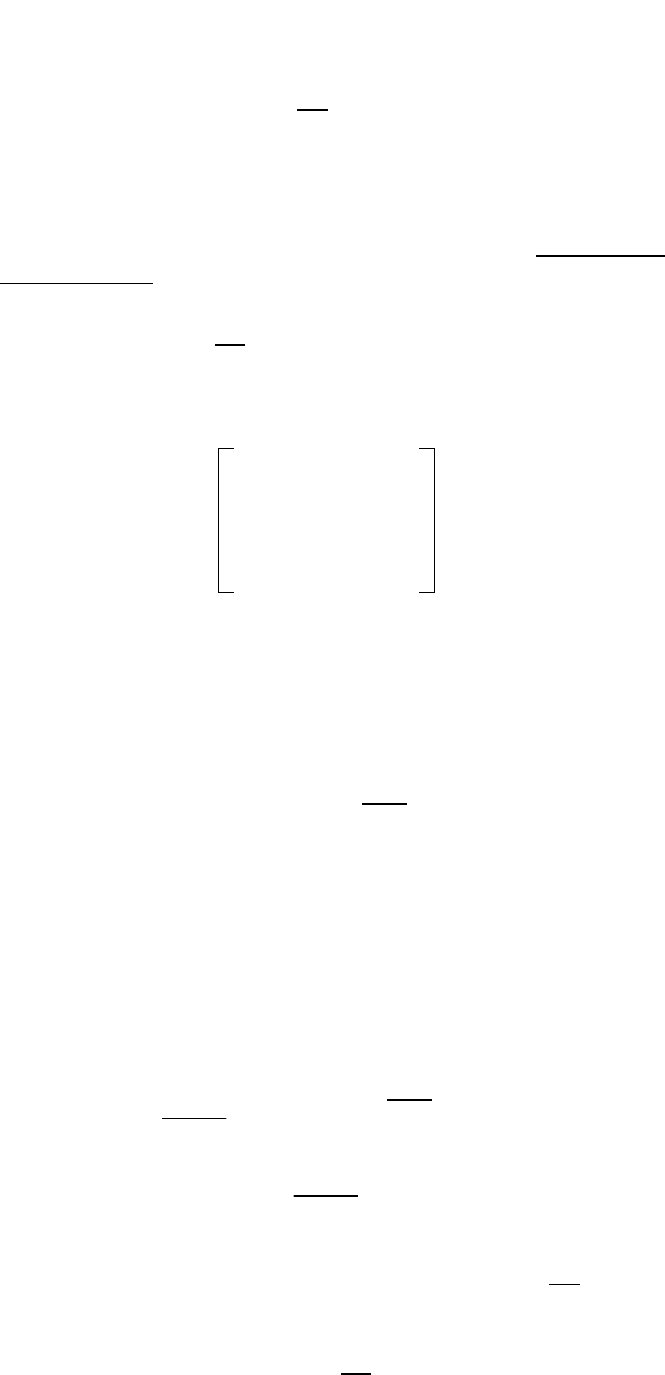
состояние процесса. Так как всегда
n
j
ij
p
0
(t,t+t)=1, то из равенств (12) и (13) следует,
что
n
j
ij
q
0
(t)=0, i=0,n.
Если вероятности переходов p
ij
(t,t+t), а, значит, и интенсивности переходов
q
ij
(t), не зависят от времени t (p
ij
(t,t+t)p
ij
(t) и q
ij
(t) q
ij
), т.е. от того, в какой момент
начинается промежуток t, то марковский процесс называется однородным, в
противном случае - неоднородным.
Далее, рассматривая марковские случайные процессы с непрерывным временем,
будем считать их однородными.
Интенсивности переходов q
ij
,
i,j=0,n, можно задать в виде квадратной матрицы Q
размерности (n+1)(n+1):
nnnnn
n
n
n
qqqE
qqqE
qqqE
EEE
10
111101
001000
10
называемая матрицей интенсивностей переходов. Элементы матрицы переходов Q
удовлетворяют условию (14) (сумма элементов строки равна нулю), и такая матрица
называется дифференциальной.
Рассмотрим теперь задачу определения вероятностей (2) марковского
случайного процесса с непрерывным временем.
Вероятность того, что марковский процесс в момент времени t+t окажется в
состоянии E
i
, определяется как
P
i
(t+t) =
n
j
j
P
0
(t)p
ji
(t), i=0,n.
Действительно, марковский процесс в момент времени t+t окажется в
состоянии E
i
, если он в момент времени t находится в состоянии E
j
(с вероятностью
P
j
(t)) и за промежуток времени t перейдет с вероятностью p
ji
(t) из состояния E
j
в
состояние E
i
. Суммируя произведения вероятностей этих двух независимых событий по
всем возможным состояниям процесса в момент времени t, получим равенство (15).
Если вычесть P
i
(t) от обоих сторон равенства (15), а затем разделить на t и
определить соответствующие пределы при t0, то получим:
ji
n
j
j
i
qtP
dt
tdP
)(
)(
0
, i=0,n
или в векторном виде:
dt
td )(
(16)
Решая данную систему дифференциальных уравнений при заданном
распределении P(0)={P
0
(0), P
1
(0), ..., P
n
(0)} начальных вероятностей с учетом
нормировочного условия (3), можно определить вероятности P
i
(t), i=0,n, состояний
марковского случайного процесса в любой момент времени.
В случае эргодичности марковского случайного процесса существуют
предельные (при t) вероятности состояний P
i
, i=0,n, и они не зависят от начальных
условий и временного параметра. Тогда производные dP
i
(t)/dt=0, i=0,n, и система
8
(14)
(15)
,
Q=[q
ij
]=
P(t)Q.
P
дифференциальных уравнений (16) для стационарного режима превращается в систему
линейных алгебраических уравнений:
0
0
n
j
jij
qP
, i=0,n
или в векторном виде (17)
PQ=0.
Система (17) совместно с нормировочным условием дает единственное решение
для стационарных вероятностей P
i
, i=0,n.
Систему уравнений для вероятностей состояний равновесия марковского
процесса с непрерывным временем можно составить непосредственно по графу
переходов, используя принцип равенства потоков вероятностей, который состоит в
следующем: в состоянии равновесия марковского процесса поток вероятностей в любое
состояние равен потоку вероятностей из этого состояния. При этом под потоком
вероятностей, например, в данное состояние, понимается сумма произведений
интенсивностей переходов в это состояние на вероятности тех состояний, откуда
происходят эти переходы. Принцип равенства применим не только к потоку
вероятностей для отдельных состояний, но и к потоку через любую замкнутую
границу.
Пример. Определим вероятности состояний равновесия марковского случайного
процесса с четырьмя возможными состояниями E
0
, E
1
, E
2
, E
3
и матрицей
интенсивностей переходов
00
)(0
0)(
00
4
3
1
0
4310
E
E
E
E
EEEE
Граф переходов для этого процесса приведен на рис. 3. В диаграмму переходов
не включены петли, ведущие из состояния E
i
, i=0,3, обратно в это же состояние, так
как, согласно (14), члены на главной диагонали матрицы Q не содержат никакой новой
информации: они равны сумме элементов соответствующей строки, взятой со знаком
минус.
Рис. 3. Граф переходов примера.
Система (17) вместе с нормировочным условием для этого примера имеет вид:
-
P
0
+
P
1
=0
P
0
-(
+
)P
1
+
P
2
=0
-(
+
)P
2
+
P
3
=0
P
1
+
P
2
-
P
3
=0
P
0
+P
1
+P
2
+P
3
=1
Первые четыре уравнения полученной системы являются линейно зависимыми,
и любое из них можно исключить из системы, а остальные три уравнения и
9
E
0
E
3
E
1
E
2
μ μ μ
λ
λ
P
0
P
1
P
2
P
3
λ
Q =
.
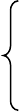
нормировочное условие определяют единственное решение для вероятностей
состояний равновесия. Если
= 2 и
= 1, то P
0
=1/19, P
1
=2/19, P
2
=4/19 и P
3
=12/19.
Применение принципа равенства потоков вероятностей к отдельным состояниям дает
такую же систему уравнений. Так, например, для состояния E
3
P
1
+
P
2
=
P
3
, что
соответствует четвертому уравнению приведенной выше системы.
5. Процессы размножения и гибели.
Процессы размножения и гибели являются частным случаем марковских
случайных процессов, которые тем не менее находят весьма широкое применение при
исследовании дискретных систем со стохастическим характером функционирования.
Процесс размножения и гибели представляет собой марковский случайный процесс, в
котором переходы из состояния E
i
допустимы только в соседние состояния E
i-
1
, E
i
и E
i+1
.
Процесс размножения и гибели является адекватной моделью для описания изменений,
происходящих в объеме биологических популяций. Следуя этой модели, говорят, что
процесс находится в состоянии E
i
, если объем популяции равен i членам. При это
переход из состояния E
i
в состояние E
i+1
соответствует рождению, а переход из E
i
в E
i-1
-
гибели, предполагая, что объем популяции может изменяться не более чем на единицу;
это означает, что для процессов размножения и гибели не допускаются многократные
одновременные рождения и/или гибели.
Дискретные процессы размножения и гибели менее интересны, чем
непрерывные, поэтому в дальнейшем они подробно не рассматриваются и основное
внимание уделяется непрерывным процессам. Однако следует отметить, что для
дискретных процессов проходят почти параллельные выкладки. Переход процесса
размножения и гибели из состояния E
i
обратно в состояние E
i
представляет
непосредственный интерес только для дискретных цепей Маркова; в непрерывном
случае интенсивность, с которой процесс возвращается в текущее состояние, равна
бесконечности, и эта бесконечность была исключена согласно определению (13).
В случае процесса размножения и гибели с дискретным временем вероятности
переходов между состояниями
Здесь d
i
- вероятность того, что на следующем шаге (в терминах биологической
популяции) произойдет одна гибель, уменьшающая объем популяции до i-1 при
условии, что на данном шаге объем популяции равен i. Аналогично, b
i
- вероятность
рождения на следующем шаге, приводящего к увеличению объема популяции до i+1; 1-
d
i
-b
i
представляет собой вероятность того, что ни одно из этих событий не произойдет и
на следующем шаге объем популяции не изменится. Допускаются только эти три
возможности. Ясно, что d
0
=0, так как гибель не может наступить, если некому
погибать.
Однако в противовес интуиции допускается, что b
0
>0, что соответствует
возможности рождения, когда в популяции нет ни одного члена. Хотя это можно
расценивать как спонтанное рождение или божественное творение, но в теории
дискретных систем такая модель представляет собой вполне осмысленное допущение. А
именно, модель такова: популяция представляет собой поток требований, находящихся в
системе, гибель означает уход требования из системы, а рождение соответствует
поступлению в систему нового требования. Ясно, что в такой модели вполне возможно
поступление нового требования (рождение) в свободную систему. Матрица вероятностей
переходов для общего процесса размножения и гибели имеет следующий вид:
10
d
i
, j=i-1;
1-b
i
-d
i
, j=i;
b
i
, j=i+1;
0 в остальных случаях.
p
ij
=
