Лекции - Теория марковских случайных процессов
Подождите немного. Документ загружается.


Т=
010
000010
000001
0000001
2222
1111
00
iiii
bdbd
bdbd
bdbd
bb
Если цепь Маркова является конечной, то последняя строка матрицы записывается
в виде [0 0… 0d
n
1-d
n
]; это соответствует тому, что не допускаются никакие размножения
после того, как популяция достигает максимального объема n.
Матрица T содержит нулевые члены только на главной и двух ближайших к ней
диагоналях. Из-за такого частного вида матрицы T естественно ожидать, что анализ
процесса размножения и гибели не должен вызывать трудностей.
Далее будем рассматривать только непрерывные процессы размножения и гибели,
в которых переходы из состояния E
i
возможны только в соседние состояния E
i-1
(гибель) и
E
i+1
(рождение). Обозначим через
i
интенсивность размножения; она описывает скорость,
с которой происходит размножение в популяции объема i. Аналогично, через
i
обозначим интенсивность гибели, задающую скорость с которой происходит гибель в
популяции объема i. Заметим, что введенные интенсивности размножения и гибели не
зависят от времени, а зависят только от состояния E
i
, следовательно, получаем
непрерывную однородную цепь Маркова типа размножения и гибели. Эти специальные
обозначения введены потому, что они непосредственно приводят к обозначениям,
принятым в теории дискретных систем. В зависимости от ранее введенных обозначений
имеем:
i
= q
i,i+1
и
i
= q
i,i-1
.
Требование о допустимости переходов только в ближайшие соседние состояния
означает, что исходя из (14), q
ii
=-(
i
+
i
). Таким образом, матрица интенсивностей
переходов общего однородного процесса размножения и гибели принимает вид
Q =
3333
2222
1111
00
)(00
0)(0
00)(
000
Заметим, что за исключением главной и соседних с ней снизу и сверху диагоналей
все элементы матрицы равны нулю. Соответствующий граф интенсивностей переходов
представлен на рис. 4.
Более точное определение непрерывного процесса размножения и гибели состоит в
следующем: некоторый процесс представляет собой процесс размножения и гибели, если
он является однородной цепью Маркова с множеством состояний {E
0
, E
1
, E
2
, …}, если
рождение и гибель являются независимыми событиями (это вытекает непосредственно из
марковского свойства) и если выполняют следующие условия:
1) Pr [точно 1 рождение в промежутке времени (t,t+Δt)| объем популяции равен
i]=
)( tot
i
;
2) Pr [точно 1 гибель в промежутке времени (t,t+Δt)| объем популяции равен i]=
)( tot
i
;
3) Pr [точно 0 рождений в промежутке времени (t,t+Δt)| объем популяции равен
i]=
)(1 tot
i
;
11
.
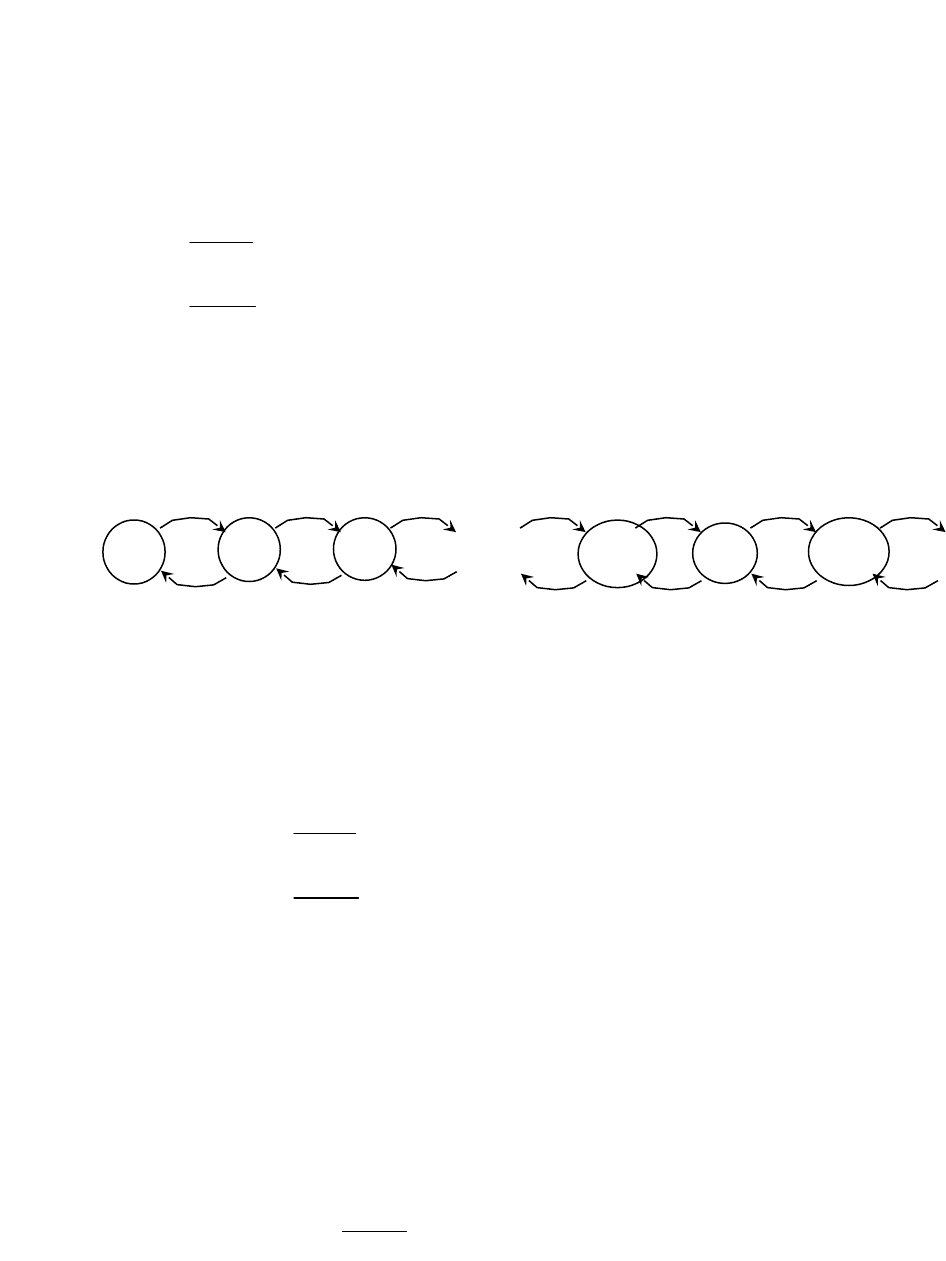
4) Pr [точно 0 гибелей в промежутке времени (t,t+Δt)| объем популяции равен i]=
)(1 tot
i
.
Согласно этим предположениям кратные рождения, кратные гибели и
одновременные рождения и гибели в течение малого промежутка времени (t, t+Δt)
запрещены в том смысле, что вероятность таких кратких событий имеет порядок о(Δt).
Вероятность того, что непрерывный процесс размножения и гибели в момент
времени t находится в состоянии E
i
(объем популяции равен i) определяется напрямую из
(16) в виде
.0),()(
)(
;1),()()()(
)(
1100
0
1111
itPtP
dt
tdP
itPtPtP
dt
tdP
iiiiiii
i
Для решения полученной системы дифференциальных уравнений в
нестационарном случае, когда вероятности P
i
(t), i=0,1,2,…, зависят от времени,
необходимо задать распределение начальных вероятностей P
i
(0), i=0,1,2,…, при t=0.
Кроме того, должно удовлетворяться нормировочное условие.
Рис.4. Граф интенсивностей переходов для процесса размножения и гибели.
Рассмотрим теперь простейший процесс чистого размножения, который
определяется как процесс, для которого
i
= 0 при всех i. Кроме того, для еще большего
упрощения задачи предположим, что
i
=
для всех i=0,1,2,... . Подставляя эти значения в
уравнения (18) получим
.0),(
)(
;1),()(
)(
0
0
1
itP
dt
tdP
itPtP
dt
tdP
ii
i
Для простоты предположим также, что процесс начинается в нулевой момент при нуле
членов, то есть:
.0,0
;0,1
)0(
i
i
P
i
Отсюда для P
0
(t) получаем решение
P
0
(t)=e
-
t
.
Подставляя это решение в уравнение (19) при i = 1, приходим к уравнению
t
etP
dt
tdP
)(
)(
1
1
.
Решение этого дифференциального уравнения, очевидно, имеет вид
P
1
(t)=
te
-
t
.
Далее по индукции в качестве решения уравнения (19) находим
12
(19)
(20)
(18)
0
1
i-1
i
1
2
i
i+1
E
0
E
2
E
1
E
i-
1
E
i
E
i+
1
…
…

0,0,
!
)(
)(
tie
i
t
tP
t
i
i
.
Это знакомое нам распределение Пуассона. Таким образом, процесс чистого размножения
с постоянной интенсивностью
приводит к последовательности рождений, образующей
пуассоновский процесс.
Наибольший интерес в практическом плане представляют вероятности состояний
процесса размножения и гибели в установившемся режиме. Предполагая, что процесс
обладает эргодическим свойством, т.е. существуют пределы
...,2,1,0),(lim
itP
i
t
перейдем к определению предельных вероятностей P
i
.
Уравнения для определения вероятностей стационарного режима можно
получить непосредственно из (18), учитывая, что dP
i
(t)/dt = 0 при
t
:
.0,0
;1,0)(
1100
1111
iPP
iPPP
iiiiiii
Полученная система уравнений решается с учетом нормировочного условия
0
1
i
i
P
Систему уравнений (21) для установившегося режима процесса размножения и
гибели можно составить непосредственно по графу интенсивностей переходов на рис.4,
применяя принцип равенства потоков вероятностей к отдельным состоянием процесса.
Например, если рассмотреть состояние E
i
в установившемся режиме, то:
интенсивность потока вероятностей в
1111
iiiii
PPE
и
интенсивность потока вероятностей из
1,)( iPE
iiii
.
В состоянии равновесия эти два потока должны быть равны, и поэтому непосредственно
получаем
iiiiiii
PPP )(
1111
Но это как раз и есть первое равенство в системе (21). Аналогично можно получить и
второе равенство системы. Те же самые рассуждения о сохранении потока, которые были
приведены ранее, могут быть применены к потоку вероятностей через любую замкнутую
границу. Например, вместо того, чтобы выделять каждое состояние и составлять для него
уравнение, можно выбрать последовательность контуров, первый из которых охватывает
состояние E
0
, второй - состояние E
0
и E
1
, и т.д., включая каждый раз в новую границу
очередное состояние. Тогда для i-го контура (окружающего состояния E
0
, E
1
, ..., E
i-1
)
условие сохранения потока вероятностей можно записать в следующем простом виде:
1,
11
iPP
iiii
.
Полученная система уравнений эквивалентна выведенной ранее. Для составления
последней системы уравнений нужно провести вертикальную линию, разделяющую
соседние состояния, и приравнять потоки через образовавшуюся границу.
Решение системы (23) можно найти методом математической индукции.
При i=1 имеем:
;
0
1
0
1
PP
при i=2:
;
0
21
10
1
2
1
2
PPP
при i=3:
13
(21)
(22)
(23)

.
0
321
210
2
3
2
3
PPP
и т.д.
Вид полученных равенств показывает, что общее решение системы уравнений (23)
имеет вид
,2,1,0,
0
21
110
iPP
i
i
i
или, учитывая, что, по определению, произведение по пустому множеству равно единице
1
0
1
0
,2,1,0,
i
k
k
k
i
iPP
Таким образом, все вероятности P
i
для установившегося режима выражаются через
единственную неизвестную константу P
0
. Равенство (22) дает дополнительное условие,
позволяющее определить P
0
. Тогда, суммируя по всем i, для P
0
получим:
1
1
0
1
0
1
1
i
i
k
k
k
P
Обратимся к вопросу о существовании стационарных вероятностей P
i
. Для того,
чтобы полученные выражения задавали вероятности, обычно накладывается требование,
чтобы P
0
> 0. Это, очевидно, налагает ограничение на коэффициенты размножения и
гибели в соответствующих уравнениях. По существу требуется, чтобы система иногда
опустошалась; это условие стабильности представляется весьма резонным, если
обратиться к примерам реальной жизни. Определим следующие две суммы:
1
1
0
2
1
1
0
1
1
.
;
i
i
k
k
k
i
i
k
k
k
S
S
Все состояния E
i
рассматриваемого процесса размножения и гибели будут
эргодическими тогда и только тогда, когда S
1
<
и S
2
=
. Только эргодический случай
приводит к установившимся вероятностям P
i
, i = 0, 1, 2, …, и именно этот случай
представляет интерес. Заметим, что условия эргодичности выполняются только тогда,
когда, начиная с некоторого i, все члены последовательности {
ii
/
} ограничены
единицей, т.е. тогда, когда существует некоторое i
0
(и некоторое С<1) такое, что для всех i
i
0
выполняется неравенство:
.1
1
C
i
i
14
