Лекции по ГИС
Подождите немного. Документ загружается.

151
установки солнечных батарей. Возможность определения распределений некоторых из этих
показателей может пригодиться, возможно, потому, что мы должны размещать дома,
растения или солнечные батареи одной большой группой (что характерно для кластерных
распределений), а не разрозненно. Мы можем также интересоваться выявлением
распределения объектов определенной области, таких как размытые поверхности, сорная
растительность или типы заселения для выяснения какой-нибудь возможной причины
образования наблюдаемых примеров.
Мы уже познакомились с понятием непосредственной окрестности на основе
смежности, определяемой как условие контакта полигональных объектов друг с другом
(Глава 9). Но, хотя простая мера смежности может быть полезна для рассмотрения размеров
соединенных полигонов одного типа, она мало что говорит нам о распределении,
образуемом этими региональными полигонами. Для этого применяется статистический
показатель (статистик) соединений (общих границ). Он не связан только лишь с
бинарными картами, но так как они лучше его иллюстрируют, и относительно просто
перейти от многокатегориальных карт к бинарным (что является обычной практикой), мы
ограничимся только случаем бинарных полигональных карт.
Соединение — это общая граница двух смежных полигонов. Статистик соединений
подсчитывает количество соединений в полигональном распределении и характеризует
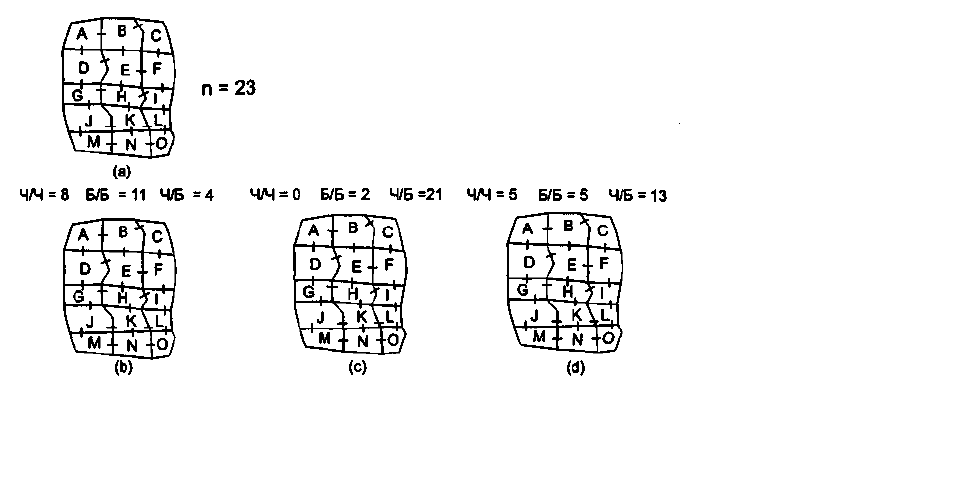
структуру соединений каждого покрытия. Посмотрите на Рисунок 19.2а, показывающий
область с пятнадцатью полигонами, и имеющимися между ними соединениями.
Рисунок 19.2. Статистик соединений для области
из 15 полигонов: а) 23 возможные соединения, b) кластерное
распределение, с) разреженное распределение, d) случайное распределение.
Всего между полигонами имеются 23 соединения (т.е. общих участков границ). На
Рисунке 19.2b среди них: 8 соединений между заштрихованными полигонами, 11 между
белыми и 4 между заштрихованными и белыми. Эти числа показывают, что между
заштрихованными и белыми полигонами имеется мало соединений, большинство белых
полигонов соединены друг с другом, и большинство заштрихованных полигонов соединены
друг с другом. Другими словами, полигоны сгруппированы, подобно тому, что мы прежде
наблюдали с точками. Рисунок 11.4с показывает совершенно другой набор чисел; здесь
большинство соединений (21 из 23) между полигонами разных классов, т.е. мы имеем
разреженное распределение. Рисунок 11.4d промежуточный случай: оба числа соединений
однородных полигонов низки, но не так, как на Рисунке 11.4с. Число разнородных
152
соединений также не настолько высоко, как в случае разреженного распределения. Таким
образом, здесь мы имеем дело со случайным распределением.
Теперь обратимся к вопросу об использовании результатов данного вида анализа.
Мы определили числа однородных и неоднородных соединений и можем выделить
три различных класса распределений. Но как в действительности сравнить результаты
анализа одной БД с тем, что можно было бы ожидать при кластерном, разреженном и
случайном распределениях? Главным образом, нас интересует случайность, она говорит о
том, что расположение полигонов скорее всего не зависит от какой-либо причины. И
наоборот в двух других случаях такая причина наверняка существует.
При анализе точечных распределений для оценки случайности мы обращались к
критерию χ
2
. Но этот показатель подразумевает, что мы знаем, каким должно быть
ожидаемое распределение в условиях случайности. Если бы мы знали подобные
распределения для полигонов (на основе числа соединений), то могли бы сравнивать их
точно таким- же способом.
Но как мы узнаем ожидаемое случайное распределение соединений, с которым могли
бы сравнить имеющиеся значения? Имеются два подхода к решению этой задачи. Первый,
называемый свободным отбором (free sampling), предполагает, что мы можем определить
ожидаемую частоту соединений внутри категорий и между ними либо на основе
теоретического знания моделируемой ситуации, либо исходя из известных распределений
для больших областей исследования. В первом случае, например, мы могли бы знать, что
вследствие определенных зональных установлений в городе, торговые центры или объекты
промышленности встречаются с определенной регулярностью по сравнению с другими
типами землепользования. И тогда мы могли бы сравнить эти распределения с
регулярностью торговых областей в другом городе, чтобы увидеть, используется такое же
зонирование или другое, приводящее к существенно другому распределению торговых
центров и объектов промышленности по сравнению с другими типами землепользования. Во
втором случае, т.е. при использовании известного распределения на большей изучаемой
области, могут быть выполнены подобные же сравнения. Скажем, нам известно
распределение полигональных соединений нашего округа из анализа сельхозкультур. Тогда
мы могли бы рассмотреть распределение их в отдельном пригородном районе и сравнить
число соединений в этой подобласти с числом соединений для всего округа, чтобы увидеть,
имеется ли сходство.
Второй подход, называемый несвободным отбором (nonfree sampling), применяется
более часто. Он не делает теоретических предположений о распределении и не полагается на
сравнение чисел соединений подобласти и всей области. В нем сравниваются числа
соединений оценочного случайного распределения с числом соединений наблюдаемого
распределения полигонов. Другими словами, мы создаем случайное
распределение, исходя только из самих полигонов. Тогда мы можем сравнить
имеющиеся результаты со случайным распределением, имея в виду отклонения от
случайности, говорящие о действии некоторого причинного механизма.
Другие меры распределений полигонов
Анализ распределений полигонов может быть весьма сложным, и связи ГИС с другим
программным обеспечением дают возможность выполнять его. Ландшафтные экологи часто
используют эти методы, обычно рассматривая полигоны как островки (patches), особенно по
отношению к большему, более однородному окружению (background), так называемой
матрице (matrix). Вы найдете меры полигональной изолированности (polygonal isolation),
меры доступности (accessibility), взаимодействий полигонов (polygon interactions) и
рассредоточенности (dispersion). Поскольку многие из этих мер заимствованы из
литературы по географии, биогеографии, экологии, лесоводства и других дисциплин,
153
примеры будут достаточно разнообразны, чтобы дать вам представление о возможностях
использования этих дополнительных мер.
РАСПРЕДЕЛЕНИЯ ЛИНИЙ
Мы встречаем линейные паттерны постоянно, нечасто и пропускаем их. Улицы и
шоссе образуют узнаваемый паттерн, который мы относим к сетям, создаваемым человеком
для перемещения людей и вещей между пространственно распределенными точками,
называемыми городами. Нам встречаются ограждения, также имеющие определенные
конфигурации и количества в зависимости от размеров полей, участков, форм полигонов,
которые они окружают. Полосы на открытых участках коренной породы показывают
параллельные линии перемещения камней под ледником, проходившем тысячи лет назад.
Механизмы, вызвавшие образование каждого из этих линейных паттернов, лучше всего
могут быть поняты, если мы прежде определим конкретные параметры соответствующих
распределений.
Плотность линий
Поскольку линии в отличие от точек имеют пространственную протяженность, анализ
их распределений несколько сложнее. Одни исследователи изучали распределения длин
линий, другие рассматривали интервалы между линиями, во многом подобно анализу
ближайшего соседа в точечных распределениях.
Мы рассмотрим эти и другие меры распределений линий в последующих параграфах,
и начнем с простейшей меры плотности линий.
Мы определили плотность безразмерных точек как отношения их числа к занимаемой
ими площади. Плотность двухмерных полигонов определялась как отношение суммарной
площади класса к площади всей карты. Подобным же образом, для определения плотности
одномерных линий мы будем использовать отношение суммы их длин к площади покрытия.
Выражаться оно может в метрах на гектар или километрах на квадратный километр. За
исключением сравнения с аналогичными величинами для других регионов или для того же
региона в другие моменты времени, мы мало что можем сделать с этой информацией.
Поэтому сейчас мы рассмотрим другие показатели распределений линий, аналогично тому,
как было с распределениями точек и полигонов.
Ближайшие соседи и пересечения линий
Распределение пар линий может быть определено во многом подобно тому, как мы
поступали с точками, хотя вычисления несколько усложняются, так как, в отличие от точек,
линии имеют размерность. Может показаться, что следует просто выбрать центр каждой
линии и провести анализ ближайшего соседа для этих точек. Однако, вследствие того, что
линии имеют различные длины, эта процедура не даст нам правдивой картины
распределения самих линий. С точки зрения статистики часто считается полезным делать
случайную выборку. Следуя этому подходу, нашей первой задачей в анализе ближайших
соседей среди линейных объектов будет выбор случайной точки на каждой линии карты (или
на каждом сегменте линии, если они не прямые). Далее, опускается перпендикуляр из

154
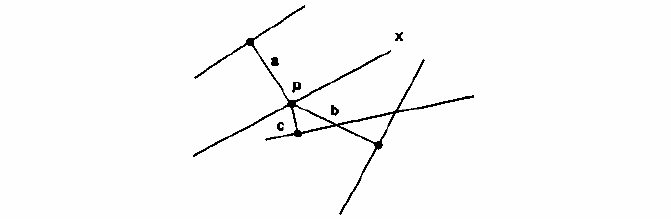
этой точки к ближайшей линии (Рисунок 11.5). Затем мы измеряем, эти расстояния и
подсчитываем среднее РБС. Как со всеми РБС, мы должны иметь возможность оценить эту
величину по отношению к случайному распределению. Дэйси [Dacey, 1967] определил
значения для ожидаемых РБС, дисперсии и стандартной ошибки случайного распределения
линий. Эти величины позволяют нам сравнить ожидаемое и наблюдаемое и создать
статистический показатель, по которому можно протестировать гипотезу о случайности
[Davis, 1986]. По указанной ссылке можно найти описание соответствующих формул.
Этот критерий работает для большинства распределений линий, будь линии
прямыми или изогнутыми, но имеет и некоторые ограничения. Если линии очень извилисты,
этот подход — менее чем успешен.
Рисунок 11.5. Расстояние до ближайшего соседа среди линий.
Поиск ближайшего соседа между линиями с
использованием случайно выбранной точки на одной из них.
Кроме того, чтобы критерий был полезен, линии должны быть по меньшей мере в
полтора раза длиннее среднего расстояния между ними. Если количество линий в покрытии
мало, оценка плотности, используемая в анализе ближайшего соседа должна быть
скорректирована весовым коэффициентом (n-1)/n, где n число линий распределения. То
есть, вместо отношения суммы длин на площадь мы используем формулу
(n-l)L/nA,
где L сумма длин, а А площадь. Эта скорректированная плотность линий
улучшит качество статистика ближайшего соседа.
Методы пересечения линий являются альтернативой при анализе распределения
линий. Один простой подход состоит в том, чтобы преобразовать двухмерный паттерн в
одномерную последовательность прочерчиванием выборочной линии через карту и учетом
пересечений этой линии с линиями покрытия. Существуют по меньшей мере два способа
создания таких линий. Первый случайно выбрать пару точек и соединить их линией.
Второй метод состоит в проведении луча из случайной точки под случайным углом,
откладывании случайного расстояния от начальной точки и проведении перпендикуляра к
лучу из этой точки. После того, как линия проведена, может быть рассмотрено
распределение интервалов между пересечениями ее с линиями покрытия с использованием
стандартных методов анализа наборов данных. Альтернативой одиночной линии является
зигзагообразная, которая пересекает покрытие два или три раза. Зигзагообразный путь (часто
называемый случайным обходом (random walk)) также создаст серию пересечений,
расстояния между которыми опять же могут быть проанализированы любым статистическим
методом для последовательностей данных (Рисунок 11.6).
Рисунок 11.6. Метод случайного обхода для оценки распределения линий.
Модификация метода пересечений с использованием зигзагообразной линии для получения точек выборки.

155
НАПРАВЛЕННОСТЬ ЛИНЕЙНЫХ И ПЛОЩАДНЫХ ОБЪЕКТОВ
Линейные объекты могут характеризоваться не только распределением по ландшафту,
но и ориентацией. Такие объекты как осадочные напластования, русла ледников,
переносимая водой галька, цепи валунов, оставленные ледниками, ограждения, сети улиц,
ветровал деревьев в лесу имеют определенную ориентацию, которая часто указывает на
породившую их силу.
Но когда мы анализируем ориентацию, у нас может возникнуть ситуация выбора
между двумя встречными направлениями. Если линейный объект является улицей с
односторонним движением, то ориентация ее самой не говорит нам о направлении, в
котором должен двигаться транспорт. Поэтому, кроме ориентации нам нужно знать и о
направленности (directionality). Мы можем также рассматривать распределения линейных
объектов либо как двухмерные, либо как трехмерные, с учетом углового направления
относительно поверхности сферы. Для простоты мы ограничимся лишь первыми.
В традиционном статистическом анализе ориентации линий с карты переносятся на
диаграмму направлений (rose diagram), где все они прочерчиваются из одной начальной
точки. На некоторых диаграммах направлений длиной линий также изображают параметры
объектов, такие как сила ветра или длина изгороди. Диаграммы направлений полезны для
визуальной оценки, но измерения, получаемые непосредственно по данным покрытия
больше подходят для численного анализа. Первым мы рассмотрим равнодействующий
вектор (vector resultant). В качестве примера можно вспомнить басню про лебедя, рака и
щуку. Зная силы и направления, приложенные к возу, можно определить, в какую сторону и
с каким ускорением объект начнет движение.
Для демонстрации двухмерного анализа направлений возьмём большое количество
деревьев, поваленных прямолинейным ветром. Каждое дерево может быть отображено как
линейный объект покрытия, при этом записываются координаты вершины и основания
каждого дерева, давая нам ориентацию каждого дерева (Рисунок 11.7).
Рисунок 11.7. Распределение направлений поваленных деревьев.
Карта показывает общую тенденцию и
некоторые отклонения от нее.
Метеорологи хотят выяснить общее направление ветра по поваленным деревьям, но
эти деревья не имеют единой для всех ориентации, поэтому нашей первой задачей является
определение равнодействующего вектора поваленных деревьев.
С каждым деревом ассоциируется вектор с началом в основании дерева и углом Q в
сторону вершины. Мы умножаем длину каждого дерева на косинус этого угла для получения
Х-составляющей, а также на синус этого угла для получения Y-составляющей. Для
вычисления равнодействующего вектора мы складываем эти величины для каждой

156
составляющей, и полученные значения равнодействующего вектора Х
r
и Y
r
показывают
преобладающее направление вершинных точек деревьев в ветровале. Рисунок 11.8
показывает равнодействующий вектор R, полученный из трех векторов А, В и С.
Мы можем определить среднее направление Q исходя из
равнодействующего вектора по формуле: Q = arctan (Y
r
/ X
r
).
Рисунок 11.8. Равнодействующий вектор.
Так как среднее направление наших векторовr зависит не только от разброса деревьев,
но и от числа наблюдений, мы можем нормализовать эти величины делением координат
каждого равнодействующего вектора на число линейных объектов покрытия. Это позволит
нам сравнивать две различные области, например, две области ветровала на предмет общего
направления ветра*.
Как и с любым набором точек, где средняя величина служит мерой центральной
тенденции данных или тенденции данных группироваться вокруг некоторой центральной
точки, мы можем использовать среднее для получения других статистических показателей,
которые определяют разброс от среднего. Рисунок 11.9 показывает два случая
равнодействующего вектора R с тремя исходными. Когда векторы расположены близко к
одному направлению, равнодействующий вектор будет длинным, в то время как при широко
разбросанных исходных векторах значительно более коротким. В нашем примере из
басни это выглядит как сложение усилий участников в общем направлении или же скорее
противодействие друг другу, приводящее к существенно меньшей равнодействующей силе,
прилагаемой к возу.
* Следует отметить, что здесь угол отсчитывается от оси Y, а не от оси X, как принято в математике. В формуле вычисления
составляющих длина дерева является весовым коэффициентом для его направления. Чтобы каждое дерево вносило одинаковый вклад,
следует приравнять его длину единице. Тогда среднее направление будет равно арктангенсу отношения суммы косинусов к сумме синусов
направлений деревьев. Для данного примера можно также /отметить, что более длинные деревья скорее всего будут лучше представлять
среднее направление, так что нормализация будет излишней. — прим, перев.

157
Рисунок 11.9. Разброс векторов
. Равнодействующие векторы для случаев близких и разбросанных исходных
линий.
Длина равнодействующего вектора (resultant length) может быть определена по
формуле:
Таким образом, мы имеем не только среднее направление лесовала, но и меру
компактности распределения: чем компактнее распределение, тем длиннее эта линия.
Для сравнения длины равнодействующего вектора в данном месте с другим местом,
нам следует, опять же, нормализовать данные. Нормализованная длина равнодействующего
вектора получается делением длины равнодействующего вектора R на сумму длин
образующих его векторов.
Это безразмерная величина в диапазоне от 0 до 1, напоминающая дисперсию в
традиционной статистике, так как является мерой пространственного разброса вокруг
среднего значения. Правда, она выражает этот разброс "наоборот": большие значения
соответствуют более близкой ориентации векторов, меньшие - большему разбросу. Таким
образом, большое значение этого показателя в нашем примере с деревьями означало бы
значительное преобладание одного из направлений ветра, а малое значение говорило бы о
наличии завихрений или отсутствии явно преобладающего направления. Наряду с самой
этой величиной можно использовать также и обратную ей величину, называемую круговой
дисперсией (circular variance), которая равна единице минус нормализованная длина
равнодействующего вектора. Если вы интересуетесь статистикой, то можете увидеть
возможность существования дирекционных аналогов стандартного отклонения, моды и
медианы, для которых также имеются соответствующие формулы [Gaile and Burt, 1980].
Остается одна проблема, связанная с ориентацией и направлением. Как мы знаем,
одни линейные объекты могут иметь определенное направление (деревья), другие же нет
(лесозащитные полосы), хотя определенная ориентация присутствует в обоих случаях.
Например, один исследователь, собирающий данные о заграждениях, может указывать, что
некоторые из них ориентированы на север, а другой что на юг. Тогда, при анализе
данных, собранных этими исследователями, может оказаться, что при определении длины
среднего равнодействующего вектора, исходные векторы будут, так сказать, взаимно
уничтожать друг друга.
К счастью, для этого есть остроумное решение. Крумбейн [Krumbein, 1939]
обнаружил, что при удвоении значения угла, независимо от исходного направления,
записывается одно и то же значение. Допустим, мы имеем объект, ориентированный с
северо-запада (315°) на юго-восток (135°). После удвоения мы получим: 315° × 2 = 630° (-
360° = 270°) и 135° × 2 = 270°. Такой способ выражения направлений повлияет на формулы
для вычисления среднего направления, нормализованной длины равнодействующего вектора
и круговой дисперсии, поэтому, чтобы получить действительные значения, их нужно будет
модифицировать.
Эти простые меры направленности и разброса могут быть проверены на случайность
[Batschelet, 1965; Gumbel et al., 1953] и наличие тренда [Stephens, 1969] стандартными
процедурами проверки статистических гипотез. С дирекционными данными покрытия могут
сравниваться аналогичные данные других покрытий [Gaile and Burt, 1980; Mardia, 1972]. Эти
темы выходят за рамки данной книги, а указанные источники предлагают подробное их
рассмотрение.
В контексте ГИС, данные меры главным образом помогают охарактеризовывать
распределения внутри покрытия и сравнения их с данными других покрытий в поисках
причинных механизмов. Растровые ГИС плохо приспособлены для данного типа анализа, но
большинство векторно-топологических систем позволяют определить по меньшей мере
(
)
2
r
2
r
YXR +=
158
некоторые предварительные значения (например, углы отрезков полилиний), которые могут
храниться в БД ГИС как атрибуты и передаваться другим программам для обработки, если
сам ГИС-пакет не способен вычислять средние показатели направленности.
СВЯЗНОСТЬ ЛИНЕЙНЫХ ОБЪЕКТОВ
Важным аспектом пространственного расположения линий является их способность
образовывать сети. Сети имеют самые разнообразные формы, как естественные, так и
созданные человеком. Среди них: автомобильные и железные дороги, телефонные линии,
реки, даже лесозащитные полосы могут играть роль сети, позволяющей мелким
млекопитающим перемещаться по ландшафту, список можно долго продолжать. И хотя
мы можем интересоваться плотностью и ориентацией объектов, образующих сеть, нам
нужна также и возможность анализировать реальные связи, образованные этими объектами и
степень связанности между различными точками сети. Вы наверняка сталкивались с
ситуациями, когда в городе нет прямой дороги от места до места, и приходится ехать
кружным путем. Здесь мы сталкиваемся с недостатком связности (connectivity) в сети.
Связность является мерой сложности сети. Имеются несколько методов для
определения этой характеристики [Haggett et al., 1977; Lowe and Moryadas, 1975; Sugihara,
1983; Taafle and Gauthier, 1973]. Наиболее общими являются гамма-индекс (gamma index) и
альфа-индекс (alpha index).
Гамма-индекс γ является отношением числа существующих связей между парами
узлов сети, L, к максимально возможному числу связей в том же наборе узлов, L
max
.
Очевидно, что векторно-топологическая модель данных лучше всего подходит для этих
вычислений. Определить же L
max
не так трудно, как может поначалу показаться, оно
однозначно определяется числом узлов V. Например, если мы имеем три узла, то возможны
лишь три связи (Рисунок 11.10). Если мы добавим еще один узел, то сможем добавить еще
три связи, а всего их будет шесть [Forman and Godron, 1987]. И если мы полагаем, что не
образуются новые пересечения, то максимальное число связей будет каждый раз
увеличиваться на три. То есть, L
max
= 3(V - 2).
Гамма-индекс тогда определяется как
γ = L / L
max
= L / 3(V-2)
Он принимает значения от 0 (нет ни одной связи) до 1 (все возможные связи
присутствуют) [Forman and Godron, 1987].
Рисунок 11.10 показывает два варианта сети с 16-ю узлами. На рисунке
(a) имеется 15 связей, что дает связность γ = 15 / 3(16-2) = 0.36. На рисунке
(b) имеется 20 связей, поэтому γ = 20 / 3(16-2) = 0.48. Образно говоря, первая сеть
связна примерно на треть, а вторая — наполовину.
Большее количество связей в сети облегчает передвижение по ней, что важно,
например, для специалистов по транспортному планированию.
Важной характеристикой сетей помимо связности является наличие в ней контуров,
позволяющих перемещаться от узла к узлу разными маршрутами. В качестве примера можно
привести кольцевые автодороги вокруг крупных городов, позволяющие снизить нагрузку
транзитного транспорта на уличную сеть.
159
Рисунок 11.10. Гамма-индекс.
Две различные сети на основе одного набора узлов: а) с минимальной связностью и
без контуров, b) с большей связностью и контурами, дающими альтернативные маршруты перемещения по сети.
В качестве меры соединенности узлов контурами альтернативных маршрутов
(circuitry) используется так называемый альфа-индекс (а). Он является отношением
имеющегося в сети числа контуров к максимально возможному числу контуров в этой сети.
Известно, что сеть без контуров имеет связей на одну меньше, чем число узлов: L = V - 1. На
Рисунке 11.10а вы можете видеть такую сеть, в ней 16 узлов и 15 связей. Она обладает
минимальной связностью, в том смысле, что в ней имеется наименьшее возможное число
связей при заданном числе узлов, причем каждый узел имеет по меньшей мере одну связь.
Добавление какой-либо связи создает контур, т.е. когда сеть содержит контуры L > V
- 1. Число же имеющихся контуров можно определить как L -(V- 1) [Forman and Godron,
1987].
Далее, так как максимальное число связей в сети определяется как 3(V -2), а
минимальное (без потери связности) как V - 1, то максимальное число контуров будет 3(V -
2) - (V - 1), т.е. 2V - 5. Отсюда альфа-индекс α = (L - (V - 1)) / (2V - 5). Диапазон значений
альфа-индекса - от 0 (сеть без контуров) до 1 (сеть с максимальным числом контуров).
Теперь мы можем вычислить альфа-индекс для сетей на Рисунке 11.10:
α = (15-16+ 1)/(2×16-5) = О
α = (20-16 + 1)/(2×16-5) = 0.19
Таким образом, в сети на Рисунке 11.10а есть только один вариант для перемещения
из одной точки в другую, а на Рисунке 11.10b возможны несколько альтернативных
маршрутов разной длины.
Поскольку для создания контуров требуется добавление новых связей, вполне
возможно рассматривать альфа-индекс как альтернативную меру связности. Но так как эти
два индекса дают разные взгляды на сеть, будет более уместным объединить их некоторым
образом для создания общей меры сложности сети (network complexity). Для вычисления
данных индексов требуется использование векторной ГИС. Это требование подчеркивается
тем обстоятельством, что вся эта статистика имеет топологическую основу теории графов,
где гораздо важнее связность узлов, нежели их расположение или длины и формы линий,
связывающих их.
Для транспортного моделирования нам нужно знать все-таки больше, чем просто
параметры связности. Здесь имеют значение длины связей между узлами, возможные
направления движения по этим линиям, значения сопротивления движению (импеданса).
Вдобавок, существуют и другие простые индексы, пришедшие из теорий транспортировки и
связи, которые также характеризуют связность сетей. Например, возможно определение
интенсивности связности (linkage intensity) для каждого узла, числа альтернативных
маршрутов между заданными узлами, поиск центрального узла (central place), т.е. такого,
который имеет наибольшее число связей, а также построение регионов на основе связности и
160
доступности [Haggett et al., 1977; Lowe and Moryadas, 1975]. И все это можно сочетать друг с
другом и с другими характеристиками линий расположением, ориентацией, дисперсией
— для получения более полной картины сети.
МОДЕЛЬ ГРАВИТАЦИИ
До сих пор мы не обращали внимание на значимость отдельных узлов, которая может
быть неодинаковой. Но подумайте о городах. Крупные города по сравнению с мелкими дают
больше возможностей для покупок, для посещения выставок, концертов, спортивных
соревнований и т.д. Поэтому они привлекают больше людей. И города - не единственный
пример, когда размер имеет значение. Например, большое озеро привлекает больше
водоплавающих птиц, нежели маленький пруд.
Оба примера показывают, что более крупные объекты привлекают к себе большую
активность, будь то птичью, или человечью. Размер такого притяжения может
представляться во многом подобно гравитационному притяжению тел, обладающих массой.
Чем больше масса, тем больше сила притяжения между ним и его соседями.
Перенося идею гравитационного притяжения на взаимодействие между узлами
покрытия ГИС, мы получим модель гравитации (gravity model), которая в общем виде
выражается как:
где L.
ij
- величина взаимодействия между узлами i и j; P
i
- величина узла i; P
j
-
величина узла j; d - расстояние между узлами; К - константа, определяемая природой
взаимодействующих объектов. Величины узлов могут быть представлены такими их
параметрами, как потребность в продукции, объем розничных продаж торговых центров
города, площадью поверхности водоема для водных птиц.
Мы видим, что чем больше величины узлов, тем больше сила взаимодействия между
ними, и что с ростом расстояния между узлами сила взаимодействия уменьшается. На
примере города мы можем сказать, что чем больше город, тем более он привлекателен для
торговли. С другой стороны, если город находится далеко от вас, вряд ли вы в него поедете,
даже несмотря на возможную выгоду от сделки. [Как говорит русская поговорка, "за рекой
телушка — полушка, да рубль перевоз".]
Существуют многие варианты данной простой модели притяжения между точками,
как в растровых, так и в векторных системах. И хотя большинство из них используется для
экономического анализа размещения объектов (также как и полигоны Тиссена), возможно и
другое их применение. Исследователи могут использовать их для описания пассажиропотока
между городами, объема телефонных вызовов, потоков птиц и семян, которые
распространяются птицами между участками леса [Buell et al., 1971; Carkin et al,, 1978;
McDonnell, 1984; McQuilkin, 1940; Whitcomb, 1977]. В общем, любые потоки между узлами
различной величины могут анализироваться с применением модели гравитации.
МАРШРУТИЗАЦИЯ И АЛЛОКАЦИЯ
Среди наиболее применяемых приложений сетей в ГИС являются родственные задачи
маршрутизации и размещения (аллокации) (routing and allocation). Простейший вариант
маршрутизации включает поиск кратчайшего маршрута между двумя узлами сети (Рисунок
11.11). Учитывая, что узлам могут присваиваться весовые коэффициенты (как в модели
гравитации), возможен вариант маршрутизации от некоторой заданной точки до ближайшей
точки с максимальным весом (например, максимальным спросом на товар). Прекрасное
описание маршрутизации и размещения можно найти в [Lupien et al., 1987].
Каждой связи в сети может быть присвоено значение импеданса (сопротивления,
стоимости), во многом наподобие фрикционной поверхности, но налагаемого только на саму
2
jiij
dPKPL =
