Лекции по ГИС
Подождите немного. Документ загружается.

131
До сих пор мы имели дело с линейной интерполяцией, предполагая, что поверхность
изменяется линейным образом. Однако, последовательность отсчетов высоты не всегда
следует линейному закону. В некоторых случаях она скорее логарифмическая, в других
может предсказываться только для небольших участков поверхности. В таких случаях
линейная интерполяция не даст адекватных результатов. Кроме того, существуют и другие
подходы к поверхностной информации, которые могут потребовать определения общего
закона изменения поверхности, а не детального ее описания. Некоторые из этих методов
могут быть весьма сложными математически, так что мы ограничимся концептуальным
уровнем рассмотрения некоторых методов нелинейной интерполяции, чтобы понять, как их
можно использовать в ГИС наилучшим образом.
Другие методы интерполяции
Здесь мы рассмотрим три метода интерполяции: метод обратных взвешенных
расстояний (ОВР), метод поверхности тренда и кригинг.
Метод ОВР исходит из предположения, что чем ближе друг к другу находятся точки
данных, тем ближе их значения. Например, двигаясь по склону холма, вы можете отметить
большее сходство в значениях высоты в близлежащих к вашему текущему положению
точках по сравнению с точками, которые удалены гораздо дальше. То же можно было бы
сказать, если бы вы двигались по равнине. Для более точного описания топографии нам
нужно выбрать точки окрестности, которые демонстрируют это сходство поверхности. Это
достигается несколькими приемами поиска, включая определение окрестности на заданном
удалении от каждой точки, предварительным заданием числа точек выборки данных или
выбором определенного числа точек в квадрантах.
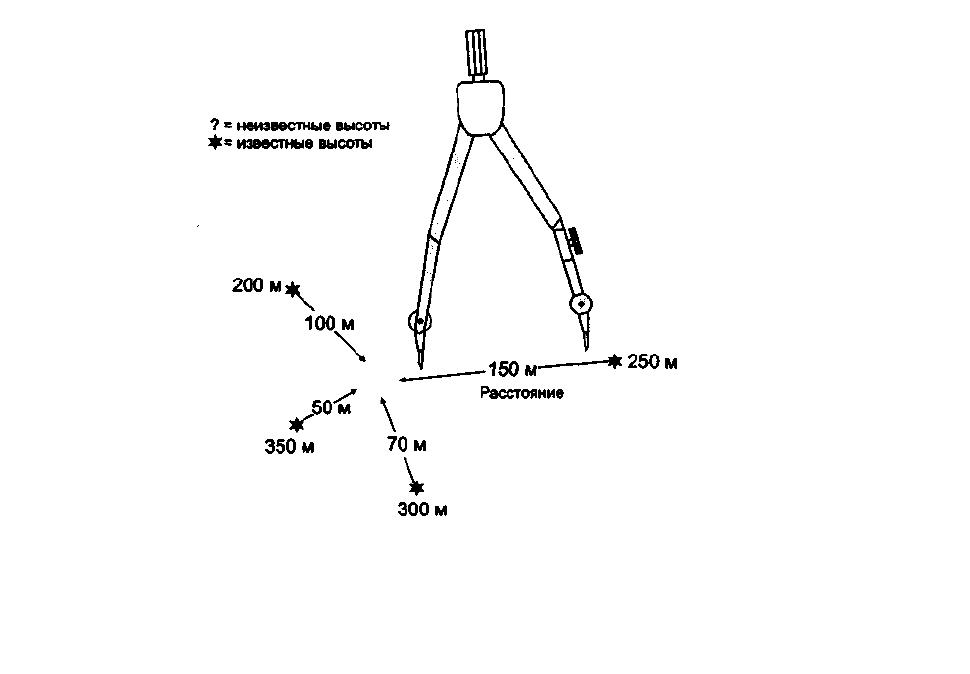
Рисунок 17. . Интерполяция со взвешиванием по расстоянию.
Заметьте, что близкие точки оказывают большее
влияние, чем удаленные. Например, недостающая величина будет ближе к отметке высоты 350 вследствие ее большей
близости к интерполируемой точке.
132
Какой бы метод ни использовался, компьютер должен измерять расстояние между
каждой парой точек и от каждой начальной точки. Затем значение высоты в каждой точке
взвешивается в зависимости от квадрата расстояния, так что более близкие точки вносят
больший вклад в определение интерполируемой высоты по сравнению с более удаленными
(Рисунок 17. ). Существуют многие модификации этого подхода. Одни методы сокращают
объем вычислений применением "поиска с обучением", другие используют в качестве
весового коэффициента вместо второй степени третью или более высокую, третьи
учитывают барьеры, представляющие береговую линию, скалы или иные непреодолимые
объекты, которые могут воздействовать на результаты интерполяции. Как и при
использовании барьеров в других задачах моделирования, процесс интерполяции не может
распространяться через барьер.
В некоторых случаях нас больше интересует общие тенденции поверхности, нежели
точное моделирование мелких неровностей. Например, нас может интересовать общее
распределение населения по стране для демографического исследования, или подход к
каменноугольному пласту с поверхности, чтобы определить, сколько необходимо удалить
поверхностного грунта. Наиболее распространенный подход к такой характеристике
поверхности называется поверхностью тренда.
Как и в методе ОВР, для поверхностей тренда мы используем наборы точек в
пределах заданной окрестности, которая строится на основе любого из способов,
перечисленным для методов со взвешиванием. В пределах каждой окрестности строится
поверхность наилучшего приближения на основе математических уравнений, таких как
полиномы или сплайны (polynomials, splines). Эти уравнения являются нелинейными
зависимостями, которые аппроксимируют кривые или другие формы числовых
последовательностей. Чтобы построить поверхность тренда, каждое из значений в
окрестности подставляется в уравнение. Из уравнения, использованного для построения
поверхности наилучшего приближения, получается одно значение и присваивается
интерполируемой точке. Процесс продолжается для других целевых точек; кроме того,
поверхность тренда может быть расширена на все покрытие.
Число, присваиваемое целевой ячейке, может быть простым средним всех значений
поверхности в окрестности, или оно может быть взвешенным с учетом определенного
направления, в котором ориентирован тренд. Поверхности тренда, могут быть плоскими,
показывая общую тенденцию для всего покрытия, или они могут быть более сложными. Тип
используемого уравнения (или степень полинома) определяет величину волнистости
поверхности. Чем проще выглядит поверхность тренда, тем меньший порядок, как говорят,
она имеет. Например, поверхность тренда первого порядка будет выглядеть как плоскость,
простирающаяся под некоторым углом по всему покрытию, т.е. она имеет тенденцию в
одном направлении. Если поверхность имеет один изгиб, то такую поверхность называют
поверхностью тренда второго порядка (Рисунок 17. ), и т.д.
Последний рассматриваемый метод интерполяции, кригинг (kriging), оптимизирует
процедуру интерполяции на основе статистической природы поверхности. Кригинг
использует идею регионализированной переменной (regionalized variable), которая
изменяется от места к месту с некоторой видимой непрерывностью, но не может
моделироваться только одним математическим уравнением. Оказывается, многие
топографические поверхности подходят под это описание, также как и поверхности
изменения качества руды, вариации качества почв и даже некоторые показатели
растительности.
133
Рисунок 17 7. Порядки поверхностей тренда.
Поверхности первого, второго и третьего порядка в зависимости от
сложности полинома, используемого для представления поверхности.
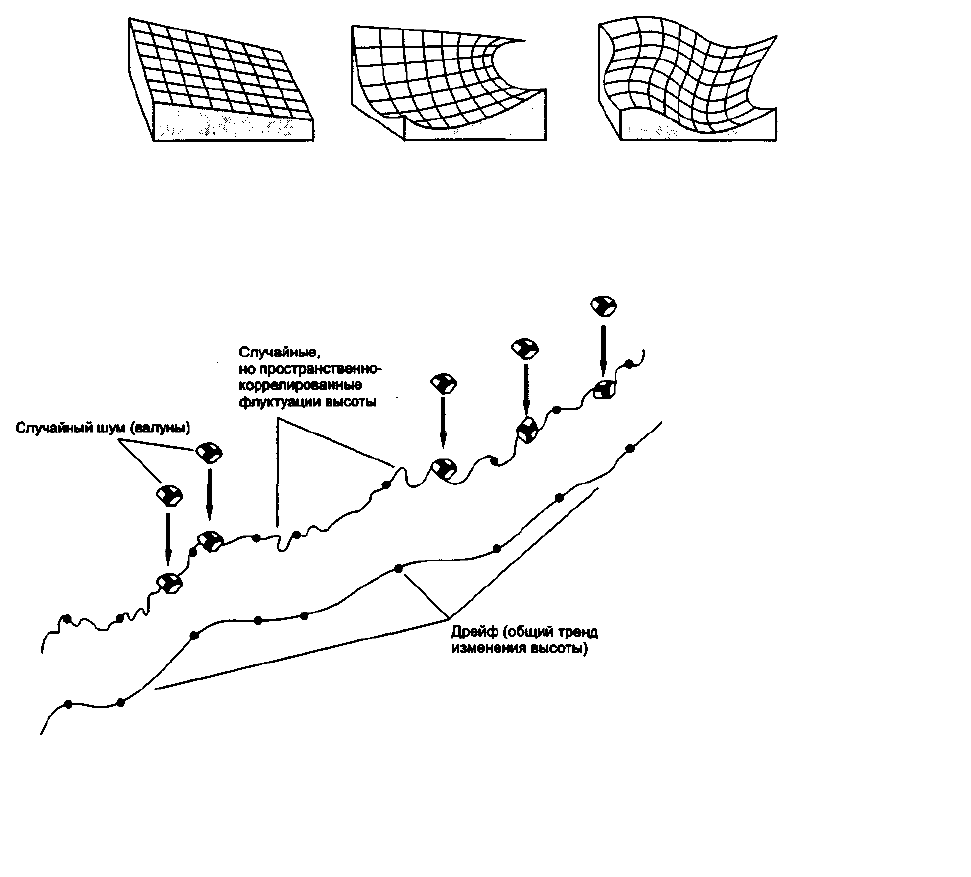
Рисунок 17. . Элементы кригинга.
Дрейф (общая тенденция), случайные, но пространственно коррелированные
высотные колебания (небольшие отклонения от общей тенденции), и случайный шум (камни), иллюстрируемые восхождением
по склону горы.
Кригинг обрабатывает эти поверхности так, считая их образованными из трех
независимых величин. Первая, называемая дрейфом или структурой (drift or structure)
поверхности, представляет поверхность как общий тренд в определенном направлении.
Далее, кригинг предполагает, что имеются небольшие отклонения от этой общей тенденции,
вроде маленьких пиков и впадин, которые являются случайными, но все же связанными друг
с другом пространственно (мы говорим, что они пространственно коррелированны).
Наконец, мы имеем случайный шум (random noise), который не связан с общей тенденцией
и не имеет пространственной автокорреляции. С каждой из трех переменных надо
оперировать в отдельности. Дрейф оценивается с использованием математического
уравнения, которое наиболее близко представляет общее изменение поверхности, во многом
подобно поверхности тренда. Ожидаемое значение высоты измеряется с использованием
вариограммы (variogram, semivariogram) (Рисунок 17. ), на которой по горизонтальной оси
откладывается расстояние между отсчетами, называемое лагом (lag), вертикальная ось несет
так называемую полудисперсию (semivariance), которая определяется как половина
дисперсии (квадрата стандартного отклонения) между каждым значением высоты и его
соседями.
Таким образом, полудисперсия является мерой взаимосвязи значений высоты,
зависящей от того, как близко друг к другу они находятся. Затем через точки данных
проводится кривая наилучшего приближения, давая нам меру пространственно-
коррелированной случайной компоненты. Посмотрев внимательно на график полудисперсии,
134
вы можете заметить, что когда расстояние между точками отсчета высоты мало,
полудисперсия тоже мала. Это значит, что значения высоты близки и, следовательно,
взаимосвязаны вследствие их пространственной близости. С ростом расстояния между
точками растет и полудисперсия, показывая быстрый спад пространственной корреляции
значений. Наконец достигается критическое значение лага, известное как предельный
радиус корреляции (range), при котором дисперсия достигает предела и в дальнейшем
остается постоянной. Чем ближе друг к другу находятся отсчеты внутри диапазона роста (т.е.
от нуля до точки прекращения роста кривой на графике), тем более похожими они должны
быть. За пределами радиуса корреляции расстояние между точками не имеет значения, они
совершенно независимы на любом удалении, превышающем радиус. Это говорит нам о том,
какая окрестность должна быть использована (например, в ОВР-интерполяции), чтобы
охватить все точки, значения, высоты которых будут взаимосвязаны.
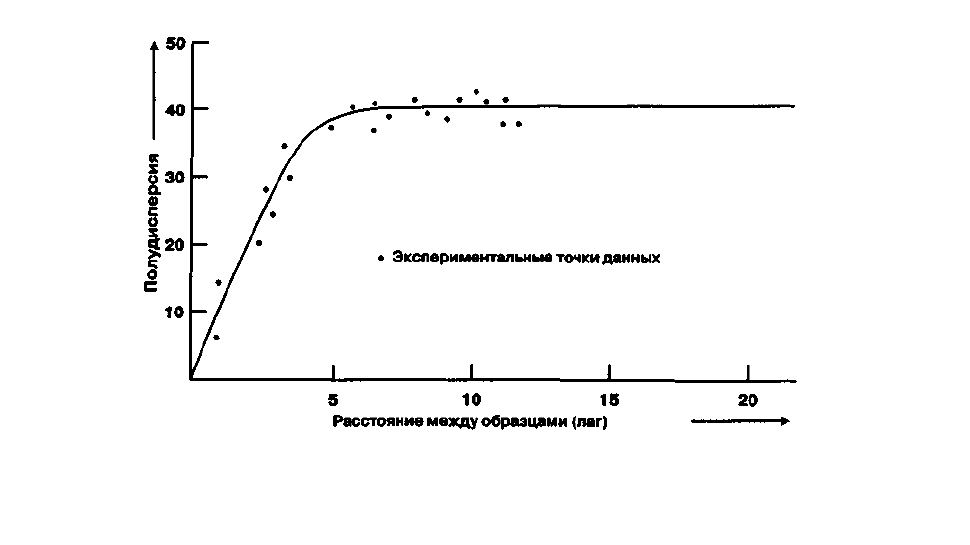
Рисунок 17. . Пример вариограммы.
Она показывает связь между точками данных и аппроксимирующей линией.
Обратите внимание, что в некотором диапазоне значений лага высоты связаны друг с другом (дисперсия высот связана с
лагом), а вне его нет вообще никакой связи (дисперсия достигает максимального значения), так как точки находятся слишком
далеко друг от друга.
Третьим по важности моментом графика является то, что аппроксимирующая кривая
не проходит через начало координат. По идее, если между отсчетами нет расстояния, то не
должно быть и дисперсии, так как отсчеты являются по сути одной точкой. Но нужно
помнить, что кривая является оценочной. Разница между нулевой дисперсией при нулевом
лаге и предсказываемым положительным значением является остаточной, пространственно
некоррелированной "шумовой" дисперсией, которая называется остаточной дисперсией
(nugget variance). Эта остаточная дисперсия объединяет дисперсию ошибок измерения с
пространственной дисперсией, которая имеет место на расстояниях, гораздо меньших, чем
интервал взятия отсчетов, и которые в дальнейшем не могут быть устранены.
Теперь, имея три составляющие регионализированной переменной, определенные
вариограммой, мы можем определить веса, необходимые для выполнения интерполяции в
локальных окрестностях. Однако, в отличие от ОВР, веса для интерполяции в пределах
окрестностей выбираются с целью минимизации дисперсии оценки для всех комбинаций
отсчетов высоты. Эта дисперсия может быть получена непосредственно из модели, по
которой была прежде создана вариограмма.
Кригинг существует в двух основных формах. Общий (universal) кригинг, чаще всего
применяется, когда поверхность оценивается по нерегулярно распределенным отсчетам при
наличии тренда (условие, называемое нестационарностью). Ординарный (ordinary) кригинг
135
является элементарной формой и предполагает, что данные стационарны (не имеют тренда),
изотропны и собраны через равные интервалы. Наиболее часто локальный кригинг
используется для поиска точечных оценок на основе других точечных данных.
Ординарный кригинг по своей сути является лишь улучшением метода ОВР, в
котором учитываются не только расстояния от интерполируемой точки до исходных, но и
расстояния между самими исходными точками так, что веса более близких друг к другу
исходных точек уменьшаются. Этот метод превосходит простой метод ОВР именно тогда,
когда точки расположены с неравными интервалами, благодаря учету пространственной
корреляции исходных данных. Разработан также вариант метода, уменьшающий объем
вычислений в случае интерполяции многих точек при размещении исходных точек в узлах
регулярной сетки, он называется блочным кригингом (block kriging). Метод позволяет также
учитывать анизотропность, в этом случае вариограмма аппроксимируется функцией двух
независимых аргументов.
Кригинг часто дает довольно точные оценки пропущенных значений, но эта точность
обходится ценой времени и вычислительных ресурсов. Но даже при этом кригинг имеет еще
одно преимущество перед другими методами интерполяции, он не только дает
интерполированные значения, но также и оценку возможной ошибки этих значений. Это
может навести на мысль, что данный метод следует применять повсеместно, но увы. Когда
мы имеем дело с большим уровнем локального шума из-за ошибок измерений или большие
вариации высоты между отсчетами, в данном методе становится трудным построение кривой
полудисперсии. А в таких условиях результаты кригинга будут не лучше, чем полученные
другими методами.
В векторных моделях данных (чаще всего TIN) процесс интерполяции проще всего
выполняется выборкой точек с их значениями высоты и преобразованием их в точечную
матрицу высот.
В растровых покрытиях значения высоты обычно соотносятся с точками,
расположенными внутри каждой ячейки (например, в центре). Для интерполяции мы можем
использовать именно эти точки и действовать по одному из описанных выше методов. В
этом случае интерполируемым ячейкам растра присваиваются значения высоты, полученные
для представляющих их точек. Если ваша ГИС не содержит нужного алгоритма, то, как
правило, вы можете преобразовать точечные покрытия в форму, понимаемую
специализированным программным обеспечением, рассчитанным на работу с
пространственными данными. Затем его выходные данные могут быть преобразованы
обратно для дальнейшего анализа внутри ГИС.
ПРИМЕНЕНИЕ ИНТЕРПОЛЯЦИИ
Интерполяция полезна для создания изолиний, описывающих поверхности. Она
может также использоваться для отображения поверхности средствами блок-диаграмм или
карт с отмывкой рельефа. Но для чего еще может использоваться интерполяция? Допустим,
что вы планируете жилую застройку и не хотите попасть в зону наводнений, но у вас нет
карты, показывающей границы этой зоны. При этом вы знаете, что максимальный уровень
наводнений за сто лет составил 60 метров над уровнем моря. У вас также имеются заметки о
нескольких прежних участках строительства, и они включают данные высот для каждого
построенного дома. Изобразив данные на карте местности, вы можете использовать
интерполяцию для оценки высот вашего участка. По этим данным вы сможете начертить
изолинию, показывающую зону наводнений за 100 лет, и, просто сравнив ваше
местоположение с ней, узнаете, нужно ли менять место.
Теперь предположим, что вы прокладываете шоссе по не нанесенной на карту
территории и не можете начать строительство, не зная среднего градиента. Вы можете
создать карту поверхности тренда, чтобы показать общий характер уклона. Или, положим,
136
вы являетесь горным инженером, пытающимся определить общий тренд рудного
месторождения на основе информации из множества кернов, показывающих вершину и дно
залежи. Метод интерполяции поверхности тренда даст информацию о толщине рудного слоя
и его уклона под землей. Кроме того, метод кригинга окажется полезным в оценке качества
рудного слоя, так как рудные пласты хорошо описываются регионализованными
переменными.
На самом деле, существует множество применений интерполяции в различных
областях. Если вы хотите предсказать изменения состава почвы вдоль наклонной
поверхности, если исследуете тенденции в растительном покрытии на удалении от
источника воды, или если вы интересуетесь тенденциями изменения численности
населения на большой территории, исходя из выборочных данных за прошедшие
десятилетия, то все эти виды анализа требуют какого-либо вида интерполяции. О чем вам
следует помнить, так это о том, что интерполяция является, по сути, предсказательной
моделью.
ПРОБЛЕМЫ ИНТЕРПОЛЯЦИИ
Мы рассмотрели несколько методов интерполяции, при выполнении которых должны
учитываться следующие четыре фактора:
1. Число исходных точек
2. Положения исходных точек
3. Проблема седловых точек
4. Область, содержащая точки данных
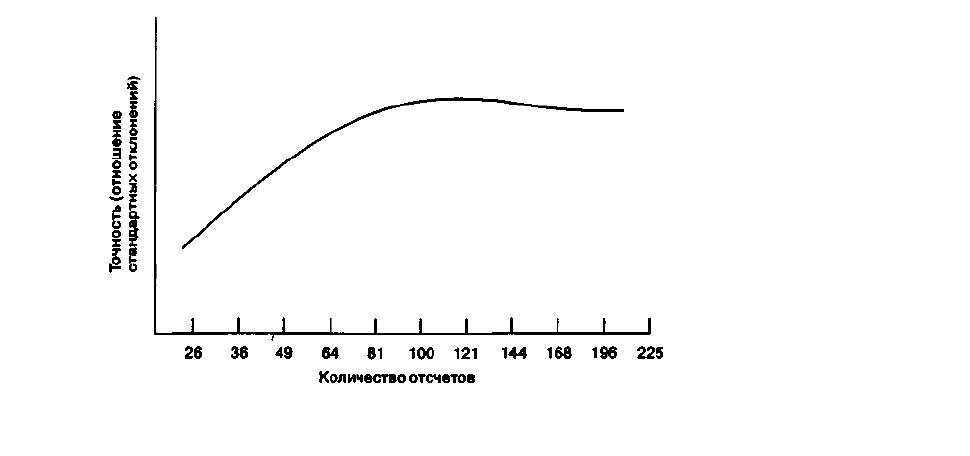
Рисунок 17.10. Точность карты изолиний в зависимости от числа точек данных.
Характерная кривая
гипотетического отношения между числом точек и точностью карты.
В общем случае можно сказать, что чем больше исходных точек мы имеем, тем более
точной будет интерполяция и тем с большей вероятностью интерполированная поверхность
будет хорошей моделью. Однако, существует предел числу отсчетов, которые могут быть
сделаны для любой поверхности. Постепенно достигается момент снижения отдачи: большее
количество точек не улучшает существенно качество результата, но лишь увеличивает время
вычислений и объем данных. В некоторых случаях избыточные данные могут приводить к

137
необычным результатам, поскольку группы точек в областях, где данные могут быть легко
собраны, могут создать неравномерное представление поверхности, и, следовательно,
неодинаковую точность. Другими словами, большее число точек не всегда улучшает
точность: Рисунок 17.10 показывает, что при некотором количестве точек точность на самом
деле снижается.
Конечно, количество исходных точек часто является функцией формы поверхности.
Чем сложнее поверхность, тем больше точек данных требуется. А для важных объектов,
таких как впадины и долины рек, требуются дополнительные точки данных, чтобы
гарантировать представление необходимой подробности. Вдобавок, хотя положение точек
измерения друг относительно друга имеет влияние на точность интерполяции, сама
зависимость не является линейной (Рисунок 17.11).
Рисунок 17.11. Распределение отсчетов и точность изолиний.
Характеристическая кривая гипотетического
отношения между расстоянием между точками данных и точностью контурной карты.
Проблема седловой точки (saddle-point problem), называемая иногда проблемой
альтернативного выбора, возникает тогда, когда две точки одной пары диагонально
противоположных Z-значений, образующих прямоугольник, расположены ниже, а две точки
другой диагональной пары находятся выше того значения, которое пытается найти алгоритм
интерполяции (Рисунок 10.12а)*. Это обычно случается только при линейной интерполяции,
но когда это происходит, программа встает перед лицом двух возможных решений одного
вопроса: где провести изолинию (Рисунок 10.12). Простым способом решения этой
проблемы является помещение среднего от двух, полученных по диагоналям,
интерполированных значений в точке пересечения диагоналей (Рисунок 10.13).
Рисунок 10.13. Решение проблемы седловой точки.
Решение использует среднее значение, помещенное точно в

138
центр.
Последняя проблема, которая должна учитываться при интерполяции, является общей
для операций в ГИС, имеющих дело с областью, в пределах которой собираются точки
данных. А именно, чтобы интерполяция работала должным образом, интерполируемые точки
должны быть окружены точками с известными значениями со всех сторон. Но если мы, как
часто бывает, выбираем для анализа всю область исследования и используем ту же область
для выполнения интерполяции, то вскоре нам приходится интерполировать точки вблизи
границы области. И с приближением к границе алгоритм интерполяции вынужден
использовать исходные точки только с трех и даже двух сторон от интерполируемой. Как мы
видели, наилучшие результаты интерполяции достигаются тогда, когда мы можем расширять
окрестность по всем направлениям для выбора исходных точек и определения весов. В
отсутствие этих окружающих точек алгоритм будет использовать то, что есть, допуская
систематическую ошибку вдоль границы.
139
Лекция № 18 АНАЛИЗ СТАТИСТИЧЕСКИХ ПОВЕРХНОСТЕЙ
Как было сказано выше, основным методом отображения информации о поверхности
является использование изолиний, которые проводятся через установленные интервалы.
Выбранный интервал позволяет передавать форму поверхности, при этом мы полагаем, что
высота между контурными линиями изменяется непрерывным образом, так как считаем
саму поверхность непрерывной. Мы также полагаем, что интервал выбирается таким, чтобы
отобразить форму поверхности наилучшим образом. Большинство растровых и векторных
ГИС позволяет изменять этот интервал и даже преобразовывать область каждого интервала
в плоскую поверхность. Для простоты мы будем называть эту группу методов
нарезкой
(slicing) и представлять их выполнение как множественное рассечение поверхности
по
горизонтали острым ножом.
Нарезка может быть просто делом выбора другого контурного интервала,
позволяющего по-иному взглянуть на особенности рельефа поверхности (Рисунок 10.15).
Например, мы могли бы увеличить интервал между изолиниями, чтобы выявить общую
форму объектов без избыточных подробностей. Хорошая визуализация дает
представление о тенденциях без необходимости реального вычисления поверхностного
тренда. И наоборот, чтобы увидеть больше деталей, мы можем уменьшить вертикальный
интервал между изолиниями. Конечно же, сами исходные данные должны быть при этом
достаточно подробными.
В более общем случае функция нарезки могла бы правильнее называться функцией
окрестности. Здесь же мы ее рассматриваем потому, что по своему выполнению она тесно
связана с интерполяцией. Этот подход подразумевает, что проведением контурных линий на
заданных интервалах мы по сути сводим непрерывную поверхность к дискретной,
ступенчатой поверхности. Почему же мы низводим наши данные из непрерывных в
дискретные? Возможно, следующий пример поможет ответить на этот вопрос.
Допустим, вы работаете в консалтинговой фирме с контрактом, заключенным с
правительством другой страны. И вас попросили определить подходящие виды
землепользования для большого участка земли на основе комбинации характеристик почвы и
классов высот. Классы высот выбирались вместо классов уклона отчасти потому, что
большинство земельных изысканий учитывают уклон в характеристиках почвы, отчасти
потому, что советники клиента по сельскому хозяйству знают, что некоторые растения
растут на одних высотах лучше, чем на других. Исходя из требований к высоте различных
сельскохозяйственных культур (таковых, скажем, — пять) вы можете разделить поверхность
на пять высотных регионов нарезкой четырьмя плоскостями.
После выполнения нарезки эти регионы могут быть переклассифицированы по их
влиянию на те пять культур. Теперь у вас есть пять групп, основанных на высотных классах
с учетом воздействия последних на сельхозкультуры, названные "высоты для культуры 1","
высоты для культуры 2" и т.д. Таким образом, вы преобразовали данные поверхности,
представленные в шкале отношений (непрерывные), в данные номинальной шкалы
(дискретные), исходя из воздействия высоты на культуры. Как мы увидим в Главе 12, эти
результаты могут быть объединены с другими покрытиями для принятия решений о том, где
какие культуры должны быть посажены.
ОБЪЕМЫ, ОГРАНИЧИВАЕМЫЕ ПОВЕРХНОСТЯМИ
Хотя интерполяция полезна для работы с поверхностями, она может также
применяться к множеству других задач, связанных с вычислением объемов под объектами на
поверхности, или объемов материала, связанного с выемками и заполнением (как, например,

140
при изъятии руды и последующем заполнении для сохранения плоской поверхности). Во
всех таких случаях требуется знание двух граничных поверхностей: верхней и нижней.
Применив нарезку или методы интегрального исчисления, мы можем определить объем.
Давайте посмотрим, как это делается.
Если бы мы имели цилиндрический объект с площадью основания, скажем, 150 кв.м и
высотой два метра, то его объем составил бы 2 × 150 = 300 кубометров. Но большинство
измеряемых объектов имеют сложную форму.
Рассмотрим, например, дождевые осадки. Пусть у нас есть 15 измерителей,
разбросанных по площади в 100 кв.км (1000 000 кв.м), и после сбора данных мы хотим
определить общее количество осадков в каждом месте за целый год. Из-за изменчивости
осадков, мы можем получить значения, скажем, от 50 см до 150 см. Взяв среднюю величину
осадков (100 см), мы можем представить себе плоскую поверхность, и тогда получим объем
в 1 м × 1 000 000 кв.м = 1 000 000 кубометров воды.
Рисунок 17.16. Метод ординат.
Использование метода ординат для определения объема воды в регионе.
Но допустим, что нам нужно более точное определение объема осадков. Для этого мы
можем использовать так называемый метод ординат (method of ordinates). Рисунок 10.16
показывает, какой работает. Сначала мы записываем координаты каждого измерителя
осадков и создаем матрицу высот, точно так же, как мы поступали бы в случае топографии.
Затем мы используем подходящий метод интерполяции для создания поверхности и режем
ее на части равной толщины (т.е. проводим изолинии). Если мы примем, что стенки
полученных слоев вертикальны, то сможем выполнить тот же простой расчет объема для
каждого из них. Сложив эти объемы, мы получим более точное значение объема осадков,
чем в прежнем случае, предполагавшим одинаковое среднее количество осадков по всей
территории. Поскольку оба этих метода исходят из того, что наши объемы ограничены
вертикальными стенками, вычисление объема очень просто как в растровой, так и в
векторной модели. Для каждого слоя нарезки мы просто перемножаем значения площади и
глубины.
Конечно, желательно иметь возможность определять объем как можно точнее. И
увеличив число слоев нарезки, вы можете значительно улучшить точность расчета.
Теоретически, можно уменьшать толщину слоев до бесконечности, что и делается в
интегральном исчислении.
Помните, что расчеты объема холма и объема озера по сути одинаковы в том, что
одна из ограничивающих поверхностей является плоской. Конечно, это несколько упрощает
