Лекции - Математические основы моделирования
Подождите немного. Документ загружается.


Математические основы моделирования дискретных систем
Введение
Моделирование дискретных систем (ДС) позволяет изучать свойства и
закономерности, присущие процессам, протекающим в ДС, в частности в вычислительных
системах, с различной структурно-функциональной организацией. Эти процессы в общем
случае являются недетерминированными и описываются в терминах теории вероятностей.
Исследование ДС проводится на математических моделях, отражающих как структуру,
так и процессы, протекающие в соответствующих системах. Модели ДС со
стохастическим характером функционирования строятся на основе моделей теории
массового обслуживания, анализ которых во многих случаях проводится методами теории
Марковских случайных процессов.
В настоящем пособии рассматриваются математические основы моделирования
стохастических ДС. В первом разделе приводятся необходимые сведения из теории
вероятностей, описываются основные законы распределения случайных величин и
рассматриваются наиболее важные числовые характеристики. Второй раздел посвящен
рассмотрению такого класса случайных процессов, как Марковские случайные процессы,
как с дискретным, так и с непрерывным временем. При этом особое внимание уделяется
частному случаю Марковских случайных процессов в виде процессов размножения и
гибели, которые тем не менее находят широкое применение при анализе ДС со
стохастическим характером функционирования.
Необходимые сведения теории вероятностей подробно приводятся в работах [1,2].
С наиболее доступным полным изложением задач и методов теории Марковских
случайных процессов можно ознакомится в литературе [3,4,5]. Кроме того, в работах [4,5]
подробно рассматриваются вопросы применения Марковских случайных процессов в
качестве моделей стохастических систем различной организации.
Раздел 1
Элементы теории вероятностей
1.1. Понятие вероятности и случайной величины.
Теория вероятностей занимается описанием случайных событий. Под случайным
событием понимается всякий факт, лишенный преднамеренности и регулярности, или
другими словами, факт, который может произойти или не произойти в результате какого-
нибудь опыта. Каждое из случайных событий обладает той или иной степенью
возможности. Для количественного сравнения между собой событий по степени их
возможности с каждым событием связывается определенное число, называемое
вероятностью события. Более возможному событию соответствует большая вероятность.
Таким образом, вероятность события есть численная мера степени объективной
возможности этого события.
Предположим, что рассматривается некоторый опыт или явление, в котором в
зависимости от случая происходит или не происходит некоторое событие А. Если условия
опыта могут быть воспроизведены многократно, так что в принципе будет осуществима
целая серия одинаковых и независимых друг от друга испытаний, то вероятность события
А, обозначаемая через Рr[A], может быть вычислена по формуле:
Рr[A] = n/N,
где N - общее число взаимно исключающих друг друга исходов; n - число исходов,
которые приводят к наступлению события A.
Вероятность любого события А должна удовлетворять условию:
0
Pr[A]
1.
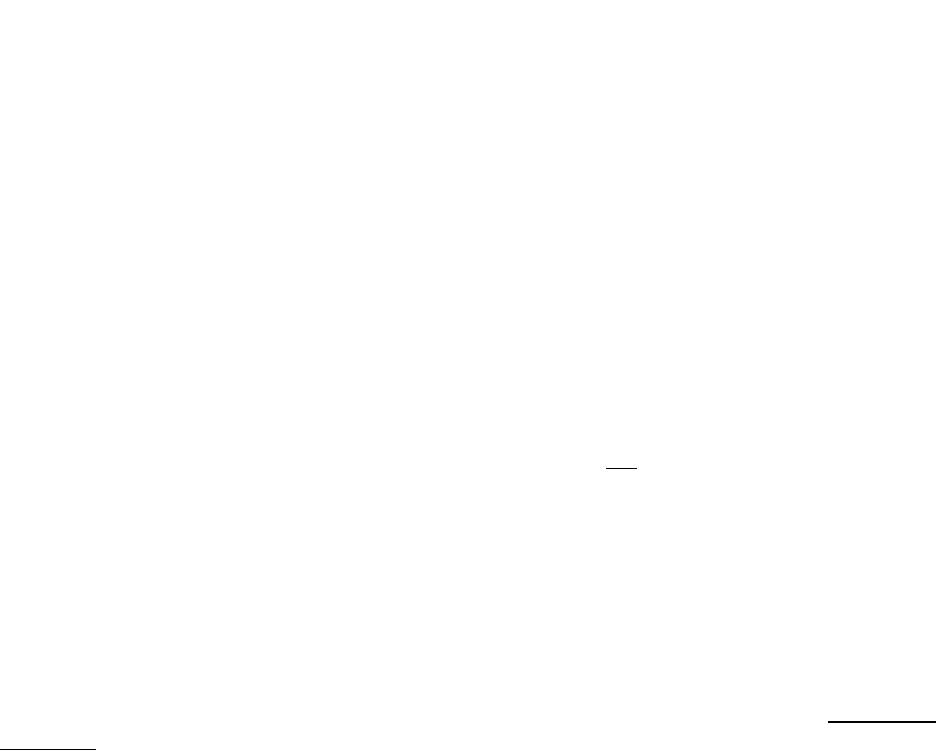
Если Рr[А]=0, то событие А называется невозможным или нулевым (0) событием, а
событие, для которого Рr[А]=1, называется достоверным.
Множество событий {А
1
, А
2
,..., А
n
} образует полную группу событий, если в
результате опыта должно непременно появиться хотя бы одно из них. Для полной группы
событий справедливо условие:
Рr[A
1
]+Рr[A
2
]+...+Рr[A
n
]=1.
События А и В называются несовместными или взаимоисключающими, если в
результате опыта они не могут появиться одновременно (вместе), и для таких событий
справедливо:
Рr[АВ]=Рr[0]=0 и Pr[A
B]=Pr[A]+Pr[B] .
События А и В называются независимыми, если появление одного из них не
зависит имело место или нет другое событие. Для таких событий
Pr[AB]=Pr[A]Pr[B].
Такое равенство в виде произведения справедливо и для большего количества
независимых событий.
Условная вероятность события А, если известно, что наступило событие В,
обозначаемая через Pr[A|B], определяется как
Pr[A|B]=Pr[AB]/Pr[B], если Pr[B]
0.
Пусть {A
1
, A
2
, ..., A
n
} - множество несовместных событий, образующее полную
группу событий. Теорема о полной вероятности связывает вероятность события В с
данным множеством:
Pr[B]=
;]Pr[
1
n
i
i
BA
это означает, что событие В наступает совместно точно с одним из взаимно несовместных
исчерпывающих событий A
i
, i=1,n. Однако из определения условной вероятности можно
написать
Pr[A
i
B]=Pr[A
i
|B]Pr[B]=Pr[B|A
i
]Pr[A
i
];
это дает вторую важную форму теоремы о полной вероятности, а именно:
Pr[B]=
n
i
ii
AAB
1
]Pr[]|Pr[
.
Одним из основных понятий теории вероятностей является понятие о случайной
величине. Случайной величиной называется величина, которая может принять то или иное
значение, неизвестное заранее. Случайные величины могут быть двух видов:
1) дискретные случайные величины (ДСВ), принимающие только отдельные друг
от друга значения из дискретного (конечного или счетного) множества;
2) непрерывные случайные величины (НСВ), которые могут принимать любые
значения из некоторого промежутка.
Примерами ДСВ являются: число покупателей в магазине, количество обращений к
серверу, число процессорных операций при выполнении программы и т.д.
Примерами НСВ являются: время выполнения программы, интервалы прихода
покупателей в магазин; значение температуры в течение дня и т.д.
Случайные величины часто обозначают большими буквами (например X), а их
возможные значения - соответствующими малыми буквами: x
1
, x
2
, ..., x
n
.
(1.1)
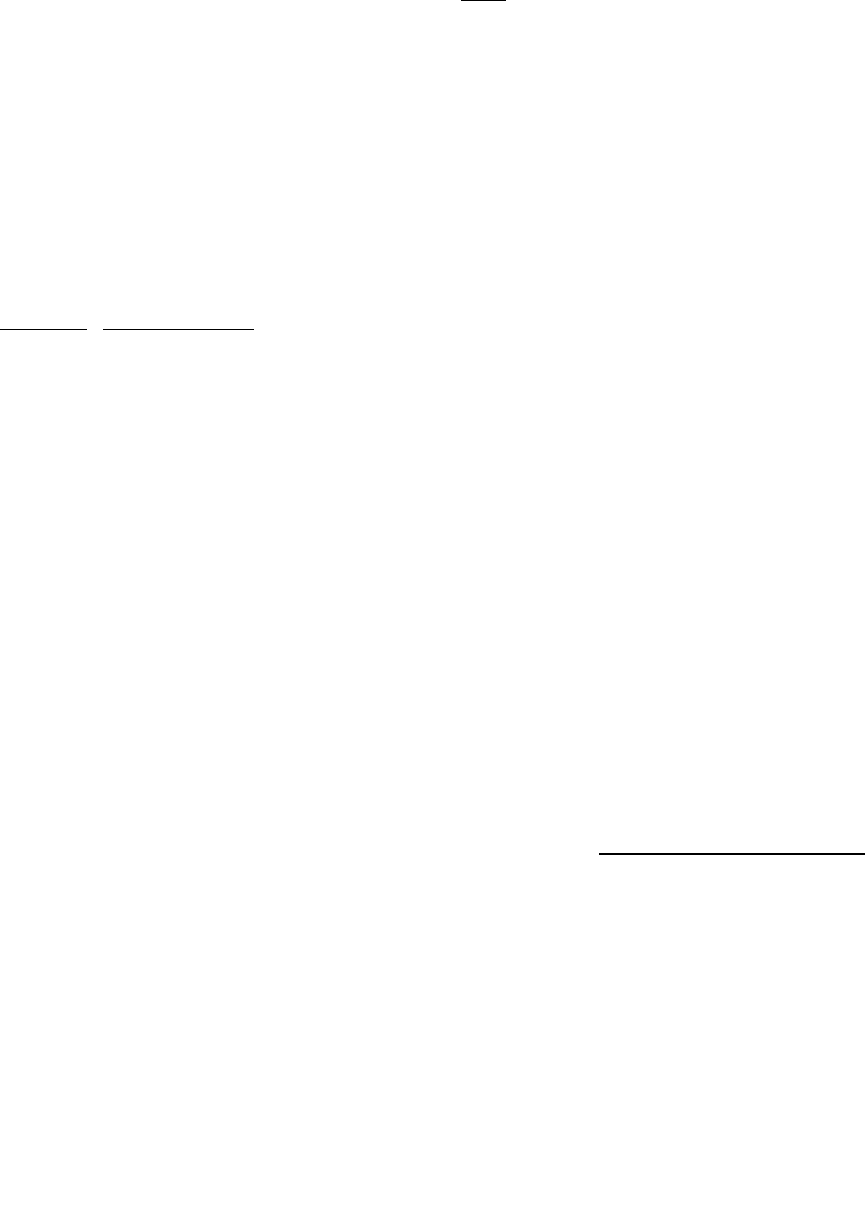
1.2. Законы распределения случайных величин.
Рассмотрим дискретную случайную величину Х с возможными значениями х
1
, x
2
,
..,
х
n.
Величина Х может принять каждое из этих значений с некоторой вероятностью.
Вероятность того, что случайная величина Х примет значение х
i
обозначим через P
i
, то
есть:
P
i
=Pr{X=x
i
}, i= 1,n.
Если в результате опыта величина Х принимает только одно из этих значений, то
имеем полную группу несовместных событий, и сумма вероятностей всех возможных
значений случайной величины равна единице:
n
i
i
P
1
1
.
Эта суммарная вероятность каким-то образом распределена между отдельными
значениями. Случайная величина будет полностью описана с вероятностной точки зрения,
если задано это распределение, то есть установлен так называемый закон распределения.
Законом распределения случайной величины называется всякое соотношение,
устанавливающее связь между возможными значениями случайной величины и
соответствующими им вероятностями. При этом про случайную величину говорят, что
она подчинена данному закону распределения.
Закон распределения дискретной случайной величины может быть задан одним из
следующих способов:
1) аналитически в виде математического выражения, отражающего зависимость
вероятности от значения случайной величины;
2) таблично в виде ряда распределения случайной величины, в котором
перечислены возможные значения случайной величины и соответствующие им
вероятности;
3) графически в виде многоугольника распределения, при котором по оси абсцисс
откладываются возможные значения случайной величины, а по оси ординат - вероятности
этих значений.
Для непрерывной случайной величины, поскольку НСВ имеет бесчисленное
множество возможных значений, сплошь заполняющих некоторый промежуток, каждое
отдельное значение обычно не обладает никакой отличной от нуля вероятностью. Для
описания НСВ Х удобно воспользоваться не вероятностью события X=x, а вероятностью
события X
x, где х - некоторая текущая переменная. Вероятность этого события,
очевидно, является фикцией от переменной х и называется функцией распределения
случайной величины Х. Обозначим функцию распределения через F(x). Тогда:
F(x)=Pr{X
x}.
Функцию распределения F(x) называют иногда интегральной функцией
распределения или интегральным законом распределения. Функция распределения
полностью характеризует случайную величину с вероятностной точки зрения и является
одним из способов задания закона распределения.
Функция распределения обладает следующими свойствами:
1) функция распределения - неотрицательная функция, то есть F(x)
0;
2) функция распределения F(x) - неубывающая функция, то есть, если x
2
x
1
, то
F(x
2
)
F(x
1
);
3) на минус бесконечности функция распределения равна нулю, а на плюс
бесконечности - единице, то есть F(-
)=0, а F(+
)=1;
(1.2)
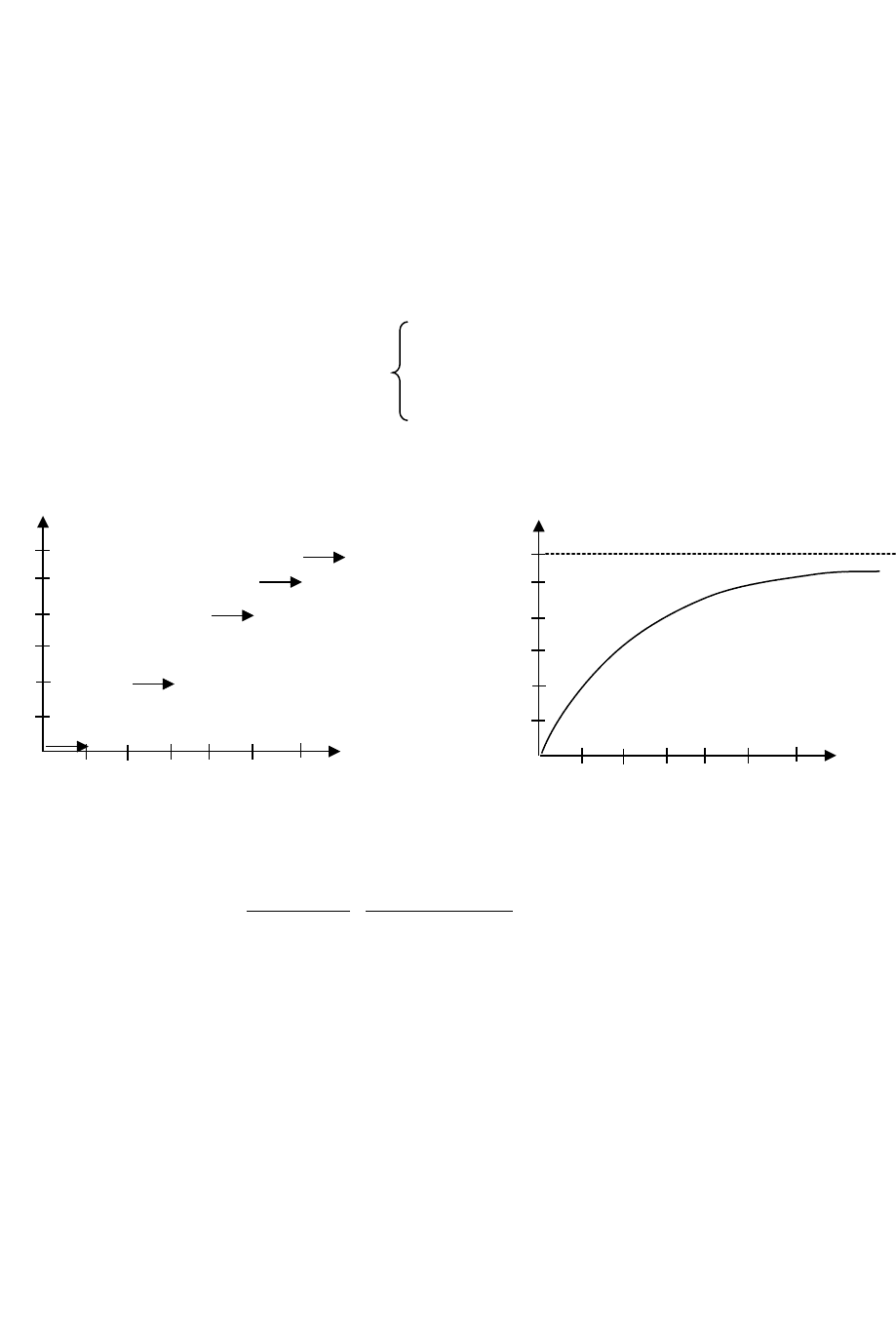
4) вероятность попадания случайной величины X в отрезок [x
1
, x
2
] равна
приращению функции распределения на этом отрезке, то есть Pr{x
1
x
x
2
}= =F(x
2
)-
F(x
1
);
5) функция распределения F(x) сама является случайной величиной,
распределенной равномерно на отрезке [0,1].
Если случайная величина определена в области положительных значений, что
имеет место для большинства величин, используемых в теории моделирования
дискретных систем, ее функция распределения равна нулю на всем промежутке от минус
бесконечности до нуля: F(x)=0 при x
0.
Следует отметить, что функция распределения является универсальной
характеристикой случайной величины и существует как для непрерывных, так и для
дискретных величин. Функция распределения для ДСВ X, принимающей значения x
1
,
x
2
, ..., x
n
, ... при условии, что x
1
x
2
...
х
n
..., может быть определена в виде:
F(x)=Pr{X
x}= (1.3)
На рис. 1.1 и 1.2 приведены примерные графики функций распределения
соответственно дискретной и непрерывной случайных величин, определенных в области
положительных значений.
F(x) F(x)
l
n+1
1
l
n
l
n-1
. …
. …
l
2
l
1
0 x
1
x
2
x
3
...x
n-1
x
n
x
n+1
x 0 x
Pис. 1.1. Функции распределения ДСВ. Pис.1.2. Функции распределения НСВ.
Для вероятностного описания непрерывной случайной величины наряду с
функцией распределения широко используется другая форма задания закона
распределения в виде плотности распределения, которая обозначается через f(х) и
определяется как производная от функции распределения, то есть f(x)=F
/
(x). Иногда
плотность распределения f(х) называют плотностью вероятности или дифференциальной
функцией (законом) распределения случайной величины.
Функция и плотность распределения случайной величины однозначно связаны
между собой. В частности, функция распределения определяется через плотность
распределения равенством:
F(x)=
x
dyyf )(
.
Для плотности распределения можно отметить следующие свойства:
1. плотность распределения есть неотрицательная функция: f(х) >0;
2. интеграл от плотности распределения в области определения случайной величины
равен единице:
;1)(
dxxf
0 при x<x
1
;
n
i
i
P
1
при x
n
x< x
n+1
.
n
i
in
Pl
1
3. вероятность попадания случайной величины X в отрезок [x
1
, x
2
] равна интегралу от
плотности распределения на этом отрезке:
Pr{x
1
x
x
2
}=
2
1
)(
x
x
dxxf
.
Далее рассмотрим наиболее широко используемые в теории моделирования
дискретных систем законы распределения случайных величин.
Для дискретных случайных величин таковыми являются:
1) закон распределения Пуассона;
2) геометрический закон распределения.
Распределение Пуассона. Случайная величина X распределена по закону Пуассона, если
вероятность того, что она примет целочисленное значение k, выражается формулой:
P
k
=Pr{X=k}=
!k
a
k
e
-a
, k=0, 1, 2, ...,
где а>0 и называется параметром распределения Пуассона. Выражение (1.4) представляет
собой аналитический способ описания закона распределения.
На рис. 1.3 приведены многогранники распределения Пуассона, соответствующие
различным значениям параметра а.
Геометрическое распределение. Распределение дискретной случайной величины X=k вида
P
k
=Pr{X=k}=
(1-
)
k
, k=0, 1, 2, ...,
где
- параметр распределения (0<
<1), называется геометрическим.
Многоугольники геометрического распределения, соответствующие различным
значениям параметра
, приведены на рис. 1.4.
Распределение (1.5) может быть записано в несколько ином виде, если параметр
заменить параметром
=1-
:
P
k
=
k
(1-
), k=0, 1, 2, ..., где 0<
<1.
P
k
P
k
0.5 a=0.5 0.5
=0,9
0.4 0.4
0.3 a=1 0.3
0.2 a=5 0.2
=0,5
0.1 0.1
=0,1
0 2 4 6 8 10 k 0 2 4 6 8 10 k
Рис. 1.3. Распределение Пуассона. Рис. 1.4. Геометрическое распределение.
В случае непрерывных случайных величин наиболее широко используемыми
законами распределения являются:
1) экспоненциальное распределение;
2) распределение Эрланга;
3) гиперэкспоненциальное распределение;
4) равномерное распределение.
Экспоненциальное распределение. Распределение непрерывной случайной величины с
функцией распределения
F(t)=1-e
-
t
, t
0
(1.4)
(1.5)
(1.6)
(1.7)
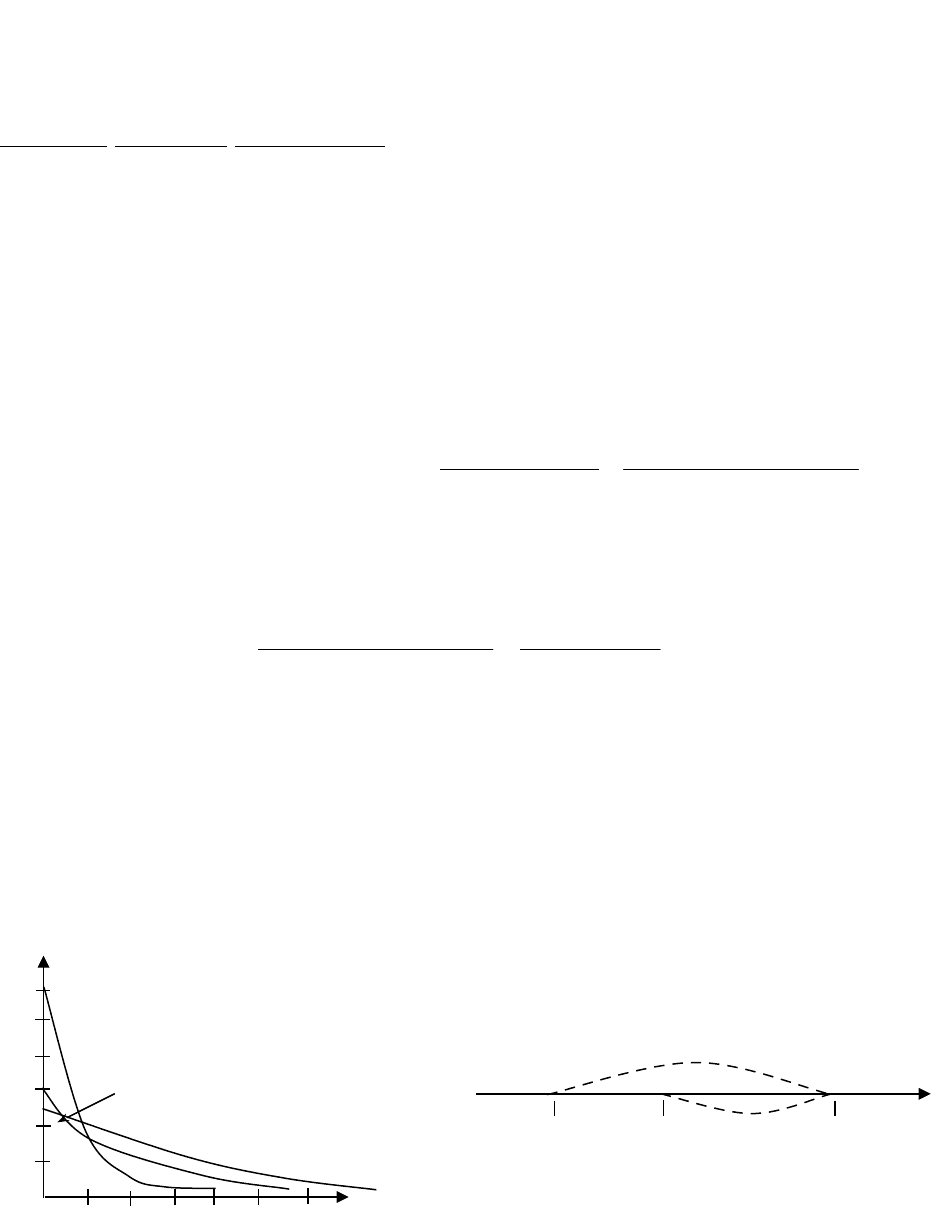
называется экспоненциальным распределением. Здесь
>0 и называется параметром
экспоненциального распределения.
Плотность экспоненциального распределения
f(t)=F
/
(t)=
e
-
t
, t
0.
Графики плотности распределения, соответствующие различным значениям
параметра
, приведены на рис. 1.5.
Экспоненциальное распределение обладает замечательным свойством, названным
свойством отсутствия последействия. Это свойство значительно упрощает аналитическое
моделирование систем со случайным характером функционирования. Как говорит уже
само название, прошлая история экспоненциально распределенной случайной величины
не играет роли в предсказании ее будущего. Более точно имеется в виду следующее.
Допустим, что длительность телефонного разговора
является случайной величиной,
распределенной по экспоненциальному закону (1.6). Пусть t=0 - момент начала разговора
(рис.1.6), а t=t
1
- случайная точка на временной оси, соответствующая моменту окончания
разговора. Предположим теперь, что прошло некоторое время t
0
, в течение которого
продолжался телефонный разговор. Тогда
’=t
1
-t
0
- случайное время, которое осталось до
окончания разговора. Возникает вопрос: по какому закону распределена случайная
величина
’? Для ответа на этот вопрос проведем следующие вычисления:
F
’
(t)=Pr{
’
t}=Pr{
t+t
0
|
>t
0
}=
}Pr{
}Pr{
0
00
t
ttt
=
}Pr{
}Pr{}Pr{
0
00
t
ttt
.
Здесь мы последовательно воспользовались соотношением между
и
’ ,
выражением (1.1) для условной вероятности и четвертым свойством функции
распределения. Согласно равенству (1.6) имеем:
t
t
ttt
t
ttt
e
e
ee
e
ee
tF
1
)1(1
)1()1(
)(
0
00
0
00
)()(
.
Этот результат показывает, что оставшееся время разговора при условии, что уже
разговаривали в течение времени t
0,
распределено по такому же закону, что и безусловная
длительность разговора. Это дает основание считать, что время до окончания разговора не
зависит от того, сколько времени прошло с момента его начала. Другими словами,
будущее экспоненциально распределенной случайной величины не зависит от прошлой
истории этой величины, и соответствующее распределение остается неизменным во
времени. Экспоненциальное распределение является единственным непрерывным
распределением, обладающим этим свойством. В случае дискретных случайных величин,
единственным распределением с таким же свойством является геометрическое
распределение.
f(t)
2
1
0 1 2 3 4 5 6 t
Рис 1.5. Плотность экспоненциального
распределения.
Рис 1.6. Пояснение свойства отсутствия
последействия.
=1
=2
=0.8
0 t
0
’ t
1
t
Распределение Эрланга. Распределением Эрланга k-го порядка называется распределение,
описывающее непрерывную случайную величину, представляющую собой сумму k
независимых случайных величин, распределенных одинаково по экспоненциальному
закону с параметром
. Функция распределения и плотность распределения Эрланга
порядка k имеют вид:
F
k
(t)=1-e
-
t
1
0
!
)(
k
n
n
n
t
, t
0;
f
k
(t)=
)!1(
)(
1
k
t
k
e
-
t
, t
0,
где
и k - положительные параметры распределения, причем параметр k принимает
только целочисленные значения: k=1, 2, 3, ... . Таким образом, распределение Эрланга
является двухпараметрическим. Экспоненциальное распределение можно рассматривать
как частный случай распределения Эрланга при k=1. При k
распределение Эрланга
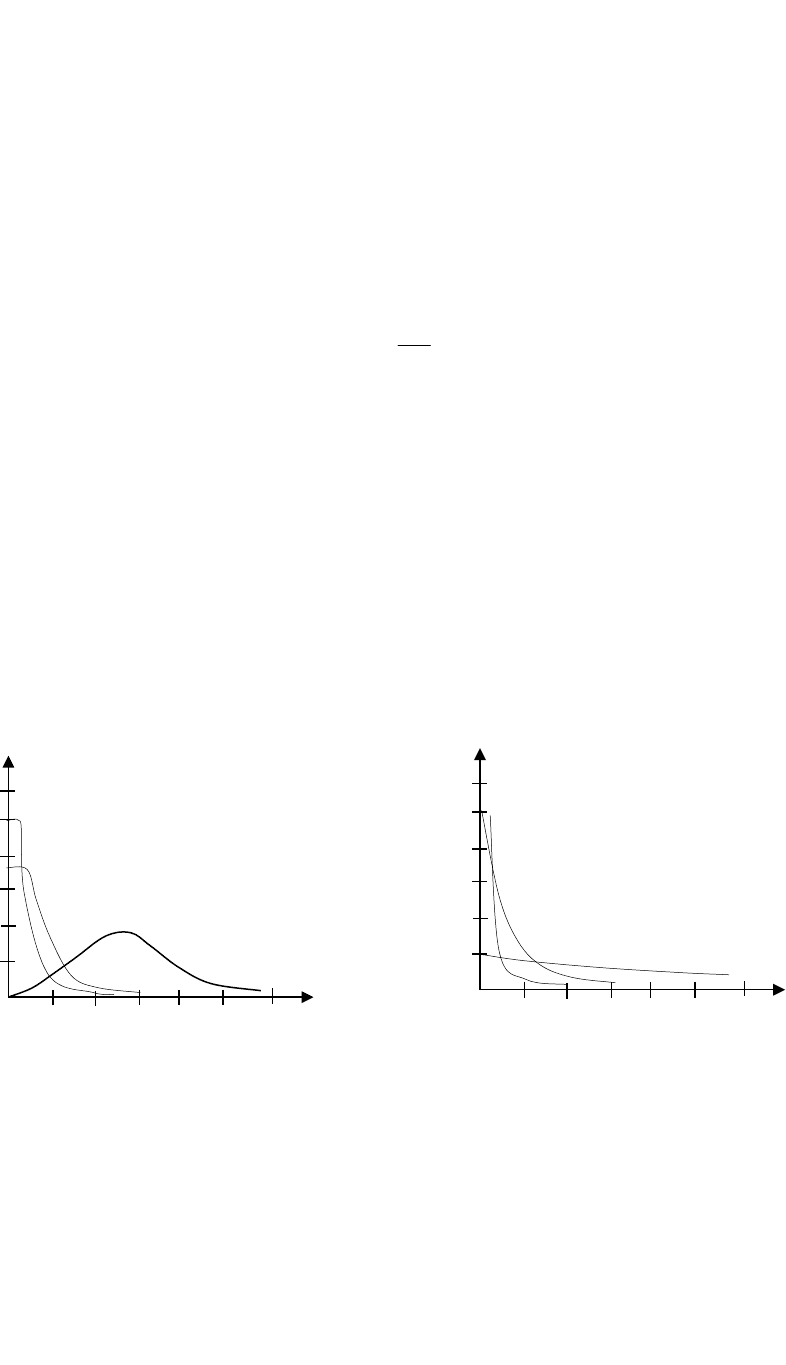
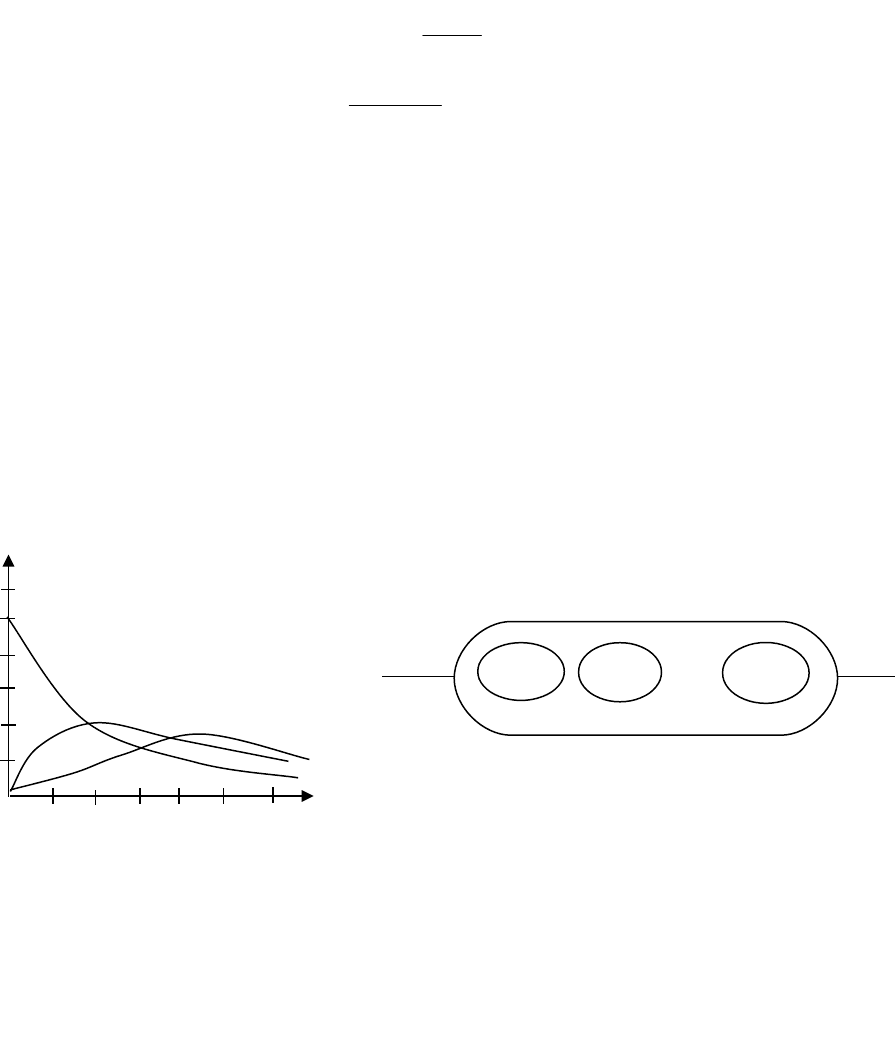
приближается к нормальному распределению. На рис. 1.7 приведены графики плотности
распределения Эрланга при различных значениях параметра k, а на рис. 1.8 - его
схематическое представление.
Гиперэкспоненциальное распределение. Гиперэкспоненциальным распределением
порядка k называется распределение, описывающее случайную величину, которая с
вероятностью P
1
распределена по экспоненциальному закону с параметром
1
, с
вероятностью P
2
- с параметром
2
,…, с вероятностью P
k
- с параметром
k
. При этом
параметр k принимает только целочисленные значения, а вероятности P
1
, P
2
, ..., P
k
удовлетворяют условию:
1
1
k
n
n
P
.
f
k
(t)
1
0.8 k=1 (
=1)
0.6
0.4
0.2
0 0.5 1.0 1.5 2.0 2.5 t
Рис 1.7. Графики плотности распределения
Эрланга порядка k.
Рис 1.8. Схематическое представление
распределения Эрланга порядка k.
Функция и плотность распределения гиперэкспоненциального распределения
порядка k имеют вид:
F
k
(t)=1-
t
k
n
n
n
eP
1
, t
0;
f
k
(t)=
t
n
k
n
n
n
eP
1
, t
0.
Нетрудно заметить, что приведенные функция и плотность распределения
представляют собой взвешенные суммы соответствующих функций и плотностей
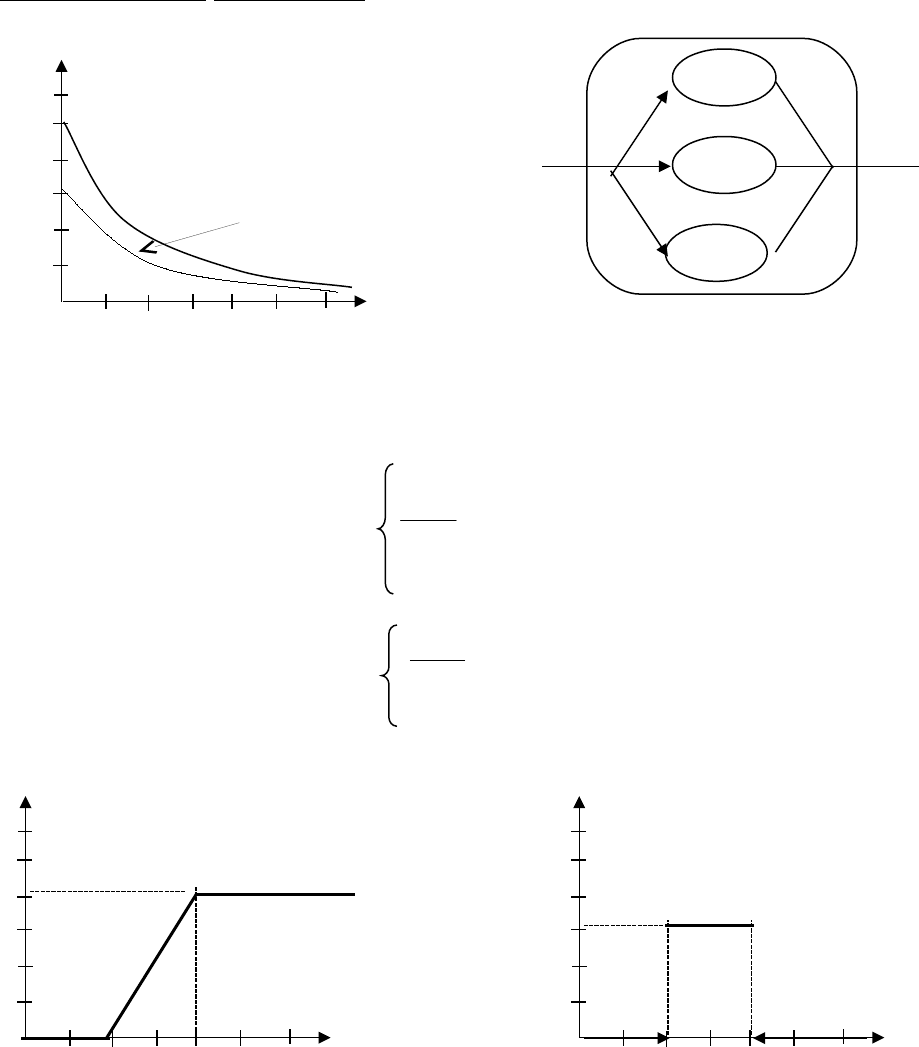
экспоненциальных распределений, составляющих гиперэкспоненту. На рис. 1.9
приведены графики плотности распределения гиперэкспоненциального распределения
при различных значениях k, а на рис. 1.10 - схематическое представление такого
распределения.
(1.10)
(1.11)
+ + ...+
ex
p
ex
p
ex
p
1 2 k
k=3
k=2
(1.9)
(1.8)
Гиперэкспоненциальное распределение является частным случаем
гиперэрланговского распределения, где составляющими его распределениями выступают
распределения Эрланга того или иного порядка.
f
k
(t)
k=1(
1
=1)
1
0.8
0.6
0.4
0.2
0 0.5 1.0 1.5 2.0 2.5 t
Рис 1.9. График плотности распределения
гиперэкспоненты.
Рис 1.10. Схематическое представление
гиперэкспоненты.
Равномерное распределение. Говорят, что непрерывная случайная величина распределена
равномерно на отрезке [a, b], если ее функция распределения имеет вид:
0 при x<a;
F(x)=
ab
ax
, если a
x
b;
1 при x>b.
При этом плотность распределения определяется выражением:
f(x)=
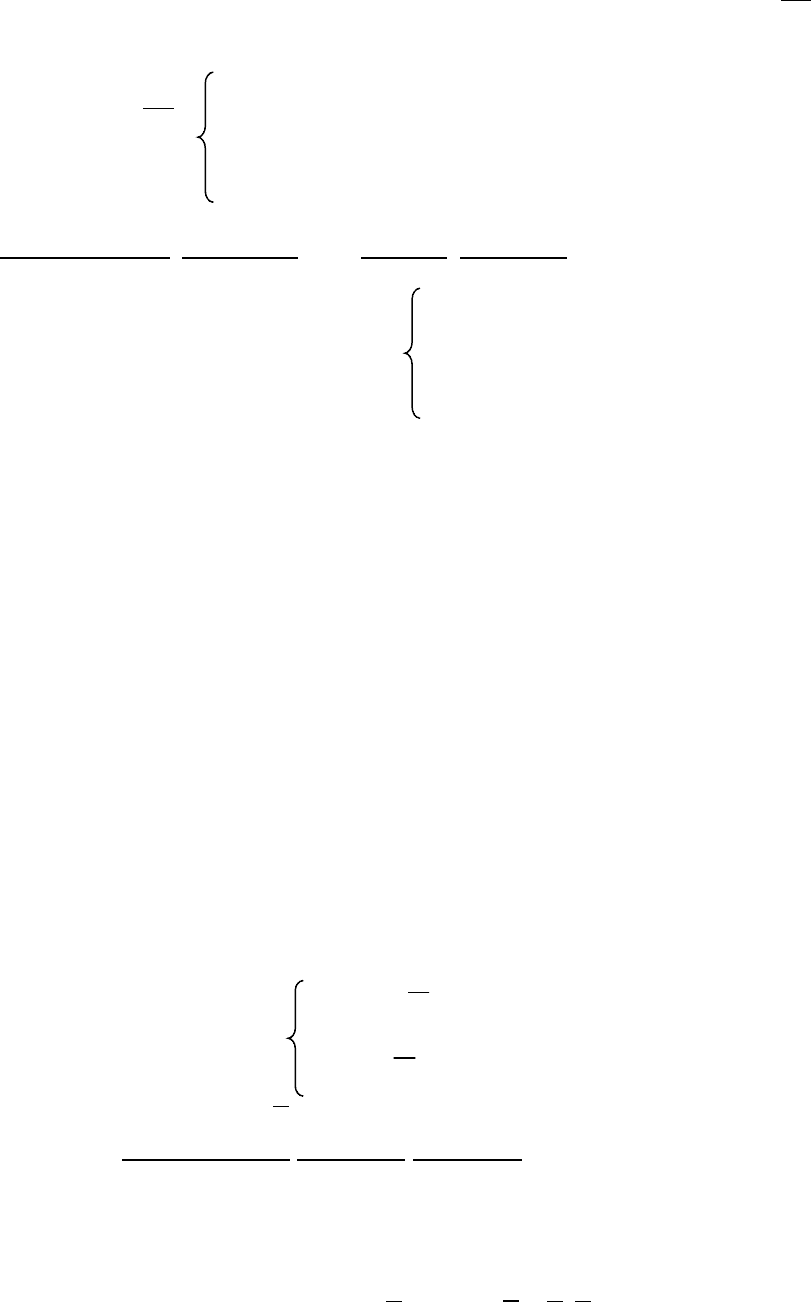
На рис. 1.11 и 1.12 приведены графики рассматриваемых функций.
При моделировании дискретных систем наибольшее применение находит частный
случай равномерного распределения, когда а=0 и b=1.
F(x) f(x)
1
a b x a b x
Рис 1.11. График функции распределения. Рис 1.12. График плотности распределения.
1.3. Числовые характеристики случайных величин.
Числовые характеристики позволяют выражать в сжатой форме наиболее
существенные особенности распределения случайной величины. В теории вероятности
используется большое количество числовых характеристик, имеющих различное
назначение и различные области применения. Из них наиболее часто используются
начальные и центральные моменты. С помощью числовых характеристик существенно
облегчается решение многих вероятностных задач, когда использование законов
распределения приводит к громоздким выкладкам и не позволяет получить результаты в
явном виде.
ab
1
при а
x
b;
0 при x<a и x>b.
1/(b-a)
(1.12)
(1.13)
...
...
exp 1
exp n
P
1
P
n
P
k
exp k
1
=0.8,
2
=0.4
P
1
=0.5, P
2
=0.5
Для того, чтобы дать общее определение моментов одновременно для дискретных
и непрерывных случайных величин, рассмотрим случайную величину X и предположим,
что она описывается вероятностями P
1
, P
2
, ..., P
m
ее возможных значений х
1
, х
2
,..., х
m
, если
Х - дискретная величина, и плотностью распределения f(x), если Х - непрерывная
случайная величина.
Начальный момент n-го порядка, обозначаемый через M[X
n
] или Х
n
, случайной
величины Х определяется как:
M[X
n
]=X
n
=
Первый начальный момент (n=1) случайной величины Х называется
математическим ожиданием или средним значением случайной величины и, согласно
(1.14), задается равенством:
M[X]=X=
Следует отметить, что начальный момент n-го порядка случайной величины - это
математическое ожидание ее n-ой степени.
Математическое ожидание суммы случайных величин равно сумме
математических ожиданий слагаемых, то есть
M[X
1
+X
2
+…+X
m
]=M[X
1
]+M[X
2
]+…+M[X
m
]
и здесь неважно, зависимы или независимы случайные величины X
1
, X
2
, ... , X
m.
В то же
время математическое ожидание произведения случайных величин равно произведению
математических ожиданий, то есть
M[X
1
X
2
…X
m
]=M[X
1
]M[X
2
]…M[X
m
]
только в том случае, когда случайные величины независимы.
Рассмотрим теперь непрерывную случайную величину Y, которая является
функцией другой случайной величины Х, то есть Y=g(X).
Тогда математическое ожидание случайной величины Y определяется через
плотность распределения ее аргумента X равенством:
M[Y]=M[g(X)]=
dxxfxg )()(
.
Этот результат известен как основная теорема о математических ожиданиях.
Центральный момент n-го порядка случайной величины Х определяетcя как:
M[(X-X)
n
]= (1.16)
Разность Х-Х между случайной величиной и математическим ожиданием
называется центрированной случайной величиной и характеризует отклонение случайной
величины от ее среднего значения. Очевидно, что центральный момент n-го порядка
случайной величины есть математическое ожидание n-ой степени соответствующей
центрированной случайной величины. Легко показать, что для случайной величины
центральный момент 1-го порядка или математическое ожидание центрированной
случайной величины всегда равно нулю:
M[(X-X)]=M[X]-M[X]=X-X=0.
i
m
i
n
i
Px
1
, если X – ДСВ;
dxxfx
n
)(
, если X – НСВ.
i
m
i
i
Px
1
- для ДСВ;
dxxfx )(
- для НСВ.
i
n
m
i
i
PXx )(
1
, если X – ДСВ;
dxxfXx
n
)()(
, если X – НСВ.
(1.14)
(1.15)
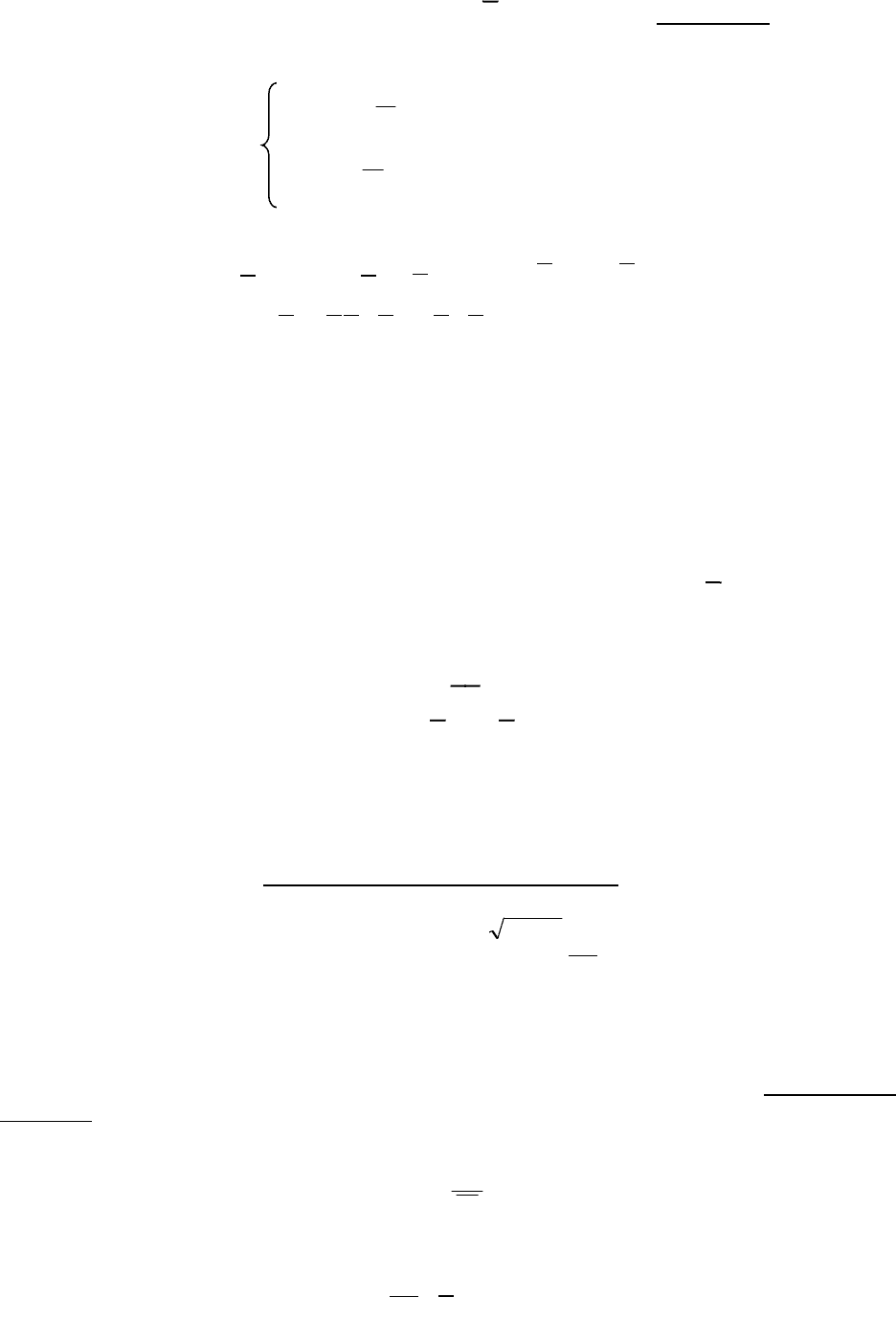
Второй центральный момент M[(X-X)
2
] называется дисперсией случайной
величины и обозначается через D[X] или D
x
. Для непосредственного вычисления
дисперсии, согласно (1.16), служат формулы:
D
x
=D[X]= (1.17)
Дисперсия может быть определена через математическое ожидание и второй
начальный момент:
D
x
=M[(X-X)
2
]=M[X
2
-2XX+(X)
2
]=M[X
2
]-2XM[X]+(X)
2
=
=X
2
-2XX+(X)
2
=X
2
-(X)
2
.
(1.18)
Дисперсия суммы независимых случайных величин Х
1
, Х
2
, ..., Х
m
равна сумме их
дисперсий, то есть:
D[X
1
+X
2
+…+X
m
]=D[X
1
]+D[X
2
]+…+D[X
m
].
Предположим теперь, что количество случайных величин в сумме тоже случайно,
то есть определим случайную величину
Y=
N
i
i
X
1
,
где N - случайная величина со средним значением N и дисперсией D
n
, а Х
1
, Х
2
,..., Х
n
-
одинаково распределенные независимые случайные величины. В этом случае
математическое ожидание и дисперсия случайной величины Y определяются равенствами:
Y=NX;
D
y
=ND
x
+(X)
2
D
n
.
Дисперсия случайной величины характеризует рассеивание, то есть разброс
случайной величины относительно ее математического ожидания, и имеет размерность
квадрата случайной величины. Однако удобнее пользоваться характеристикой
рассеивания, размерность которой совпадает с размерностью случайной величины. Такой
характеристикой является среднее квадратическое отклонение, обозначаемое как
[X] или
x
и определяемое как квадратный корень из дисперсии:
[X]=
x
=
][XD
Таким образом, математическое ожидание X и дисперсия D
x
(или среднее
квадратическое отклонение
x
) характеризуют наиболее важные особенности
распределения: его положение и степень разбросанности.
В некоторых случаях в качестве безразмерной характеристики разброса значений
случайной величины относительно математического ожидания используют коэффициент
вариации, который определяется как отношение среднего квадратического отклонения к
среднему значению:
x
=
X
x
.
Используя выражения (1.18) - (1.20), можно получить соотношение, связывающее
второй начальный момент случайной величины с коэффициентом вариации:
X
2
=X
2
(1+
2
x
)
В таблице приведены основные числовые характеристики (математическое
ожидание, второй начальный момент, дисперсия, среднее квадратическое отклонение,
i
m
i
i
PXx
2
1
)(
- для ДСВ;
dxxfXx )()(
2
- для НСВ.
(1.19)
(1.20)
(1.21)
