Лекции - Математическая логика
Подождите немного. Документ загружается.


101
äîêàçàòü ïîñòðîåíèåì ñîîòâåòñòâóþùåãî äåðåâà N
k
-âûâîäà. Çàìå-
òèì, ÷òî ìîæíî áûëî íå ïðèáåãàòü ê äîêàçàííûì âûøå óòâåðæäå-
íèÿì, à íåïîñðåäñòâåííî ñëåäóÿ îïðåäåëåíèþ, äîêàçàòü, ÷òî äëÿ
ëþáûõ Ã, À è Ñ
kk
k
NN
N
Ã, è Ã,
Ã
AC AC
C
¬
 çàâèñèìîñòè îò òîãî, ÿâëÿåòñÿ ñõåìà çàêëþ÷åíèé ïðÿìîé èëè
êîñâåííîé, ïðîèçâîäíîå N-ïðàâèëî òàêæå áóäåì íàçûâàòü ïðÿìûì
èëè êîñâåííûì.
Çàìå÷àíèå 1. Î÷åâèäíî, âñÿêîå ïðîèçâîäíîå N
i
-ïðàâèëî ÿâëÿ-
åòñÿ ïðîèçâîäíûì N
k
-ïðàâèëîì. Îáðàòíîå íåâåðíî, ÷òî áóäåò äî-
êàçàíî ïîçæå.
S Ïîñòðîåíèåì ñîîòâåòñòâóþùèõ äåðåâüåâ N
c
-âûâîäà ìîæíî äî-
êàçàòü, ÷òî ñëåäóþùèå ñõåìû ÿâëÿþòñÿ ïðîèçâîäíûìè N
c
-ïðàâè-
ëàìè:
1)
()
()
⊃⊃
⊃⊃
ABC
BAC
– ïðàâèëî ïåðåñòàíîâêè ïîñûëîê;
2)
()
&
⊃⊃
⊃
ABC
ABC
– ïðàâèëî ñîåäèíåíèÿ ïîñûëîê;
3)
&
()
⊃
⊃⊃
ABC
ABC
– ïðàâèëî ðàçúåäèíåíèÿ ïîñûëîê;
4)
⊃
¬⊃¬
AB
BA
– ïðàâèëî êîíòðàïîçèöèè;
5)
⊃⊃
⊃
ABBC
AC
– ïðàâèëî ñèëëîãèçìà;
6)
∨¬ABB
A
– ïðàâèëî äîêàçàòåëüñòâà èñêëþ÷åíèåì ñëó÷àåâ;
7)
¬¬
A
A
– ïðàâèëî ââåäåíèÿ äâîéíîãî îòðèöàíèÿ;
8)
()
&
¬∨
¬¬
AB
AB
,
&
()
¬¬
¬∨
AB
AB
,
(&)
¬∨¬
¬
AB
AB
– ïðàâèëà äå Ìîðãàíà â N
i
è N
k
;
9)
(&)
¬
¬∨¬
AB
AB
– ïðàâèëî äå Ìîðãàíà (N
k
-ïðàâèëî);
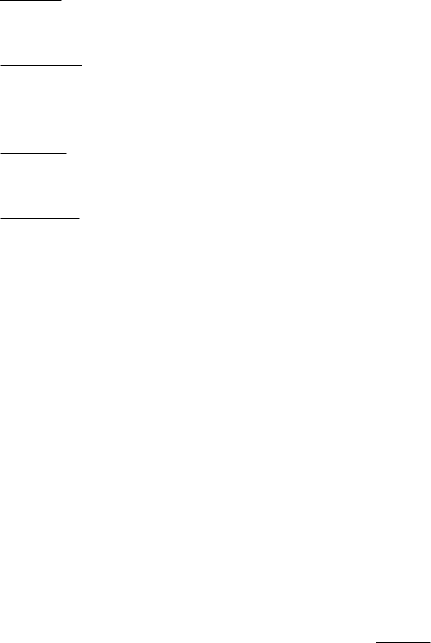
102
10)
⊃
¬∨
AB
AB
– ïðàâèëî âûðàæåíèÿ ⊃ ÷åðåç ∨ è ¬ (N
k
-ïðàâèëî);
11)
¬⊃¬
⊃
AB
BA
– ïðàâèëî îáðàòíîé êîíòðàïîçèöèè
(N
k
-ïðàâèëî);
12)
∨
¬⊃
AB
AB
– ïðàâèëî âûðàæåíèÿ ∨ ÷åðåç ⊃ è ¬;
13)
()
&
¬⊃
¬
AB
AB
– ïðàâèëî ïðåîáðàçîâàíèÿ
îòðèöàíèÿ èìïëèêàöèè.
Çàìå÷àíèå 2. Ñõåìû 9–11 ÿâëÿþòñÿ ïðîèçâîäíûìè N
k
-ïðàâè-
ëàìè, îäíàêî ìîæíî äîêàçàòü, ÷òî îíè íå ÿâëÿþòñÿ ïðîèçâîäíûìè
N
i
-ïðàâèëàìè. Âñå îñòàëüíûå ñõåìû ÿâëÿþòñÿ ïðîèçâîäíûìè êàê
äëÿ N
k
, òàê è äëÿ N
i
.
Òåïåðü îñòàíîâèìñÿ íà âîïðîñå, êàê ïî ïðîèçâîëüíîé ñõåìå
çàêëþ÷åíèé âûÿñíèòü, ÿâëÿåòñÿ ëè îíà ïðîèçâîäíûì N
i
- èëè
N
k
-ïðàâèëîì? Äëÿ ñèñòåìû N
k
ýòà ïðîáëåìà ðåøàåòñÿ ëåãêî.
ÒÅÎÐÅÌÀ. Ñõåìà çàêëþ÷åíèé ÿâëÿåòñÿ ïðîèçâîäíûì N
k
-ïðàâè-
ëîì òîãäà è òîëüêî òîãäà, êîãäà îíà ñîõðàíÿåò îòíîøåíèå ñåìàíòè-
÷åñêîãî ñëåäîâàíèÿ
.
Äîêàçàòåëüñòâî. Ïîñêîëüêó ïðàâèëà ⊃â è ⊃ó ñîõðàíÿþò
îòíîøåíèå
, òî, ñîãëàñíî êðèòåðèþ ñîõðàíåíèÿ îòíîøåíèÿ ρ,
ñëó÷àé êîñâåííîãî ïðàâèëà ñâîäèòñÿ ê ñëó÷àþ ïðÿìîãî ïðàâèëà.
Èòàê, ðàññìîòðèì ïðîèçâîëüíóþ ïðÿìóþ ñõåìó
...
n
FF
F
1
. Â ñèëó ñî-
ãëàñîâàííîñòè îòíîøåíèé N
k
-âûâîäèìîñòè è ñåìàíòè÷åñêîãî ñëå-
äîâàíèÿ, äëÿ ëþáûõ ôîðìóë F
1
, ..., F
n
, F
F
1
, ..., F
n
k
N
F ↔ F
1
, ..., F
n
F.
Òåïåðü îñòàëîñü òîëüêî åùå ðàç ïðèìåíèòü êðèòåðèé ñîõðàíåíèÿ
îòíîøåíèÿ ρ (§ 2.6), ðàññìîòðåâ â êà÷åñòâå ρ îòíîøåíèÿ
k
N
è
.
Çàìå÷àíèå 3. Ïîçæå áóäåò äîêàçàíî, ÷òî àíàëîãè÷íîå óòâåðæäå-
íèå äëÿ N
i
-ïðîèçâîäíûõ ïðàâèë íå èìååò ìåñòà, îäíàêî âåðíî ñëåäó-
þùåå: âñÿêîå N
i
-ïðîèçâîäíîå ïðàâèëî ñîõðàíÿåò îòíîøåíèå
.

103
Ïîëüçóÿñü òîëüêî ÷òî äîêàçàííîé òåîðåìîé è ïîñëåäóþùèì
çàìå÷àíèåì, ìîæíî äîêàçàòü, íàïðèìåð, ÷òî ñëåäóþùèå ñõåìû íå
ÿâëÿþòñÿ íè N
i
-, íè N
k
-ïðîèçâîäíûìè:
⊃
¬⊃¬
AB
AB
;
&
&
()¬
¬¬
AB
AB
;
()
¬∨¬
¬∨
AB
AB
.
Ñèñòåìû åñòåñòâåííîãî âûâîäà N
1
è N
2
íàçûâà-
þò ðàâíîîáúåìíûìè ñèñòåìàìè è ïèøóò N
1
f N
2
,
åñëè êëàññû âûâîäèìûõ â íèõ ôîðìóë ñîâïàäà-
þò, ò. å. åñëè
(F) (
1
N
F ↔
2
N
F).
Î÷åâèäíî, äëÿ ëþáûõ ñèñòåì N
1
è N
2
, åñëè îòíîøåíèÿ N
1
-
âûâîäèìîñòè è N
2
-âûâîäèìîñòè ñîãëàñîâàíû äðóã ñ äðóãîì, ò. å.
åñëè
(Ã) (F) (Ã
1
N
F ↔ Ã
2
N
F),
òî ñèñòåìû N
1
è N
2
ðàâíîîáúåìíû.
! ÒÅÎÐÅÌÀ (êðèòåðèé ðàâíîîáúåìíîñòè ñèñòåì åñòåñòâåííîãî
âûâîäà). Ïóñòü N
1
è N
2
– ñèñòåìû, ñðåäè ïðàâèë êîòîðûõ åñòü ïðà-
âèëà ⊃ó è ⊃â. Ñèñòåìû N
1
è N
2
ðàâíîîáúåìíû òîãäà è òîëüêî òîã-
äà, êîãäà âñÿêîå N
1
-ïðàâèëî ÿâëÿåòñÿ ïðîèçâîäíûì N
2
-ïðàâèëîì
è íàîáîðîò.
Äîêàçàòåëüñòâî. Äîêàæåì, ÷òî ñëåäóþùèå òðè óñëîâèÿ
ýêâèâàëåíòíû:
1) (F) (
1
N
F ↔
2
N
F) (ò. å. ñèñòåìû N
1
è N
2
ðàâíîîáúåìíû);
2) (Ã) (F) (Ã
1
N
F ↔ Ã
2
N
F) (ò. å. îòíîøåíèÿ
1
N
è
2
N
ñîãëàñî-
âàíû äðóã ñ äðóãîì);
3) âñÿêîå N
1
-ïðàâèëî ÿâëÿåòñÿ ïðîèçâîäíûì N
2
-ïðàâèëîì è
íàîáîðîò.
Ñíà÷àëà äîêàæåì öåïî÷êó 3 → 2 → 1.
Ïóñòü âñÿêîå N
1
-ïðàâèëî ÿâëÿåòñÿ ïðîèçâîäíûì N
2
-ïðàâèëîì
è íàîáîðîò. Ïîñêîëüêó îòíîøåíèå
2
N
ðåôëåêñèâíî è ìîíîòîííî,
à âñÿêîå N
1
-ïðàâèëî ÿâëÿåòñÿ ïðîèçâîäíûì N
2
-ïðàâèëîì, ò. å. ñî-
õðàíÿåò îòíîøåíèå
2
N
, òî â ñèëó ïðèíöèïà èíäóêöèè äëÿ
Равнообъемные
системы

104
N
1
-âûâîäîâ (âî âòîðîé ôîðìå),
1
N
ñîãëàñîâàíî ñ
2
N
. Àíàëîãè÷-
íî ìîæíî äîêàçàòü, ÷òî
2
N
ñîãëàñîâàíî ñ
1
N
. Òàêèì îáðàçîì,
3 → 2. Èç óñëîâèÿ 2 ïðè ïóñòîì ìíîæåñòâå à ïîëó÷àåì 1. Òàêèì
îáðàçîì, 2 → 1.
Òåïåðü äîêàæåì öåïî÷êó 1 → 2 → 3.
Ñíà÷àëà äîêàæåì, ÷òî åñëè N
1
è N
2
– ñèñòåìû, ñðåäè ïðàâèë
êîòîðûõ åñòü ïðàâèëà ⊃ó è ⊃â, òî 1 → 2.
Ïóñòü ñèñòåìû N
1
è N
2
ðàâíîîáúåìíû. Äîêàæåì, ÷òî îòíîøå-
íèÿ
1
N
è
2
N
ñîãëàñîâàíû äðóã ñ äðóãîì. Ïóñòü Ã è F – ïðîèçâîëü-
íûå. Ñëó÷àé, êîãäà à = ∅, òðèâèàëåí. Åñëè à = {F
1
, ..., F
n
}, òî,
èñïîëüçóÿ ïðàâèëà ⊃ó è ⊃â, ïîëó÷àåì:
Ã
1
N
F ↔
1
N
F
1
⊃ (F
2
⊃ (… (F
n
⊃ F) ...)),
Ã
2
N
F ↔
2
N
F
1
⊃ (F
2
⊃ (… (F
n
⊃ F) ...)).
Ïîñêîëüêó N
1
è N
2
ðàâíîîáúåìíû, óñëîâèÿ, ñòîÿùèå ñïðàâà,
ýêâèâàëåíòíû, à çíà÷èò, ýêâèâàëåíòíû è óñëîâèÿ, ñòîÿùèå ñëåâà:
Ã
1
N
F ↔ Ã
2
N
F. Ñëåäîâàòåëüíî, îòíîøåíèÿ
1
N
è
2
N
ñîãëàñîâà-
íû äðóã ñ äðóãîì. Òàêèì îáðàçîì, äîêàçàíî, ÷òî 1 → 2.
Äîêàæåì òåïåðü, ÷òî 2 → 3. Ïóñòü îòíîøåíèÿ
1
N
è
2
N
ñîãëà-
ñîâàíû äðóã ñ äðóãîì. Äîêàæåì, ÷òî òîãäà âåðíî óòâåðæäåíèå ï. 3.
 ñèëó êðèòåðèÿ ïðîèçâîäíîñòè êîñâåííîãî ïðàâèëà äîñòàòî÷íî
îãðàíè÷èòüñÿ ïðÿìûìè ïðàâèëàìè. Ïóñòü R – ïðÿìàÿ ñõåìà
...
n
FF
F
1
.
 ñèëó ñîãëàñîâàííîñòè îòíîøåíèé
1
N
è
2
N
, äëÿ ëþáûõ ôîðìóë
F
1
, …, F
n
, F
F
1
, …, F
n
1
N
F ↔ F
1
, …, F
n
2
N
F.
Îòñþäà, â ñèëó êðèòåðèÿ ïðîèçâîäíîñòè ïðàâèëà, ïîëó÷àåì,
÷òî ñõåìà çàêëþ÷åíèé R ÿâëÿåòñÿ ïðîèçâîäíûì N
1
-ïðàâèëîì òîã-
äà è òîëüêî òîãäà, êîãäà R ÿâëÿåòñÿ ïðîèçâîäíûì N
2
-ïðàâèëîì.
Ñëåäîâàòåëüíî, âåðíî óòâåðæäåíèå ï. 3, à çíà÷èò, äîêàçàíî, ÷òî
2 → 3.
Çàìå÷àíèå 4. Íàëè÷èå ïðàâèë ⊃ó è ⊃â ñðåäè èñõîäíûõ ïðàâèë
ñèñòåì èñïîëüçîâàëîñü òîëüêî â äîêàçàòåëüñòâå öåïî÷êè 1 → 2 → 3.

105
S Òàêèì îáðàçîì, èìååì ñëåäóþùåå âàæíîå óòâåðæäåíèå, ïðåäîñ-
òàâëÿþùåå äîñòàòî÷íîå óñëîâèå ðàâíîîáúåìíîñòè äâóõ ñèñòåì: äëÿ
ëþáûõ ñèñòåì N
1
è N
2
, åñëè âñÿêîå N
1
-ïðàâèëî ÿâëÿåòñÿ ïðîèçâîä-
íûì N
2
-ïðàâèëîì è íàîáîðîò, òî ñèñòåìû N
1
è N
2
ðàâíîîáúåìíû.
Ïóñòü R – ïðîèçâîëüíàÿ ñõåìà çàêëþ÷åíèé. Îáîçíà÷èì ÷åðåç
N + R ñèñòåìó, êîòîðàÿ ïîëó÷àåòñÿ äîáàâëåíèåì ñõåìû R ê ïðàâè-
ëàì ñèñòåìû N â êà÷åñòâå îñíîâíîãî ïðàâèëà.
ÑËÅÄÑÒÂÈÅ 1. Äëÿ ëþáîé ñèñòåìû N, åñëè ñõåìà R – ïðîèç-
âîäíîå N-ïðàâèëî, òî ñèñòåìû N è N + R ðàâíîîáúåìíû.
! ÑËÅÄÑÒÂÈÅ 2 (õàðàêòåðèñòè÷åñêîå ñâîéñòâî ïðîèçâîäíîãî ïðà-
âèëà). Ïóñòü N – ñèñòåìà, ñðåäè ïðàâèë êîòîðîé åñòü ïðàâèëà ⊃ó è
⊃â. Ñõåìà R ÿâëÿåòñÿ ïðîèçâîäíûì N-ïðàâèëîì òîãäà è òîëüêî
òîãäà, êîãäà ñèñòåìà N ðàâíîîáúåìíà ñèñòåìå N + R.
Ñõåìó R íàçûâàþò äîïóñòèìûì N-ïðàâèëîì (èëè N-äîïóñòè-
ìîé), åñëè ñèñòåìà N ðàâíîîáúåìíà ñèñòåìå N + R (N f N + R).
Òàêèì îáðàçîì, ñîãëàñíî ñëåäñòâèþ 1, âñÿêîå ïðîèçâîäíîå
N-ïðàâèëî ÿâëÿåòñÿ N-äîïóñòèìûì, à ñîãëàñíî ñëåäñòâèþ 2, åñëè
N – ñèñòåìà, ñðåäè ïðàâèë êîòîðîé åñòü ïðàâèëà ⊃ó è ⊃â, ñõåìà R
ÿâëÿåòñÿ ïðîèçâîäíûì N-ïðàâèëîì òîãäà è òîëüêî òîãäà, êîãäà
îíà ÿâëÿåòñÿ äîïóñòèìûì N-ïðàâèëîì
1)
.
! ÒÅÎÐÅÌÀ. Ñèñòåìà N
k
ðàâíîîáúåìíà ñèñòåìå
*
k
N
, êîòîðàÿ
ïîëó÷àåòñÿ èç N
k
óäàëåíèåì ïðàâèëà ¬ó.
Äîêàçàòåëüñòâî. Ïîñêîëüêó N
k
=
*
k
N
+ (¬ó), â ñèëó ñëåä-
ñòâèÿ 1 èç êðèòåðèÿ ðàâíîîáúåìíîñòè ñèñòåì, äîñòàòî÷íî äîêà-
çàòü, ÷òî ïðàâèëî ¬ó ÿâëÿåòñÿ ïðîèçâîäíûì ïðàâèëîì ñèñòåìû
*
k
N
.
Äîêàæåì, ÷òî À, ¬À
*
k
N
 äëÿ ëþáûõ ôîðìóë À è Â. Äåéñòâèòåëü-
íî, äåðåâî ôîðìóë
в
y
AA
B
B
¬
¬¬
¬
¬¬
1)
Èíàÿ ñèòóàöèÿ â èñ÷èñëåíèÿõ ãèëüáåðòîâñêîãî òèïà (ñì. § 2.13): â èíòó-
èöèîíèñòñêîì èñ÷èñëåíèè òàêîãî òèïà ñóùåñòâóþò äîïóñòèìûå, íî íå ïðîèç-
âîäíûå ïðàâèëà, à â êëàññè÷åñêîì – âñÿêîå äîïóñòèìîå ïðàâèëî ÿâëÿåòñÿ ïðî-
èçâîäíûì.

106
ÿâëÿåòñÿ äåðåâîì
*
k
N
-âûâîäà ñ êîðíåì Â è ìíîæåñòâîì çåëåíûõ
ëèñòüåâ {À, ¬À}.
S Çàìå÷àíèå 5. Òàêèì îáðàçîì, èçíà÷àëüíî êëàññè÷åñêóþ ñèñòå-
ìó åñòåñòâåííîãî âûâîäà ìîæíî áûëî ñòðîèòü èç N
i
çàìåíîé ïðà-
âèëà ¬ó íà ïðàâèëî ¬¬ó.
★ Ñðåäè ïðàâèë ñèñòåì åñòåñòâåííîãî âûâîäà
N
i
è N
k
òðè êîñâåííûõ ïðàâèëà: ⊃â, ∨ó è ¬â.
Îêàçûâàåòñÿ, êàæäîå èç êîñâåííûõ N
c
-ïðà-
âèë ¬â è ∨ó ìîæíî çàìåíèòü ñîîòâåòñòâóþùèì
åìó ïðÿìûì ïðàâèëîì òàêèì îáðàçîì, ÷òî êëàñ-
ñû âûâîäèìûõ ôîðìóë ïðè ýòîì íå èçìåíÿòñÿ.
Ìîæíî ñ÷èòàòü, ÷òî êàæäîå èç êîñâåííûõ ïðàâèë ∨ó è ¬â â óêàçàí-
íîì ñìûñëå ýêâèâàëåíòíî ñîîòâåòñòâóþùåìó ïðÿìîìó ïðàâèëó.
Ðàññìîòðèì ñíà÷àëà ïðàâèëî ∨ó. Èìååò ìåñòî ñëåäóþùåå óò-
âåðæäåíèå.
ÓÒÂÅÐÆÄÅÍÈÅ 1. Ñèñòåìà N
c
ðàâíîîáúåìíà ñèñòåìå
c
N
′
, êî-
òîðàÿ ïîëó÷àåòñÿ èç N
c
çàìåíîé êîñâåííîãî ïðàâèëà ∨ó ïðÿìûì ïðà-
âèëîì (∨ó)
ï
∨⊃⊃ABA CBC
C
(Êîñâåííîå ïðàâèëî ∨ó ýêâèâàëåíòíî ïðÿìîìó ïðàâèëó (∨ó)
ï
.)
Äîêàçàòåëüñòâî. Èç êðèòåðèÿ ïðîèçâîäíîñòè ïðàâèëà
ñëåäóåò, ÷òî:
à) ñõåìà (∨ó)
ï
ÿâëÿåòñÿ ïðîèçâîäíûì N
c
-ïðàâèëîì;
á) ïðàâèëî ∨ó ÿâëÿåòñÿ ïðîèçâîäíûì â ñèñòåìå
c
N
′
.
Îòñþäà, ñîãëàñíî êðèòåðèþ ðàâíîîáúåìíîñòè ñèñòåì, ïîëó÷à-
åì, ÷òî ñèñòåìû N
c
è
c
N
′
ðàâíîîáúåìíû.
Àíàëîãè÷íî ìîæíî äîêàçàòü ñëåäóþùåå óòâåðæäåíèå.
ÓÒÂÅÐÆÄÅÍÈÅ 2. Ñèñòåìà N
c
ðàâíîîáúåìíà ñèñòåìå, êîòî-
ðàÿ ïîëó÷àåòñÿ èç N
c
çàìåíîé êîñâåííîãî ïðàâèëà ¬â ïðÿìûì ïðà-
âèëîì (¬â)
ï
⊃⊃¬
¬
ABA B
A
(Êîñâåííîå ïðàâèëî ¬â ýêâèâàëåíòíî ïðÿìîìó ïðàâèëó (¬â)
ï
.)
Дополнительные
замечания,
относящиеся
к косвенным
правилам

107
Çàìåòèì, ÷òî ïðè äîêàçàòåëüñòâå óòâåðæäåíèé 1 è 2 èñïîëüçó-
åòñÿ êîñâåííîå ïðàâèëî ⊃â. Èìåííî ýòî ïðàâèëî èãðàåò ñàìóþ ñó-
ùåñòâåííóþ ðîëü â ðåàëèçàöèè èäåè åñòåñòâåííîãî âûâîäà. Â óêà-
çàííîì ñìûñëå äîñòàòî÷íî èìåòü åäèíñòâåííîå êîñâåííîå ïðàâè-
ëî ⊃â.
Ìîæíî äîêàçàòü, ÷òî ñèñòåìà N
k
ðàâíîîáúåìíà ñèñòåìå, êîòî-
ðàÿ ïîëó÷àåòñÿ èç N
k
çàìåíîé ïðàâèëà ¬â íà äâà ïðàâèëà: ïðàâèëî
êîíòðàïîçèöèè
⊃
¬⊃¬
AB
BA
è ïðàâèëî ââåäåíèÿ äâîéíîãî îòðèöàíèÿ
¬¬
A
A
. ✰
§ 2.9. Äåäóêòèâíàÿ ïîëíîòৠ2.9. Äåäóêòèâíàÿ ïîëíîòà
§ 2.9. Äåäóêòèâíàÿ ïîëíîòৠ2.9. Äåäóêòèâíàÿ ïîëíîòà
§ 2.9. Äåäóêòèâíàÿ ïîëíîòà
Íàïîìíèì, ÷òî ÷åðåç N + R ìû îáîçíà÷àåì
ñèñòåìó, êîòîðàÿ ïîëó÷àåòñÿ èç ñèñòåìû N äîáàâëåíèåì ê åå
ïðàâèëàì ñõåìû R â êà÷åñòâå îñíîâíîãî ïðàâèëà. Óæå óñòàíîâ-
ëåíî, ÷òî ïðè äîáàâëåíèè ïðîèçâîäíîãî N-ïðàâèëà ê èñõîä-
íûì N-ïðàâèëàì êëàññ âûâîäèìûõ ôîðìóë íå ðàñøèðÿåòñÿ:
N + R
~
N. Åñëè ñõåìà R íå ÿâëÿåòñÿ ïðîèçâîäíûì N-ïðàâè-
ëîì, òî êëàññ (N + R)-âûâîäèìûõ ôîðìóë ÿâëÿåòñÿ áîëåå øè-
ðîêèì, ÷åì êëàññ N-âûâîäèìûõ ôîðìóë (ñèñòåìà N + R ÿâëÿ-
åòñÿ ñîáñòâåííûì ðàñøèðåíèåì ñèñòåìû N). Ïðè ýòîì ñèñòåìà
N + R ìîæåò ïîëó÷èòüñÿ ïðîòèâîðå÷èâîé. Êàêèå ñèñòåìû ìîæ-
íî òàêèì îáðàçîì ðàñøèðÿòü, ïîëó÷àÿ â ðåçóëüòàòå íåïðîòèâî-
ðå÷èâûå ñèñòåìû?
!
Ñèñòåìó åñòåñòâåííîãî âûâîäà N íàçûâàþò äåäóêòèâíî ïîëíîé
(ñèíòàêñè÷åñêè ïîëíîé), åñëè äëÿ ëþáîé ñõåìû çàêëþ÷åíèé R,
íå ÿâëÿþùåéñÿ ïðîèçâîäíûì N-ïðàâèëîì, ñèñòåìà N + R ïðî-
òèâîðå÷èâà.
Íàïðèìåð, ñèñòåìà N
i
íå ÿâëÿåòñÿ äåäóêòèâíî ïîëíîé. Äåé-
ñòâèòåëüíî, ïðàâèëî ñíÿòèÿ äâîéíîãî îòðèöàíèÿ ¬¬ó íå ÿâëÿåòñÿ
ïðîèçâîäíûì ïðàâèëîì N
i
(÷òî áóäåò äîêàçàíî ïîçæå), à ñèñòåìà
N
i
+ ¬¬ó ñîâïàäàåò ñ N
k
è, ñëåäîâàòåëüíî, íåïðîòèâîðå÷èâà.
! ÒÅÎÐÅÌÀ (î äåäóêòèâíîé ïîëíîòå N
k
). Ñèñòåìà N
k
äåäóêòèâíî
ïîëíà, ò. å. äëÿ ëþáîé ñõåìû çàêëþ÷åíèé R, íå ÿâëÿþùåéñÿ ïðî-
èçâîäíûì N
k
-ïðàâèëîì, ñèñòåìà N
k
+ R ïðîòèâîðå÷èâà.
108
Äîêàçàòåëüñòâî. Ïóñòü ñõåìà R íå ÿâëÿåòñÿ ïðîèçâîä-
íûì N
k
-ïðàâèëîì. Äîêàæåì, ÷òî ñèñòåìà N
k
+ R ïðîòèâîðå-
÷èâà.
 ñèëó õàðàêòåðèñòè÷åñêîãî ñâîéñòâà ïðîèçâîäíîãî ïðàâèëà, êëàññ
(N
k
+ R)-âûâîäèìûõ ôîðìóë øèðå, ÷åì êëàññ N
k
-âûâîäèìûõ ôîðìóë.
Ïóñòü G – òàêàÿ ôîðìóëà, ÷òî
k
N
R
+
G, íî
k
N
/
G. Ïîñêîëüêó
k
N
/
G, òî
/
G â ñèëó òåîðåìû î ñåìàíòè÷åñêîé ïîëíîòå N
k
. Ïóñòü ω = (
1
i
p
, …,
m
i
p
) –
ñîáñòâåííûé ñïèñîê ïåðåìåííûõ ôîðìóëû G, à α = (α
1
, …, α
m
) – ïðî-
èçâîëüíûé íàáîð òîé æå äëèíû, òàêîé ÷òî
||
G
ω
α
= Ë.
Ðàññìîòðèì òàêóþ ïîäñòàíîâêó S â ôîðìóëó G, ïðè êîòîðîé
âìåñòî êàæäîé ïåðåìåííîé
k
i
p
èç ω ïîäñòàâëÿåòñÿ ôîðìóëà
11
()
k
pp
α
⊃
(ãäå k = 1, …, m). Ïîëó÷åííóþ â ðåçóëüòàòå òàêîé ïîä-
ñòàíîâêè ôîðìóëó îáîçíà÷èì ÷åðåç G*. Çàìåòèì, ÷òî ôîðìóëà G*
èìååò åäèíñòâåííóþ ïåðåìåííóþ p
1
.
Äîêàæåì, ÷òî ôîðìóëà ¬G* ÿâëÿåòñÿ òàâòîëîãèåé. Äåéñòâèòåëü-
íî, êàêîå áû èñòèííîñòíîå çíà÷åíèå β
1
ìû íè ïðèäàëè ïåðåìåí-
íîé p
1
, ïîëó÷èì
1
1
11
|
()
|
k
p
pp
α
β
⊃
= α
k
(k = 1, …, m). Îòñþäà ñëåäóåò,
÷òî
1
1
*
||||
p
GG
ω
β
α
=
= Ë äëÿ ëþáîãî β
1
èç ìíîæåñòâà {È, Ë} (ñì. óò-
âåðæäåíèå î çíà÷åíèè ðåçóëüòàòà ïîäñòàíîâêè èç § 1.3). Ýòî êàê
ðàç è îçíà÷àåò, ÷òî
¬G*. Îòñþäà ïî òåîðåìå î ñåìàíòè÷åñêîé
ïîëíîòå N
k
ïîëó÷àåì, ÷òî ôîðìóëà ¬G* âûâîäèìà â N
k
, à çíà÷èò,
îíà âûâîäèìà è â N
k
+ R:
K
N
R
+
¬G*.
Âìåñòå ñ òåì, ïîñêîëüêó G âûâîäèìà â ñèñòåìå N
k
+ R, òî è
ôîðìóëà G*, êàê ðåçóëüòàò ïîäñòàíîâêè â íåå, òàêæå âûâîäèìà â
N
k
+ R:
K
N
R
+
G*. Èòàê, èìååì îäíîâðåìåííî:
K
N
R
+
G* è
K
N
R
+
¬G*.
Òàêèì îáðàçîì, äîêàçàíî, ÷òî ñèñòåìà N
k
+ R ïðîòèâîðå÷èâà.
ÑËÅÄÑÒÂÈÅ. Ñèñòåìà N
k
+ R ïðîòèâîðå÷èâà òîãäà è òîëüêî
òîãäà, êîãäà ñõåìà çàêëþ÷åíèé R íå ÿâëÿåòñÿ ïðîèçâîäíûì
N
k
-ïðàâèëîì.
Äîêàçàòåëüñòâî. Åñëè ñõåìà R ÿâëÿåòñÿ ïðîèçâîäíûì
N
k
-ïðàâèëîì, òî, ñîãëàñíî õàðàêòåðèñòè÷åñêîìó ñâîéñòâó ïðîèç-
âîäíîãî ïðàâèëà, ñèñòåìà N
k
+ R ðàâíîîáúåìíà N
k
, à çíà÷èò, íå-
ïðîòèâîðå÷èâà.
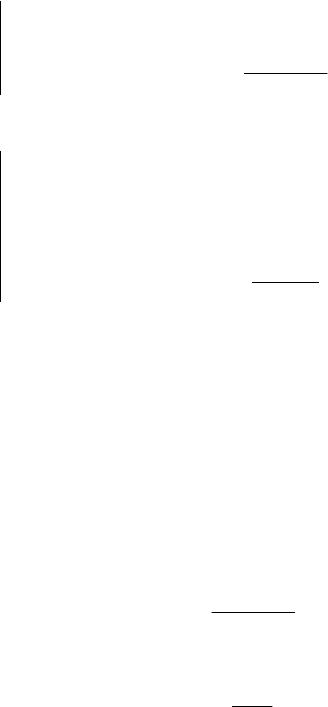
109
Åñëè ñõåìà R íå ÿâëÿåòñÿ ïðîèçâîäíûì N
k
-ïðàâèëîì, òî, ñî-
ãëàñíî òåîðåìå î äåäóêòèâíîé ïîëíîòå N
k
, ñèñòåìà N
k
+ R ïðîòè-
âîðå÷èâà.
§ 2.10. Ñõåìû äîêàçàòåëüñòâৠ2.10. Ñõåìû äîêàçàòåëüñòâà
§ 2.10. Ñõåìû äîêàçàòåëüñòâৠ2.10. Ñõåìû äîêàçàòåëüñòâà
§ 2.10. Ñõåìû äîêàçàòåëüñòâà
îò ïðîòèâíîãî è ïðèâåäåíèåìîò ïðîòèâíîãî è ïðèâåäåíèåì
îò ïðîòèâíîãî è ïðèâåäåíèåìîò ïðîòèâíîãî è ïðèâåäåíèåì
îò ïðîòèâíîãî è ïðèâåäåíèåì
ê íåëåïîñòèê íåëåïîñòè
ê íåëåïîñòèê íåëåïîñòè
ê íåëåïîñòè
!
Ñõåìîé äîêàçàòåëüñòâà îò ïðîòèâíîãî íàçûâàþò ñõåìó
[][]¬¬
¬
AA
BB
A
Îíà ôîðìàëèçóåò ìåòîä äîêàçàòåëüñòâà îò ïðîòèâíîãî.
!
Ñõåìîé äîêàçàòåëüñòâà ïðèâåäåíèåì ê íåëåïîñòè íàçûâàþò
ñõåìó, õîðîøî èçâåñòíóþ íàì êàê ñõåìó ââåäåíèÿ îòðèöàíèÿ
(‰):
[] []
¬
¬
AA
BB
A
Îíà ôîðìàëèçóåò ìåòîä äîêàçàòåëüñòâà ïðèâåäåíèåì ê íåëå-
ïîñòè.
Ýòè ñõåìû ïîõîæè äðóã íà äðóãà, â ñâÿçè ñ ÷åì èõ ÷àñòî
ïóòàþò. Îäíàêî íåñìîòðÿ íà íåêîòîðîå ñõîäñòâî, îíè èìåþò
ðàçíóþ ôîðìó. Ïðè÷åì ðàçëè÷àþòñÿ îíè íå òîëüêî ïî ôîðìå,
íî è ïî ñóùåñòâó, è ðàçëè÷èå ýòî íîñèò ïðèíöèïèàëüíûé õàðàê-
òåð.
Óñòàíîâèì ñíà÷àëà âçàèìîñâÿçü ìåæäó îáñóæäàåìûìè ñõåìà-
ìè.
Ðàññìîòðèì òðè ñõåìû çàêëþ÷åíèé:
– ñõåìó äîêàçàòåëüñòâà îò ïðîòèâíîãî
[][]¬¬
¬
AA
BB
A
(I)
– ñõåìó ñíÿòèÿ äâîéíîãî îòðèöàíèÿ ¬¬ó
¬¬A
A
(II)
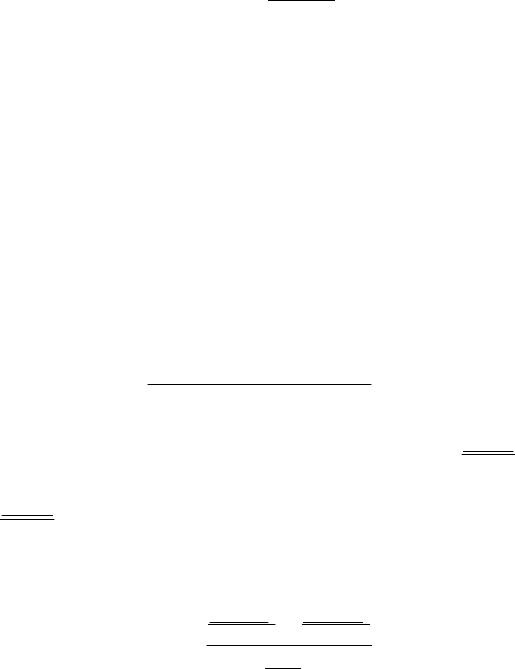
110
– ñõåìó äîêàçàòåëüñòâà ïðèâåäåíèåì ê íåëåïîñòè (¬â)
[] []
¬
¬
AA
BB
A
(III)
! ÒÅÎÐÅÌÀ. Ñõåìà äîêàçàòåëüñòâà îò ïðîòèâíîãî (I) ýêâèâàëåí-
òíà ñîâîêóïíîñòè äâóõ ñõåì – ñõåìû ñíÿòèÿ äâîéíîãî îòðèöàíèÿ
(II) è ñõåìû äîêàçàòåëüñòâà ïðèâåäåíèåì ê íåëåïîñòè (III) â ñëåäó-
þùåì ñìûñëå. Äëÿ ëþáîé ñèñòåìû åñòåñòâåííîãî âûâîäà:
1) åñëè ñõåìû (II) è (III) ÿâëÿþòñÿ îñíîâíûìè ïðàâèëàìè ñèñ-
òåìû, òî ñõåìà (I) ÿâëÿåòñÿ åå ïðîèçâîäíûì ïðàâèëîì;
2) åñëè ñõåìà (I) ÿâëÿåòñÿ îñíîâíûì ïðàâèëîì ñèñòåìû, òî ñõå-
ìû (II) è (III) ÿâëÿþòñÿ åå ïðîèçâîäíûìè ïðàâèëàìè.
Äîêàçàòåëüñòâî.
1. Ïóñòü N – ñèñòåìà, äëÿ êîòîðîé ñõåìû ¬¬ó (II) è ¬â (III)
ÿâëÿþòñÿ îñíîâíûìè ïðàâèëàìè. Äîêàæåì, ÷òî ñõåìà (I) ÿâëÿåòñÿ
ïðîèçâîäíûì N-ïðàâèëîì, ò. å. äëÿ ëþáûõ ôîðìóë À, Â è ëþáîãî
êîíå÷íîãî ìíîæåñòâà ôîðìóë Ã
NN
N
Ã, ; Ã,
Ã
AB A B
A
¬¬¬
.(IR)
Äîïóñòèì, ÷òî Ã, ¬À
N
 è Ã, ¬À
N
¬Â. Ïóñòü
1
A
B
Δ¬
(Δ
1
⊆ Ã) è
2
A
B
Δ¬
¬
(Δ
2
⊆ Ã) – íåêîòîðûå ñîîòâåòñòâóþùèå äåðåâüÿ N-âûâîäà.
Äîêàæåì, ÷òî Ã
N
À, ïîñòðîèâ ñîîòâåòñòâóþùåå äåðåâî N-âûâîäà:
12
11
III (1)
II
[] []
AA
BB
A
A
Δ¬ Δ¬
¬
¬¬
2. Ïóñòü N – ñèñòåìà, äëÿ êîòîðîé ñõåìà (I) ÿâëÿåòñÿ îñíîâ-
íîé. Äîêàæåì, ÷òî ñõåìû ¬¬ó (II) è ¬â (III) ÿâëÿþòñÿ ïðîèçâîäíûìè
N-ïðàâèëàìè.
Ñíà÷àëà äîêàæåì, ÷òî ïðàâèëî ¬¬ó ÿâëÿåòñÿ ïðîèçâîäíûì
N-ïðàâèëîì. Ïîñêîëüêó ýòî ïðÿìîå ïðàâèëî, äîñòàòî÷íî äîêàçàòü,
÷òî äëÿ ëþáîé ôîðìóëû À
¬¬À
N
À. (IIR)
