Лаврусь О.Е. (сост.), Лаврусь В.В. (сост.) Методические указания и варианты заданий к экзаменационному тесту (ряды, теория вероятностей, математическая статистика) для студентов заочной формы обучения

Подождите немного. Документ загружается.

Экзаменационные тесты (ряды, теория вероятностей, математическая статистика) Составитель: Лаврусь О.Е.

Лаврусь В.В.

ВАРИАНТ 15

1. Ряд чисел 2, 4, 8, 16… образует:

A) арифметическую прогрессию;

B) геометрическую прогрессию со знаменателем q = 2;

C) геометрическую прогрессию со знаменателем q = -2;

D) геометрическую прогрессию со знаменателем q = 4.

2. Четвертый член ряда

()

∑

∞

−⋅

−

равен:

A) 0,125;

B) 0,2;

C) –0,125;

D) –0,2.

3. Общий член ряда

125

+−

… равен:

()

∑

∞

⋅−

;

()

∑

∞

⋅−

;

()

∑

∞

⋅−

;

∑

∞

4. Сумма первых трех членов ряда

()( )

∑

∞

−⋅−

равна:

A) –

; B)

; C) –

; D)

5. Найти интервал сходимости функционального ряда

()

∑

∞

−

A) – 2 < x < 2;

B) – 4 < x < 4;

C) – 2 < x < 6;

D) – 6 < x < 2.

6. Вероятность появления хотя бы одного из двух совместных событий А и В равна:

A) Р(А + В) = Р(А)·Р(В);

B) Р(А + В) = Р(А) + Р(В) + Р(АВ);

C) Р(А + В) = Р(А) + Р(В);

D) Р(А + В) = Р(А) + Р(В) – Р(АВ).

7. Локальная формула Муавра-Лапласа имеет вид:

() ()

⋅=

;

() ()

npq

⋅=

;

() ()

npq

⋅=

;

() ()

npq

⋅=

8. В урне содержится 5 одинаковых шаров, причем 2 из них белого цвета, 2 – красного, 1 –

зеленого. Наудачу извлечены 3 шара. Найти вероятность того, что среди трех

извлеченных шаров окажется два белых шара и один красный.

A) 0,4;

B) 0,6;

C) 0,2;

D) 0,5.

9. Два равносильных противника играют в шахматы. Найти вероятность того, что

первый игрок выиграет три партии из четырех. (Ничьи в расчет не принимаются).

A) 1/2;

B) 3/8;

C) 1/4;

D) 5/16.

10. Вероятность наступления события A в каждом испытании равна 0,6. Вероятность

того, что в результате проведения 2000 независимых испытаний событие A наступит

ровно 1400 раз, вычисляется:

A) по формуле Бернулли;

B) по интегральной формуле Лапласа;

C) по локальной формуле Муавра-Лапласа;

D) по формуле Пуассона.

11. Дисперсия суммы постоянной величины C и случайной величины X равна:

A) D(C + X) = C + D(X);

B) D(C + X) = D(X);

C) D(C + X) = 1 + D(X);

D) D(C + X) = C

+ D(X).

12. Дискретная случайная величина X задана законом распределения:

2 6 x

0,2 0,4 0,4

Если известно, что ее математическое ожидание M(X) равно 6, то x

равно:

A) 4; C) 7;

B) 5; D) 8.

ВАРИАНТ 15

13. Найти математическое ожидание случайной величины Z = X – 2Y + 4, если известны

математические ожидания независимых случайных величин X и Y: M(X) = 3, M(Y) = 1.

A) 9;

B) 1;

C) 4;

D) 5.

14. Случайная величина X задана интегральной функцией:

()

⎪

⎩

⎪

⎨

⎧

≤<

≤

.3при1

;30при

0;при0

Найти вероятность того, что в результате испытания X примет значение, заключенное в

интервале (1, 2).

A) 2/9;

B) 4/9;

C) 1/3;

D) 5/9.

15. Дана дифференциальная функция случайной величины X:

()

⎪

⎩

⎪

⎨

⎧

≤<

≤

.2при0

;20при

;0при0

Найти вероятность того, что в результате испытания X примет значение, заключенное в

интервале (1, 2).

A) 1/8;

B) 3/8;

C) 5/8;

D) 7/8.

16. Случайная величина X задана интегральной функцией:

()

⎪

⎩

⎪

⎨

⎧

≤<−

≤

.при1

;4при2

4;при0

Коэффициент β равен:

A) 5;

B) 6;

C) 8;

D) 10.

17. Найти моду статистической выборки: 6, 4, 2, 2, 3, 4, 6, 4, 3.

A) 4;

B) 6;

C) 2;

D) 3.

18. Если основная гипотеза имеет вид H

: a = 3, то конкурирующей может быть

гипотеза:

A) Н

: a ≠ 4;

B) Н

: a ≠ 2;

C) Н

: a < 3;

D) Н

: a ≤ 3.

19. Точечная оценка математического ожидания случайной величины, распределенной

по нормальному закону, равна 20. Тогда его интервальная оценка может быть записана

в виде:

A) (19,5; 21,5);

B) (19; 22);

C) (18; 21);

D) (18,5; 21,5).

20. Из генеральной совокупности извлечена выборка объема n = 60, полигон

относительных частот которой имеет вид

6912

Тогда число вариант x

= 9 в выборке равно:

A) 9;

B) 6;

C) 12;

D) 4;

21. Выборочное уравнение парной регрессии имеет вид y = 2 – 2x. Тогда выборочный

коэффициент корреляции может быть равен:

A) – 0,85;

B) – 2;

C) 2;

D) 0.

Экзаменационные тесты (ряды, теория вероятностей, математическая статистика) Составитель: Лаврусь О.Е.

Лаврусь В.В.

ВАРИАНТ 16

1. Дан знакочередующийся ряд

()

∑

∞

⋅−

a . Тогда

0lim =

∞→

называется:

A) необходимым признаком сходимости;

B) признаком Лейбница;

C) признаком Даламбера;

D) признаком Коши.

2. Четвертый член ряда

()

∑

∞

−

равен:

A) 1/4;

B) – 1/4;

C) – 1/3;

D) 1/3.

3. Общий член ряда

−+−

+ … равен:

∑

∞

−

;

()

∑

∞

⋅−

;

()

∑

∞

⋅−

;

()

∑

∞

⋅−

4. Сумма первых трех членов ряда

()

∑

∞

−

равна:

; B) –

; C)

; D) –

5. Найти интервал сходимости функционального ряда

()

∑

∞

−

A) – 2 < x < 2;

B) – 3 < x < 3;

C) – 5 < x < 1;

1 < x < 5.

6. Вероятность совместного появления двух зависимых событий А и В равна:

A) Р(АВ) = Р(А)·Р(В/А);

B) Р(АВ) = Р(А)·Р(А/В);

C) Р(АВ) = Р(В)·Р(В/А);

D) Р(АВ) = Р(А) + Р(В/А).

7. Число сочетаний из n элементов по m находится по формуле:

()

−

= ;

()

mnn

−

= ;

()

mnm

−

= ;

()

−

= .

8. В квадрат помещен другой квадрат, сторона которого вдвое меньше. Найти

вероятность того, что точка, брошенная в большой квадрат (любое ее положение

равновозможно), не попадет в малый квадрат.

A) 1/2;

B) 1/4;

C) 1/8;

D) 3/4.

9. Вратарь отражает пенальти с вероятностью 0,5. Найти вероятность того, что вратарь

отразит 4 пенальти из 5.

A) 1/5;

B) 5/16;

C) 5/32;

D) 3/16.

10. Вероятность поражения мишени при одном выстреле равна 0,8. Вероятность того,

что в результате 100 выстрелов мишень будет поражена более 75 раз, вычисляется:

A) по формуле Бернулли;

B) по интегральной формуле Лапласа;

C) по локальной формуле Муавра-Лапласа;

D) по формуле Пуассона.

11. Плотность вероятности непрерывной случайной величины обладает свойством:

()

∫

+∞

∞−

= 0dxxf

;

()

∫

+∞

∞−

∞=dxxf

;

()

∫

+∞

∞−

=1dxxf

;

()

∫

+∞

5,0dxxf

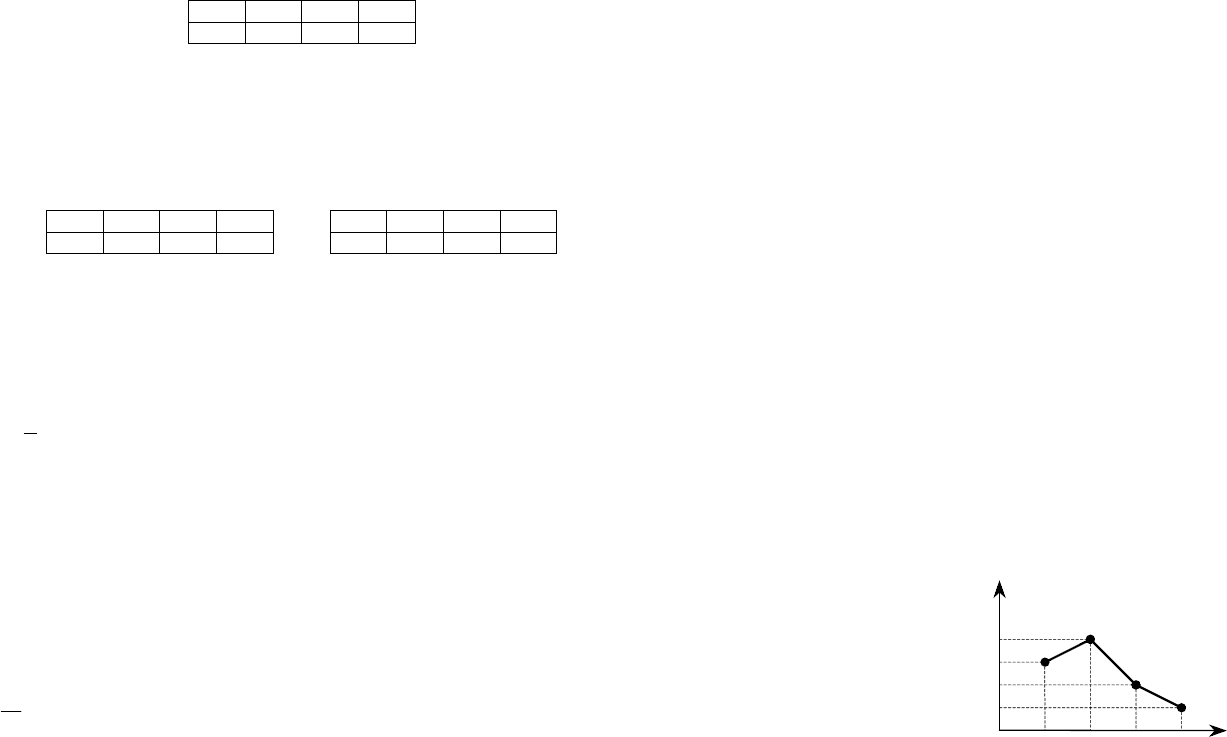
ВАРИАНТ 16

12. Дискретная случайная величина X задана законом распределения:

– 2 0 6

0,2 0,3

Математическое ожидание M(X) этой случайной величины равно:

A) 3;

B) 1;

C) 2,8;

D) 0,8.

13. Найти математическое ожидание случайной величины Z = X·Y, если известны

законы распределения независимых случайных величин X и Y:

3 6 0

5 8 0

0,4 0,5 0,1

0,2 0,5 0,3

A) 20;

B) 18;

C) 21;

D) 9,2.

14. Случайная величина X задана интегральной функцией:

()

⎪

⎩

⎪

⎨

⎧

≤<−+

−≤

.0при1

;05при

5;при0

Найти вероятность того, что в результате испытания X примет значение, заключенное в

интервале (– 4, – 1).

A) 4/5;

B) 2/5;

C) 1/5;

D) 3/5.

15. Дана дифференциальная функция случайной величины X:

()

⎪

⎩

⎪

⎨

⎧

≤<

≤

.3при0

;30при

;0при0

Найти вероятность того, что в результате испытания X примет значение, заключенное в

интервале (1, 2).

A) 1/9;

B) 19/27;

C) 7/27;

D) 1/27.

16. Дана дифференциальная функция случайной величины X:

()

⎪

⎩

⎪

⎨

⎧

≤<

≤

.1при0

;10при2

;0при0

Математическое ожидание X равно:

A) 2/3;

B) 1/3;

C) 1/2;

D) 5/6.

17. Найти моду статистической выборки

1, 7, 9, 4, 4, 7, 1, 9 ,4.

A) 9;

B) 7;

C) 4;

D) 1.

18.. Если основная гипотеза имеет вид H

: a =20 , то конкурирующей может быть

гипотеза:

A) Н

: a ≥ 10;

B) Н

: a <20;

C) Н

: a ≠ 10;

D) Н

: a ≤ 20.

19. Точечная оценка математического ожидания случайной величины, распределенной

по нормальному закону, равна 15,5. Тогда его интервальная оценка может быть

записана в виде:

A) (14; 16);

B) (14; 17);

C) (15; 17);

D) (13; 16).

20. Из генеральной совокупности извлечена выборка объема n = 30, полигон

относительных частот которой имеет вид

81216

Тогда число вариант x

= 8 в выборке равно:

A) 8;

B) 16;

C) 4;

D) 12;

21. Выборочное уравнение парной регрессии имеет вид y =– 2x – 8. Тогда выборочный

коэффициент корреляции может быть равен:

A) 0,125;

B) – 2;

C) 0;

D) – 0,7.

Экзаменационные тесты (ряды, теория вероятностей, математическая статистика) Составитель: Лаврусь О.Е.

Лаврусь В.В.

ВАРИАНТ 17

1. Признак Даламбера для знакоположительного числового ряда

∑

∞

a определяется

формулой:

∞→

lim

;

∞→

lim ;

→∞

lim ;

∞→

lim .

2. Второй член ряда

()

∑

∞

−⋅

равен:

A) 3/4;

B) – 3/4;

C) 2/3;

D) – 2/3.

3. Общий член ряда

+ … равен:

∑

∞

;

∑

∞

;

∑

∞

;

∑

∞

4. Сумма первых трех членов ряда

()

∑

∞

−

равна:

A) –

; B) –

; C)

; D) –

5. Найти интервал сходимости функционального ряда

()

∑

∞

−

A) – 3 < x < 3;

B) – 2 < x < 2;

C) – 5 < x < – 1;

1 < x < 5.

6. Два единственно возможных события, образующих полную группу, называются:

A) противоположными;

B) недостоверными;

C) совместными;

D) равновозможными.

7. Число размещений из n элементов по m находится по формуле:

()

mnm

−

= ;

()

−

= ;

()

−

= ;

= .

8. Среди 10 лотерейных билетов 2 выигрышных. Наудачу выбирают 2 билета. Найти

вероятность того, что оба билета окажутся невыигрышными.

A) 1/45;

B) 28/45;

C) 1/5;

D) 16/45.

9. Вероятность появления события А в одном испытании равна 0,6. Найти вероятность

того, что в трех независимых испытаниях событие А появится ровно 1 раз.

A) 1/3;

B) 0,432;

C) 0,288;

D) 0,216.

10. Вероятность наступления события A в каждом испытании равна 0,2. Вероятность

того, что в результате проведения 250 независимых испытаний событие A наступит

менее 80 раз, вычисляется:

A) по формуле Пуассона;

B) по интегральной формуле Лапласа;

C) по локальной формуле Муавра-Лапласа;

D) по формуле Бернулли.

11. Математическое ожидание алгебраической суммы двух случайных величин X и Y

находится по формуле:

A) M(X + Y) = M(X) + M(Y);

B) M(X + Y) = M(X) + M(Y) – M(X)·M(Y);

C) M(X + Y) = M(X) + M(Y) + M(X)·M(Y);

()

YXM +=+

ВАРИАНТ 17

12. Дискретная случайная величина X принимает значения 6, – 1, 2, – 5, 4 с равными

вероятностями. Математическое ожидание M(X) этой случайной величины равно:

A) 1,4;

B) 1,5;

C) 1,2;

D) 2.

13. Найти математическое ожидание случайной величины Z = 2(2X – 6), если известно

математическое ожидание случайной величины X: M(X) = 4.

A) 8;

B) 4;

C) 2;

D) 16.

14. Случайная величина X задана интегральной функцией:

()

⎪

⎩

⎪

⎨

⎧

≤<

≤

.4при1

;40при

0;при0

Найти вероятность того, что в результате испытания X примет значение, заключенное в

интервале (2, 3).

A) 7/16;

B) 5/16;

C) 1/16;

D) 1/2.

15. Дана дифференциальная функция случайной величины X:

()

⎪

⎩

⎪

⎨

⎧

≤<−

≤

.2при0

;21при5,0

;1при0

Найти вероятность того, что в результате испытания X примет значение, заключенное в

интервале (1,5; 2).

A) 1/8;

B) 5/8;

C) 3/8;

D) 7/8.

16. Случайная величина X задана интегральной функцией:

() ( )

⎪

⎩

⎪

⎨

⎧

≤<−

≤

.при1

;3при3

3;при0

Коэффициент β равен:

A) 8;

B) 6;

C) 5;

D) 4.

17. Найти моду статистической выборки

5, 2, 5, 3, 1, 1, 3, 2, 2.

A) 5;

B) 3;

C) 1;

D) 2.

18. Если основная гипотеза имеет вид H

: a = 5, то конкурирующей может быть

гипотеза:

A) Н

: a ≤ 5;

B) Н

: a ≠ 4;

C) Н

: a ≥ 5;

D) Н

: a ≠ 5.

19. Точечная оценка математического ожидания случайной величины, распределенной

по нормальному закону, равна 7,5. Тогда его интервальная оценка может быть записана

в виде:

A) (7; 9);

B) (6; 8);

C) (5; 10);

D) (6; 10).

20. Из генеральной совокупности извлечена выборка объема n = 110, полигон

относительных частот которой имеет вид

10 15 20

Тогда число вариант x

= 5 в выборке равно:

A) 11;

B) 22;

C) 20;

D) 15;

21. Выборочное уравнение парной регрессии имеет вид y = 4 + 3x. Тогда выборочный

коэффициент корреляции может быть равен:

A) – 0,7;

B) 3;

C) 0,7;

D) 1,5.

Экзаменационные тесты (ряды, теория вероятностей, математическая статистика) Составитель: Лаврусь О.Е.

Лаврусь В.В.

ВАРИАНТ 18

1. Радикальный признак Коши для знакоположительного числового ряда

∑

∞

определяется формулой:

∞→

lim

;

∞→

lim

;

∞→

lim

;

∞→

lim

2. Второй член ряда

()

∑

∞

−⋅

−

равен:

A) 1;

B) – 3/2;

C) 2/3;

D) – 2/3.

3. Общий член ряда

1 +−

… равен:

()

∑

∞

−

;

()

∑

∞

−

;

()

∑

∞

−

;

()

∑

∞

−

4. Сумма первых трех членов ряда

()

∑

∞

−

⋅−

равна:

A) –

120

; B)

120

; C)

120

; D) –

120

5. Найти интервал сходимости функционального ряда

()

∑

∞

A) – 6 < x < 6;

B) – 8 < x < 4;

C) – 4 < x < 8;

D) – 2 < x < 2.

6. Вероятность Р(А) появления случайного события А определяется из условия:

A) 0 ≤ Р(А) ≤ 1;

B) Р(А) < 1;

C) Р(А) = 0;

D) Р(А) = 1.

7. Формула Бернулли имеет вид:

()

nmmm

qpCmP

−

⋅⋅= ;

()

mmnm

qpCmP ⋅⋅=

−

;

()

nmm

qpCmP ⋅⋅= ;

()

mnmm

qpCmP

−

⋅⋅= .

8. Брошены две игральные кости. Найти вероятность того, что сумма очков на

выпавших гранях меньше 5.

A) 1/9;

B) 5/18;

C) 1/6;

D) 5/36.

9. Испытывается каждый из 6 элементов некоторого устройства. Вероятность того, что

элемент не выдержит испытания, равна 0,3. Найти наивероятнейшее число элементов,

которые выдержат испытание.

A) 3;

B) 5;

C) 4;

D) 2.

10. При исследовании всхожести семян установлено, что в среднем прорастают 85 семян

из 100. Вероятность того, что из 2000 семян прорастет ровно 1800, вычисляется:

A) по формуле Пуассона;

B) по локальной формуле Лапласа;

C) по интегральной формуле Муавра-Лапласа;

D) по формуле Бернулли.

11. Математическое ожидание произведения двух случайных величин X и Y находится

по формуле:

A) M(XY) = M(X) + M(Y);

B) M(XY) = M(X) – M(Y);

C) M(XY) = M(X)·M(Y);

()

XYM =

ВАРИАНТ 18

12. Дискретная случайная величина X задана законом распределения:

– 2 0 3

0,5 0,4

Дисперсия D(X) этой случайной величины равна:

A) 2,1;

B) 1,4;

C) 4;

D) 1.

13. Найти математическое ожидание случайной величины Z = 3X – Y, если известны

законы распределения независимых случайных величин X и Y:

0 2 5

0 4 6

0,1 0,5 0,4

0,4 0,3 0,3

A) 9;

B) 8;

C) 6;

D) 7.

14. Случайная величина X задана интегральной функцией:

()

⎪

⎩

⎪

⎨

⎧

≤<−+

−≤

.0при1

;03при

3;при0

Найти вероятность того, что в результате испытания X примет значение, заключенное в

интервале (– 2, 0).

A) 2/3;

B) 1/3;

C) 1/2;

D) 3/4.

15. Дана дифференциальная функция случайной величины X:

()

⎪

⎩

⎪

⎨

⎧

≤<

≤

.5при0

;50при2,0

;0при0

Найти вероятность того, что в результате испытания X примет значение, заключенное в

интервале (1, 3).

A) 3/5;

B) 1/5;

C) 2/5;

D) 4/5.

16. Дана дифференциальная функция случайной величины X:

()

⎪

⎩

⎪

⎨

⎧

≤<

≤

.1при0

;10при

;0при0

Коэффициент γ равен:

A) 2;

B) 3;

C) 4;

D) 5.

17. Найти моду статистической выборки

1, 3, 1, 3, 6, 4, 6, 3, 4.

A) 6;

B) 4;

C) 3;

D) 1.

18.. Если основная гипотеза имеет вид H

: a = 7, то конкурирующей может быть

гипотеза:

A) Н

: a ≠ 6;

B) Н

: a ≥ 7;

C) Н

: a ≠ 7;

D) Н

: a ≤ 7.

19. Точечная оценка математического ожидания случайной величины, распределенной

по нормальному закону, равна 6,5. Тогда его интервальная оценка может быть записана

в виде:

A) (5,3; 7,8);

B) (5,5; 8);

C) (5,6; 7,4);

D) (5; 7).

20. Из генеральной совокупности извлечена выборка объема n = 70, полигон

относительных частот которой имеет вид

12 18 24

Тогда число вариант x

= 18 в выборке равно:

A) 7;

B) 14;

C) 12;

D) 18;

21. Выборочное уравнение парной регрессии имеет вид y = – 1,2x + 6. Тогда выборочный

коэффициент корреляции может быть равен:

A) 0;

B) – 0,8;

C) – 1,2;

D) – 5.

Экзаменационные тесты (ряды, теория вероятностей, математическая статистика) Составитель: Лаврусь О.Е.

Лаврусь В.В.

ВАРИАНТ 19

1. Знаменатель геометрической прогрессии 1, 5, 25, 125… равен:

A) 4;

B) 5;

C) 25;

D) 3.

2. Первые три члена ряда

()

∞

−⋅

∑

имеют вид:

−+−

;

+−

;

−+

3. Общий член ряда

−+−

+ … равен:

()

∑

∞

−

;

()

∑

∞

−

;

()

∑

∞

−

;

()

∑

∞

−

4. Сумма первых трех членов ряда

()

∑

∞

−

равна:

105

; B)

105

; C) –

105

; D)

105

5. Найти интервал сходимости функционального ряда

()

∑

∞

−

A) – 6 < x < 6;

B) – 8 < x < 4;

C) – 4 < x < 8;

D) – 2 < x < 2.

6. Вероятность совместного появления двух независимых событий А и В равна:

A) Р(АВ) = Р(А)·Р(В);

B) Р(АВ) = Р(А) + Р(В);

C) Р(АВ) = Р(А)·Р(В) + Р(А – В);

D) Р(АВ) = Р(А)·Р(В) – Р(А + В).

7. Формула Пуассона имеет вид:

()

−

⋅

;

()

−

⋅

;

()

−

⋅

;

()

−

⋅

8. Брошены две игральные кости. Найти вероятность того, что сумма очков на

выпавших гранях равна 6.

A) 1/18;

B) 5/36;

C) 1/9;

D) 1/12.

9. Вероятность появления события А в одном испытании равна 0,5. Найти вероятность

того, что в четырех независимых испытаниях событие А появится ровно 3 раза.

A) 1/2;

B) 3/8;

C) 3/4;

D) 1/4.

10. В результате статистических исследований установлено, что в среднем 2 человека из

100 живут более 90 лет. Вероятность того, что среди 1000 человек, выбранных

случайным образом, более 15 окажется в возрасте более 90 лет, вычисляется:

A) по формуле Пуассона;

B) по локальной формуле Лапласа;

C) по интегральной формуле Муавра-Лапласа;

D) по формуле Бернулли.

11. Функция распределения F(x) = P(X < x), выражающая для каждого значения x

вероятность того, что случайная величина X примет значение, меньшее x, обладает

следующим свойством:

A) F(x) ≥ 0;

B) – ∞ < F(x) < + ∞;

C) 0< F(x) < + ∞;

D) 0 ≤ F(x) ≤ 1.

ВАРИАНТ 19

12. Дискретная случайная величина X задана законом распределения:

1 x

0,2 0,5 0,3

Если известно, что ее математическое ожидание M(X) равно 5,6, то x

равно:

A) 4;

B) 6;

C) 5;

D) 7.

13. Найти математическое ожидание случайной величины Z = 2(3X – 5), если известно

математическое ожидание случайной величины X: M(X) = 3.

A) 8;

B) 4;

C) 2;

D) 10.

14. Случайная величина X задана интегральной функцией:

()

⎪

⎩

⎪

⎨

⎧

≤<−

≤

.9при1

;96при2

6;при0

Найти вероятность того, что в результате испытания X примет значение, заключенное в

интервале (6, 8).

A) 3/4;

B) 1/3;

C) 2/3;

D) 1/4.

15. Дана дифференциальная функция случайной величины X:

()

⎪

⎩

⎪

⎨

⎧

≤<

≤

.2при0

;20при5,0

;0при0

Найти вероятность того, что в результате испытания X примет значение, заключенное в

интервале (1, 2).

A) 1/4;

B) 1/2;

C) 15/16;

D) 3/4.

16. Случайная величина X задана интегральной функцией:

()

⎪

⎩

⎪

⎨

⎧

≤<+

≤

.0при1

;0при13

;при0

Коэффициент α равен:

A) – 1/2;

B) – 1;

C) – 2/3;

D) – 1/3.

17. Найти моду статистической выборки

7, 8, 4, 7, 3, 3, 8, 7, 4.

A) 8;

B) 7;

C) 4;

D) 3.

18. Если основная гипотеза имеет вид H

: a = 6, то конкурирующей может быть

гипотеза:

A) Н

: a ≠ 5;

B) Н

: a < 6;

C) Н

: a ≥ 6;

D) Н

: a ≤ 6.

19. Точечная оценка математического ожидания случайной величины, распределенной

по нормальному закону, равна 5,5. Тогда его интервальная оценка может быть записана

в виде:

A) (4; 6);

B) (5; 7);

C) (4,5; 6);

D) (4,5; 6,5).

20. Из генеральной совокупности извлечена выборка объема n = 60, полигон

относительных частот которой имеет вид

234

Тогда число вариант x

= 4 в выборке равно:

A) 20;

B) 16;

C) 18;

D) 12;

21. Выборочное уравнение парной регрессии имеет вид y = – 0,8 + 2x. Тогда выборочный

коэффициент корреляции может быть равен:

A) – 0,8;

B) 2;

C) – 0,4;

D) 0,8.