Лапин И.А., Ратафьева Л.С. Кратные интегралы. Теория поля
Подождите немного. Документ загружается.


31
(,,)
kkk k
xyz S
ρ
⋅Δ , „‰Â
k
SΔ – ÔÎÓ˘‡‰¸ k -È fl˜ÂÈÍË; ÚÓ„‰‡ χÒÒ‡ ‚ÒÂÈ
ÔÓ‚ÂðıÌÓÒÚË
S :
11
(,,)
nn
kkkkk
kk
Mm xyzS
ρ
==
=
Δ≈ Δ
∑∑
.
ëÔð‡‚‡ Á‰ÂÒ¸ ÒÚÓËÚ ËÌÚ„ð‡Î¸Ì‡fl ÒÛÏχ ‰Îfl ÌÂÔðÂð˚‚ÌÓÈ ÙÛÌÍ-
ˆËË. àÁÏÂθ˜‡fl ‰ðÓ·ÎÂÌËÂ Ë ÛÒÚðÂÏÎflfl ð‡Ì„ ‰ðÓ·ÎÂÌËfl Í ÌÛβ, ‚
Ôð‰ÂΠÔÓÎÛ˜ËÏ Ú‡ÍÛ˛ ÙÓðÏÛÎÛ ‰Îfl ‚˚˜ËÒÎÂÌËfl χÒÒ˚ ÔÓ‚ÂðıÌÓ-
ÒÚË
S :
22
1(,,) (,) (,)
D
M x y z p x y q x y dxdy
ρ
=++
∫∫
.
Ç ˜‡ÒÚÌÓÒÚË, ÂÒÎË ÔÓ‚ÂðıÌÓÒÚ¸
S ÎÂÊËÚ ‚ ÔÎÓÒÍÓÒÚË xOy , Ú.Â.
ÒÓ‚Ô‡‰‡ÂÚ Ò Ó·Î‡ÒÚ¸˛
D , ÚÓ (,)
D
D
Mxydxdy
ρ
=
∫
∫
.
5. Ç˚˜ËÒÎÂÌË χÒÒ˚ Ú·.
ÖÒÎË ‚ ͇ʉÓÈ ÚӘ͠Ú·
T , Ó„ð‡Ì˘ÂÌÌÓ„Ó ÔðÓÒÚÓÈ ÔÓ‚ÂðıÌÓ-
ÒÚ¸˛, Á‡‰‡Ì‡ ÔÎÓÚÌÓÒÚ¸
(,,)xyz
ρ
ρ
=
, „‰Â
ρ
– ÌÂÔðÂð˚‚̇fl ÙÛÌÍ-
ˆËfl ‚ ͇ʉÓÈ ÚӘ͠Ú·
T
, ÚÓ, Ôðӂ‰fl ‡Ì‡Îӄ˘Ì˚ ð‡ÒÒÛʉÂ-
ÌËfl, ÔÓÎÛ˜ËÏ, ˜ÚÓ Ï‡ÒÒ‡ Ú· ð‡‚̇
(,,)
D
D
M x y z dxdydz
ρ
=
∫
∫∫
.
6. åÓÏÂÌÚ˚ ÔÎÓÒÍÓÈ ÙË„Ûð˚.
àÁ ÍÛðÒÓ‚ ÚÂÓðÂÚ˘ÂÒÍÓÈ ÏÂı‡ÌËÍË ËÁ‚ÂÒÚÌÓ, ˜ÚÓ ÒÚ‡Ú˘ÂÒÍËÏ
ÏÓÏÂÌÚÓÏ
l
S
χÚÂðˇθÌÓÈ ÚÓ˜ÍË Ï‡ÒÒ˚ m ÓÚÌÓÒËÚÂθÌÓ ÓÒË l ̇-
Á˚‚‡ÂÚÒfl ÔðÓËÁ‚‰ÂÌË χÒÒ˚ ˝ÚÓÈ ÚÓ˜ÍË Ì‡ ð‡ÒÒÚÓflÌË ‰Ó ÓÒË
l ,
Ú.Â.
ll
Smr
=
.
åÓÏÂÌÚÓÏ ËÌÂðˆËË
l
I χÚÂðˇθÌÓÈ ÚÓ˜ÍË ÓÚÌÓÒËÚÂθÌÓ ÓÒË l
̇Á˚‚‡ÂÚÒfl ÔðÓËÁ‚‰ÂÌË χÒÒ˚
m ˝ÚÓÈ ÚÓ˜ÍË Ì‡ Í‚‡‰ð‡Ú  ð‡Ò-
ÒÚÓflÌËfl ‰Ó ÓÒË
l , Ú.Â.
2
ll
Imr= .

32
ëÚ‡Ú˘ÂÒÍËÏ ÏÓÏÂÌÚÓÏ ÒËÒÚÂÏ˚ χÚÂðˇθÌ˚ı ÚÓ˜ÂÍ ÓÚÌÓÒË-
ÚÂθÌÓ ÓÒË
l ̇Á˚‚‡ÂÚÒfl ÒÛÏχ ÒÚ‡Ú˘ÂÒÍËı ÏÓÏÂÌÚÓ‚ ÓÚÌÓÒËÚÂθÌÓ
˝ÚÓÈ ÓÒË ‚ÒÂı χÚÂðˇθÌ˚ı ÚÓ˜ÂÍ, ‚ıÓ‰fl˘Ëı ‚ ÒËÒÚÂÏÛ.
èÛÒÚ¸ ‚ ÔÎÓÒÍÓÈ Ó·Î‡ÒÚË
D ð‡ÒÔð‰ÂÎÂ̇ χÒÒ‡ Ò ÔÎÓÚÌÓÒÚ¸˛
(,)xy
ρ
. ê‡ÁÓ·¸ÂÏ Ó·Î‡ÒÚ¸
D
̇
n
˜‡ÒÚÂÈ, „‰Â
k
S
Δ
– ÔÎÓ˘‡‰¸
k
-È
fl˜ÂÈÍË (
12, ,...,kn= ). Ç fl˜ÂÈÍÂ
k
D ‚ÓÁ¸ÏÂÏ ÔðÓËÁ‚ÓθÌÛ˛ ÚÓ˜ÍÛ
(,)
kk
xy , ÚÓ„‰‡ ‚ ÒËÎÛ Ò‰Â·ÌÌÓ„Ó ‚˚¯Â ÓÔð‰ÂÎÂÌËfl ÏÓÊÂÏ Ò˜ËÚ‡Ú¸,
˜ÚÓ
1
(,)
n
xkkkk
k
SxyyS
ρ
=
≈⋅⋅Δ
∑
;
1
(,)
n
ykkkk
k
SxyxS
ρ
=
≈
⋅⋅Δ
∑
.
àÁÏÂθ˜‡fl ‰ðÓ·ÎÂÌËÂ, ‚ Ôð‰ÂΠÔÓÎÛ˜ËÏ ÚÓ˜Ì˚ Á̇˜ÂÌËfl ‰Îfl
ÒÚ‡Ú˘ÂÒÍËı ÏÓÏÂÌÚÓ‚ ӷ·ÒÚË
D ÓÚÌÓÒËÚÂθÌÓ ÓÒÂÈ Ox Ë Oy :
(,)
x
D
Sxyydxdy
ρ
=
∫
∫
;
(,)
y
D
S x y x dxdy
ρ
=
∫
∫
.
èðÓ‚Ó‰fl ‡Ì‡Îӄ˘Ì˚ ð‡ÒÒÛʉÂÌËfl ‰Îfl ÏÓÏÂÌÚÓ‚ ËÌÂðˆËË Ó·-
·ÒÚË ÓÚÌÓÒËÚÂθÌÓ ÍÓÓð‰Ë̇ÚÌ˚ı ÓÒÂÈ, ÔÓÎÛ˜ËÏ:
2
(,)
x
D
I x y y dxdy
ρ
=
∫
∫
;
2
(,)
y
D
I x y x dxdy
ρ
=
∫
∫
.
7. äÓÓð‰Ë̇Ú˚ ˆÂÌÚð‡ χÒÒ.
èÛÒÚ¸
D – ÔÎÓÒ͇fl ӷ·ÒÚ¸, ‚ ÍÓÚÓðÓÈ ð‡ÒÔð‰ÂÎÂ̇ χÒÒ‡ Ò
ÔÎÓÚÌÓÒÚ¸˛
(,)xy
ρ
. èÓ ÓÔð‰ÂÎÂÌ˲ ˆÂÌÚðÓÏ Ï‡ÒÒ ÔÎÓÒÍÓÈ Ó·Î‡ÒÚË
̇Á˚‚‡ÂÚÒfl ÚӘ͇
C Ò ÍÓÓð‰Ë̇ڇÏË:
y
C
S
x
M
=
,
x
C
S
y
M
=
,
„‰Â
M
– χÒÒ‡ ÔÎÓÒÍÓÈ Ó·Î‡ÒÚË
D
, ‡
x
S Ë
y
S – ÒÚ‡Ú˘ÂÒÍË ÏÓ-
ÏÂÌÚ˚.
èðËÌËχfl ‚Ó ‚ÌËχÌË ‚˚ð‡ÊÂÌËfl ‰Îfl χÒÒ˚ Ë ÒÚ‡Ú˘ÂÒÍËı
ÏÓÏÂÌÚÓ‚ ˜ÂðÂÁ ‰‚ÓÈÌ˚ ËÌÚ„ð‡Î˚, ÔÓÎÛ˜ËÏ:
(,)
(,)
D
C
D
xyxdxdy
x
xydxdy
ρ
ρ
=
∫∫
∫∫
,
(,)
(,)
D
C
D
xyydxdy
y
xydxdy
ρ
ρ
=
∫∫
∫∫
.
33
ê‡ÒÒÏÓÚðËÏ ÚÂÔÂð¸ ÌÂÍÓÚÓðÓ ÚÂÎÓ
T , Ó„ð‡Ì˘ÂÌÌÓ ÔðÓÒÚÓÈ ÔÓ-
‚ÂðıÌÓÒÚ¸˛, Ë ÔÛÒÚ¸ ‚ ÌÂÏ ð‡ÒÔð‰ÂÎÂ̇ χÒÒ‡, ÔÎÓÚÌÓÒÚ¸ ÍÓÚÓðÓÈ
(,,)xyz
ρ
, ÚÓ„‰‡ ‰Îfl ÍÓÓð‰ËÌ‡Ú ˆÂÌÚð‡ χÒÒ ˝ÚÓ„Ó Ú· ÔÓÎÛ˜ËÏ ÒÓ-
‚Âð¯ÂÌÌÓ ‡Ì‡Îӄ˘Ì˚ ‚˚ð‡ÊÂÌËfl:
(,)
(,)
T
C
T
xyxdv
x
xydv
ρ
ρ
=
∫∫∫
∫∫∫
,
(,)
(,)
T
C
T
xyydv
y
xydv
ρ
ρ
=
∫∫∫
∫∫∫
,
(,)
(,)
T
C
T
xyzdv
z
xydv
ρ
ρ
=
∫∫∫
∫∫∫
.
§4. äðË‚ÓÎËÌÂÈÌ˚ ÍÓÓð‰Ë̇Ú˚ Ë Á‡ÏÂ̇ ÔÂðÂÏÂÌÌ˚ı ‚
Íð‡ÚÌ˚ı ËÌÚ„ð‡Î‡ı
1. äðË‚ÓÎËÌÂÈÌ˚ ÍÓÓð‰Ë̇Ú˚.
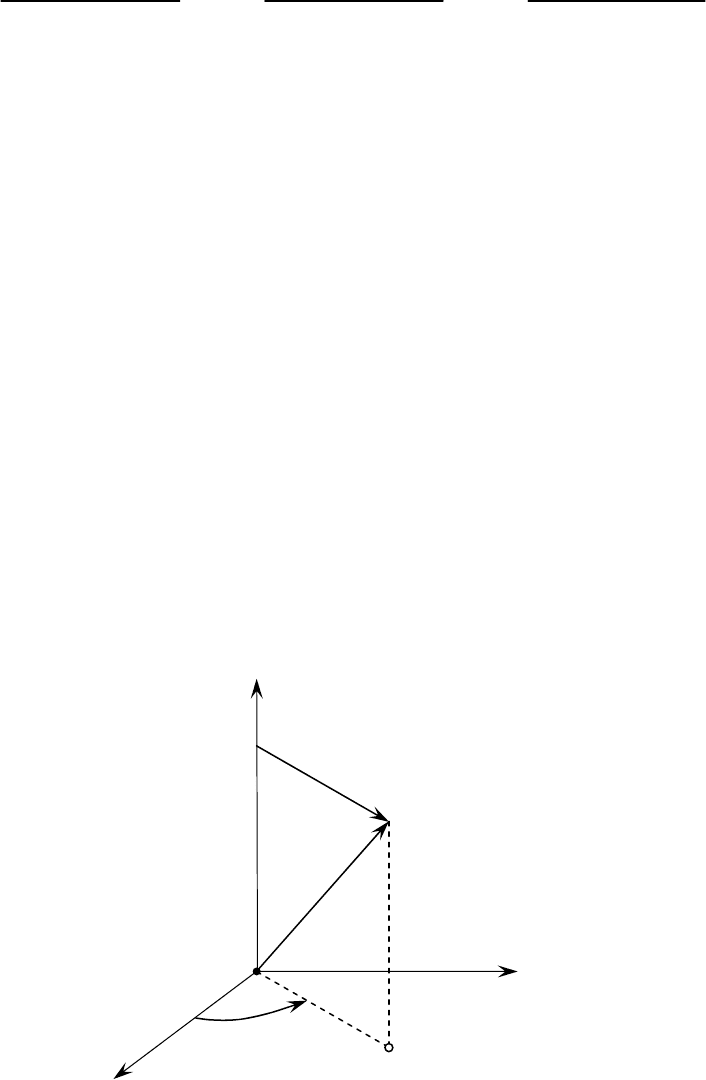
éÚÌÓÒËÚÂθÌÓ ÔðÓÒÚð‡ÌÒÚ‚ÂÌÌÓÈ ‰Â͇ðÚÓ‚ÓÈ ÒËÒÚÂÏ˚ ÍÓÓð‰Ë̇Ú
Oxyz
ÔÓÎÓÊÂÌË ÚÓ˜ÍË
M
ÓÔð‰ÂÎflÂÚÒfl  ÚðÂÏfl ‰Â͇ðÚÓ‚˚ÏË
ÍÓÓð‰Ë̇ڇÏË
x , y Ë z . ÖÒÎË 0z > , ÚÓ ÔÓÎÓÊÂÌË ÚÓ˜ÍË M ÏÓÊ-
ÌÓ ÓÔð‰ÂÎËÚ¸, Á‡‰‡‚ ÚðË Ô‡ð‡ÏÂÚð‡:
ρ
– ð‡ÒÒÚÓflÌË ÚÓ˜ÍË M ÓÚ
ÓÒË
Oz
;
r
– ð‡ÒÒÚÓflÌË ÚÓ˜ÍË
M
ÓÚ Ì‡˜‡Î‡ ÍÓÓð‰Ë̇Ú;
ϕ
– ‰‚Ûı-
„ð‡ÌÌ˚È Û„ÓÎ ÏÂÊ‰Û ÔÎÓÒÍÓÒÚ¸˛
xOz Ë ÔÎÓÒÍÓÒÚ¸˛, ÔðÓıÓ‰fl˘ÂÈ
˜ÂðÂÁ ÓÒ¸
Oz Ë ÚÓ˜ÍÛ M (ðËÒ. 1.4.1).
êËÒ. 1.4.1
x
y
z
0
M
ρ
r
ϕ

34
é˜Â‚ˉÌÓ, ˜ÚÓ Ô‡ð‡ÏÂÚð˚
ρ
, r Ë
ϕ
ÏÓÊÌÓ ‚˚ð‡ÁËÚ¸ ˜ÂðÂÁ ‰Â-
͇ðÚÓ‚˚ ÍÓÓð‰Ë̇Ú˚
x , y Ë z . è‡ð‡ÏÂÚð˚
ρ
, r Ë
ϕ
Ï˚ ÏÓÊÂÏ
Ú‡ÍÊ ̇Á‚‡Ú¸ ÍÓÓð‰Ë̇ڇÏË ÚÓ˜ÍË
M , Ôð˘ÂÏ
0
ρ
≤
<+∞, 0 r
≤
<+∞, 02
ϕ
π
≤
< .
à ‚ÓÓ·˘Â, Á‡ ÍÓÓð‰Ë̇Ú˚ ÚÓ˜ÍË
M Ï˚ ÏÓÊÂÏ ÔðËÌflÚ¸ β·˚ ÚðË
ÙÛÌ͈ËË:
(,,)xyz
ξ
ξ
= , (,,)xyz
η
η
=
, (,,)xyz
ζ
ζ
=
,
Î˯¸ ·˚ ÚÓθÍÓ ÒÓÓÚÌÓ¯ÂÌËflÏË (1) ÍÓÓð‰Ë̇Ú˚
x , y Ë z ÓÔð‰Â-
ÎflÎËÒ¸ Ó‰ÌÓÁ̇˜ÌÓ:
(,, )xx
ξ
ηζ
= , (,, )yy
ξ
ηζ
=
, (,, )zz
ξ
ηζ
=
,
Ú.Â. ÌË Ó‰ÌÓ ËÁ ÒÓÓÚÌÓ¯ÂÌËÈ (1) ËÎË (2) Ì ‰ÓÎÊÌÓ ÔðÓÚË‚Óð˜ËÚ¸
‰ðÛ„ËÏ ËÎË ·˚Ú¸ ÒΉÒÚ‚ËÂÏ ‰ðÛ„Ëı. á‡ÏÂÚËÏ, ˜ÚÓ ËÁ ÒÓÓÚÌÓ¯ÂÌËÈ
(2) ‚ ˝ÚÓÏ ÒÎÛ˜‡Â Ô‡ð‡ÏÂÚð˚
ξ
,
η
Ë
ζ
Ú‡ÍÊ ·Û‰ÛÚ ÓÔð‰ÂÎflÚ¸Òfl
Ó‰ÌÓÁ̇˜ÌÓ. åÓÊÌÓ ‰Ó͇Á‡Ú¸, ˜ÚÓ ˝ÚË ÛÒÎÓ‚Ëfl ‚˚ÔÓÎÌfl˛ÚÒfl, ÂÒÎË
ÓÔð‰ÂÎËÚ¸
(,, )J
ξ
ηζ
, ̇Á˚‚‡ÂÏ˚È ÓÔð‰ÂÎËÚÂÎÂÏ üÍÓ·Ë ËÎË
flÍӷˇÌÓÏ ÔðÂÓ·ð‡ÁÓ‚‡ÌËfl, ÓÚ΢ÂÌ ÓÚ ÌÛÎfl, Ú.Â.
0(,, )
xxx
Jyyy
zzz
ξηζ
ξηζ
ξηζ
ξηζ
′′′
′′′
=
≠
′′′
.
2. äÓÓð‰Ë̇ÚÌ˚ ÔÓ‚ÂðıÌÓÒÚË.
á‡ÙËÍÒËðÛÂÏ Í‡ÍÛ˛-ÌË·Û‰¸ ÍÓÓð‰Ë̇ÚÛ, ÓÔð‰ÂÎÂÌÌÛ˛ ÒÓÓÚÌÓ-
¯ÂÌËflÏË (1), ̇ÔðËÏÂð
ξ
, ÔÓÎÓÊË‚
1
c
ξ
=
, ÚÓ„‰‡ ÔÓÎÛ˜ËÏ
1
(,,)xyz c
ξ
= (ðËÒ. 1.4.2).
ë „ÂÓÏÂÚð˘ÂÒÍÓÈ ÚÓ˜ÍË ÁðÂÌËfl ˝ÚÓÏÛ Ûð‡‚ÌÂÌ˲ ‚ ÔðÓÒÚð‡ÌÒÚ‚Â
ÒÓÓÚ‚ÂÚÒÚ‚ÛÂÚ ÌÂÍÓÚÓð‡fl ÔÓ‚ÂðıÌÓÒÚ¸
ξ
. Ä̇Îӄ˘ÌÓ ÏÓÊÌÓ ÓÔðÂ-
‰ÂÎËÚ¸ ÍÓÓð‰Ë̇ÚÌ˚ ÔÓ‚ÂðıÌÓÒÚË
η
Ë
ζ
ÒÓÓÚ‚ÂÚÒÚ‚ÂÌÌÓ:
2
(,,)xyz c
η
= Ë
3
(,,)xyz c
ζ
=
.
(1)
(2)
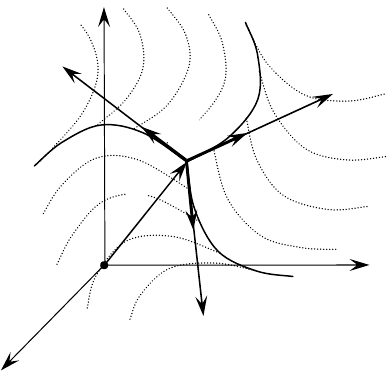
35
äÓÓð‰Ë̇ÚÌ˚ ÔÓ‚ÂðıÌÓÒÚË
1
c
ξ
=
,
2
c
η
=
Ë
3
c
ζ
= ÔðË Òӷβ‰Â-
ÌËË ÛÒÎÓ‚Ëfl (2) ÔÂðÂÒÂ͇˛ÚÒfl ‚ ÌÂÍÓÚÓðÓÈ ÚÓ˜ÍÂ
M . í‡ÍËÏ Ó·ð‡-
ÁÓÏ, ÚӘ͇
M ÓÔð‰ÂÎflÂÚÒfl Í‡Í ÚӘ͇ ÔÂðÂÒ˜ÂÌËfl ÍÓÓð‰Ë̇ÚÌ˚ı
ÔÓ‚ÂðıÌÓÒÚÂÈ (ðËÒ. 1.4.2).
3. äÓÓð‰Ë̇ÚÌ˚ ÎËÌËË.
ê‡ÒÒÏÓÚðËÏ ÔÂðÂÒ˜ÂÌËfl ‰‚Ûı ÍÓÓð‰Ë̇ÚÌ˚ı ÔÓ‚ÂðıÌÓÒÚÂÈ:
1
2
(,,)
(,,)
xyz c
xyz c
ξ
η
=
⎫
⎬
=
⎭
.
é˜Â‚ˉÌÓ, ˜ÚÓ ÍðË‚‡fl, ÔÓ ÍÓÚÓðÓÈ ÔÂðÂÒÂ͇˛ÚÒfl ˝ÚË ÔÓ‚ÂðıÌÓ-
ÒÚË, ӷ·‰‡ÂÚ Ú‡ÍËÏ Ò‚ÓÈÒÚ‚ÓÏ, ˜ÚÓ ‚‰Óθ ˝ÚÓÈ ÍðË‚ÓÈ ÍÓÓð‰Ë̇Ú˚
ξ
Ë
η
ÔÓÒÚÓflÌÌ˚, ‡ ÏÂÌflÂÚÒfl Ӊ̇ ÚÓθÍÓ ÍÓÓð‰Ë̇ڇ
ζ
, ÔÓ˝ÚÓÏÛ
˝Ú‡Í ÍðË‚‡fl ̇Á˚‚‡ÂÚÒfl ÍÓÓð‰Ë̇ÚÌÓÈ ÎËÌËÂÈ
ζ
. Ä̇Îӄ˘ÌÓ ÔÂ-
ðÂÒ˜ÂÌË ÔÓ‚ÂðıÌÓÒÚÂÈ
1
3
(,,)
(,,)
xyz c
xyz c
ξ
ζ
=
⎫
⎬
=
⎭
Ë
2
3
(,,)
(,,)
xyz c
xyz c
η
ζ
=
⎫
⎬
=
⎭
‰‡ÂÚ Ì‡Ï ÒÓÓÚ‚ÂÚÒÚ‚ÂÌÌÓ ÍÓÓð‰Ë̇ÚÌ˚ ÎËÌËË
η
Ë
ξ
.
é˜Â‚ˉÌÓ, ˜ÚÓ ‚ Ó·˘ÂÏ ÒÎÛ˜‡Â ÍÓÓð‰Ë̇ÚÌ˚ ÎËÌËË Ôð‰ÒÚ‡‚Îfl-
˛Ú ÒÓ·ÓÈ ÌÂÍÓÚÓð˚ ÍðË‚˚Â, ÔÓ˝ÚÓÏÛ ÍÓÓð‰Ë̇Ú˚
ξ
,
η
Ë
ζ
̇Á˚-
‚‡˛ÚÒfl ÍðË‚ÓÎËÌÂÈÌ˚ÏË ÍÓÓð‰Ë̇ڇÏË. èðӂ‰ÂÏ Í ÍÓÓð‰Ë̇ÚÌ˚Ï
ÎËÌËflÏ, ÔÂðÂÒÂ͇˛˘ËÏÒfl ‚ ÚÓ˜ÍÂ
M , ͇҇ÚÂθÌ˚Â, ̇Ôð‡‚ÎÂÌËfl
ÍÓÚÓð˚ı ÒÓÓÚ‚ÂÚÒÚ‚Û˛Ú Ì‡Ôð‡‚ÎÂÌËflÏ ‚ÓÁð‡ÒÚ‡ÌËfl ÍÓÓð‰Ë̇Ú. éð-
Ú˚ ˝ÚËı ÓÒÂÈ Ì‡Á˚‚‡˛ÚÒfl ÓðÚ‡ÏË ÍðË‚ÓÎËÌÂÈÌ˚ı ÍÓÓð‰Ë̇ÚÌ˚ı
ÓÒÂÈ Ë Ó·ÓÁ̇˜‡˛ÚÒfl ÒÓÓÚ‚ÂÚÒÚ‚ÂÌÌÓ
0
ξ
,
0
η
Ë
0
ζ
. ëËÒÚÂÏÛ ÍðË‚ÓÎË-
êËÒ. 1.4.2
x
y
0
z
0
ξ
ξ
0
ζ
ζ
η
0
η
r
1
c
ξ
=
ζ
к
.л.
ξ
к.л.
η
к
.л.
3
c
ζ
=
2
c
η
=
36
ÌÂÈÌ˚ı ÍÓÓð‰ËÌ‡Ú Ì‡Á˚‚‡˛Ú ÓðÚÓ„Ó̇θÌÓÈ, ÂÒÎË ÓðÚÓ„Ó̇θÌ˚
ÓðÚ˚
0
ξ
,
0
η
Ë
0
ζ
, Ú.Â. ‚˚ÔÓÎÌfl˛ÚÒfl ÛÒÎÓ‚Ëfl
00 00 00
0⋅⋅=⋅=ξη=ηζ ζξ .
á‡ÏÂÚËÏ, ˜ÚÓ ‚ ‰Â͇ðÚÓ‚ÓÈ ÒËÒÚÂÏ ÍÓÓð‰Ë̇Ú
Oxyz ÍÓÓð‰Ë̇Ú-
Ì˚ÏË ÔÓ‚ÂðıÌÓÒÚflÏË ·Û‰ÛÚ fl‚ÎflÚ¸Òfl ÔÎÓÒÍÓÒÚË, Ô‡ð‡ÎÎÂθÌ˚ ÍÓ-
Óð‰Ë̇ÚÌ˚Ï ÔÎÓÒÍÓÒÚflÏ
xOy , xOz Ë yOz , ‡ ÍÓÓð‰Ë̇ÚÌ˚ÏË ÎË-
ÌËflÏË – ÔðflÏ˚Â, Ô‡ð‡ÎÎÂθÌ˚ ÍÓÓð‰Ë̇ÚÌ˚Ï ÓÒflÏ
Ox , Oy Ë
Oz .
4. äÓ˝ÙÙˈËÂÌÚ˚ ã‡ÏÂ.
ê‡ÒÒÏÓÚðËÏ ‚ÂÍÚÓð
r
– ð‡‰ËÛÒ-‚ÂÍÚÓð ÚÓ˜ÍË
M
ÔÓ‚ÂðıÌÓÒÚÂÈ
(ðËÒ. 1.4.2). é˜Â‚ˉÌÓ, ˜ÚÓ ÔðÓËÁ‚Ӊ̇fl
r
ξ
∂
∂
ÎÂÊËÚ Ì‡ ͇҇ÚÂθÌÓÈ
Í „Ó‰Ó„ð‡ÙÛ ‚ÂÍÚÓð‡
r , ÔÓÒÚðÓÂÌÌÓÏÛ ‚ Ôð‰ÔÓÎÓÊÂÌËË, ˜ÚÓ ÏÂÌfl-
ÂÚÒfl ÚÓθÍÓ ÍÓÓð‰Ë̇ڇ
ξ
, ‡ ÍÓÓð‰Ë̇Ú˚
η
Ë
ζ
ÓÒÚ‡˛ÚÒfl ÌÂËÁÏÂÌ-
Ì˚ÏË; Ë Ì‡Ôð‡‚ÎÂ̇ ‚ ÒÚÓðÓÌÛ ‚ÓÁð‡ÒÚ‡ÌËfl ÍÓÓð‰Ë̇Ú˚
ξ
. é˜Â‚ˉ-
ÌÓ, ˜ÚÓ
0
rr
/
ξ
ξ
∂∂
=
∂∂
ξ
. Ä̇Îӄ˘ÌÓ
0
rr
/
η
η
∂
∂
=
∂
∂
η
,
0
rr
/
ζ
ζ
∂
∂
=
∂
∂
ζ
.
Ç˚ð‡ÊÂÌËfl
r
H
ξ
ξ
∂
=
∂
,
r
H
η
η
∂
=
∂
Ë
r
H
ζ
ζ
∂
=
∂
̇Á˚‚‡˛ÚÒfl ÍÓ˝Ù-
ÙˈËÂÌÚ‡ÏË ã‡ÏÂ. í‡Í Í‡Í ð‡‰ËÛÒ-‚ÂÍÚÓð ÚÓ˜ÍË
M ð‡‚ÂÌ
ri
j
kxyz=++ , ÚÓ, ‚˚ÔÓÎÌflfl ‰ËÙÙÂðÂ̈ËðÓ‚‡ÌËÂ, ÔÓÎÛ˜ËÏ
r
i
j
k
r
i
j
k
r
i
j
k
xyz
xyz
xyz
ξξ ξ ξ
ηη η η
ζζ ζ ζ
⎫
∂∂ ∂ ∂
=++
⎪
∂∂ ∂ ∂
⎪
⎪
∂∂ ∂ ∂
=++
⎬
∂∂ ∂ ∂
⎪
⎪
∂∂ ∂ ∂
=++
⎪
∂∂ ∂ ∂
⎭
.
èðËÌËχfl ‚Ó ‚ÌËχÌË ˝ÚË ÒÓÓÚÌÓ¯ÂÌËfl, ÌÂÚðÛ‰ÌÓ ÔÓÎÛ˜ËÚ¸
Ú‡ÍË ‚˚ð‡ÊÂÌËfl ‰Îfl ÍÓ˝ÙÙˈËÂÌÚÓ‚ ã‡ÏÂ:
222
222
222
Hxyz
Hxyz
Hxyz
ξξξξ
ηηηη
ζζζζ
⎫
′
′′
=++
⎪
⎪
⎪
′
′′
=++
⎬
⎪
⎪
′
′′
=++
⎪
⎭
.
(3)
(4)
37
èðËÏÂÏ ‚Ó ‚ÌËχÌË ÒÓÓÚÌÓ¯ÂÌËfl (3) Ë (4), ÚÓ„‰‡ ‚˚ð‡ÊÂÌËfl
‰Îfl ÓðÚÓ‚ ÍðË‚ÓÎËÌÂÈÌ˚ı ÍÓÓð‰ËÌ‡Ú Á‡Ô˯ÛÚÒfl Ú‡Í:
(
)
(
)
(
)
0222
0222
0222
i
j
k/ ;
i
j
k/ ;
i
j
k/ .
xyz x y z
xyz x y z
xyz x y z
ξξξ ξ ξ ξ
ηηη η η η
ζζζ ζ ζ ζ
′′′ ′ ′ ′
=++ ++
′
′′ ′ ′ ′
=++ ++
′
′′ ′ ′ ′
=++ ++
ξ
η
ζ
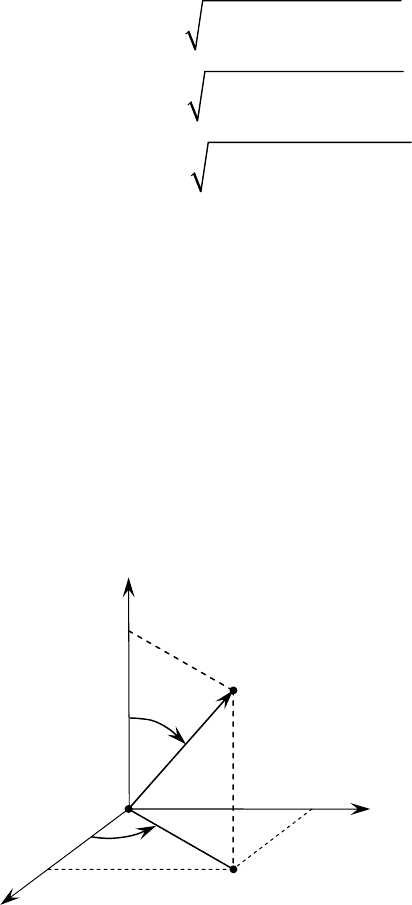
5. ëÙÂð˘ÂÒÍË ÍÓÓð‰Ë̇Ú˚.
ëÙÂð˘ÂÒÍËÏË ÍÓÓð‰Ë̇ڇÏË
M ÚÓ˜ÍË Ì‡Á˚‚‡˛ÚÒfl Ô‡ð‡ÏÂÚð˚
ρ
,
θ
Ë
ψ
(ðËÒ. 1.4.3), „‰Â
ρ
– ð‡ÒÒÚÓflÌË ÓÚ ÚÓ˜ÍË M ‰Ó ̇˜‡Î‡ ÍÓÓð‰ËÌ‡Ú (0
ρ
≤<+∞);
θ
– Û„ÓÎ, ÓÚÒ˜ËÚ˚‚‡ÂÏ˚È ÓÚ ÓÒË Oz ‰Ó ‚ÂÍÚÓð‡
ρ
ur
(0
θ
π
≤<);
ψ
– Û„ÓÎ, ÏÂÊ‰Û ÔÎÓÒÍÓÒÚ¸˛
xOz
Ë ÔÎÓÒÍÓÒÚ¸˛, ÔðÓıÓ‰fl˘ÂÈ
˜ÂðÂÁ ÚÓ˜ÍÛ
M
Ë ÓÒ¸
Oz
(
02
ψ
π
≤
<
).
é˜Â‚ˉÌÓ, ˜ÚÓ ‚ ÒÙÂð˘ÂÒÍËı ÍÓÓð‰Ë̇ڇı ÍÓÓð‰Ë̇ÚÌ˚ÏË ÔÓ-
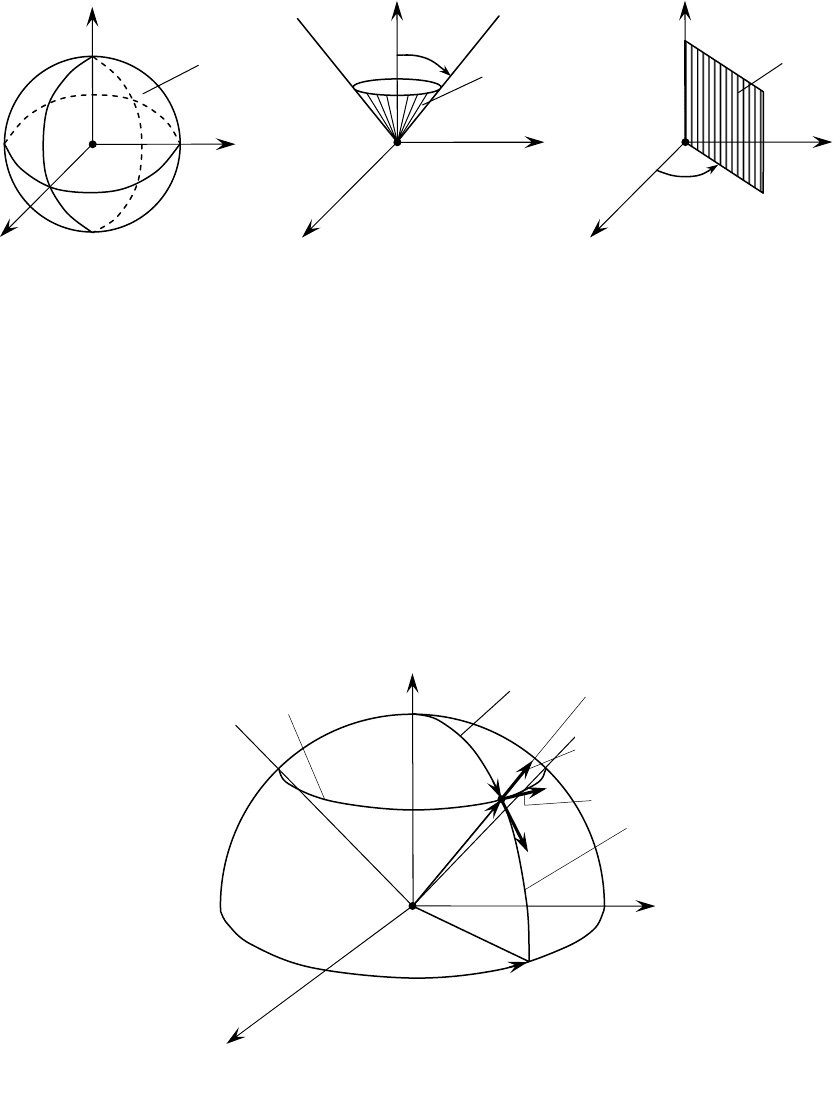
‚ÂðıÌÓÒÚflÏË fl‚Îfl˛ÚÒfl Ú‡ÍË ÔÓ‚ÂðıÌÓÒÚË:
1
c
ρ
= – ÒÙÂð‡ ð‡‰ËÛÒ‡
1
c ˆÂÌÚðÓÏ ‚ ̇˜‡Î ÍÓÓð‰ËÌ‡Ú (ðËÒ.
1.4.4 ‡);
2
c
θ
= – ÍÓÌÛÒ Ò ‚Âð¯ËÌÓÈ ‚ ̇˜‡Î ÍÓÓð‰Ë̇Ú, Ó·ð‡ÁÛ˛˘Ë ÍÓ-
ÚÓðÓ„Ó ÒÓÒÚ‡‚Îfl˛Ú Û„ÓÎ
2
c
θ
=
Ò ÓÒ¸˛
Oz
(ðËÒ. 1.4.4 ·);
3
c
ψ
= – ÔÎÓÒÍÓÒÚ¸, ÔðÓıÓ‰fl˘‡fl ˜ÂðÂÁ ÓÒ¸ Oz Ë Ó·ð‡ÁÛ˛˘‡fl
Û„ÓÎ
3
c
ψ
=
Ò ÍÓÓð‰Ë̇ÚÌÓÈ ÔÎÓÒÍÓÒÚ¸˛ Oz (ðËÒ. 1.4.4 ‚).
êËÒ. 1.4.3
x
y
z
0
(,,
)
Mxyz
ρ
u
r
ψ
θ
x
y
z
M
′
38
ëÙÂð‡
1
c
ρ
= Ë ÍÓÌÛÒ
2
c
θ
= ÔÂðÂÒÂ͇˛ÚÒfl ÔÓ ÓÍðÛÊÌÓÒÚË, ÍÓÚÓ-
ð‡fl Ôð‰ÒÚ‡‚ÎflÂÚ ÒÓ·ÓÈ ÍÓÓð‰Ë̇ÚÌÛ˛ ÎËÌ˲
ψ
. ëÙÂð‡
1
c
ρ
= Ë
ÔÎÓÒÍÓÒÚ¸
3
c
ψ
=
ÔÂðÂÒÂ͇˛ÚÒfl ÔÓ ÓÍðÛÊÌÓÒÚË (ÍÓÓð‰Ë̇Ú̇fl ÎË-
ÌËfl
θ
). äÓÌÛÒ
2
c
θ
= Ë ÔÎÓÒÍÓÒÚ¸
3
c
ψ
=
ÔÂðÂÒÂ͇˛ÚÒfl ÔÓ ÔðflÏÓÈ
(ÍÓÓð‰Ë̇Ú̇fl ÎËÌËfl
ρ
). éðÚ˚ ÍðË‚ÓÎËÌÂÈÌÓÈ ÒÙÂð˘ÂÒÍÓÈ ÒËÒ-
ÚÂÏ˚ ÍÓÓð‰ËÌ‡Ú ËÁÓ·ð‡ÊÂÌ˚ ̇ ðËÒ. 1.4.5.
çÂÔÓÒð‰ÒÚ‚ÂÌÌÓ ËÁ ðËÒ. 1.4.3 ÏÓÊÌÓ ÛÒÚ‡ÌÓ‚ËÚ¸ Ò‚flÁ¸ ÏÂʉÛ
‰Â͇ðÚÓ‚˚ÏË Ë ÒÙÂð˘ÂÒÍËÏË ÍÓÓð‰Ë̇ڇÏË:
sin cos
sin sin
cos
x
y
z
ρ
θψ
ρ
θψ
ρθ
=
⎧
⎪
=
⎨
⎪
=
⎩
.
Ç˚˜ËÒÎËÏ ÚÂÔÂð¸ flÍÓ·Ë‡Ì ÔðÂÓ·ð‡ÁÓ‚‡ÌËfl ‰Îfl ÒÙÂð˘ÂÒÍËı ÍÓ-
Óð‰Ë̇Ú:
êËÒ. 1.4.5
x
y
z
0
θ
ρ
к
.л.
θ
к
.л.
ψ
к.л.
ψ
0
ψ
u
ur
0
θ
u
ur
M
0
ρ
u
ur
êËÒ. 1.4.4
x
z
y
0
1
c
ρ
=
x
z
y
0
2
c
θ
=
θ
x
z
y
0
3
c
ψ
=
ψ
‡) ·) ‚)
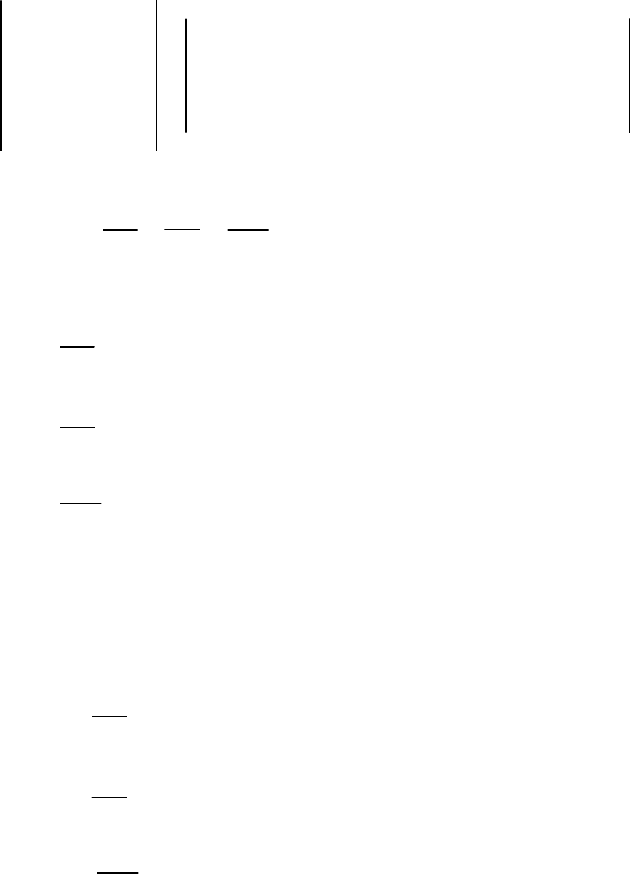
39
2
0
sin cos cos cos sin sin
( , , ) sin sin cos sin sin cos sin .
cos sin
xxx
Jyyy
zzz
ρθψ
ρθψ
ρθψ
θψρθψ ρθψ
ρ
θψ θ ψ ρ θ ψ ρ θ ψ ρ θ
θρθ
′′′
−
′′′
== =
−
′′′
ç‡È‰ÂÏ ÚÂÔÂð¸
r
ρ
∂
∂
,
r
θ
∂
∂
,
r
ψ
∂
∂
‰Îfl ÒÙÂð˘ÂÒÍËı ÍÓÓð‰ËÌ‡Ú ‚ ÒÓÓÚ-
‚ÂÚÒÚ‚ËË Ò ÒÓÓÚÌÓ¯ÂÌËflÏË (4):
r
sin cos i sin sin j cos k
r
cos cos i cos sin
j
sin k
r
sin sin i sin cos j
θψ θψ θ
ρ
ρ
θψρθψρθ
θ
ρθψρθψ
ψ
∂
⎫
=++
⎪
∂
⎪
∂
⎪
=+−
⎬
∂
⎪
∂
⎪
=− +
⎪
∂
⎭
.
Ä ÚÂÔÂð¸ ÌÂÚðÛ‰ÌÓ Ì‡ÔËÒ‡Ú¸ ‚˚ð‡ÊÂÌËfl ‰Îfl ÍÓ˝ÙÙˈËÂÌÚÓ‚ ã‡-
Ï ‚ ÒÙÂð˘ÂÒÍËı ÍÓÓð‰Ë̇ڇı: 1H
ρ
=
, H
θ
ρ
=
Ë sinH
ψ
ρ
θ
= . é˜Â-
‚ˉÌÓ, ˜ÚÓ ÓðÚ˚
0
ρ ,
0
θ ,
0
ψ
Á‡Ô˯ÛÚÒfl Ú‡Í:
0
0
0
r
/ sin cos i sin sin
j
cos k
r
/ cos cos i cos sin
j
sin k
r
/sinicosj
H
H
H
ρ
θ
ψ
θ
ψθψ θ
ρ
θ
ψθψθ
θ
ψψ
ψ
∂
⎫
== + +
⎪
∂
⎪
∂
⎪
== + −
⎬
∂
⎪
∂
⎪
==−+
⎪
∂
⎭
ρ
θ
ψ
.
çÂÚðÛ‰ÌÓ Û·Â‰ËÚ¸Òfl, ˜ÚÓ ÍðË‚ÓÎËÌÂÈ̇fl ÒÙÂð˘ÂÒ͇fl ÒËÒÚÂχ
ÍÓÓð‰ËÌ‡Ú ÓðÚÓ„Ó̇θ̇. ÑÂÈÒÚ‚ËÚÂθÌÓ
00 0 0 0 0
0
⋅
=⋅ =⋅ =ρθ ρψ θψ .
6. ñËÎË̉ð˘ÂÒÍËÂ Ë ÔÓÎflðÌ˚ ÍÓÓð‰Ë̇Ú˚.
ñËÎË̉ð˘ÂÒÍËÏË ÍÓÓð‰Ë̇ڇÏË ÚÓ˜ÍË
M (ðËÒ. 1.4.6) ̇Á˚-
‚‡˛ÚÒfl Ô‡ð‡ÏÂÚð˚:
ρ
– ð‡ÒÒÚÓflÌË ÓÚ ÚÓ˜ÍË
M
‰Ó ÓÒË
Oz
(
0
ρ
≤
<+∞
);
ϕ
– Û„ÓÎ, ÓÚÒ˜ËÚ˚‚‡ÂÏ˚È ÓÚ ÔÎÓÒÍÓÒÚË
xOz
‰Ó ÔÎÓÒÍÓÒÚË, ÔðÓ-
ıÓ‰fl˘ÂÈ ˜ÂðÂÁ ÚÓ˜ÍÛ
M Ë ÓÒ¸ Oz (02
ϕ
π
≤
< );
z – ÍÓÓð‰Ë̇ڇ, ÒÓ‚Ô‡‰‡˛˘‡fl Ò ‰Â͇ðÚÓ‚ÓÈ ÍÓÓð‰Ë̇ÚÓÈ z
(
z−∞ < < +∞ ).
40
é˜Â‚ˉÌÓ, ˜ÚÓ ‚ ˆËÎË̉ð˘ÂÒÍËı ÍÓÓð‰Ë̇ڇı ÍÓÓð‰Ë̇ÚÌ˚ÏË
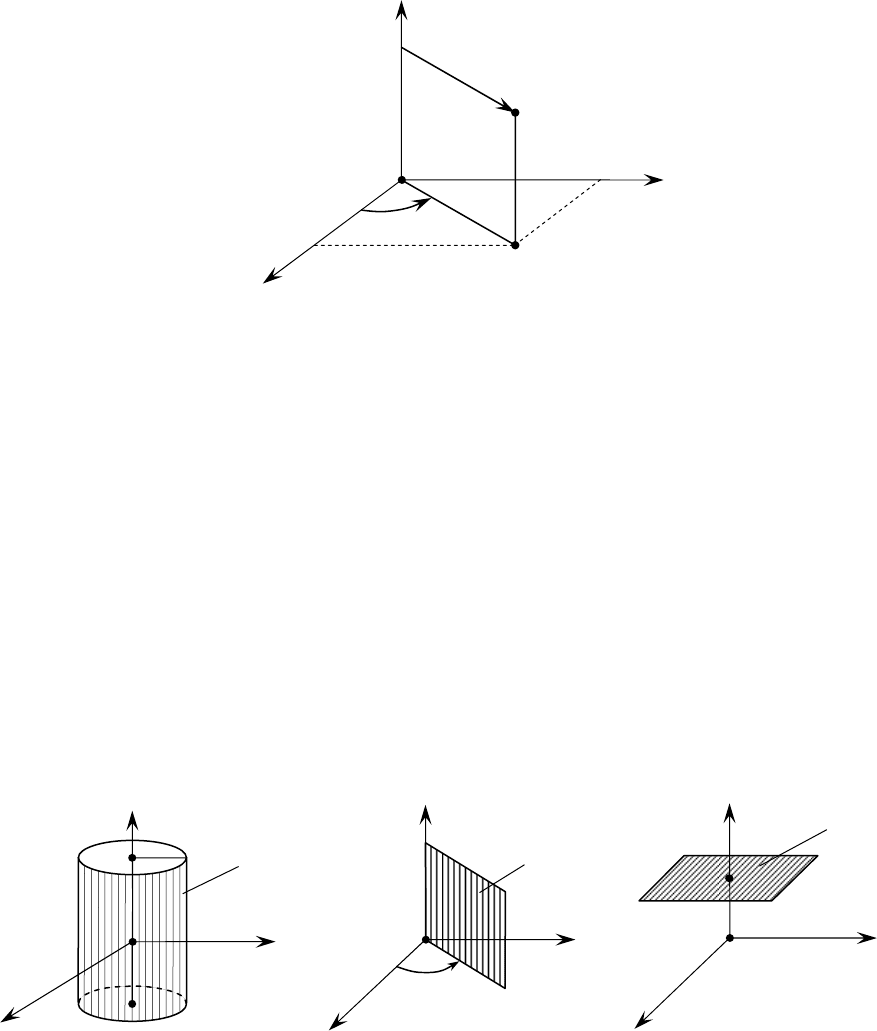
ÔÓ‚ÂðıÌÓÒÚflÏË fl‚Îfl˛ÚÒfl:
1
c
ρ
= – ˆËÎË̉ð˘ÂÒ͇fl ÔÓ‚ÂðıÌÓÒÚ¸, Ó·ð‡ÁÛ˛˘Ë ÍÓÚÓðÓÈ Ô‡-
ð‡ÎÎÂθÌ˚ ÓÒË
Oz , ‡ ̇Ôð‡‚Îfl˛˘ÂÈ ÒÎÛÊËÚ ÓÍðÛÊÌÓÒÚ¸ ‚ ÔÎÓÒÍÓ-
ÒÚË
xOy Ò ˆÂÌÚðÓÏ ‚ ̇˜‡Î ÍÓÓð‰ËÌ‡Ú ð‡‰ËÛÒ‡
1
c
ρ
=
(ðËÒ. 1.4.7
‡);
2
c
ϕ
= – ÔÎÓÒÍÓÒÚ¸, ÔðÓıÓ‰fl˘‡fl ˜ÂðÂÁ ÓÒ¸ Oz Ë Ó·ð‡ÁÛ˛˘‡fl Ò
ÍÓÓð‰Ë̇ÚÌÓÈ ÔÎÓÒÍÓÒÚ¸˛
xOy Û„ÓÎ
ϕ
(ðËÒ. 1.4.7 ·);
3
zc= – ÔÎÓÒÍÓÒÚ¸, Ô‡ð‡ÎÎÂθ̇fl ÍÓÓð‰Ë̇ÚÌÓÈ ÔÎÓÒÍÓÒÚË
xOy
(ðËÒ. 1.4.7 ‚).
äÓÓð‰Ë̇ÚÌ˚ ÔÓ‚ÂðıÌÓÒÚË
1
c
ρ
=
Ë ÔÂðÂÒÂ͇˛ÚÒfl
2
c
ϕ
=
ÔÓ Ôðfl-
ÏÓÈ, Ô‡ð‡ÎÎÂθÌÓÈ ÓÒË
Oz (ÍÓÓð‰Ë̇Ú̇fl ÎËÌËfl z ). äÓÓð‰Ë̇Ú-
Ì˚Â ÔÓ‚ÂðıÌÓÒÚË
1
c
ρ
= Ë
3
zc= ÔÂðÂÒÂ͇˛ÚÒfl ÔÓ ÓÍðÛÊÌÓÒÚË (ÍÓ-
Óð‰Ë̇Ú̇fl ÎËÌËfl
ϕ
). äÓÓð‰Ë̇ÚÌ˚ ÔÓ‚ÂðıÌÓÒÚË
2
c
ϕ
=
Ë
3
zc=
ÔÂðÂÒÂ͇˛ÚÒfl ÔÓ ÔðflÏÓÈ (ÍÓÓð‰Ë̇Ú̇fl ÎËÌËfl
ρ
). éðÚ˚ ˆËÎË̉-
êËÒ. 1.4.6
x
y
z
0
(,,)Mxyz
ρ
u
r
ϕ
x
y
z
êËÒ. 1.4.7
x
z
y
0
2
c
ϕ
=
ϕ
·
)
x
z
y
0
1
c
ρ
=
‡
)
‚
)
x
z
y
0
3
zc=
