Lallart M. Ferroelectrics: Characterization and Modeling
Подождите немного. Документ загружается.

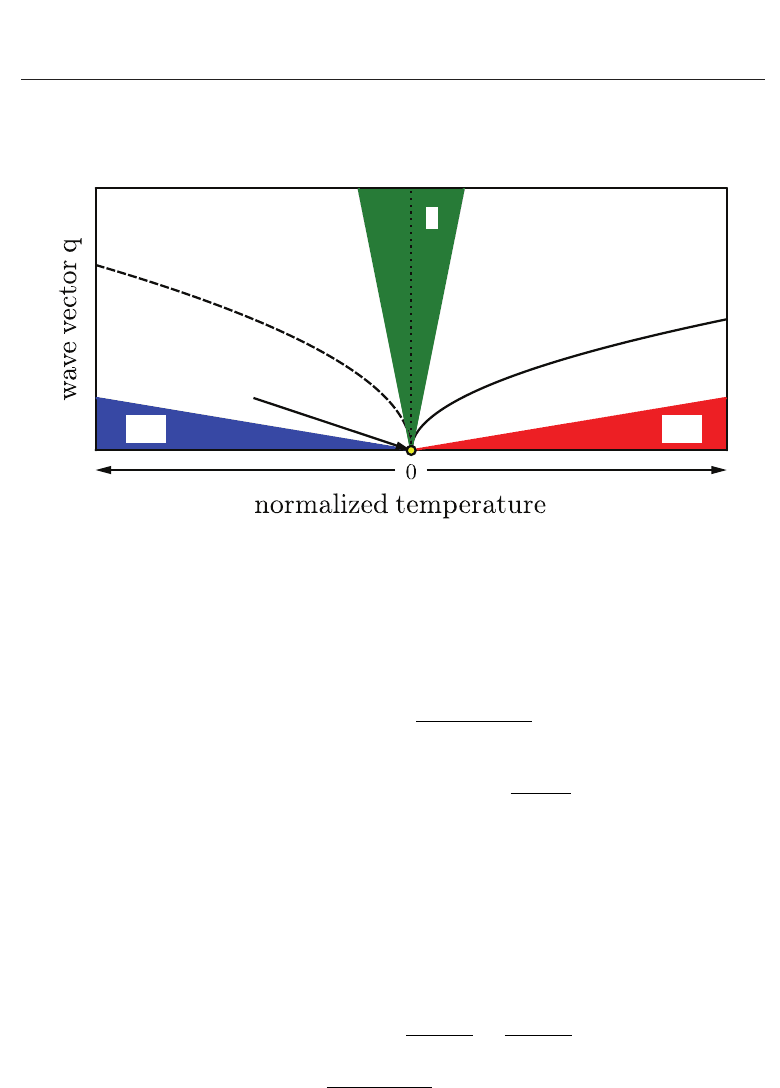
Mesoscopic Modeling of Ferroelectric and Multiferroic Systems 11
scaling functions which depend only on the combination q ξ. The domain of wave vector and
relative distance to the critical temperature τ is due to Hohenberg & Halperin (1977) shown
in Fig. 4. The critical regime denoted as region I is characterized by qξ
>> 1 which is relevant
τ
phase transition
I
II
−
II
+
Fig. 4. Domain of wave vector versus τ =(T − T
c
)/T
c
, I is the critical regime (green), II
±
are
the hydrodynamic regimes above (red) and below T
c
(blue). The bold and the dashed line
indicate the cross-over between the regimes.
for T
≈ T
c
. The two other regimes II
+
and II
−
are the hydrodynamic regimes relevant for
T
> T
c
and T < T
c
, respectively. Our model exhibits propagating modes denoted as ε
l
,
Eq. (22), and ε
h
, Eq. (24). They play the role of the characteristic energy and obey the scaling
form of Eq. (26). So we get in the low temperature phase
ε
l
(
q, T)=qp
x
(T)J
z(1 +(qξ
l
)
−2
). (27)
From here we conclude the dynamical exponent z
c
= 1, the correlation length below the phase
transition ξ
−2
l
= zp
2
z
/p
2
x
and the scaling function f
l
(x) ∝
√
1 + x
−2
. The critical exponents
fulfill the relation ν
= β, which is in accordance with the scaling law z
c
= β/ν. A similar
expression is found above T
c
with the same dynamic exponent, but a different correlation
length ξ
−2
h
= z(p
x
(T
c
) − p
x
(T))/p
x
(T).
3.3 Damping effect
For the complete Eq. (16) with damping we make the same ansatz as in Eq. (18) to find the
complex dispersion relation ω
(
q, T). In the low temperature phase T ≤ T
c
the system reveals
three complex modes
ω
1,2
(
q, T)=±ε
l
(
q, T) − i
Γ
1l
(
q, T)
2τ
1
−i
Γ
2l
(
q, T)
2τ
2
,
ω
3
(
q, T)=−i
(Jzp
z
)
2
J κ(
q)
ε
2
l
(
q, T)τ
1
≡−iω
d
(
q, T) . (28)
459
Mesoscopic Modeling of Ferroelectric and Multiferroic Systems
12 Will-be-set-by-IN-TECH
The spin-wave field
ϕ(
q, t) introduced in Eq. (18) behaves as
ϕ
1,2
(
q, t) ∝ exp
±iε
l
−
Γ
1l
2τ
1
+
Γ
2l
2τ
2
t
, ϕ
3
(
q, T) ∝ exp(−ω
d
(
q, T) t) .
Whereas the modes ω
1,2
describe the propagation of pseudo-spin waves and their damping,
the mode ω
3
= −iω
d
(
q, T) is a pure imaginary one, influenced only by τ
1
. Such a situation
is also known for magnets, see Hohenberg & Halperin (1977) with two complex transverse
modes and one diffusive longitudinal mode. Due to the different physical situation the pure
imaginary mode ω
3
offers here a dispersion relation different to diffusion. The results in
Eq. (28) are valid in the long wave length limit q
1 and in first order in τ
−1
1,2
. In this
approximation the propagating part ε
l
(
q, T) remains unchanged in Eq. (22). Higher order
terms give rise to a slightly changed behavior. The finite life-time of the excitation is related
to the temperature and wave vector dependent damping terms which read
Γ
1l
(
q, T)=
Jκ(
q)Ω
2
z ε
2
l
(
q, T)
q
2
,
Γ
2l
(
q, T)=
ε
2
l
(
q, T)+(Jz p
z
(T))
2
+ Ω
2
Jz
with κ
(
q)=z −q
2
. (29)
At the critical point the damping is continuously as demonstrated in Trimper et al. (2007).
While the life-time in the high temperature phase is only weakly temperature dependent,
it depends on T in the low temperature regime via p
z
which disappears at T
c
according
to p
z
(T) ∝ (−τ)
β
with a critical exponent β ≤ 1/2. The temperature dependence of the
excitation energy and the relevant life-time
(Γ
2l
)
−1
of the soft mode at
q = 0 are depicted in
Trimper et al. (2007). The damping function can be written in scaling form using the results
obtained in subsection (3.2). For simplicity we assume τ
1
τ
2
≡ τ
0
. Defining γ
1l
= Γ
1l
/2τ
o
and γ
2l
= Γ
1l
/2τ
o
. In the long wave length limit it results
2τ
o
γ
1l
Jz
=(qξ
l
)
2
2τ
o
γ
2l
Jzp
2
x
= 1 +
q
2
z
1
+ 2( qξ
l
)
−2
(30)
Whereas the excitation energy ε
l
is dominated by a linear q-term, see Eq. (27), and disappears
for T
→ T
c
at
q = 0, the damping is quadratic in q. In our case the life time remains fixed at T
c
.
Apparently one finds the total damping γ
l
= γ
1l
+ γ
2l
satisfies in the vicinity of the critical
temperature
γ
−1
l
(
q, T
c
) < γ
−1
l
(
q, T ≤ T
c
) .
When the system is approaching the phase transition temperature, the elementary excitation
decays more rapidly for wave vector
q = 0.
The corresponding damping parameters Γ
1h
and Γ
2h
can be also found in the high temperature
limit characterized by p
z
= 0 and p
x
→ 0, compare Fig. 3. The analytical expressions are
presented in Trimper et al. (2007). In that case we obtain ε
h
(
q, T → ∞)=Ω , i.e the mode is
frozen in. A corresponding analysis for the damping shows that the system is overdamped
with ε
h
Γ
1h
.
The analysis can be performed likewise on a microscopic level using Eq. (1), cf. Michael et al.
(2006). In that case a more refined Green’s function technique enables us to calculate both
the excitation energy and its damping. The temperature dependence of both quantities is in
accordance to the present analysis and also in qualitative agreement with experimental results
as shown by Michael et al. (2007).
460
Ferroelectrics - Characterization and Modeling
Mesoscopic Modeling of Ferroelectric and Multiferroic Systems 13
4. Stochastic equation
The model defined by Eq. (16) can be extended by introducing stochastic forces. To that aim
we have two possibilities:
(i ) All the residual degrees of freedom, which are not taken into account so far, will be
incorporated into the model as an additive noise. If this stochastic force is denoted as
η(
x, t) the evolution equation reads now
∂
S
∂t
=
B ×
S −
1
τ
1
B −
1
τ
2
S × (
S ×
B)+
η(
x, t) ,
η
α
(
x, t)η
β
(
x
, t
)
= 2Tδ
αβ
δ(
x −
x
)δ(t − t
) , (31)
where for simplicity a Gaussian white noise is supposed.
(ii ) A second realization is given by assuming that the effective field
B, see Eq. (8), is
extended by a stochastic force, i.e.
B(
x, t) →
B(
x, t)+
η(
x, t). Such a situation leads to
a multiplicative noise and is already discussed for a magnet in Usadel (2006) studying
ferromagnetic resonance, and in Bose & Trimper (2010) including also colored noise.
Here we are interested in the model defined by Eqs. (31). The spin-wave fields obey in the low
temperature phase the relation
∂ϕ
α
(
q, t)
∂t
= W
αβ
(
q) ϕ
β
(
q, t)+η
α
(
q, t) . (32)
Here W isa3
×3 matrix
W
αβ
=
⎛
⎜
⎜
⎝
−
m
z
A
l
τ
2
−A
l
m
z
B
l
q
2
Ωτ
2
A
l
−
Ω
2
+A
2
l
Jzτ
2
−
B
l
q
2
Ω
m
z
Ω
τ
2
Ω −
Jκ(
q)
τ
1
−
B
l
q
2
Jzτ
2
⎞
⎟
⎟
⎠
with the coefficients A
l
= Jzp
z
and B
l
= Ω
2
/z. Eq. (32) is solved by the Green’s function
defined by
G
αβ
(t −t
)=Θ(t − t
)
δϕ
α
(t)
δη
β
(t
)
.
Here Θ
(t) is the Heavyside function. After Fourier transformation the Green’s function is
written in lowest order in τ
−1
1,2
as
G
αβ
(
q, ω)=
g
αβ
(
q , ω)
[ω − ω
1
(
q, T )][ω − ω
2
(
q, T )][iω + ω
d
(
q, T )]
, (33)
where the excitation energies in the low temperature phase ω
1,2
and ω
d
are already introduced
in Eqs. (28). The elements of the matrix g
αβ
(
q , ω) are given by
g
11
= −ω
2
−iω
Ω
+ ε
2
l
Jzτ
2
+
Jκ(
q)
τ
1
+ B
l
q
2
, g
22
= −ω
2
−iω
ε
2
l
Jzτ
2
+
Jκ(
q)
τ
1
,
g
33
= −ω
2
−iω
2A
2
l
+ Ω
2
Jzτ
2
+ A
2
l
, g
12
= A
l
[iω −
Jκ
τ
1
]=−g
21
,
g
23
=
iωB
l
q
2
Ω
= −
B
l
q
2
g
32
Ω
2
, g
13
=
B
l
q
2
Ω
A
l
−
iωp
z
τ
2
=
B
l
q
2
g
31
Ω
2
. (34)
461
Mesoscopic Modeling of Ferroelectric and Multiferroic Systems

14 Will-be-set-by-IN-TECH
The real correlation function is defined conventionally by
ϕ
α
(
q, ω)ϕ
†
(
q, ω)
= C
αβ
(
q, ω)(2π)
d+1
.
Using the solution for ϕ in terms of Green’s function in Eq. (33) and the relation for the
excitation energy ω
∗
1,2
= −ω
2,1
the correlation function reads
C
αβ
(
q, ω)=
2Tc
αβ
(
q, ω)
(ω
2
−ω
2
1
)(ω
2
−ω
2
2
)((ω
2
+ ω
2
d
)
c
αβ
(
q, ω)=g
αμ
(
q, ω)g
∗
μβ
(
q, ω) (35)
The coefficents of the correlation function c
αβ
are obtained from the corresponding expressions
in Eq. (34). A direct calculation shows that the fluctuation-dissipation theorem is fulfilled
C
αβ
(
q, ω)=
2T
ω
G
αβ
(
q, ω) .
In the context of the linear spin-wave approximation the stochastic equations with additive
noise term do not give more information as the conventional equations. The poles of the
Green’s function determine the excitation energy like in the microscopic case. The situation is
different for a multiplicative noise where the effective field
B is supplemented by a stochastic
force. This behavior is discussed for magnets by Bose & Trimper (2010).
5. Multiferroics
As already remarked there is a new class of materials, called multiferroics, see Eerenstein
et al. (2006); Fiebig (2005); Van den Brink & Khomskii (2008), which are classified as materials
possessing at least two ferroic orders such as ferromagnetic and ferroelectric order in a single
phase. For a recent review consult Wang et al. (2009). In this section we present a mesoscopic
model where the ferroelectric properties are described by the Hamiltonian Eq. (3) and the
magnetic part by non-linear sigma model defined in Eq. (4). The total Hamiltonian for such a
multiferroic system reads
H
= H
f
+ H
m
+ H
fm
(36)
The coupling term should be invariant against time reversal symmetry and space inversion.
Due to Mostovoy (2006) we use
H
fm
=
d
d
x λ
αβγδ
S
α
σ
β
∂σ
δ
∂x
γ
, (37)
where the symmetry allowed coupling constant is
λ
αβγδ
= λ
1
αβμ
μγδ
+ λ
2
δ
αβ
δ
γδ
.
In case the magnetization field
σ fulfills ∇·
σ = 0, see Landau & Lifshitz (1935), the coupling
is
H
fm
= λ
1
d
d
x
S · [
σ ×(∇×
σ)] (38)
462
Ferroelectrics - Characterization and Modeling

Mesoscopic Modeling of Ferroelectric and Multiferroic Systems 15
Using the same procedure as before, i.e. defining the effective fields for the magnetic and for
the ferroelectric case, then the equations for the magnetic spin field
σ and the ferroelectric
pseudo-spin field
S are given by the following expressions
∂σ
α
∂t
= K(∇
2
σ)
α
+ λ
1
αβγ
σ
β
σ
μ
∂S
γ
∂x
μ
−S
μ
∂σ
γ
∂x
μ
∂S
α
∂t
=(
B ×
S)
α
+ λ
1
S × (
σ ×∇×
σ)
α
. (39)
The internal field for the ferroelectric subsystem is defined in Eq. (9). Now let us discuss the
excitation energies for the magnetic and the ferroelectric system which are coupled mutually
due to the multiferroic effect. To this aim we set according to Eq. (18)
S(
x, t)=
p(
x)+
ϕ(
x, t) ,
σ(
x, t)=
m(
x)+
Φ(
x, t) .
For simplicity we consider excitations around a homogeneous ground state, i.e
p =(p
x
,0,p
z
)
and
m =(0, 0, m
z
). The magnetization
m points in the z-direction. Here we consider
the experimentally realized situation, compare the review article by Wang et al. (2009),
that lowering the temperature the system undergoes firstly at T
c
a phase transition into a
ferroelectric phase characterized by p
z
= 0,p
x
= Ω/(Jz) as well as m
z
= 0. This phase is
observable in the temperature regime T
m
≤ T < T
c
, where T
m
is the magnetic phase transition
temperature. A further reducing of the temperature leads at T
= T
m
< T
c
to a transition into
the magnetic phase, characterized by m
z
= 0. In the low temperature regime one observes the
multiferroic phase with m
z
= 0, p
z
= 0 and p
x
= Ω/Jz. In this regime the excitation energy
offers a dispersion relation which depends on the parameters of the ferroelectric subsystem
( J, ω), the coupling strength of the magnetic system K as well as the mutual coupling constant
λ
1
between both systems. A tedious but straightforward calculation shows that the excitation
energy of the ferroelectric system ε
l
(
q, T) remains unchanged in first order expansion with
respect to the coupling λ
1
, i.e. in the interval T
m
< T ≤ T
c
the system reveals a soft mode
behavior characterized by the dispersion relation presented in Eq. (18). In the low temperature
phase T
< T
m
we get in lowest order in λ
1
an excitation energy of the multiferroic system in
the following form
ε
2
fm
(
q, T)=(Km
z
(T)q)
2
( q
2
x
+(q
y
+ Q)
2
+ q
2
z
− Q
2
. (40)
Here the parameter Q is defined by
Q
=
λ
1
Ω
2JKz
.
This parameter reflects the influence of the ferroelectricity in the multiferroic phase. In
absence of a multiferroic coupling the dispersion relation yields the well known Goldstone
mode of the magnetic system ε
m
= Km
z
q
2
. The multiferroic mode ε
fm
remains a Goldstone
mode, i. e. ε
fm
(
q = 0)=0, because at the magnetic transition a continuous symmetry is
broken. The wave vector Q indicates (probably) the presence of spiral structures, compare
Tokura & Seki (2010). Notice that we have considered only excitations with respect to the
homogeneous ground state characterized by
p = const. The result is altered in case one
studies an inhomogeneous static state given by Eq. (19) for instance. This point deserves
further studies.
463
Mesoscopic Modeling of Ferroelectric and Multiferroic Systems

16 Will-be-set-by-IN-TECH
6. Conclusions
In this chapter we have discussed a mesoscopic modeling of ferroelectric materials. There
exists two limiting cases denoted as displacive and order-disorder ones. The last category
is often discussed in terms of an Ising model in a transverse field. Such a quantum model
can be studied using different techniques, especially Green’s function methods. Otherwise
ferroelectric systems offer a phase transition at finite temperatures. In this region the quantum
effects are not relevant and therefore, a mesoscopic description should be adequate. The
mesoscopic limit of the underlying quantum model is constructed in such a manner that the
evolution equations coincides, namely those based on the Heisenberg equation of motion and
on the Poisson bracket relations, respectively. The main effort in this region came from the
analysis of magnetic materials. Motivated by several theoretical activities in that field, we
have studied the basic model for describing the order-disorder transition in ferroelectrics.
To that aim we have brought forward the concept of mesoscopic evolution equations with
damping terms to one of the standard models for ferroelectricity. In doing so we followed
our paper, see Trimper et al. (2007), which is modified and extended accordingly. Whereas
the previous discussion was primarily focused on isotropic magnetic systems, we are able
to derive the mesoscopic evolution equation for a ferroelectric system under quite general
conditions as the behavior of the spin moments, a self-organized effective field and its
behavior under time reversal symmetry as well as the underlying Lie group properties of the
moments. In particular, we have demonstrated that the form of the damping terms is rather
universal, although the realization of the effective field in ferroelectric systems is distinct from
that of the ferromagnet ones. The reason consists of the different symmetry of the ferroelectric
system. While the classical Heisenberg model reflects the isotropic symmetry, the Ising model
in a transverse field is anisotropic. The differences are clearly indicated. Consequently
the differences lead to a totally different dynamic behavior which is observed in both the
reversible propagating part and its damping. Thus the ferroelectric mode becomes a massive
one and the life-time of the elementary excitation offers another temperature dependence.
In terms of a multi-scale approach the relevant incoming static quantities as the polarization
are calculated using the microscopic model. Our approach allows the investigation of both
the low and the high temperature phase. They are discussed within dynamic scaling theory.
As a further step we are interested in systems where magnetic and polarization behavior is
coupled leading to a new class of systems known as multiferroicity reviewed recently by
Wang et al. (2009). Such systems are characterized by the occurrence of spiral structures
manifested in an inhomogeneous ground state as shown in Eq. (19). In the quantum model
this phenomena can be described by spin operators without fixed quantization direction, as
studied by Michael & Trimper (2011). In this chapter we studied a simple model allowing a
sequence of phases, namely for T
> T
c
the system is paraelectric as well as paramagnetic.
Reducing the temperature the system offers a phase transition at T
c
into a ferroelectric but
paramagnetic phase. When the temperature is lowered further there is at T
m
a transition into
the magnetic phase which is due to the multiferroic coupling simultaneously characterized
by the parameters of the ferroelectric and the magnetic system. The multiferroic dispersion
relation suggests the occurrence of incommensurable structures which can be also interpreted
as spiral structure. A related more detailed approach using the mesoscopic formulation is
under progress.
464
Ferroelectrics - Characterization and Modeling

Mesoscopic Modeling of Ferroelectric and Multiferroic Systems 17
7. References
Blinc, R. & Zeks, B. (1972). Dynamics of order-disorder-type ferroelectrics and
anti-ferroelectrics, Adv. Phys. 21: 693.
Blinc, R. & Zeks, B. (1974). Soft modes in ferroelectrics and antiferroelectrics, North-Holland,
Amsterdam.
Bose, T. & Trimper, S. (2010). Correlation effects in the stochastic Landau-Lifshitz-Gilbert
equation, Phys. Rev. B 81(10): 104413.
Bose, T. & Trimper, S. (2011). Lagrangian formulation of a dissipative magnetic system on a
mesoscopic scale, Euro. Phys. Lett. submitted .
Cano, A. & Levanyuk, A. P. (2004). Low-temperature structural phase transitions: Phonon-like
and relaxation order-parameter dynamics, Phys. Rev. B 70: 064104.
de Gennes, P. G. (1963). Collective motions of hydrogen bonds, Solid State Communications
1: 37.
Denisov, S. I., Lyutyy, T. V. & Hänggi, P. (2006). Magnetization of nanoparticle systems in a
rotating magnetic field, Phys. Rev. Lett. 97: 227202.
Duine, R. A., Núñez, A. S. & MacDonald, A. H. (2007). Thermally assisted current-driven
domain-wall motion, Phys. Rev. Lett. 98: 056605.
Eerenstein, W., Mathur, N. D. & Scot, t, J. (2006). Multiferroic and magnetoelectric materials,
Nature 442: 759.
Elliot, R. J. & Wood, C. (1971). The Ising model with a transverse field. i. high temperature
expansion, J.Phys. C: Solid State Phys. 4: 2359.
Fiebig, M. (2005). Revival of the magnetoelectric effect, J.Phys.D: Appl.Phys. 38: R123.
Gaunt, D. S. & Domb, C. (1970). Equation of state of the Ising model near the critical point, J.
Phys. C: Solid State Phys. 3: 1442.
Gilbert, T. L. (2004). A phenomenological theory of damping in ferromagnetic materials, IEEE
Trans. Magn 40: 3343.
He, P.-B. & Liu, W. M. (2005). Nonlinear magnetization dynamics in a ferromagnetic nanowire
with spin current, Phys. Rev. B 72: 064410.
Hohenberg, P. C. & Halperin, B. I. (1977). Theory of dynamic critical phenomena, Rev. Mod.
Phys. 49: 435–479.
Kühnel, A., Wendt, S. & Wesselinowa, J. (1977). Dynamic behaviour of the Ising model in a
transverse field, physica status solidi (b) 84: 653.
Landau, L. D. & Lifshitz, E. M. (1935). On the theory of the dispersion of magnetic
permeability in ferromagnetic bodies, Zeitschr. d. Sowjet. 8: 153.
Landau, L. D., Lifshitz, E. M. & Pitaevski, L. P. (1980). Statistical Physics, Part 2, Pergamon,
Oxford.
Lines, M. E. & Glass, A. (2004). Principles and Applications of Ferroelectrics and Related Materials,
Clarendon Press, Oxford.
Mazenko, G. F. (2003). Fluctuations, order, and defects, John Wiley & Sons. Inc Hoboken, New
jersey.
Michael, T. & Trimper, S. (2011). The excitation spectrum of multiferroics at finite
temperatures, Phys. Rev. B accepted .
Michael, T., Trimper, S. & Wesselinowa, J. M. (2006). Size and doping effects on the coercive
field of ferroelectric nanoparticles: A microscopic model, Phys. Rev. B 74: 214113.
Michael, T., Trimper, S. & Wesselinowa, J. M. (2007). Size effects on static and dynamic
properties of ferroelectric nanoparticles, Phys. Rev. B 76: 094107.
Mostovoy, M. (2006). Ferroelectricity in spiral magnets, Phys. Rev. Lett. 96: 067601.
465
Mesoscopic Modeling of Ferroelectric and Multiferroic Systems

18 Will-be-set-by-IN-TECH
Ohe, J.-i. & Kramer, B. (2006). Dynamics of a domain wall and spin-wave excitations driven
by a mesoscopic current, Phys. Rev. Lett. 96: 027204.
Pfeuty, P. & Elliot, R. J. (1971). The Ising model with a transverse field. ii. ground state
properties, J. Phys. C: Solid State Phys. 4: 2370.
Stinchcombe, R. B. (1971). Ising model in a transverse field. ii. spectral functions and damping,
J. Phys. C: Solid State Phys. 6: 2484, 2507.
Stinchcombe, R. B. (1973). Ising model in a transverse field, J. Phys. C: Solid State Phys. 6: 2459.
Strukov, B. A. & Levnyuk, A. P. (1998). Ferroelectric Phenomena in Crystals, Springer, Berlin.
Tokura, Y. & Seki, S. (2010). Multiferroics with spiral spin order, Adv. Mater. 22: 1554.
Trimper, S., Michael, T. & Wesselinowa, J. M. (2007). Ferroelectric soft modes and Gilbert
damping, Phys. Rev. B 76: 094108.
Tserkovnyak, Y., Brataas, A., Bauer, G. E. W. & Halperin, B. I. (2005). Nonlocal magnetization
dynamics in ferromagnetic heterostructures, Rev. Mod. Phys. 77: 1375–1421.
Usadel, K. D. (2006). Temperature-dependent dynamical behavior of nanoparticles as probed
by ferromagnetic resonance using Landau-Lifshitz-Gilbert dynamics in a classical
spin model, Phys. Rev. B 73: 212405.
Van den Brink, J. & Khomskii, D. (2008). Multiferroicity due to charge ordering, J. Phys.:
Condens. Matter 20 (2008) 434217 (12pp) 20: 434217.
Wang, K. F., Liu, J. M. & Ren, Z. F. (2009). Multiferroicity: the coupling between magnetic and
polarization order, Adv. Phys. 58: 321.
Wang, Y.-L. & Cooper, B. R. (1968). Collective excitations and magnetic ordering in materials
with singlet crystal-field ground state, Phys. Rev. 172: 539–551.
Wesselinowa, J. M. (1984). Damping of the transverse and longitudional excitations of the
IIsng model in a transverse field, physica status solidi (b) 121: 317.
Wesselinowa, J. M. & Kovachev, S. (2007). Hardening and softening of soft phonon modes in
ferroelectric thin films, Phys. Rev. B 75: 045411.
Wesselinowa, J. M., Michael, T. & Trimper, S. (2010). Handbook of Nanophysics Vol.4, Taylor &
Francis, London, Editor: Klaus Sattler.
Wesselinowa, J. M., Trimper, S. & Zabrocki, K. (2005). Impact of layer defects in ferroelectric
thin films, J. Phys.: Cond. Mat 17: 4687.
466
Ferroelectrics - Characterization and Modeling

24
A General Conductivity Expression
for Space-Charge-Limited Conduction in
Ferroelectrics and Other Solid Dielectrics
1
Ho-Kei Chan
1,2
1
School of Physics, Trinity College Dublin, College Green, Dublin 2,
2
Department of Applied Physics, Hong Kong Polytechnic University, Kowloon,
1
Ireland
2
Hong Kong, China
1. Introduction
For a current density J and an applied voltage V, the experimentally observable Mott-
Gurney law J ~ V
2
(Carbone et al., 2005; Coelho, 1979; Laha & Krupanidhi, 2002; Pope &
Swemberg, 1998; Suh et al., 2000) for steady-state trap-free space-charge-limited conduction
(SCLC) inside a plane-parallel dielectric capacitor is derived from three independent
assumptions - (i) the presence of a single free-carrier type (i.e. injection of only p-type or n-
type free charge-carriers into the dielectric), (ii) the absence of an intrinsic (Ohmic)
conductivity, and (iii) the existence of a constant dielectric permittivity ε (i.e. the material
being a linear dielectric). Due to the limited applicability of the Mott-Gurney law, there has
been the need to derive a more general SCLC formula that applies to cases (i) with the
simultaneous presence of p-type and n-type free charge-carriers, (ii) with the presence of a
small but finite intrinsic conductivity σ
in
, as well as (iii) with any possible field dependence
of the dielectric permittivity ε. In 2003, while we were searching for a theoretical explanation
to the well-known experimental observation of polarization offsets (Schubring et al., 1992) in
compositionally graded ferroelectric films, we employed the law of mass action to derive a
general local conductivity expression for double-carrier-type SCLC in solid dielectrics and
showed numerically that SCLC is a possible origin of the observation of polarization offsets
in those graded ferroelectric films (Chan et al., 2004). In those graded films, there exist
gradients of electric displacements and therefore, according to Gauss’ law, a corresponding
presence of free space-charge. The local electrical conductivity is influenced, or even limited,
by the presence of free space-charge and consequently becomes non-Ohmic. An important
conclusion from this general local conductivity expression is the necessary dominance of a
single free-carrier type at the limit of zero intrinsic conductivity, which links two of the three
independent assumptions in the original derivation of the Mott-Gurney law. In a later study
(Zhou et al., 2005a), we have employed this new conductivity expression to understand the
origin of imprint effect in homogeneous ferroelectric films. In this Book Chapter, we will (i)
review the original derivation of the Mott-Gurney law (Coelho, 1979; Pope & Swemberg,
1
e-mail: epkeiyeah@yahoo.com.hk
Ferroelectrics - Characterization and Modeling
468
1998), (ii) review the original problem of polarization offsets in compositionally graded
ferroelectric films (Schubring et al., 1992) and explain why such a new local conductivity
expression was needed in our theoretical investigation, (iii) review our original derivation of
this general local conductivity expression (Chan et al., 2004), (iv) review our study on the
limiting case of zero intrinsic conductivity (Chan et al., 2007; Zhou et al., 2005a), (v) supply
the derivation of a general expression, via the mass-action approximation, for the
corresponding local diffusion-current density (Chan, unpublished), which incorporates the
Einstein relations and takes into account the possible presence of a temperature gradient,
(vi) present an alternative derivation of this local conductivity expression (Chan,
unpublished) with a detailed theoretical justification of the mass-action approximation, and
(vii) discuss, in the concluding section, possible future work as to a better understanding of
the mechanism of charge flow in a compositionally graded ferroelectric film as well as of the
scope of applicability of the general local conductivity expression.
2. Derivation of the Mott-Gurney law
Space-charge-limited conduction (SCLC) in a solid dielectric occurs when free charge-
carriers are injected into the dielectric sample at relatively large electric fields (Carbone et
al., 2005; Coelho, 1979; Laha & Krupanidhi, 2002; Pope & Swemberg, 1998; Suh et al., 2000).
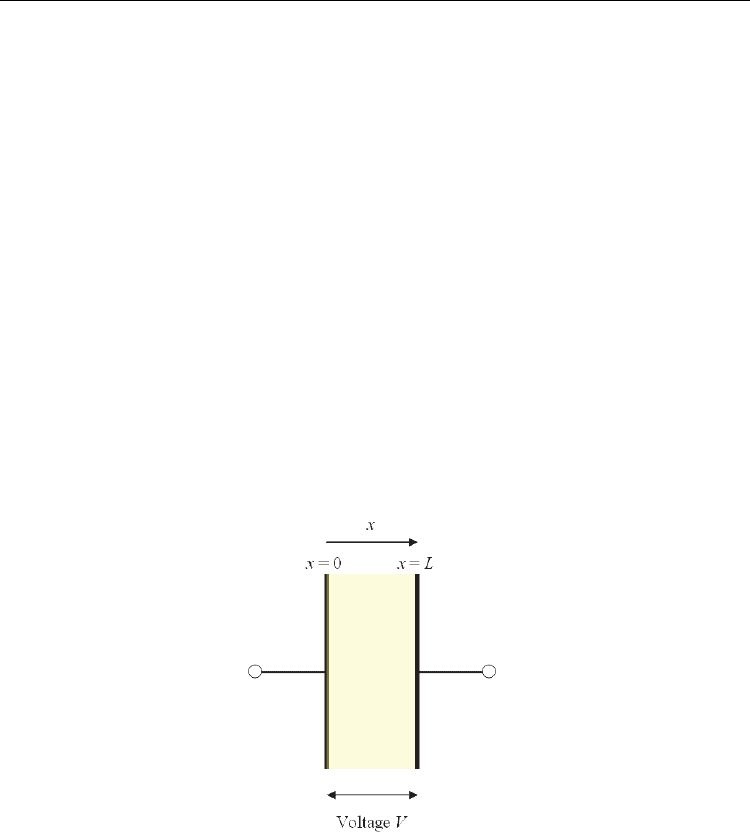
For the case of SCLC in a trap-free plane-parallel dielectric capacitor (Fig. 1), the current
density J and the applied voltage V follow a scaling relation
Fig. 1. Schematic diagram of a plane-parallel dielectric capacitor. V is the applied voltage,
and x is the position from the electrode where the electric current flows into the dielectric
sample. The positive direction of x is the flow direction of the electric current.
2
J~V
(1)
which can be observed experimentally (Carbone et al., 2005; Laha & Krupanidhi, 2002; Suh
et al., 2000), and can be derived theoretically (Coelho, 1979) as follows: Consider the case of
SCLC by only p-type free charge-carriers, and let this case be denoted by a subscript p in
each of the quantities involved. Let the charge mobility μ
p
> 0 and the dielectric permittivity
