Lalanne C. Mechanical Vibrations and Shocks: Mechanical Shock Volume II
Подождите немного. Документ загружается.

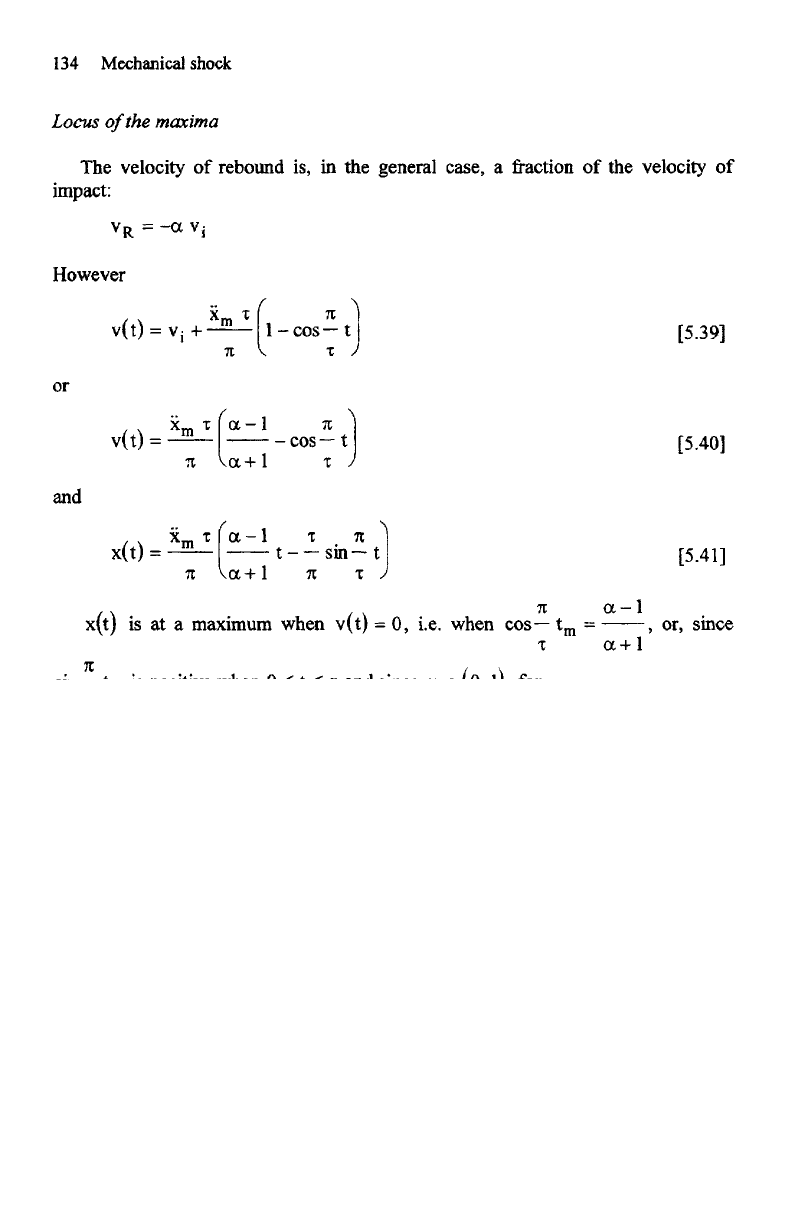
134
Mechanical shock
Locus
of
the
maxima
The
velocity
of
rebound
is, in the
general case,
a fraction of the
velocity
of
impact:
However
or
and
x(t)
is at a
maximum when v(t)
= 0,
i.e. when
or,
since
is
positive
when
0 < t < t and
since
for
Thus
The
locus
of
maxima, given
by the
parametric representation
t
m
(a),
x
m
(a),
can
be
expressed
according
to a
relation
x
m
(t
m
)
while
eliminating
a
between
the two
relations:

Kinematics
of
simple shocks
135
The
locus
of the
maxima
is an arc of the
curve representative
of
this function
in
T
the
interval
— < t
m
< T .
2
Table 5.5.
Summary
of
the
conditions
for the
realization
of
a
half-sine
shock
Impulse
Impact without
rebound
Impact with
perfect rebound
Impact
with
rebound
to 50%
of
the
initial
velocity
136
Mechanical shock
5.3.
Versed-sine
pulse
5.3.1.
Definition
The
versed-sine*
(or
haversine**
)
shape consists
of an arc of
sinusoid ranging
between
two
successive minima.
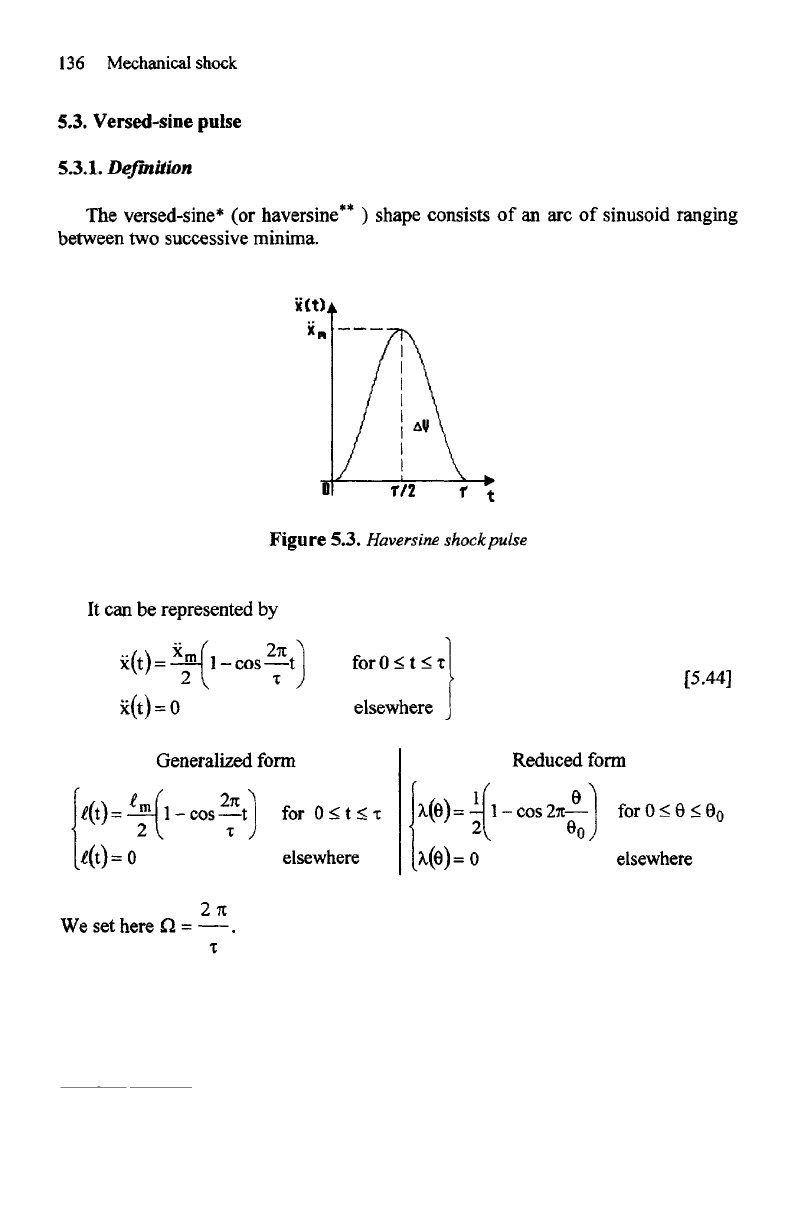
Figure
5.3.
Haversine
shock pulse
It
can be
represented
by
elsewhere
for
Generalized
form
Reduced
form
for
for
elsewhere
elsewhere
We
set
here
One
minus Cosine
One
half
of one
minus Cosine

a
General
expressions
Kinematics
of
simple
shocks
137
(it
is
supposed that x(o)
= 0).
Impulse
mode
v
Table
5.6.
Velocity
and
displacement
for
carrying
out a
versed-sine
shock
pulse
Impact
without
rebound
Impact with
perfect
rebound
Impact
with
50%
rebound
Velocity
Displacement

138
Mechanical shock
(by
preserving
the
notation
V
R
= -a
vi). Table
5.6
gives
the
expressions
for the
velocity
and the
displacement using
the
same assumptions
as for the
half-sine pulse.
Table 5.7.
Summary
of
the
conditions
for the
realization
of
a
haversine shock pulse
Impulse
Impact without
rebound
Impact
with
perfect rebound
Impact with
rebound
to 50%
of
the
initial
velocity
Kinematics
of
simple
shocks
139
5.4. Rectangular pulse
5.4.1.
Definition
Generalized
form
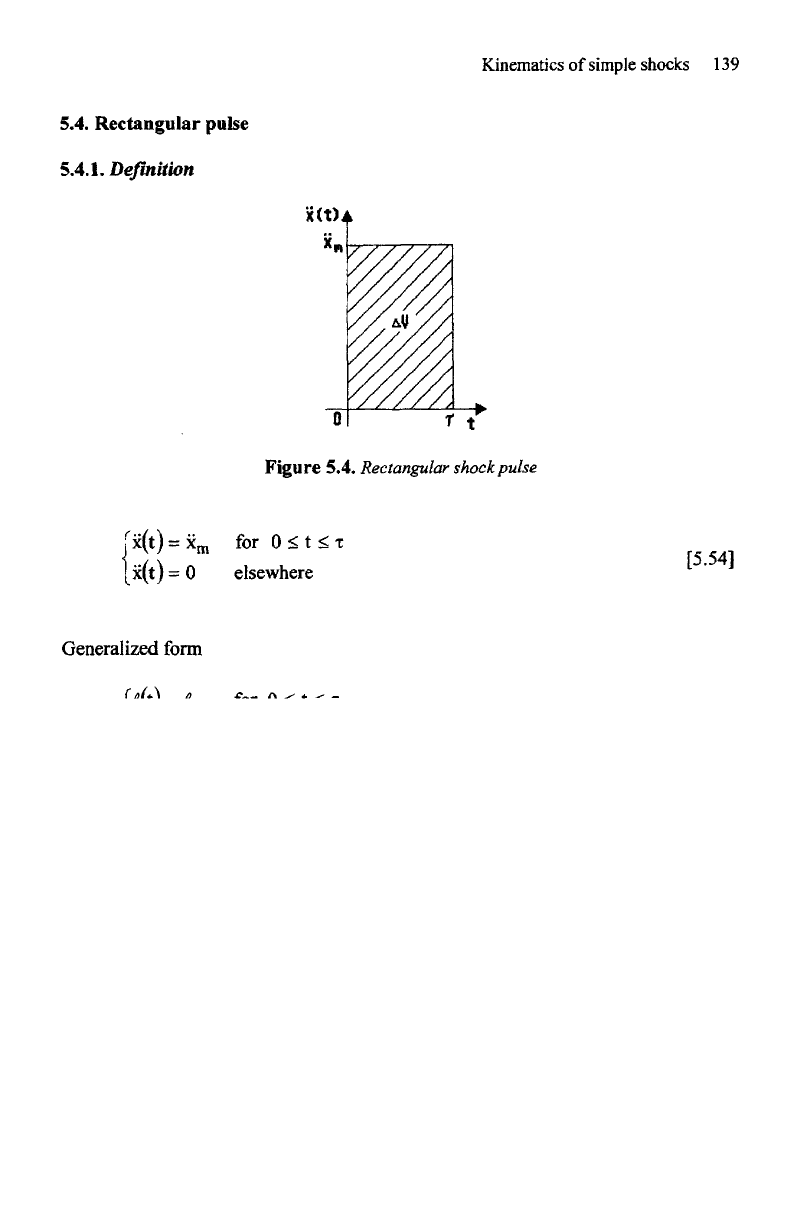
Figure
5.4. Rectangular shock pulse
for
elsewhere
for
elsewhere
Reduced
form
for
elsewhere
5.4.2. Shock motion
study
General
expressions

140
Mechanical shock
Impulse
Impact
Table
5.8.
Velocity
and
displacement:
rectangular
shock
pulse
Impact without
rebound
Impact with
perfect
rebound
Impact with
50%
rebound
Velocity
Displacement

Kinematics
of
simple
shocks
141
Table
5.9. Summary
of
the
conditions
for the
realization
of
a
rectangular shock pulse
Impulse
Impact without
rebound
Impact with
perfect
rebound
Impact with
rebound
to 50%
of
the
initial
velocity
142
Mechanical shock
5.5. Terminal peak
saw
tooth pulse
5.5.1.
Definition
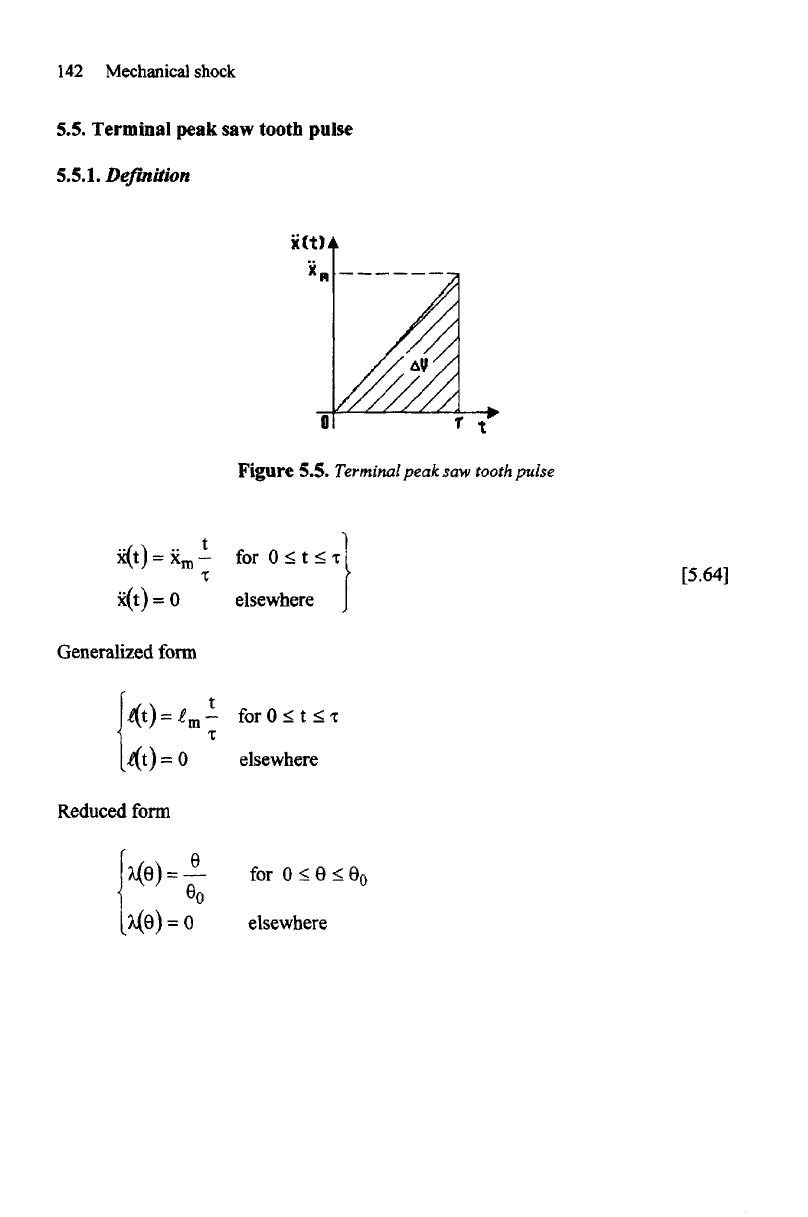
Figure 5.5.
Terminal
peak
saw
tooth pulse
for
elsewhere
Generalized
form
for
elsewhere
Reduced
form
for
elsewhere

Kinematics
of
simple
shocks
143
5.5.2.
Shock
motion
study
General expressions
Impulse Impact
Table
5.1
Impact without
rebound
Impact with
perfect
rebound
Impact with
50%
rebound
10.
Velocity
and
displacement
to
carry
out a TPS
shock
pulse
Velocity
Displacement
