Лахтин Ю.М., Леонтьева В.П. Материаловедение

Подождите немного. Документ загружается.

взаимодействия и предположения, что два ряда атомов

одновременно смещаются относительно друг друга под действием

напряжения сдвига. Исходя из кристаллического строения и

межатомных сил, можно ориентировочно определить

теоретическую прочность металла по следующей формуле: τ

теор

G/(2π), где G — модуль сдвига

(коэффициент пропорциональности

между ка-cательным напряжением τ и

относительным сдвигом γ (τ

= Gγ)).

Теоретическое значение прочности, рассчитываемое по

указанной формуле, в 100—1000 раз больше технической

прочности. Это связано c

дефектами в кристаллическом

строении, и прежде всего c

существованием дислокаций.

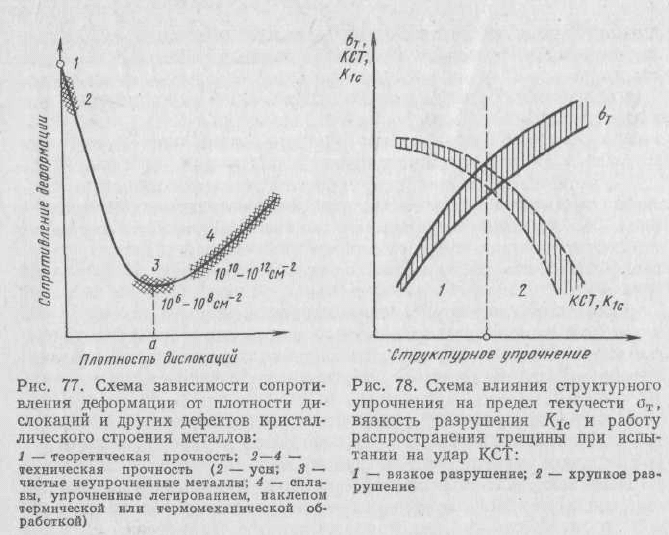
Прочность металлов не являетcя линейной функцией плотности

дислокаций (рис. 77).

Как видно из рис. 77, минимальная прочность определяется

некоторой критической плотностью дислокаций а, приближенно

составляющей 10

—10

см

-2

. Эта величина относится к

отожженным металлам. Величина σ

0,2

отожженных металлов

составляет 10

-5

—10

-4

Повышение прочности достигается: созданием металлов и

сплавов с бездефектной структурой; повышением плотности

дефектов (в том числе дислокаций), затрудняющих движение

дислокаций.

Если плотность дислокаций (количество дефектов) меньше

величины а (рис. 77), сопротивление деформации резко

увеличивается и прочность быстро приближается к

теоретической.

В настоящее время удалось получить кристаллы, практически

не содержащие дислокаций. Эти нитевидные кристаллы

небольших размеров (длиной 2—10 мм и толщиной 0,5—2,0 мкм),

называемые «усами», обладают прочностью, близкой к

теоретической. Так, предел прочности нитевидных кристаллов

железа составляет 13 000 МПа, меди 3000 МПа и цинка 2250

МПа, по сравнению β пределом прочности технического железа

300 МПа, меди 260 МПа

и цинка 180 МПа.

Увеличение размеров усов сопровождается резким снижением

прочности, что ограничивает их использование. Они нашли

применение для армирования волокнистых композиционных

материалов (см. в. 422), в микроэлектронике, для микроподвесок и

микрорастяжек и т. д.

При возрастании количества дефектов свыше 10

—10

см

-2

(см. риз. 77) происходит упрочнение металла вследствие

взаимодействия дислокаций и торможения их движения. Связь

между пределом текучести σ

и плотностью дислокаций ρ может

быть описана уравнением

= σ

+ αGb √p,

По более точным расчетам для металлов с ГЦК решеткой τ

теор

= 0,039G и для

металлов с ОЦК решеткой σ

теор

= 0,11G. Модуль сдвига для Fe равен 77 000 МПа, для

Си — 44 000 МПа, для А1 — 27 000 МПа.

111

где

—

— напряжение сдвига до упрочнения (после отжига); b

вектор Бюргерса; α — коэффициент, зависящий от природы

металла, его кристаллической решетки и структуры. Плотность

дислокаций не должна превышать 10

—10

см

-2

. При большей

плотности дислокаций образуются трещины.

Сопротивление пластической деформации (σ

, σ

) тем выше, чем

меньше подвижность дислокации, чем больше препятствий (барьеров)

на их пути. Пластичность (δ, ψ) и вязкость (KCU), наоборот, тем

выше, чем легче осуществляется движение дислокации. Следует

иметь в виду, что помимо вязкого разрушения, являющегося

результатом большого числа пластических сдвигов за счет движения

дислокаций по различным плоскостям скольжения, возможно

хрупкое разрушение в результате зарождения и прогрессирующего

развития трещины.

На рис. 78 показано влияние структурного упрочнения (создание

структурных барьеров для движения дислокаций) на предел

текучести σ

, трещиностойкость K

1с

и работу распространения

трещины КСТ. С увеличением барьеров для движения дислокаций

предел текучести возрастает, а трещиностойкость К

1с

и работа

распространения трещины КСТ уменьшаются. В области 1

(рис. 78) надежность против внезапных хрупких разрушений высокая,

так как случайные перегрузки будут сниматься пластической

деформацией в устье трещины в связи с низким пределом текучести

и высоким значением вязкости разрушения K

1с

112

Область 2 (рис. 78) соответствует высокому значению σ

низкому значению K

1с

металл может разрушаться хрупко при

малых нагрузках. Поэтому во многих случах следует применять

материал с меньшим σ

, что несколько увеличит массу

конструкций, но значительно повысит сопротивление хрупкому

разрушению.

Для получения высокого комплекса механических свойств

(высокой конструктивной прочности), исключения возможности

хрупкого разрушения нужно, чтобы барьеры, тормозящие

движение дислокаций, позволяли при определенном напряжении

прорываться через них дислокациям («полупроницаемые»

барьеры).

Рассмотрим с этих позиций основные механизмы упрочнения:

деформационное, твердорастворное, образование гетерогенных

структур (дисперсионное упрочнение), различного рода границ

и оценим их роль в охрупчивании металлов.

Деформационное упрочнение (наклеп) рассмотрено выше.

Беспорядочно расположенные дислокации («лес дислокаций») в

деформированном металле вызывает сильное повышение

прочности (σ

= 10

-3

÷10

-2

G при ρ = 10

÷10

см

-2

), но одновременно резко

снижается сопротивление хрупкому разрушению. Следовательно,

деформационное упрочнение не обеспечивает высокой

конструктивной прочности. Оно нашло применение для

упрочнения сплавов твердых растворов.

При образовании твердых растворов σ

, σ

и НВ повышаются

(твердорастворное упрочнение). В неупорядоченном твердом

растворе возникающие вокруг атомов растворенного элемента поля

упругих напряжений затрудняют скольжение дислокаций.

Степень торможения дислокаций в твердом растворе определяется

фактором размерного несоответствия атомов растворителя и

растворенного элемента, разностью модулей упругости и возрастает

пропорционально концентрации.

В первом приближении упрочнение при образовании твердого

раствора может быть определено по формуле, полученной Моттом

и Набарро:

= GΕ

где G — модуль сдвига, МПа; ε —параметр, зависящий от

различия размеров атомов растворенного компонента r и

растворителя r

(ε = (r — r

)/r

); С — атомная концентрация

растворенного компонента.

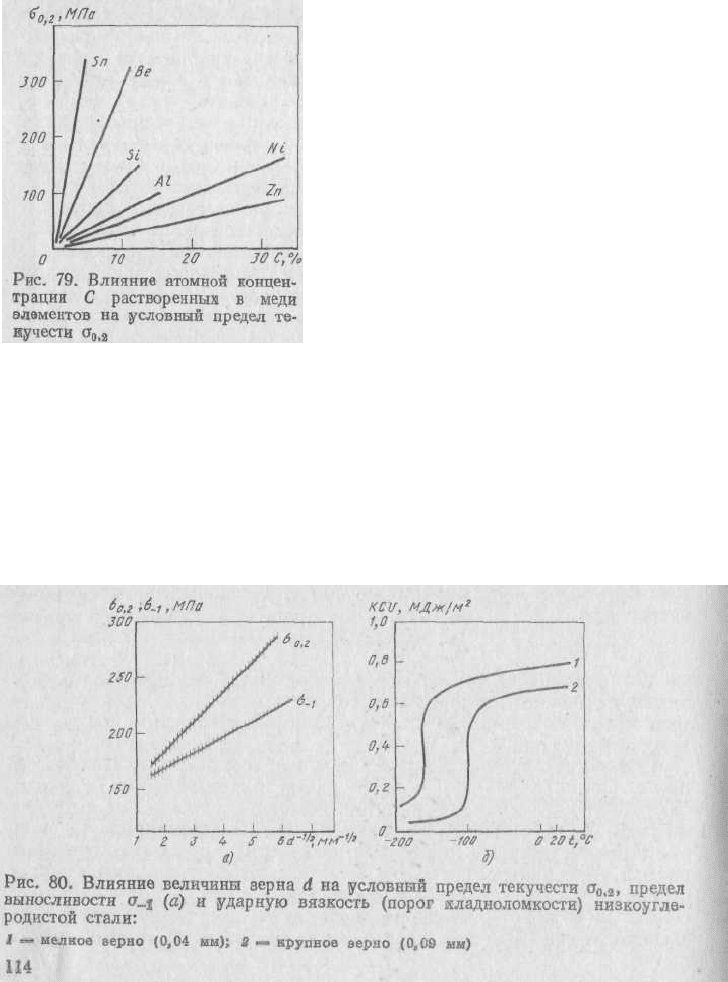
Повышение прочности (рис. 79) в твердом растворе замещения

прямо пропорционально концентрации растворенного элемента

(до 10—30 %). Однако абсолютная величина упрочнения зависит

от вида растворимого компонента (рис 79). Величина K

при

образовании твердых растворов снижается. В случае твердого

раствора внедрения прочность во много раз больше, чем при

образовании твердого раствора замещения при той же

концентрации. Очень затрудняют движение дислокации, а

следовательно, повышают прочность атмосферы Коттрелла, даже

при малом содер-

113

жании второго компонента внедрения.

Примеси внедрения сильно понижают

трещиностойкость K

, работу

распространения трещины КСТ и

повышают порог хладноломкости.

Очистка хладноломких металлов (Fe,

Cr,

MO, W и др.) от примесей внедрения

(О

, N

, H

) повышает работу

распространения трещины, вязкость

разрушения K

и понижает порог

хладноломкости.

Основная причина охрупчива-ния

металла в присутствии примесей

внедрения — малая подвижность

дислокации. Это вызвано,

с одной

стороны, повышенным сопротивлением

решетки раствора внедрения скольжению

дислокаций и, с

другой стороны, закреплением дислокаций атмосферами

из атомов внедрения. Из-за низкой подвижности дислокаций, а

следовательно, отсутствия микропластической деформации не происходит

релаксации (ослабления) напряжений у вершины хрупкой трещины, чем и

объясняется низкое сопротивление распространению трещин.

Упрочнение при образовании твердого раствора достигает σ

10≅

G. При повышении температуры выше (0,5—0,6) Т

пл

упрочнение за счет

образования твердого раствора сильно уменьшается .

При ограниченном легировании, твердые растворы замещения обладают

достаточной пластичностью и вязкостью и служат ос-

новной матрицей для многих конструкционных и

инструментальных сплавов.

Механические свойства сплавов твердых растворов в сильной

степени зависят от величины зерна, полигонизованной структуры

(субструктуры) и других структурных изменений.

Эффективным барьером для движения дислокаций в металлах

является межзеренная граница — зернограничное упрочнение.

Это объясняется тем, что дислокация не может перейти границу

зерна, так как в новом зерне плоскости скольжения не

совпадают с плоскостью движения этой дислокации. Дальнейшая

деформация продолжается в результате возникновения новой

дислокации в соседнем зерне, поэтому чем мельче зерно

(больше

протяженность границ), тем выше прочность металла (рис. 80,

а).

Зависимость предела текучести от размера зерна описывается

отношением Холла—Петча:

= σ

+ kd

-1/2

где σ

и k — постоянно для данного металла; d — диаметр зерна.

Эта зависимость справедлива и для субзерен. При очень

мелком зерне предел текучести может достигнуть σ

≅

-3

Повышение прочности при измельчении зерна не сопровождается

ох-рупчиванием. Границы зерен и субзерен являются

полупроницаемыми барьерами для движущихся дислокаций. Чем

мельче зерно, тем труднее развивается хрупкая трещина,

поскольку границы зерен затрудняют переход трещины сколом из

одного зерна в другое вследствие изменения ее направления

движения. В то же время, зародышевые

трещины при мелком

зерне меньше.

Измельчение зерна понижает порог хладноломкости (t

На рис. 80, б показано влияние величины зерна стали на

температурный порог хладноломкости. Чем крупнее зерно, тем

выше порог хладноломкости. Для устранения интеркристаллитного

(межзеренного) хрупкого разрушения и понижения t

надо

уменьшать скопление примесей в приграничных объемах

(сегрегацию без выделения) и образование на границах зерен

хрупких фаз (чаще химических соединений), особенно в виде

сплошной сетки.

По данным различных работ при большей величине зерна

трещиностойкость K

1с

возрастает, как это имеет место в стали

(см. рис. 109) и титане. Чем мельче зерно, тем выше предел

выносливости (рис. 80, а), который может быть определен по

формуле

= σ

Rο

+ K

-1/2

, где σ

Rο

и K

—

постоянные, зависящие от материала.

Измельчение зерна модифицированием, термической

обработкой, легированием и т. д. является одним из

перспективных методов упрочнения металлов и сплавов.

Создание в зерне препятствий для движения дислокаций в виде

хорошо развитой субструктуры приводит к дополнительному уп-

115

рочнению. Образование дислокационной структуры по механизму

полигонизации (ячеистой структуры) повышает σ

, мало

изменяя K

1с

и понижает порог хладноломкости (t

)·

Выделение внутри зерен твердого раствора высокодиепереных

равномерно распределенных частиц упрочняющих фаз, например,

в процессе закалки и старения, сильно повышает σ

(дисперсное

упрочнение)

. Упрочнение при старении объясняется

торможением дислокаций зонами Гинье—Престона (ГП) или

частицами выделений.

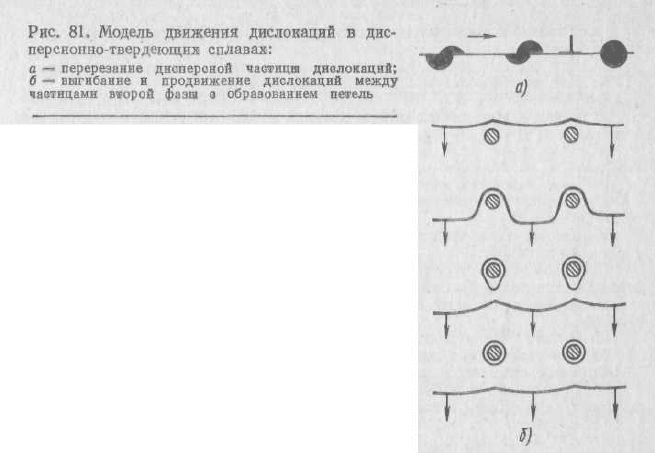
При образовании зон ГП дислокации проходят через них

(перерезают), что требует повышенных напряжений (рис. 81, а).

Зоны ГП имеют модуль сдвига больше, чем у исходного твердого

раствора. Чем прочнее зоны ГП и больше их модуль упругости,

тем труднее они перерезаются дислокациями. Вокруг зон ГП

создается зона значительных упругих напряжений, которая также

тормозит движение дислокаций, а следовательно, способствует

упрочнению при старении.

В случае когерентных частиц избыточной фазы дислокации под

действием приложенных напряжений либо перерезают, либо

огибают эти частицы, что зависит от их размера, прочности и рас-

стояния между ними. В случае некогерентных частиц возможно

только огибание их дислокациями. На (рис. 81, б) показано

сначала выгибание, а затем (при больших напряжениях)

огибание частиц дислокациями. При возрастании напряжений

дислокации образуют замкнутые дислокационные петли

вокруг частиц (рис. 81, б). Оставив вокруг частиц петли,

дислокации продолжают скользить в прежнем направлении (эти

петли или кольца, естественно, препятствуют движению новых

дислокаций). Предел текучести при дисперсном упрочнении

зависит от размера частиц d и их объемной доли f. Уравнение

прочности в этом случае имеет вид:

= σ

+ α√ƒ/ d,

где σ

— напряжение сдвига в матрице; со — коэффициент,

включающий вектор Бюргерса и модуль сдвига G матрицы.

Наибольшее упрочнение наблюдается, когда вторая фаза

дисперсна, равномерно распределена по объему и расстояние

между частицами не велико.

Упрочнение при огибании частиц (при одной объемной доле

выделений второй фазы) всегда менее эффективно, чем упрочнение

при перерезании. Однако вязкость разрушения К

1с

и пластичность

при огибании частиц выше.

Максимальной прочности после дисперсионного старения

соответствует минимальное значение К

1с

. Коагуляция избыточной

В стареющих сплавах протекают два противоположно действующих процесса: 1)

разупрочнение из-за распада пересыщенного твердого раствора; 2) упрочнение вследствие

выделения дисперсных частиц. Эффективносгь упрочнения зависит от соотношения этих

процессов,

116

фазы, снижая прочность (σ

, σ

), повышает

1с

Упрочнение дисперсными частицами

достигает 10

-2

G МПа, но при нагреве до

температуры (0,6—0,75) Т

пл

снижается за

счет их растворения.

Дисперсными частицами часто являются

химические соединения. Чем сложнее

кристаллическая решетка фаза

упрочнителя и чем больше отличается ее

состав от основного твердого раствора, тем

сильнее упрочнение. Химические

соединения, особенно карбиды и нитриды,

имеют высокую твердость, но хрупки.

Например, твердость карбида вольфрама

WC составляет Η1790, карбида титана TiC

- Н2850, нитрида титана TiN - Н323

получения сплавов с высокой констру

нужно, чтобы основной твердый ра

мелкозернистое строение с развитой внут

которой равномерно

0. Таким

образом, для

ктивной прочностью

створ (матрица) имела

ренней субструктурой, в

распределены высоко-дисперсные частицы

упр

н в

и минимальну

) σ

0,2

= 120 МПа?

едует принять при испытании твердости по

юминиевого сплава?

очняющей фазы. Такая структура сплава обеспечивает

получение полупроницаемых барьеров для движущихся дислокаций

и сочетание высокой прочности (σ

, σ

), пластичности (δ, ψ),

вязкости разрушения (К

1с

), вязкости (KCU, KCV, KCT) и низкой

температура вязкохрупкого перехода (по-рор хладноломкости t

)·

Рассмотренные механизмы упрочнения положены в основу

современных технологических процессов повышения

конструктив ой прочности металло и сплавов.

Вопросы для самопроверки

1. Что такое конструктивная прочность и какие параметри используются

для ее оценки?

1. Почему испытания на растяжение наиболее широко применяются по

сравнению с другими видами испытаний?

2. В каких случаях применяюг испытания на статический изгиб?

3. Какое практическое применение может найти вязкость разрушения K

конструкторских разработках?

4. Для каких материалов наиболее целесообразно определять вязкость

разрушения K

5. Какой материал будет иметь максимальную ю

трещиностойкость: 1) σ

0,2

= 500 МПа; 2) σ

0,2

= 1200 МПа; 3

6. Какую нагрузку сл

Бринеллю стали, медного и ал

117

8. Каким способом надо измерять твердость листовой мягкой стали

толщиной 1 мм?

9. Как связано число твердости НВ с временным сопротивлением σ

10. Для чего используются динамические испытания?

11. Что больше — KCU, KCV или КСТ одного и того же материала? Почему?

12. В каком случае будет меньше разность между KCV и КСТ — у

пластичного или у хрупкого материала?

13. Какими методами определяется порог хладноломкости и как можно

использовать на практике знание температурного запаса вязкости?

14. Чем

отличается малоцикловая усталость от многоцикловой?

15. Определить приближенно предел выносливости σ

-1

для стали с σ

= 800

МПа?

16. Как меняется предел выносливости при переходе от гладких образцов

к образцам с надрезом?

17. Какой образец будет иметь более высокий предел выносливости —

шлифованный или полированный?

18. Назовите основные виды изнашивания и повреждаемости при трении

в машинах?

19. Почему окислительное изнашивание считают допустимым?

20. Чем различаются повреждения при схватывании I

и II рода?

21. Какие существуют методы упрочнения металлов?

22. Предложите способы существенного упрочнения металла без сильного

снижения пластичности и вязкости разрушения?

ГЛАВА VIII. ЖЕЛЕЗО И СПЛАВЫ НА ЕГО ОСНОВЕ

Сплавы железа распространены в промышленности наиболее

широко. Основные из них — сталь и чугун — представляют собой

сплавы железа с углеродом. Для получения заданных свойств в

сталь и чугун вводят легирующие элементы. Ниже рассмотрено

строение и фазовые превращения в сплавах железо—углерод, а

также фазы в сплавах железа с легирующими элементами.

1. КОМПОНЕНТЫ И ФАЗЫ

В СИСТЕМЕ ЖЕЛЕЗО — УГЛЕРОД

Железо — металл сероватого цвета. Атомный номер 26,

атомная масса 55,85, атомный радиус 0,127 нм. Чистое железо,

которое может быть получено в настоящее время, содержит

99,999 % Fe, технические сорта 99,8—99,9 % Fe. Температура

плавления железа 1539 °С. Железо имеет две полиморфные

модификации α и γ. Модификация «-железа существует при

температурах ниже 910 °С и выше 1392 °С (рис. 82). В интервале

температур 1392—1539 °С α-железо нередко обозначают как

δ-

железо.

Кристаллическая решетка α-железа — объемно центрированный

куб с периодом решетки 0,28606 нм. До температуры 768 °С α-

железо магнитно (ферромагнитно). Температуру 768 °С,

соответствующую магнитному превращению, т. е. переходу из

ферромагнитного состояния в парамагнитное, называю)? точкой

Кюри и обозначают A

Плотность α-железа 7,68 г/см

118

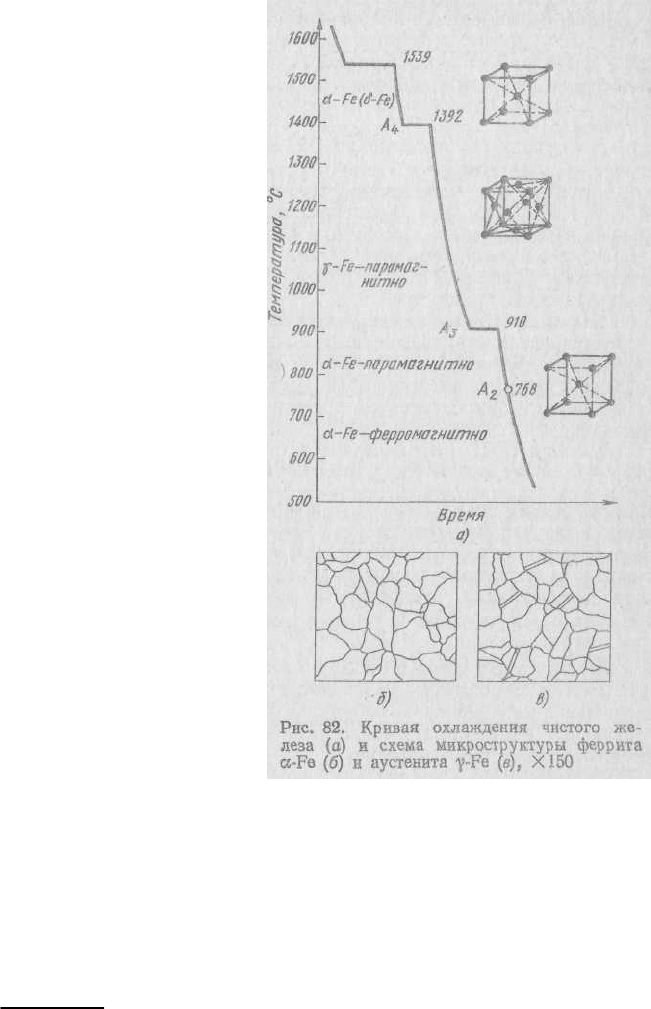
γ-железо существует

при температуре 910—

1392 °С; оно парамагнитно.

Кристаллическая решетка

γ-железа гранецентриро-

ванная кубическая (a =

0,3645 нм при 910 °С).

Критическую точку

превращения α

⇔ γ (рис. 82)

при 910 °С обозначают

соответственно Ас

(при

нагреве) и Аr

(при

охлаждении). Критическую

точку перехода γ5α при

1392 °С обозначают Ас

(при нагреве) и Ас

(при

охлаждении)

Углерод является

неметаллическим

элементом II периода IV

группы периодической

системы, атомный номер

6, плотность 2,5 г/см

температура плавления

3500 °C, атомный радиус

0,077 нм. Углерод

полиморфен. В обычных

условиях он находится в

виде модификации

графита, но может

существовать и в виде

метаста-бильной

модификации алмаза.

Углерод растворим в

железе в жидком и

твердом состояниях, а

также может быть в виде

химического соединения — цементита, а в высокоуглеродистых

сплавах и в виде графита.

В системе Fe—C различают следующие фазы: жидкий сплав,

твердые растворы—феррит и аустенит, а также цементит и

графит.

Феррит (Ф) — твердый раствор углерода и других примесей

в α-железе. Различают низкотемпературный α-феррит о

растворимостью урлерода до 0,02 % и высокотемпературный δ-

феррит с

Обозначения Ас и Ar происходят от начальных букв французских слов: А —

arreter — остановка (площадка на кривой охлаждения), с — choffage — нагрев и r-

refroidissmont — охлаждение.

119

предельной растворимостью углерода 0,1 %. Атом углерода

располагается в решетке феррита в центре грани куба, где

помещается сфера радиусом 0,29 атомного радиуса железа, а

также в вакансиях, на дислокациях и т. д. Под микроскопом

феррит выявляется в виде однородных полиэдрических зерен (см.

рис. 82, б).

Феррит (при 0,06 % С) имеет примерно следующие

механические свойства: σ

= 250 МПа, σ

0,2

= 120 МПа, δ 50

%, ψ

80 %, 80—90 НВ.

≅

Аустенит (А) — твердый раствор урлерода и других примесей

в γ-железе. Предельная растворимость углерода в γ-железе —

2,14 %. Атом углерода в решетке γ-железа располагается в центре

элементарной ячейки (см. рис 29, б), в которой может поместиться

сфера радиусом 0,41R (R — атомный радиус железа) и а

дефектных областях кристалла.

Различные объемы элементарных сфер в ОЦК и ГЦК решетках

и предопределили значительно большую растворимость углерода

в γ-железе по сравнению с растворимостью в α-железе. Аустенит

обладает высокой пластичностью, низкими пределами текучести

и прочности. Микроструктура аустенита — полиэдрические зерна

(рис. 82, в).

Цементит (Ц) — это химическое соединение железа с

углеродом — карбид железа Fe

C В цементите содержится 6,67 %

С Цементит имеет сложную ромбическую решетку с плотно й

упаковкой атомов. Температура плавления цементита точно не

определена в связи с

ВОЗМОЖНОСТЬЮ его распада. До температуры

210 °С, обозначаемой А

, цементит ферромагнитен. К характерным

особенностям цементита относятся высокая твердость 1000 HV и

очень малая пластичность. Цементит является метастабильной

фазой. В условиях равновесия в сплавах с высоким содержанием

углерода образуется графит.

Графит имеет гексагональную слоистую (см. рис. 88, а)

кристаллическую решетку. Межатомные расстояния в решетке

небольшие и составляют 0,142 нм, расстояние между плоскостями

равно 0,340 нм. Графит мягок, обладает низкой прочностью и

электрической проводимостью.

В сплавах Fe—С существуют две высокоуглеродистые фазы:

метастабильная — цементит и стабильная — графит. Поэтому

различают две диаграммы состояния — метастабильную Fe—

C и стабильную Fe—С (графит).

2. ДИАГРАММА СОСТОЯНИЯ ЖЕЛЕЗО —

ЦЕМЕНТИТ (МЕТАСТАБИЛЬНОЕ РАВНОВЕСИЕ)

На диаграмме состояния железо — цементит (рис. 83)

даны фазовый состав и структура сплавов

G концентрацией от

чистого железа до цементита (6,67 % С).

Система Fe—Fe

C метастабильная. Образование цементита

вместо графита дает меньший выигрыш энергии Гиббса, однако

кинетическое образование карбида железа более вероятно.

120