Лабораторная работа №1 Линейная парная регрессия
Подождите немного. Документ загружается.

Лабораторная работа №1 «Модель парной линейной регрессии».
2 курс 3 поток.
Группа
ФИО
Исходные данные лабораторной работы представлены в таблице №1.
Таблица №1.
По имеющимся данным
1. Вычислить дескриптивные (описательные) статистики:
1) выборочные средние;
2) выборочную дисперсию;
3) выборочное среднее квадратичное отклонение;
4) нижний и верхний квартили выборочного распределения;
5) размах выборки;
6) 95% доверительные интервалы для оценки математического ожидания.
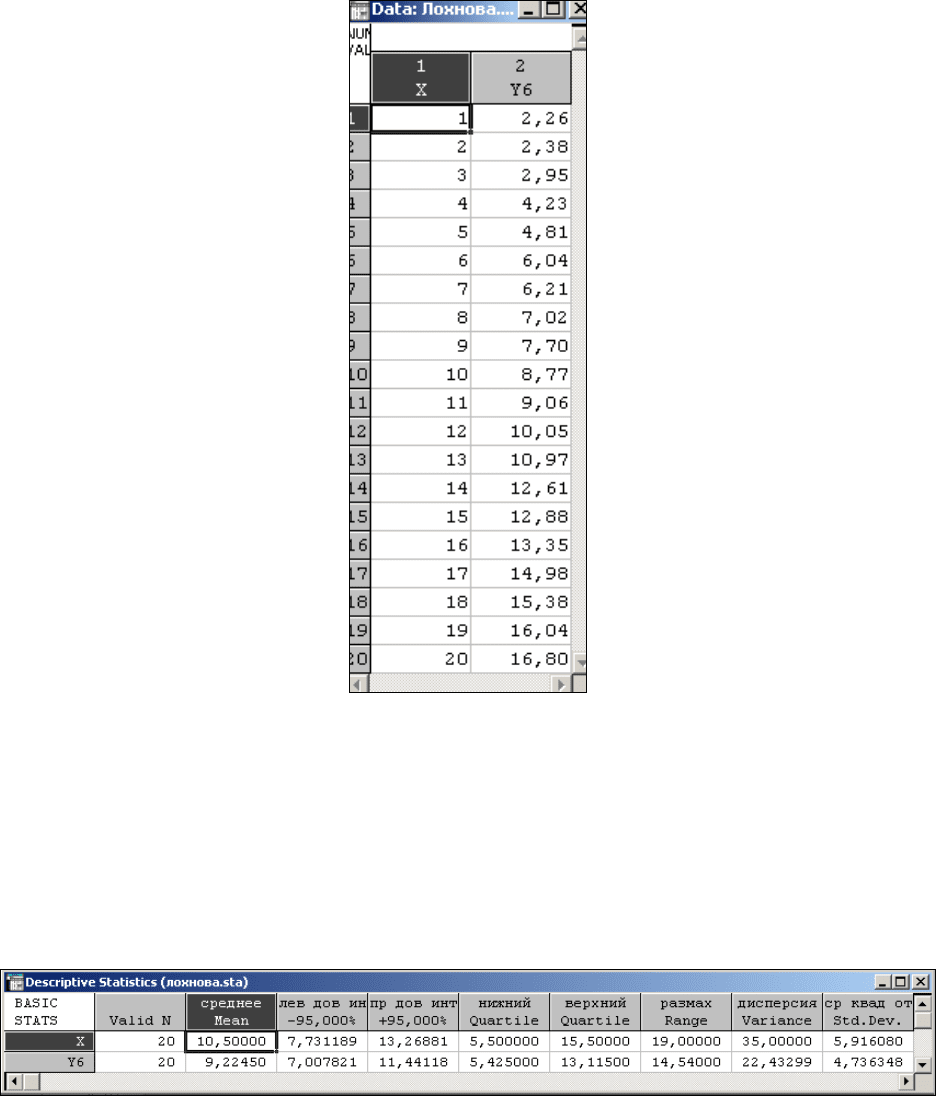
Результаты расчета приведены в таблице №2.
Таблица №2.
2. Вычислить выборочный коэффициент корреляции и оценить его значимость на
5% уровне.
Результаты расчеты приведены в таблице №3.
Таблица №3.
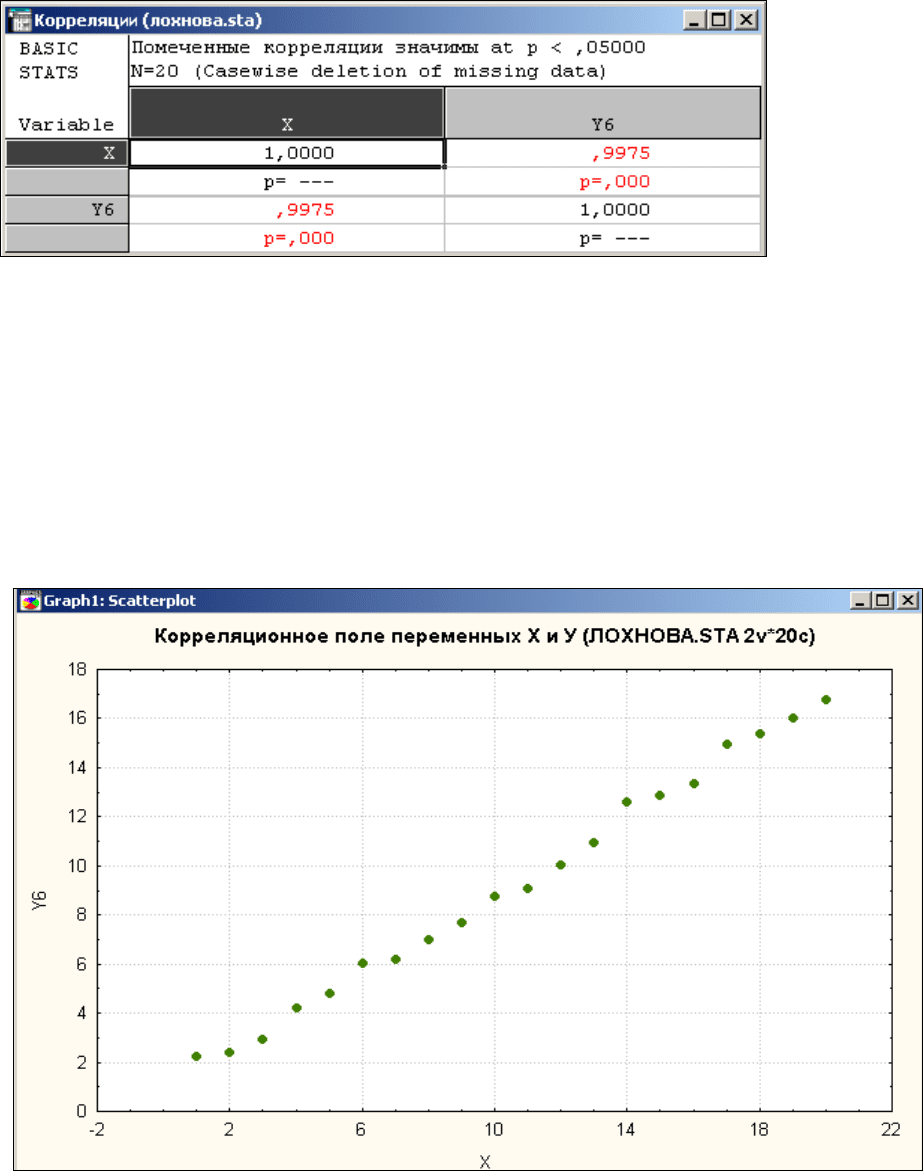
Коэффициент корреляции показывает тесноту связи между переменными Х и У,
если коэффициент корреляции положительный, то связь прямая. А если отрицательный,
то связь обратная. Коэффициент корреляции лежит в интервале [-1,+1]. Чем ближе
коэффициент корреляции к концам интервала (к -1 или к +1), тем теснее связь между Х и
У. Чем ближе коэффициент корреляции к нулю, тем слабее связь между Х и У.
Высокое значение коэффициента корреляции в таблице №3 0,9975 указывает на
тесную связь между Х и У в представленных данных. Поэтому ниже пойдет речь о
выяснение конкретной формы данной связи, т.е. о построение модели парной регрессии.
3. Построить корреляционное поле заданных переменных и сформулировать
гипотезу о виде связи.
График корреляционного поля представлен на рисунке №1 .
Рис.1 Корреляционное поле.
Из вида корреляционного поля делаем вывод, что модель парной регрессии нужно
строить в виде прямой регрессии.
4. Вычислить параметры уравнения парной регрессионной модели.
Параметры регрессионной модели в пакете СТАТИСТИКА можно вычислить двумя
способами. Первый способ – простой, наглядный использует возможности графики
пакета. Второй способ - перейти в модуль множественная регрессия. Этот способ
позволяет не только найти параметры модели, но и подробно исследовать качества и
прогнозирующие свойства модели.
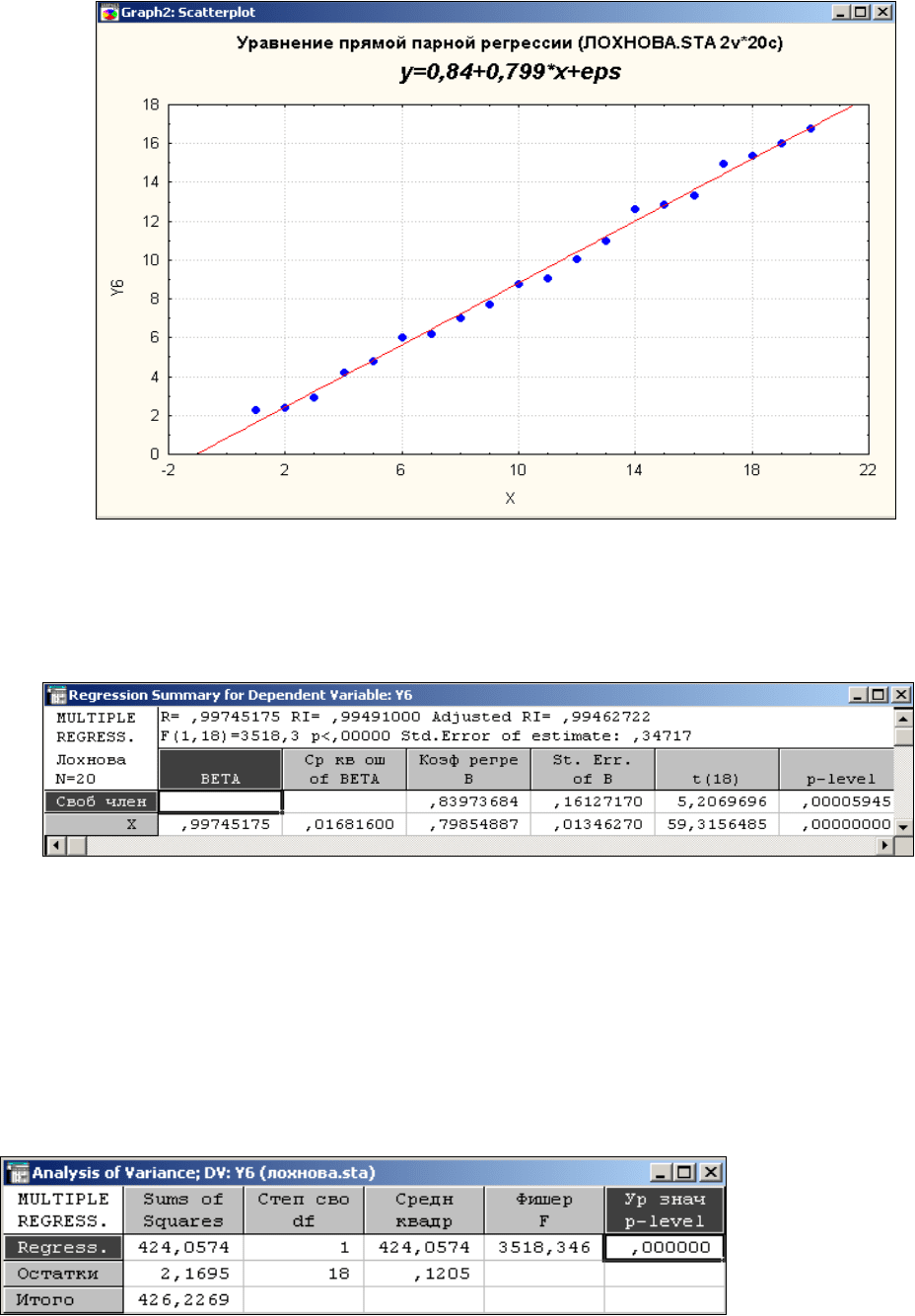
Сначала исследуем модель первым способом. Результаты расчетов представлены на
рисунке 2.
Рис.2 Уравнение парной регрессии.
Свободный член уравнения равен 0,84.
Угловой коэффициент при Х равен 0,799.
Проведем расчеты коэффициентов парной регрессии вторым способом, т.е. модулем
множественной регрессии. Результаты расчета представлены в таблице №4.
Таблица №4.
b
0
=0,84;
b
1
=0,799;
s(b
0
)=0,161;
s(b
1
)=0,013.
В последнем столбце таблицы №4 указана вероятность того, что коэффициенты
модели незначимы. Практически нулевая вероятность дает основание полагать, что все
коэффициенты модели значимы.
5. Оценить значимость построенного уравнения регрессии с помощью F-критерия.
Результаты расчетов занесем в таблицу №5.
Таблица №5.
Большое значение критерия Фишера и нулевой уровень значимости показывает, что
уравнение значимо и хорошего качества.
6. Оценить качество построенного уравнения регрессии с помощью коэффициента
детерминации R
2
.
Коэффициент детерминации получаем из таблицы №6.
Таблица №6.
Из таблицы №6 получаем R
2
=0,99491. Так как R
2
близкий к 1, то это также указывает
на высокое качество уравнения регрессии.
7. Построить 95%-ные интервалы для оценок параметров уравнения регрессии.
Формулы для расчетов доверительных интервалов приведем ниже:
)].(*);(*[
)];(*);(*[
11111
00000
bstbbstb
bstbbstb
b
0
, b
1
, s(b
0
), s(b
1
) возьмем из таблицы №4. Найдем
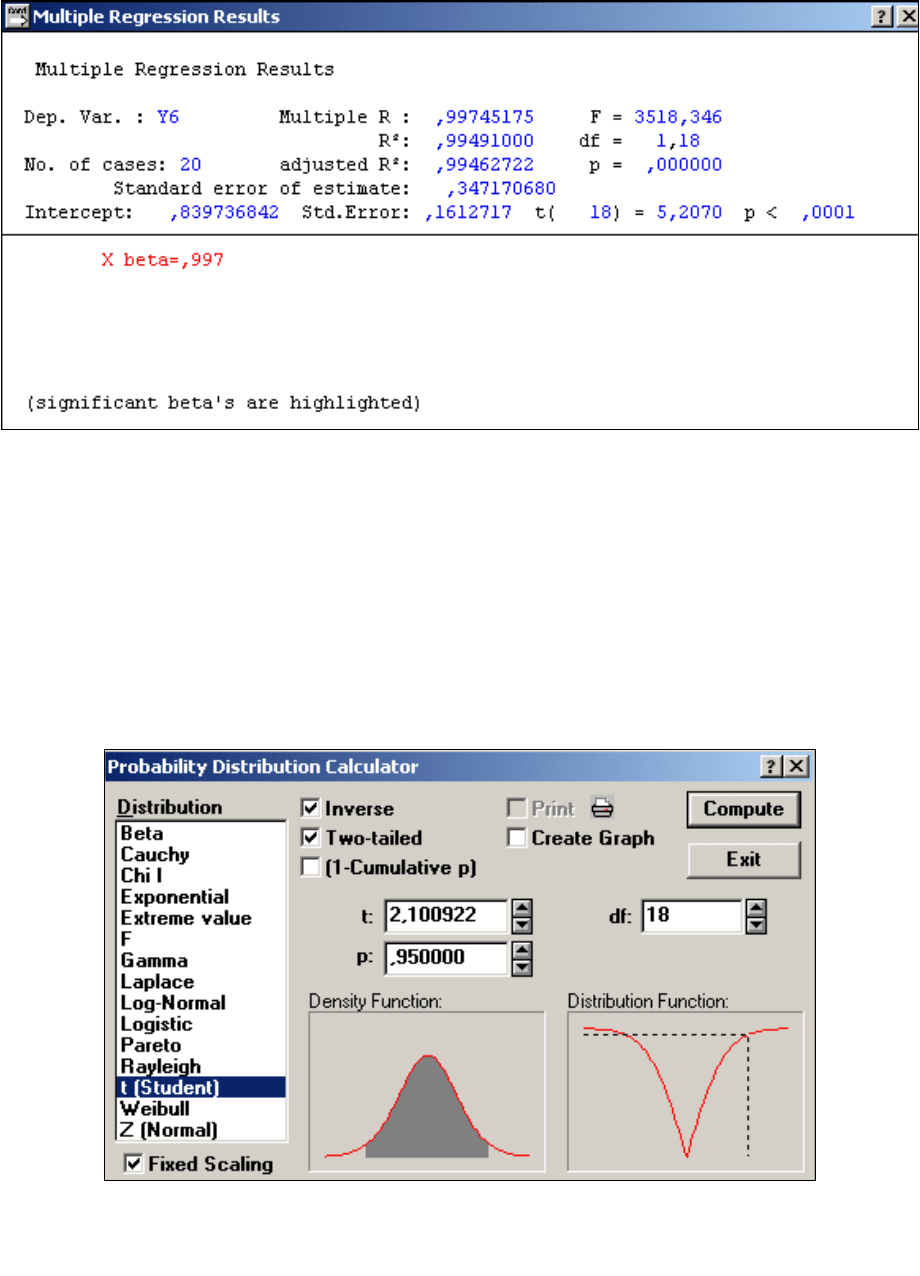
t
с помощью вероятностного
калькулятора из пакета STATISTICA.
Расчеты приведены в таблице №7.
Таблица №7.
Из таблицы №7 видно, что
t
=2,100922.
0
[0,84-2,100922*0,161; 0,84+2,100922*0,161]=[ 0,501752; 1,178248];
1
[0,799-2,100922*0,013; 0,799+2,100922*0,013]=[ 0,771688; 0,826312].
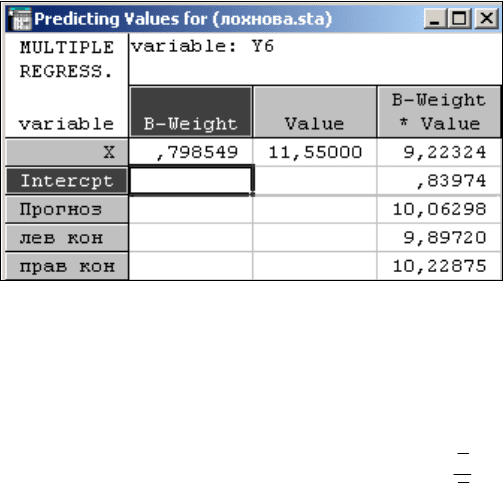
8. Рассчитать прогнозное значение, если значение независимой переменной
увеличится на 10% от его среднего значения. Построить 95% доверительный
интервал для прогнозного значения.
Прогнозное значение =10,5*1,1=11,55.
Расчеты прогнозного значения У и доверительного интервала для У проведем в
модуле множественной регрессии представлены в таблице №8.
Таблица №8.
Прогнозное значение=10,06298.
95% доверительный интервал
[9,89720;10,22875].
9. Оценить с помощью коэффициента эластичности (среднего) силу связи
независимой переменной с зависимой.
Коэффициент эластичности рассчитывается по следующей формуле:
y
x
bЕ *
1
.
Коэффициент эластичности показывает на сколько процентов изменится У, если Х
изменить на 1%. Положительный коэффициент эластичности означает, что У изменяется в
том же направление, что и Х. Отрицательный коэффициент эластичности означает, что У
изменяется в противоположном Х направление. В результате вычислений получаем:
Е=0,799*10,5/9,2245=0,9094802.
Если у нас Х изменить на 1%, то У изменится на 0,9094802%.
10. Рассчитать параметры уравнений регрессий других форм: степенной,
логарифмической, экспоненциальной и др.
Исходная таблица расчетов степенной модели в модуле «нелинейное оценивание»
пакета STATISTICA.
Таблица №9.
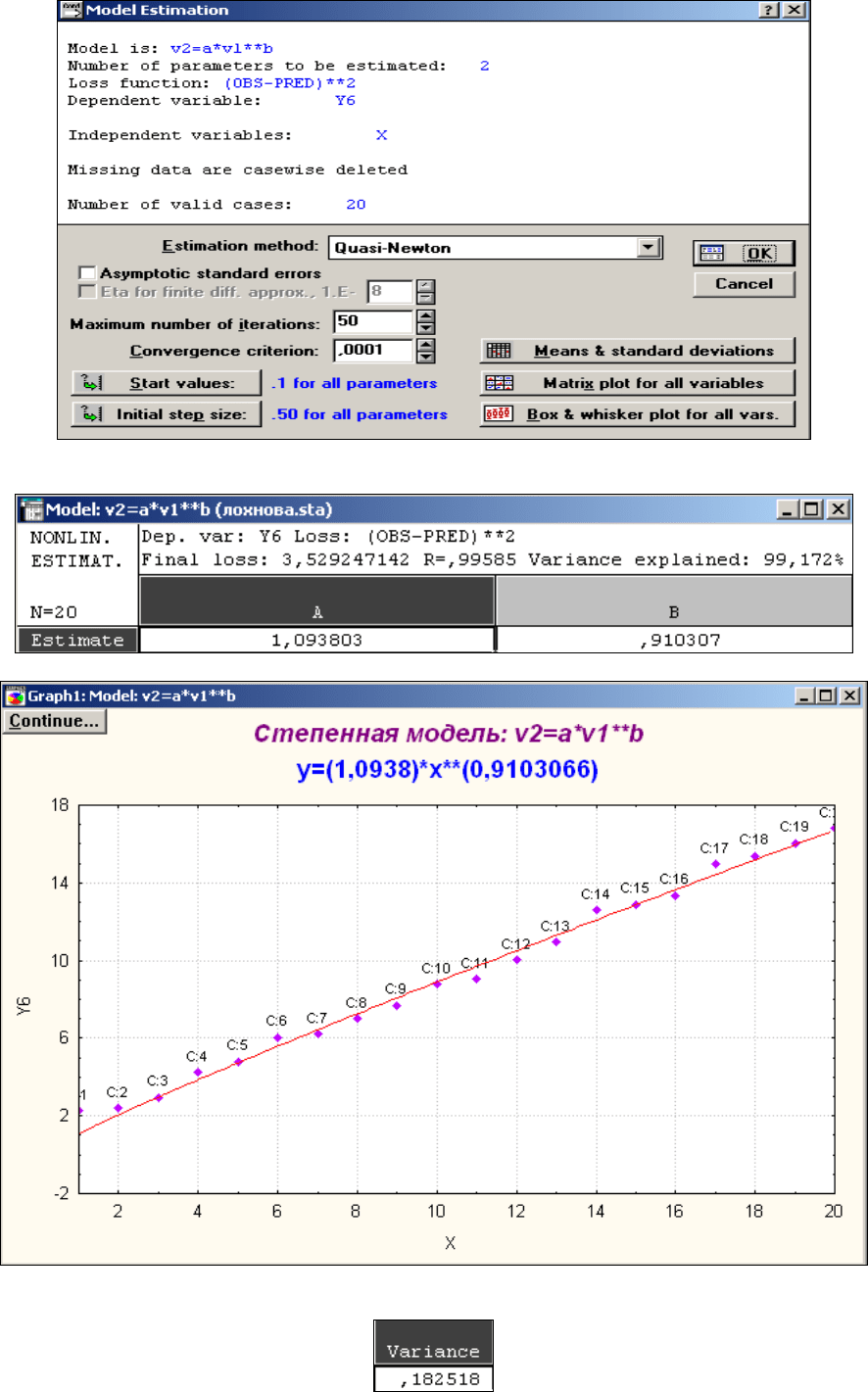
Расчетные коэффициенты модели получены в таблице №10.
Таблица №10.
График степенной зависимости на рисунке №3.
Рис.3 Степенная зависимость.
Найдем дисперсию остатков модели.
Дисперсия остатков модели равна 0,182518.
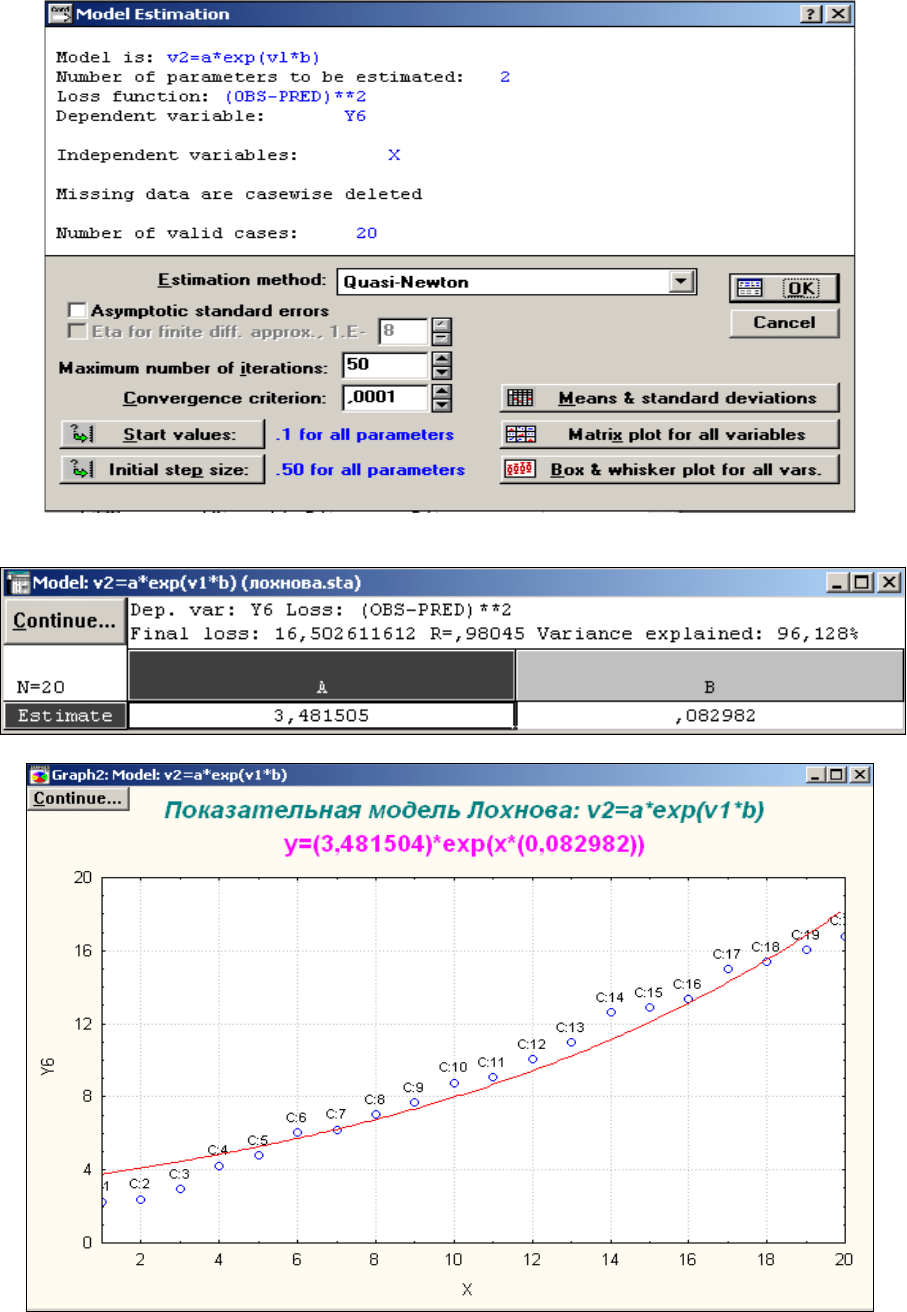
Перейдем к показательной (экспоненциальной) модели.
Исходная таблица расчетов показательной модели в модуле «нелинейное оценивание»
пакета STATISTICA.
Таблица №11.
Расчетные коэффициенты модели получены в таблице №12.
Таблица №12.
График показательной зависимости представлен на рисунке 4.
Рис.4 Показательная зависимость.
Найдем дисперсию остатков модели.
Дисперсия остатков показательной модели равна 0,861452.
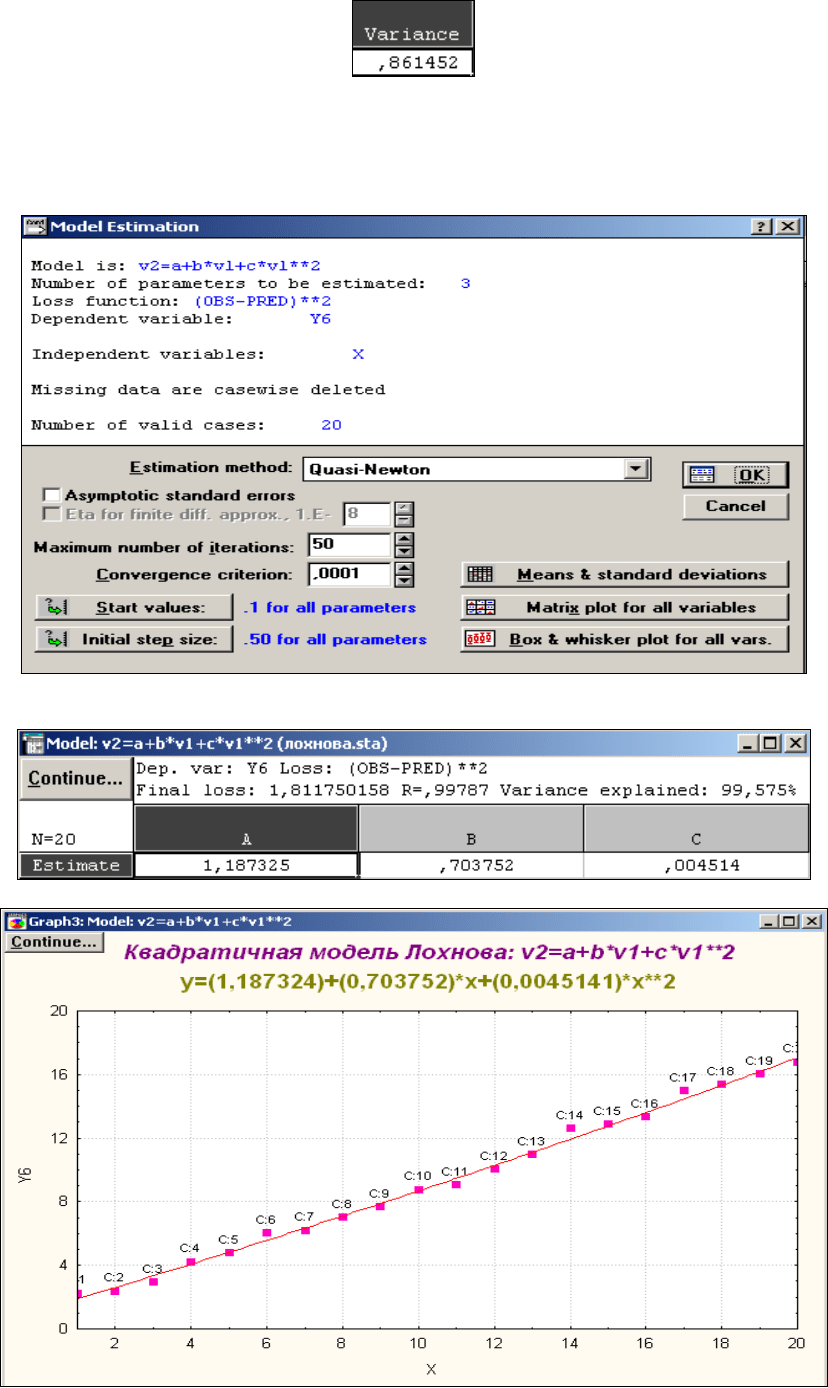
Перейдем к квадратичной модели.
Исходная таблица расчетов квадратичной модели в модуле «нелинейное оценивание»
пакета STATISTICA.
Таблица №13.
Расчетные коэффициенты модели представлены в таблице №14.
Таблица №14.
График квадратичной зависимости представлен на рисунке №5.
Рис.5 Квадратичная зависимость.
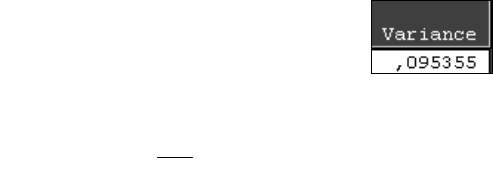
Найдем дисперсию остатков модели.
Дисперсия остатков квадратичной модели равна 0,095355.
Рассмотрим акаике критерий сравнения моделей.
n
К
А
остк
2
)ln(
2
К=1 – для степенных и показательных моделей;
К=2 – для квадратичной модели;
n- число наблюдений = 20.
Считается лучшая модель такая, где критерий Aкаике минимальный.
Ак (степ)=ln(0.182518)+2*1/20=-1.6;
Aк (показ)=ln(0.861452)+2*1/20=-0.049;
Ак (квадр)=ln(0.095355)+2*2/20=-2.55.
Для дальнейшего использования выбираем квадратичную модель, т.к. критерий
Aкаике принимает минимальное значение.
