Labelle P. Supersymmetry DeMYSTiFied
Подождите немного. Документ загружается.


306
Supersymmetry Demystified
us to write the second term as
q χσ
μ
¯χ A
μ
=−q ¯χ ¯σ
μ
χ A
μ
so that the two terms of Eq. (13.22) can be combined into
i ¯χ ¯σ
μ
∂
μ
χ −q ¯χ ¯σ
μ
χ A
μ
= i ¯χ ¯σ
μ
D
μ
χ
with D
μ
again defined by Eq. (13.21).
Using covariant derivatives, Eq. (13.19) therefore can be simplified to
†
e
2qV
D
=(D
μ
φ)
†
(D
μ
φ) + i ¯χ ¯σ
μ
D
μ
χ + FF
†
−q φ
†
φ D
−
√
2 q χ · λφ
†
+ h.c.
(13.23)
which, apart from three missing terms, is exactly the lagrangian for the interaction
of a left-chiral Weyl spinor with an abelian gauge field we obtained in Eq. (10.54)!
It’s in order to get this simple equality, with no overall factor, that a factor of 2 is
included in the exponential containing V.
The missing terms are those that contain only the fields of the gauge superfield,
namely, A
μ
(x), λ(x), and D(x). We now turn our attention to figuring out how
these terms can be recovered in the superfield approach.
13.3 Lagrangian of a Free Supersymmetric
Abelian Gauge Theory in Superfield
Notation
What we would like to introduce is a field-strength superfield F that would contain
the gauge-invariant field strength F
μν
[recall that in the case of a U (1) gauge theory,
the field strength is gauge invariant; this is no longer true for nonabelian gauge
theories, but we will discuss those later]. As a SUSY partner of this field strength,
we would like to still use the same fields that appear in V, i.e., the photino field λ
and the auxiliary field D, which are gauge invariants, as we have just seen. In this
way, all the components of the field-strength superfield would be gauge invariant,
and it would be trivial to get a gauge-invariant lagrangian.
Now, to build this field-strength superfield, we could do it the hard way: using
brute force to find some combination of λ, F
μν
, and D whose SUSY transformation

CHAPTER 13 Gauge Field Theories
307
will reproduce the correct transformations of the component fields. This is extremely
long and extremely painful. Or we can do it the “easy” way: starting from the
superfield V and applying the “SUSY derivatives” D
a
and
¯
D
˙a
to generate the field-
strength superfield. This is merely long and painful. We will choose the “long and
painful” approach over the “extremely long and extremely painful” one. Actually,
the calculation itself is not too bad; it’s just painful to type!
We need to apply at least three SUSY derivatives to V because if we apply fewer,
the photon field A
μ
(with no derivative acting on it) will remain present, and our
result therefore will not be gauge-invariant. This is obvious if you recall that D
a
contains a derivative with respect to θ
a
and that
¯
D
˙a
contains a derivative with respect
to
¯
θ
˙a
[see Eqs. (11.57), (11.58), and (11.61)]. The standard choice is to define the
field-strength superfield F
a
as
F
a
≡
¯
D ·
¯
DD
a
V (13.24)
The reason for choosing this particular combination of derivatives will soon become
clear.
The superfield F carries a lower undotted index, which is just a fancy way of
saying that it transforms like a left-chiral Weyl spinor under Lorentz transformations
(unlike all the other superfields we have introduced so far, which are scalars).
Note that F
a
is a left-chiral superfield! Indeed, because of Eq. (11.62), F
a
satisfies
¯
D
˙
b
F
a
= 0
which defines a left-chiral superfield. Unlike the we worked with in Chapter 12,
F
a
is a spinor left-chiral superfield, not a scalar left-chiral superfield.
An obvious thing to check is whether this field-strength superfield is invariant
under the super gauge transformation in Eq. (13.3) like its nonsupersymmetric
counterpart F
μν
. Under that transformation, we have
F
a
→ F
a
−i
¯
D ·
¯
DD
a
+i
¯
D ·
¯
DD
a
†
(13.25)
where we have used the fact that the SUSY derivatives are linear operators to
distribute them. Now recall that is a left-chiral superfield and that applying D
a
to the hermitian conjugate of a left-chiral superfield gives zero [see Eq. (12.4)].
Therefore, the last term of Eq. (13.25) is identically zero. We still have to show that
the second term on the right-hand side also vanishes. We will use an anticommutator
to move a
¯
D
˙a
so that it will act directly on the left-chiral superfield and then use

308
Supersymmetry Demystified
the fact that
¯
D
˙a
= 0 because is left-chiral. We have (recall that
¯
D
˙a
and
¯
D
˙a
anticommute)
¯
D
˙a
¯
D
˙a
D
b
=−
¯
D
˙a
¯
D
˙a
D
b
=−
¯
D
˙a
{
¯
D
˙a
, D
b
} +
¯
D
˙a
D
b
¯
D
˙a
=−
¯
D
˙a
{D
b
,
¯
D
˙a
}
=−i (σ
μ
)
b ˙a
¯
D
˙a
∂
μ
(13.26)
where in the last step we have used Eq. (11.63). We obviously may move the
operator
¯
D
˙a
through the partial derivative ∂
μ
(they commute), so we end up with
¯
D
˙a
¯
D
˙a
D
b
=−i (σ
μ
)
b ˙a
∂
μ
¯
D
˙a
= 0
This completes the proof that the last two terms of Eq. (13.25) vanish and that F
a
is gauge-invariant.
The next step is to calculate explicitly F
a
in terms of component fields. This
requires working out explicitly the right-hand side of Eq. (13.24). This calculation
is nontrivial and requires a few special tricks, so we will devote a section to it.
13.4 The Abelian Field-Strength Superfield
in Terms of Component Fields
We will now explicitly calculate the right-hande side of Eq. (13.24), where the
vector superfield V is given in Eq. (13.10) (in the Wess-Zumino gauge). It turns out
that the calculation is much simpler if we trade the variables x
μ
,θ, and
¯
θ for the
variables y
μ
,θ
, and
¯
θ
defined by
y
μ
= x
μ
−
i
2
θσ
μ
¯
θ
θ
= θ
¯
θ
=
¯
θ (13.27)
The relation between y
μ
and x
μ
is the same as before [see Eq. (12.3)]. Recall that
σ
μ
carries lower indices, so we may write the relation between y
μ
and x
μ
more
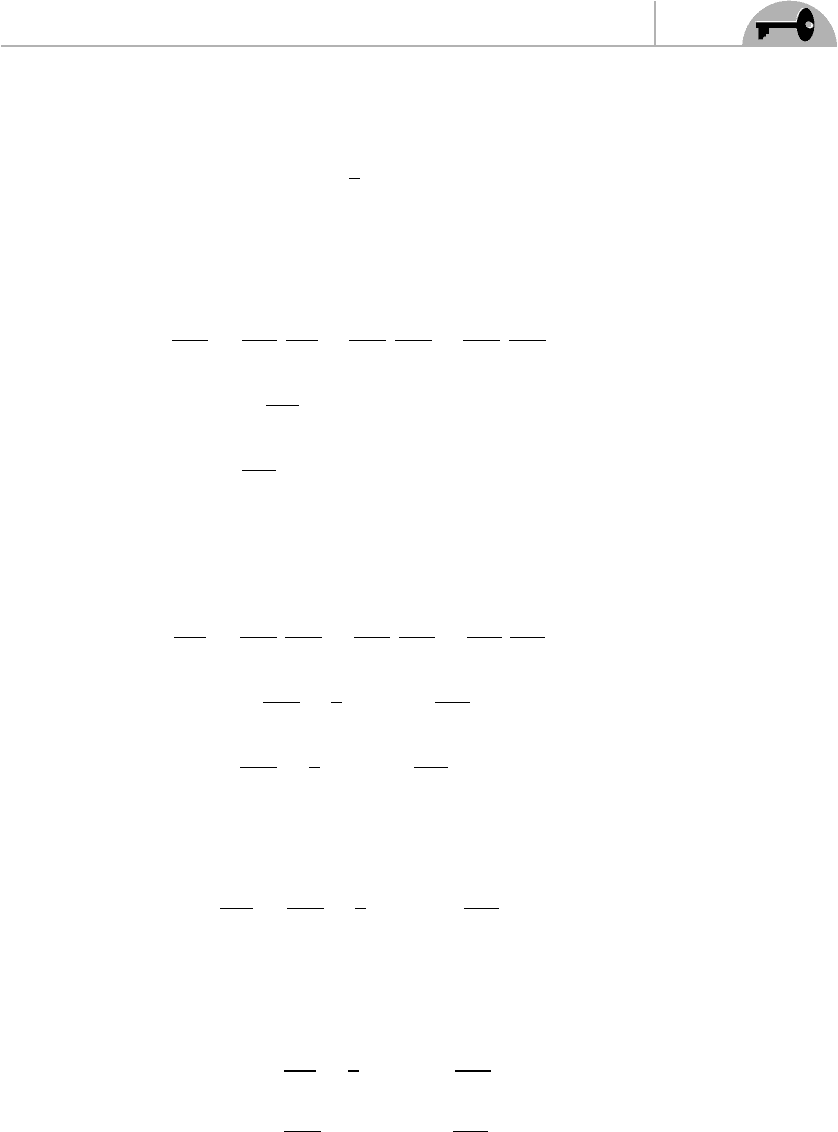
CHAPTER 13 Gauge Field Theories
309
explicitly as
y
μ
= x
μ
−
i
2
θ
a
(σ
μ
)
a
˙
b
¯
θ
˙
b
Now we will express the partial derivatives with respect to the first set of variables
in terms of partial derivatives with respect to the second set. We have
∂
∂x
μ
=
∂y
ν
∂x
μ
∂
∂y
ν
+
∂θ
a
∂x
μ
∂
∂θ
a
+
∂
¯
θ
a
∂x
μ
∂
∂
¯
θ
a
= δ
ν
μ
∂
∂y
ν
=
∂
∂y
μ
(13.28)
The derivatives with respect to the Grassmann variables are more interesting. For
example,
∂
∂θ
a
=
∂θ
b
∂θ
a
∂
∂θ
b
+
∂
¯
θ
b
∂θ
a
∂
∂
¯
θ
b
+
∂y
μ
∂θ
a
∂
∂y
μ
= δ
b
a
∂
∂θ
b
−
i
2
(σ
μ
)
a
˙
b
¯
θ
˙
b
∂
∂y
μ
=
∂
∂θ
a
−
i
2
(σ
μ
)
a
˙
b
¯
θ
˙
b
∂
∂y
μ
(13.29)
where we have used the fact that
¯
θ =
¯
θ
in the last step. A similar calculation leads to
∂
∂
¯
θ
˙a
=
∂
∂
¯
θ
a
+
i
2
θ
b
(σ
μ
)
b ˙a
∂
∂y
μ
Let us now go back to the SUSY derivatives. We find [see Eqs. (11.57) and
(11.58)]
D
a
=
∂
∂θ
a
−
i
2
(σ
μ
)
a
˙
b
¯
θ
˙
b
∂
∂x
μ
=
∂
∂θ
a
−i (σ
μ
)
a
˙
b
¯
θ
˙
b
∂
∂y
μ
(13.30)
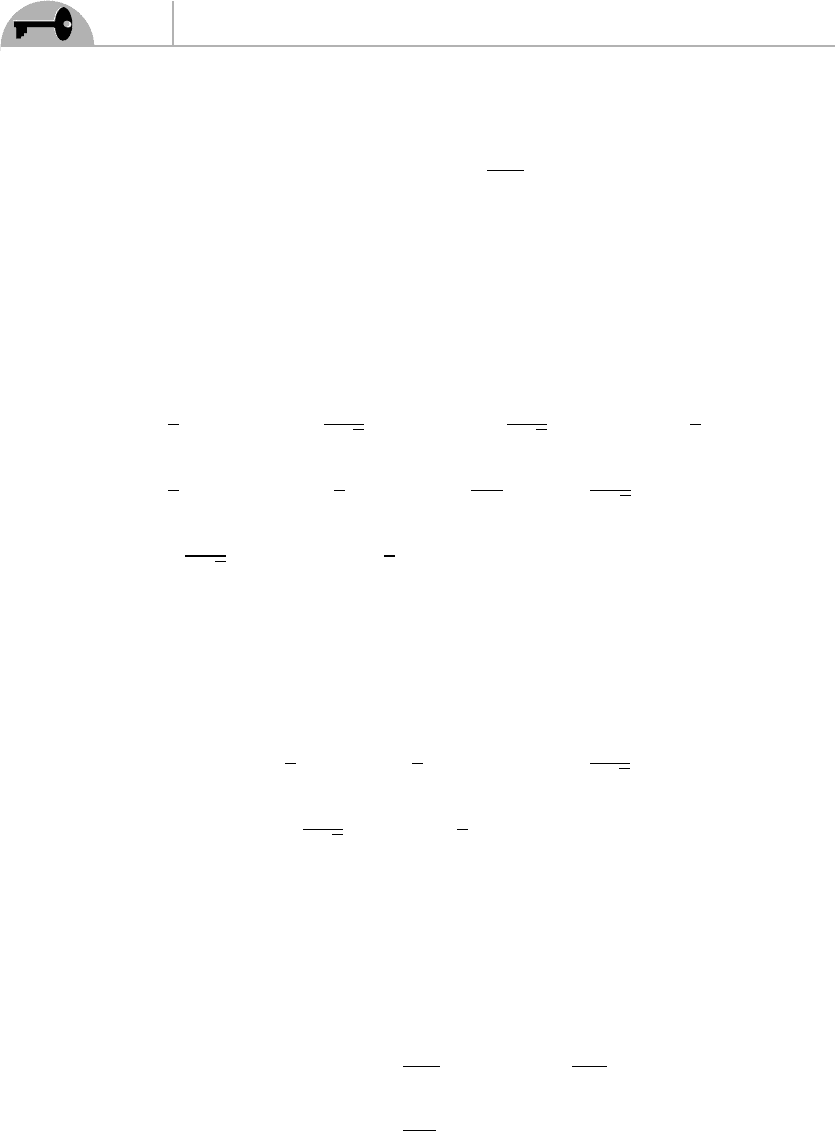
310
Supersymmetry Demystified
whereas
¯
D
˙a
=
∂
∂
¯
θ
˙a
It is the simplicity of this second expression that makes it worthwhile to change
variables.
Before calculating the field-strength superfield, we need to express the vector
superfield [Eq. (13.10)] in terms of the new variables. We simply replace x
μ
by
y
μ
+i θ
σ
μ
¯
θ
/2 and Taylor expand. Keeping in mind that any expression with three
θ or three
¯
θ vanishes identically, we get a simple result:
V =
1
2
θσ
μ
¯
θ A
μ
(x) +
1
2
√
2
θ ·θ
¯
θ ·
¯
λ(x) +
1
2
√
2
¯
θ ·
¯
θθ · λ(x) −
1
8
θ ·θ
¯
θ ·
¯
θ D(x)
=
1
2
θ
σ
μ
¯
θ
A
μ
(y) +
i
4
θ
σ
μ
¯
θ
θ
σ
ν
¯
θ
∂
∂y
ν
A
μ
(y) +
1
2
√
2
θ
· θ
¯
θ
·
¯
λ(y)
+
1
2
√
2
¯
θ
·
¯
θ
θ
· λ(y) −
1
8
θ
· θ
¯
θ
·
¯
θ
D(y)
To simplify the notation, we will drop the prime on the Grassmann variables and not
write explicitly the y dependence of the fields. We also will use ∂
μ
for the derivative
with respect to y
μ
. The second term on the right-hand side can be simplified by
using Eq. (A.56). We then get
V =
1
2
θσ
μ
¯
θ A
μ
+
i
8
θ ·θ
¯
θ ·
¯
θ∂
μ
A
μ
+
1
2
√
2
θ ·θ
¯
θ ·
¯
λ
+
1
2
√
2
¯
θ ·
¯
θθ · λ −
1
8
θ ·θ
¯
θ ·
¯
θ D (13.31)
We are finally ready to compute
F
a
=
¯
D ·
¯
DD
a
V
We start by applying to Eq. (13.31) the SUSY derivative
D
a
=
∂
∂θ
a
−i (σ
μ
)
a
˙
b
¯
θ
˙
b
∂
∂y
μ
=
∂
∂θ
a
−i (σ
μ
)
a
˙
b
¯
θ
˙
b
∂
μ
(13.32)

CHAPTER 13 Gauge Field Theories
311
where we again have dropped the prime on the Grassmann variables and used the
notation ∂
μ
= ∂/∂y
μ
.
We get
D
a
V =
1
2
(σ
μ
)
a
˙
b
¯
θ
˙
b
A
μ
+
i
4
θ
a
¯
θ ·
¯
θ∂
μ
A
μ
+
1
√
2
θ
a
¯
θ ·
¯
λ +
1
2
√
2
¯
θ ·
¯
θλ
a
−
1
4
θ
a
¯
θ ·
¯
θ D −
i
2
(σ
μ
)
a
˙
b
¯
θ
˙
b
θσ
ν
¯
θ∂
μ
A
ν
−
i
2
√
2
θ ·θ(σ
μ
)
a
˙
b
¯
θ
˙
b
¯
θ ·∂
μ
¯
λ
(13.33)
We now need to apply
¯
D ·
¯
D to Eq. (13.33). Luckily for us, in terms of the new
variables, this is simply
¯
D ·
¯
D =
¯
∂
˙a
¯
∂
˙a
=
∂
∂
¯
θ
˙a
∂
∂
¯
θ
˙a
(13.34)
We see that we may drop the two terms in Eq. (13.33) containing only one
¯
θ.As
for the other terms, it will make our life easier if we can get all the
¯
θ to be dotted
together, i.e., in the form
¯
θ ·
¯
θ. For example, consider the combination
(σ
μ
)
a
˙
b
¯
θ
˙
b
θσ
ν
¯
θ = (σ
μ
)
a
˙
b
¯
θ
˙
b
θ
c
(σ
ν
)
c
˙
d
¯
θ
˙
d
This can be rewritten in a more convenient form following the steps
(σ
μ
)
a
˙
b
¯
θ
˙
b
θ
c
(σ
ν
)
c
˙
d
¯
θ
˙
d
=−(σ
μ
)
a
˙
b
θ
c
(σ
ν
)
c
˙
d
¯
θ
˙
b
¯
θ
˙
d
=−
1
2
˙
b
˙
d
(σ
μ
)
a
˙
b
θ
c
(σ
ν
)
c
˙
d
¯
θ ·
¯
θ [using Eq. (A.48)]
=−
1
2
˙
b
˙
d
ce
(σ
μ
)
a
˙
b
θ
e
(σ
ν
)
c
˙
d
¯
θ ·
¯
θ(writing θ
c
=
ce
θ
e
)
=
1
2
(σ
μ
)
a
˙
b
( ¯σ
ν
)
˙
be
θ
e
¯
θ ·
¯
θ [using
ce
=−
ec
and
then Eq. (A.26)]
=
1
2
(σ
μ
¯σ
ν
)
b
a
θ
b
¯
θ ·
¯
θ
(13.35)

312
Supersymmetry Demystified
where we have relabeled e → b in the last step. Using again Eq. (A.48), we can
also prove
(σ
μ
)
a
˙
b
¯
θ
˙
b
(∂
μ
¯
λ) ·
¯
θ = (σ
μ
)
a
˙
b
¯
θ
˙
b
(∂
μ
¯
λ)
˙c
¯
θ
˙c
=−(σ
μ
)
a
˙
b
(∂
μ
¯
λ)
˙c
¯
θ
˙
b
¯
θ
˙c
=−
1
2
˙
b˙c
(σ
μ
)
a
˙
b
(∂
μ
¯
λ)
˙c
¯
θ ·
¯
θ
=−
1
2
(σ
μ
)
a
˙
b
(∂
μ
¯
λ)
˙
b
¯
θ ·
¯
θ (13.36)
Substituting Eqs. (13.35) and (13.36) into Eq. (13.33) and dropping the two terms
that contain only one
¯
θ (which won’t survive the application of
¯
D ·
¯
D), we get
D
a
V =
i
4
θ
a
¯
θ ·
¯
θ∂
μ
A
μ
+
1
2
√
2
¯
θ ·
¯
θλ
a
−
1
4
θ
a
¯
θ ·
¯
θ D
−
i
4
(σ
μ
¯σ
ν
)
b
a
θ
b
¯
θ ·
¯
θ∂
μ
A
ν
+
i
4
√
2
θ ·θ(σ
μ
)
a
˙
b
¯
θ ·
¯
θ
∂
μ
¯
λ
˙
b
(13.37)
This can be simplified even further. Recall that
σ
μν
≡
i
4
(σ
μ
¯σ
ν
− σ
ν
¯σ
μ
)
Using Eq. (A.9), this also may be written as
σ
μν
=
i
2
(σ
μ
¯σ
ν
− η
μν
1)
which implies
(σ
μ
¯σ
ν
)
b
a
= δ
b
a
η
μν
− 2 i (σ
μν
)
b
a
Using this in Eq. (13.37), we obtain a simple result:
D
a
V =
1
2
√
2
λ
a
−
1
4
θ
a
D −
1
2
(σ
μν
)
b
a
θ
b
∂
μ
A
ν
+
i
4
√
2
θ ·θ(σ
μ
)
a
˙
b
(∂
μ
¯
λ
˙
b
)
¯
θ ·
¯
θ

CHAPTER 13 Gauge Field Theories
313
All we now need is (see Exercise 13.1)
¯
D ·
¯
D
¯
θ ·
¯
θ = 4 (13.38)
which gives us
F
a
=
¯
D ·
¯
DD
a
V =
√
2 λ
a
− θ
a
D − 2 (σ
μν
)
b
a
θ
b
∂
μ
A
ν
+
i
√
2
θ ·θ(σ
μ
)
a
˙
b
(∂
μ
¯
λ
˙
b
)
Using the antisymmetry of σ
μν
in its Lorentz indices, we may write
σ
μν
∂
μ
A
ν
=
1
2
(σ
μν
− σ
νμ
)∂
μ
A
ν
=
1
2
σ
μν
(∂
μ
A
ν
− ∂
ν
A
μ
)
=
1
2
σ
μν
F
μν
(13.39)
Using this, and showing explicitly the y dependence of the fields, we obtain our
final result:
F
a
(y) =
√
2 λ
a
(y) − D(y)θ
a
− F
μν
(y)(σ
μν
)
b
a
θ
b
+
i
√
2
θ ·θ(σ
μ
)
a
˙
b
∂
μ
¯
λ
˙
b
(y)
(13.40)
At this point, we could rewrite the fields in terms of the spacetime coordinate x
using Eq. (12.3), but this won’t be necessary because we are ultimately interested
in the F term of F
a
F
a
, in which we may simply set y equal to x [see Eq. (12.27)].
EXERCISE 13.1
Prove Eq. (13.38).
13.5 The Free Abelian Supersymmetric
Lagrangian from the
Superfield Approach
We are finally ready to construct the lagrangian for the free abelian gauge theory in
the superfield approach. In sharp contrast with the usual field strength F
μν
, which is
a second-rank antisymmetric tensor (in other words, the coefficient of a two-form),

314
Supersymmetry Demystified
its supersymmetric extension is a spinor superfield. A lagrangian must be a Lorentz
scalar, so the obvious thing to consider is F
a
F
a
. Recall that F
a
is a left-chiral
superfield, so to obtain a supersymmetric lagrangian, we will need to extract its F
term. But let’s first start with the calculation of
F
a
F
a
=
ab
F
b
F
a
To alleviate the notation, we will not write explicitly that the fields depend on y,
but this must be kept in mind.
Since we are ultimately interested in taking the F term of this expression, we
need only retain the terms that contain two θ. These are
F
a
F
a
= 2 i θ ·θλσ
μ
∂
μ
¯
λ + D
2
θ ·θ +
ab
F
μν
(σ
μν
)
c
b
θ
c
F
αβ
(σ
αβ
)
d
a
θ
d
+···
(13.41)
where the dots indicate terms that will not contribute to the F term (to eliminate the
term containing D∂
μ
A
ν
, we have used the fact that
ab
θ
a
θ
c
(σ
μν
)
c
a
may be written
as θ ·θ Tr(σ
μν
)/2 which is identically zero). In order to read off the F term, it is
preferable to have all the θ combined in the form θ · θ . We can do this for the the
third term by using the identity (A.45):
ab
F
μν
(σ
μν
)
c
b
θ
c
F
αβ
(σ
αβ
)
d
a
θ
d
=
1
2
θ ·θ
ab
cd
F
μν
(σ
μν
)
c
b
F
αβ
(σ
αβ
)
d
a
(13.42)
Following the same steps as in part b of Exercise 6.5, it is straightforward to
prove
ab
cd
(σ
μν
)
c
b
=−(σ
μν
)
a
d
so that Eq. (13.42) becomes
1
2
ab
cd
θ ·θ(σ
μν
)
c
b
F
μν
(σ
αβ
)
d
a
F
αβ
=−
1
2
θ ·θ(σ
μν
)
a
d
F
μν
(σ
αβ
)
d
a
F
αβ
=−
1
2
θ ·θ Tr
σ
μν
σ
αβ
F
μν
F
αβ
(13.43)
To make progress on this term, the following identity is required
Tr
σ
μ
¯σ
ν
σ
α
¯σ
β
= 2
η
μν
η
αβ
+ η
να
η
μβ
− η
μα
η
νβ
−i
μναβ
(13.44)
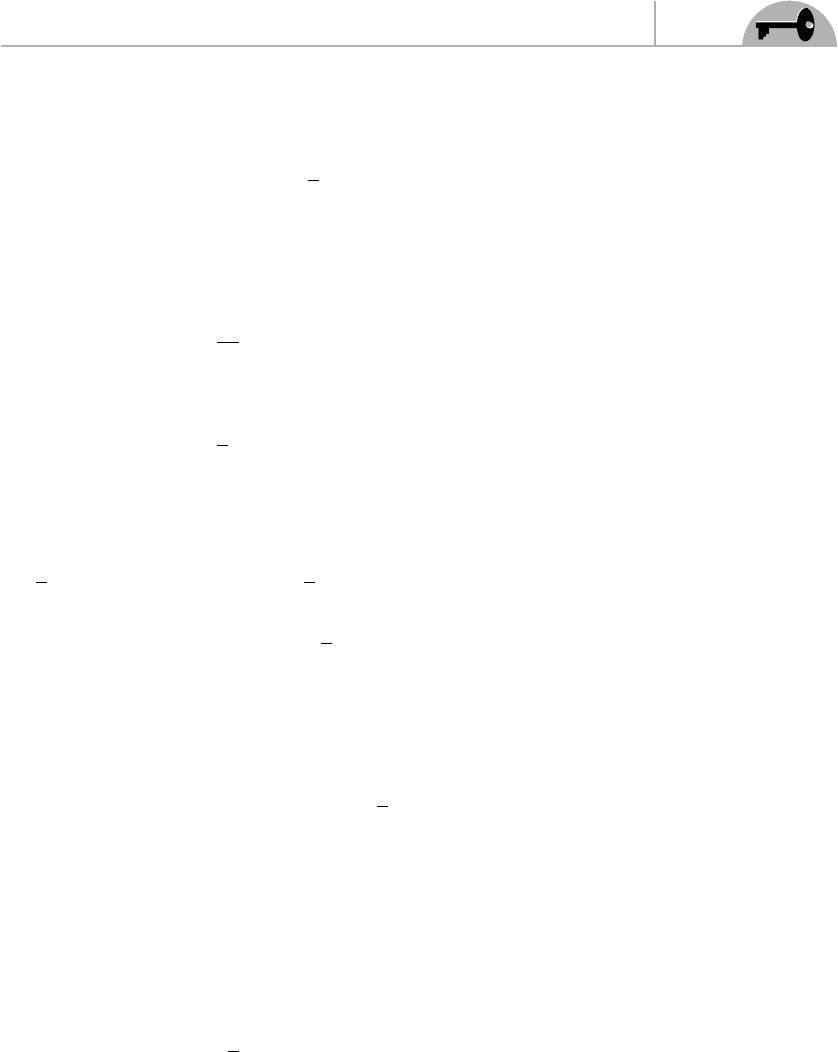
CHAPTER 13 Gauge Field Theories
315
Using the definition
σ
μν
=
i
4
σ
μ
¯σ
ν
− σ
ν
¯σ
μ
and the corresponding expression for σ
αβ
, and applying Eq. (13.44), a short calcu-
lation reveals that
Tr
σ
μν
σ
αβ
=−
1
16
Tr
σ
μ
¯σ
ν
σ
α
¯σ
β
− σ
μ
¯σ
ν
σ
β
¯σ
α
− σ
ν
¯σ
μ
σ
α
¯σ
β
+σ
ν
¯σ
μ
σ
β
¯σ
α
=−
1
2
η
να
η
μβ
− η
μα
η
νβ
−i
μναβ
(13.45)
Plugging this into Eq. (13.43), we get
−
1
2
θ ·θ Tr
σ
μν
σ
αβ
F
μν
F
αβ
=
1
4
θ ·θ
F
μν
F
νμ
− F
μν
F
μν
−i
μναβ
F
μν
F
αβ
=−
1
4
θ ·θ
2F
μν
F
μν
+i
μναβ
F
μν
F
αβ
(13.46)
where we have used the antisymmetry of the field strength, i.e., F
νμ
=−F
μν
.
Using Eq. (13.46) for the third term of Eq. (13.41), we finally get
F
a
F
a
= 2 i θ ·θλσ
μ
∂
μ
¯
λ + D
2
θ ·θ −
1
4
θ ·θ
2F
μν
F
μν
+i
μναβ
F
μν
F
αβ
Recall that all the fields are functions of the variable y. However, if we extract the
F term, i.e., the coefficient of θ ·θ/2, we may replace y by x, as you have shown
in Exercise 12.1. We then get
F
a
F
a
F
= 4 i λ(x)σ
μ
∂
μ
¯
λ(x) + 2 D
2
(x) − F
μν
(x) F
μν
(x)
−
i
2
μναβ
F
μν
(x) F
αβ
(x)
This is starting to resemble the lagrangian of the supersymmetric free abelian gauge
theory, [Eq. (10.8)]. The kinetic term for the spinor looks different, but looks can
