Labelle P. Supersymmetry DeMYSTiFied

Подождите немного. Документ загружается.

116

Supersymmetry Demystified

transformations therefore is given by

= exp(iQ·ζ + i

Q ·

ζ) (6.51)

If we apply Eq. (6.12) to the SUSY transformations of φ and χ given in Eq.

(5.17), we get

[ζ · Q +

ζ ·

Q,φ] =−iζ · χ

[ζ · Q +

ζ ·

Q,χ] =−i(∂

φ) σ

∗

which implies

[ζ · Q,φ] =−iζ · χ

[

ζ ·

Q,χ] =−i(∂

φ) σ

∗

[

ζ ·

Q,φ] = [ζ · Q,χ] = 0 (6.52)

We now consider two successive SUSY transformations of the ﬁelds in order to

use Eq. (6.40). We will use β as the inﬁnitesimal parameter of the second transfor-

mation. Therefore, the ﬁrst transformation is generated by the operator (6.51), and

the second transformation is generated by

= exp(iQ·β +i

Q ·

β)

Let’s apply Eq. (6.40) to the scalar ﬁeld φ of our supersymmetric lagrangian (we

will consider the spinor ﬁeld χ later); we get

φ −δ

φ =



[Q · ζ +

Q ·

ζ, Q · β +

Q ·

β],φ





[Q · ζ, Q · β],φ





[Q · ζ,

Q ·

β],φ





[

Q ·

ζ, Q · β],φ





[

Q ·

ζ,

Q ·

β],φ



(6.53)

Right-Hand Side of Eq. (6.53)

The right-hand side of Eq. (6.53) can be brought into a much more useful form by

writing all the commutators of the charges with the inﬁnitesimal parameters factored

out (it will become clear shortly why this is a useful thing to do). Let’s consider the

CHAPTER 6 The Supersymmetric Charges

117

ﬁrst commutator, which we rewrite explicitly in terms of the components:

[Q · ζ, Q · β] =



Q (−iσ

)ζ,Q(−iσ

)β



=−



(σ

)

, Q

(σ

)



(6.54)

where it is understood that the whole expression is acting on the ﬁeld φ.

The indices on the σ

have been chosen so that the usual summation convention

of relativity is respected (if you have read Chapter 3, this should be familiar; if not,

don’t read too much into it, it’s just a convention and these σ

matrices will drop

out of our ﬁnal result anyway).

Now we have to be careful. The ζ

and β

are Grassmann numbers, but the Q

are Grassmann operators! Thus we can move the β

and ζ

through each other and

through the Q

on the condition of adding a minus sign, but we cannot switch the

order of the Q

(for the same reason that we cannot switch the order of

X and

P in

quantum mechanics). As for the components of the σ

, these are simple numbers,

so we can move them anywhere we wish with no fear. We therefore can write

−



(σ

)

, Q

(σ

)



=−(σ

)

(σ

)

− Q

)

= (σ

)

(σ

)

+ Q

)

= (σ

)

(σ

)

, Q

} (6.55)

Note that we started with a commutator of Q · ζ and Q · β but ended up with an

anticommutator of the charges. This is obviously due to the fermionic (Grassmann)

nature of the inﬁnitesimal parameters.

Equation (6.55) is a useful form because it is written explicitly in terms of the

anticommutator of the charges, which will make it easier for us to isolate them in

the next section.

We still have three commutators to work out in Eq. (6.53). Consider the second

one:

[Q · ζ,

Q ·

β] =



(−iσ

)

, Q

†

(iσ

)

∗





(σ

)

, Q

†

(σ

)

∗



If you have read Chapter 3, you know that, strictly speaking, we should be using

dotted indices on the second σ

, but again, this will not matter for the present

calculation. Now we can simply repeat the steps that led to Eq. (6.55) to get

[Q · ζ,

Q ·

β] =−(σ

)

(σ

)

∗

, Q

†

} (6.56)

118

Supersymmetry Demystified

The remaining two commutators of Eq. (6.53) are now just a repeat:

[

Q ·

ζ,Q ·β] =−(σ

)

(σ

)

∗

†

, Q

}

[

Q ·

ζ,

Q ·

β] = (σ

)

(σ

)

∗

†

, Q

†

} (6.57)

Putting it all together, we see that Eq. (6.53) may be written as

φ −δ

φ = [O,φ] (6.58)

with the operator O being given by the sum of Eqs. (6.55) and (6.56), and the two

expressions of Eq. (6.57)

O = (σ

)

(σ

)



, Q

}−ζ

∗

, Q

†

}

− ζ

∗

†

, Q

}+ζ

∗

†

, Q

†

}



(6.59)

Left-Hand Side of Eq. (6.53)

Using the SUSY transformations (5.17),weﬁnd

φ = δ

(−ζ

iσ

χ)

=−ζ

iσ

= ζ

iσ

∗

∂

=−iζ

∗

∂

=−iζ

¯σ

μT

∗

∂

φ using Eq. (A.5)

= iβ

†

¯σ

ζ∂

φ using Eq. (A.36) (6.60)

where we have used the fact that ∂

φ is not a matrix, so we are free to move it

around.

The last line in Eq. (6.60) is clearly the most condensed and most elegant way

to write the result, but the form shown two lines above (with the σ

still explicit)

will be more useful to compute the SUSY algebra because Eq. (6.59) contains σ

matrices too.

By switching β and ζ , we obviously have

φ =−iβ

∗

∂

= i ζ

†

¯σ

β∂

CHAPTER 6 The Supersymmetric Charges

119

Therefore, the left-hand side of Eq. (6.58) is equal to

φ −δ

φ =−i (ζ

∗

− β

∗

)∂

=−i(ζ

†

¯σ

β − β

†

¯σ

ζ)∂

φ (6.61)

Again, the ﬁrst form will be the one we will use to obtain the SUSY algebra, but

the second one is the most elegant (and will prove useful later on).

What we now have to do is to set this equal to the right-hand side of Eq. (6.58). In

order to be able to extract explicit expressions for the anticommutators of the SUSY

charges, we need to write Eq. (6.61) in the form of the commutator of something

with the scalar ﬁeld. The trick is simply to use Eq. (6.20), namely, ∂

φ = i [P

,φ],

which allows us to write the ﬁrst line of Eq. (6.61) as

φ −δ

φ =



∗

− β

∗



,φ







∗

− β

∗



,φ



(6.62)

where the last step is possible because ζ , β and the sigma matrices commute with φ.

Finally, comparing Eq. (6.62) with Eq. (6.58), we get

[O,φ] =



(ζ

∗

− β

∗

,φ



(6.63)

with O given by Eq. (6.59). It is tempting to conclude that this implies

O =



∗

− β

∗



(6.64)

but we have only proved Eq. (6.64) when the two sides are applied to the scalar

ﬁeld φ. Before concluding that it is a valid identity in our theory, we must prove

that it is also satisﬁed when applied to the spinor ﬁeld χ. It turns out, as we will

demonstrate in the next section, that Eq. (6.64) is not valid when applied to the

spinor ﬁeld. This will lead us to modify our lagrangian to ensure that Eq. (6.64)

does apply to all ﬁelds. Since the end result is that Eq. (6.64) will be satisﬁed, let’s

go ahead and use it to work out the SUSY algebra.

The right-hand side of Eq. (6.64) is not yet in a suitable form for comparison

with Eq. (6.59) because we still need to factor out the inﬁnitesimal parameters and

write explicit indices on everything. To facilitate the comparison, we will assign

the same indices to ζ and β as they have in Eq. (6.59), i.e., b for ζ and d for β.We

120

Supersymmetry Demystified

therefore write

∗

= ζ

(σ

)

(σ

)

(σ

)

∗

(6.65)

and

∗

= β

(σ

)

(σ

)

(σ

)

∗

(6.66)

Note that in Eq. (6.59) the indices of the two σ

matrices are, respectively, ab and

cd. We would like to have the same indices in our two σ

matrices in Eqs. (6.65) and

(6.66) because then we will be able to cancel them out in Eq. (6.64). This is easy to

achieve because σ

is antisymmetric, so (σ

)

=−(σ

)

and (σ

)

=−(σ

)

In addition, we will move the ζ

∗

to the left of the β

in Eq. (6.66) because this is

the order in which these appear in Eq. (6.59). Using the fact that the components of

the σ matrices are simply numbers that can be moved around freely, we can rewrite

Eq. (6.65) as

∗

=−ζ

∗

(σ

)

(σ

)

(σ

)

(6.67)

and Eq. (6.66) as

∗

= ζ

∗

(σ

)

(σ

)

(σ

)

Using these last two results in Eq. (6.64), we obtain

O =−(σ

)

(σ

)



∗

(σ

)

+ ζ

∗

(σ

)



(6.68)

Using Eq. (6.59) for O and canceling out the components (σ

)

(σ

)

appearing

on both sides, we ﬁnally get

, Q

}−ζ

∗

, Q

†

}−ζ

∗

†

, Q

}+ζ

∗

†

, Q

†

}

=−ζ

∗

(σ

)

− ζ

∗

(σ

)

(6.69)

Since the spinors ζ,β and their complex conjugates are arbitrary, Eq. (6.69)

actually contains four independent equations. The terms in ζ

and in ζ

∗

lead to

, Q

}=0 (6.70)

CHAPTER 6 The Supersymmetric Charges

121

and

†

, Q

†

}=0 (6.71)

If you have read Chapter 3, you know that using the dotted and bar notation, this

also can be written as

{

˙a

}=0

Now, if we consider the terms in ζ

∗

in Eq. (6.69), we ﬁnd

, Q

†

}=(σ

)

which is usually written with the index on Q

†

labeled b:

, Q

†

}=(σ

)

(6.72)

Again, using the bar and dotted notation of Chapter 3, this may be written as

}=(σ

)

(6.73)

It is important to point out that the normalization of the supercharges is arbitrary,

so we are free to rescale Eqs. (6.72) and (6.73) by a constant. Another way to

put it is that we could have multiplied the supercharges in the exponential of U

by an arbitrary factor. A normalization that is used often in the SUSY literature

corresponds to rescaling our supercharges by Q → Q/

√

2, which then transforms

Eqs. (6.72) and (6.73) into

, Q

†

}=2(σ

)

}=2(σ

)

(6.74)

We will use the normalization Eq. (6.72).

Let’s ﬁnish with the terms in ζ

∗

in Eq. (6.69). These yield the relation

†

, Q

}=(σ

)

(6.75)

It is easy to see, however, that this is equivalent to Eq. (6.72). By the deﬁnition of

an anticommutator, we may exchange Q

†

and Q

(without picking up any minus

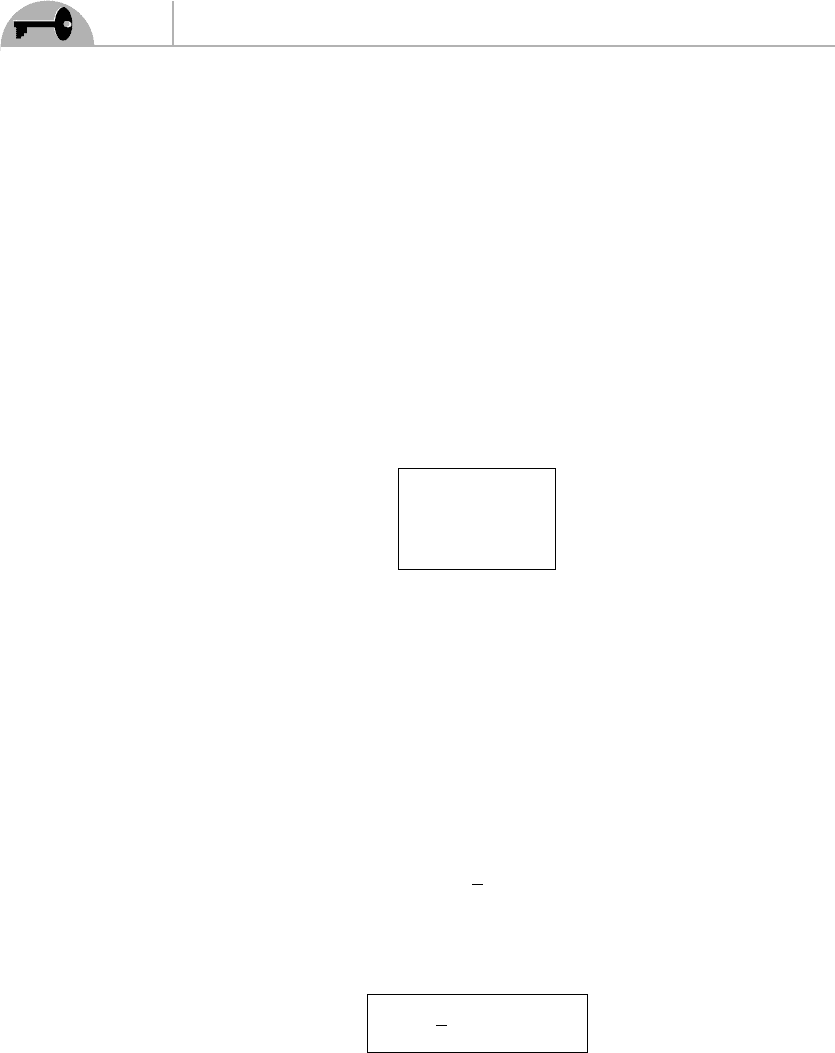
122

Supersymmetry Demystified

sign) and write Eq. (6.75) as

, Q

†

}=(σ

)

which, after renaming the indices, is exactly the same as Eq. (6.72).

The commutation relations (6.70), (6.71), and (6.72) are what we were seeking:

the algebra of the SUSY charges. The fact that the anticommutators (6.72) contain

the four-momentum operator is a crucial aspect of supersymmetry, and we will

discuss this in more detail shortly.

To complete the algebra, we need to work out the commutators of the SUSY

charges with the Poincar´e generators P

and M

μν

. It is easy to see that the super-

charges commute with the momentum operator because the SUSY transformations

do not generate any function of x on which the derivatives of P could act, so



, P



= 0



†

, P



= 0

(6.76)

Things are a bit more interesting when it comes to the commutator with the

Lorentz generators M

μν

. To work this out, we ﬁrst need to write down the Lorentz

transformation of Weyl spinors. The Lorentz transformation of a spinor ﬁeld has

two contributions: The argument transforms in the same way as for a scalar ﬁeld

[see Eq. (6.23)], but in addition, the spinor gets multiplied by the matrices shown

in Eq. (2.32).

Our ﬁrst step is to write down a covariant expression for the transformation of

the spinors given in Eq. (2.32) in terms of the parameters ω

μν

. For a left-chiral Weyl

spinor, the answer is that Eq. (2.32) may be written as



= exp



μν



χ (6.77)

where the matrices σ

μν

are deﬁned as

μν

≡

(σ

¯σ

− σ

¯σ

) (6.78)

Note that σ

μν

is antisymmetric under the exchange of the indices μ and ν. The

exponential can be shown to reproduce the transformation of χ given in Eq. (2.32),

with an appropriate choice of the coefﬁcients ω

μν

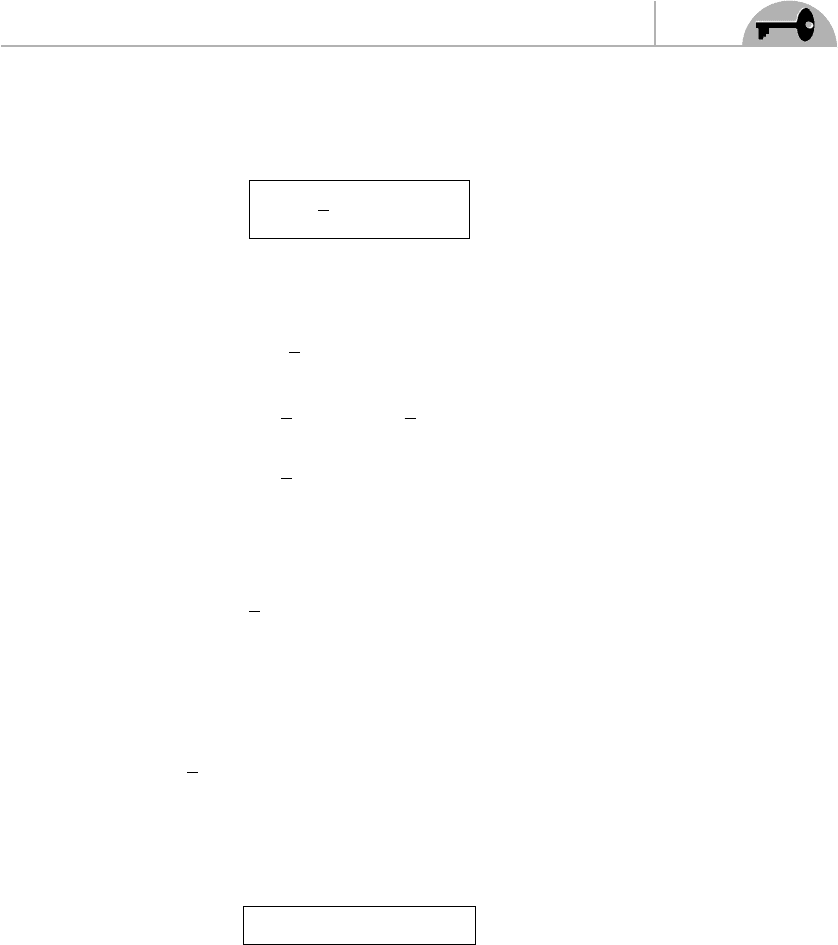
CHAPTER 6 The Supersymmetric Charges

123

As for a right-chiral spinor η, it transforms as in Eq. (6.77) but with σ

μν

replaced

¯σ

μν

≡

( ¯σ

− ¯σ

) (6.79)

The complete Lorentz transformation of a left-chiral spinor therefore is

χ → χ



(x) = exp



μν



χ(x

+ ω

μν

)

≈ χ +

μν

χ +

μν



∂

χ − x

∂



= χ +

μν



iσ

μν

χ + x

∂

χ − x

∂



(6.80)

so the variation of the spinor is given by

χ =

μν



iσ

μν

χ + x

∂

χ − x

∂



(6.81)

To work out the commutation relation of the supercharges Q

with the Lorentz

generators M

μν

, we start again from Eq. (6.40), which now takes the form

−



[ζ · Q,ω

μν

],φ



= δ

φ −δ

φ (6.82)

where the factor of −1/2 is the one that accompanies the generators M

μν

(see

Exercise 6.1). It is then a simple matter to show that

, M

μν

] = (σ

μν

)

(6.83)

the proof of which is the subject of Exercise 6.5. The indices of σ

μν

are chosen

this way in order to satisfy the usual summation convention. The matrices σ

μν

are

antisymmetric, which is why we need to use spaces to indicate clearly that the upper

index is the second index.

The only tricky aspect of the derivation is that we need at some point the com-

mutator of the supercharges with the scalar ﬁeld. This is easy to ﬁnd by going back

to Eq. (6.12), which, using the SUSY transformation of the scalar ﬁeld δφ = ζ · χ,

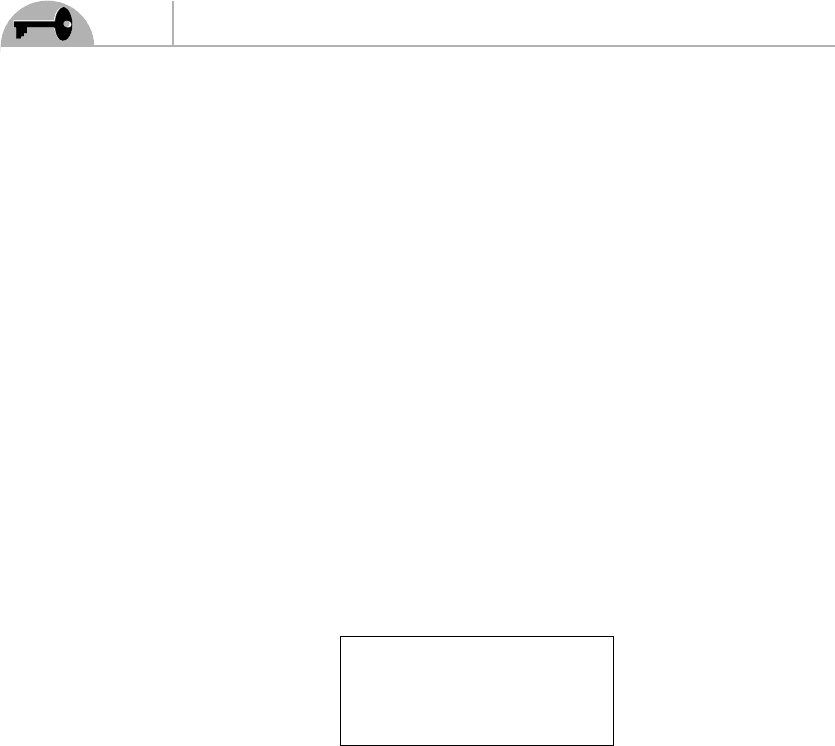
124

Supersymmetry Demystified

becomes

[ζ · Q,φ] =−iζ · χ (6.84)

This immediately gives us

,φ] =−iχ

or, suppressing the spinor indices,

[Q,φ] =−iχ (6.85)

Using this result, it is a simple matter to prove Eq. (6.83) starting from Eq. (6.82).

This calculation is the object of the ﬁrst part of Exercise 6.5.

The calculation of the commutation relation with the charges Q

†

and Q

a†

much simpler using the van der Waerden notation of Chapter 3. We will simply

quote the result and leave the derivation to the second part of Exercise 6.5. If you

haven’t covered Chapter 3 yet, you may skip this exercise for now and come back

to it later. The ﬁnal results are



˙a

, M

μν



=−

( ¯σ

μν

)

˙a



˙a

, M

μν



= ( ¯σ

μν

)

˙a

(6.86)

We have achieved our goal of obtaining the complete algebra of the supercharges.

However, as mentioned earlier, we have cheated in the step from Eq. (6.63) to Eq.

(6.64) because we have not shown that Eq. (6.64) was valid when applied to the

spinor ﬁeld as well as to the scalar ﬁeld. We will remedy this lapse in the next

section.

EXERCISE 6.5

a. Prove the commutation relation (6.83).

b. Prove Eq. (6.86) to be done after you have gone through Chapter 3.

Hint: In order to get an expression for the supercharges

Q, which are related to

the hermitian conjugates of the supercharges Q, we use Eq. (6.40), but with the

transformations on the left side applied to φ

†

instead of φ. So the starting point

CHAPTER 6 The Supersymmetric Charges

125

will be

−



[

Q ·

ζ,ω

μν

],φ

†



= δ

†

− δ

†

(6.87)

It will then be straightforward to prove the ﬁrst commutator of Eq. (6.86). You can

then use  symbols to obtain the second commutator from the ﬁrst. You will need

to show that



˙c



d ˙a

( ¯σ

μν

)

˙a

= ( ¯σ

μν

)

˙c

(6.88)

6.6 Nonclosure of the Algebra for

the Spinor Field

As mentioned earlier, the SUSY algebra we have just obtained is, strictly speaking,

valid only when applied to the scalar ﬁeld. To prove that the algebra is valid in

general, we have to check if we would have obtained the same result starting from

the transformation of the spinor ﬁeld. We will now see that it will not work without

modifying the theory in a nontrivial way.

Consider the variation of the spinor ﬁeld. Using Eq. (5.17), we get

χ = δ

(−iσ

iσ

∗

∂

φ)

= (σ

∗

)∂

(δ

φ)

= (σ

∗

)β·∂

where, obviously, β · ∂

χ stands for the usual spinor dot product between β and

∂

χ:

β · ∂

χ = β

(−iσ

)∂

Note that what we have is really two identities, one for each component of χ .To

make this more clear, we can write

= (σ

∗

)

β · ∂

χ (6.89)