Кузюрин Н.Н. Фомин С.А. Эффективные алгоритмы и сложность вычислений

Подождите немного. Документ загружается.

6.3. Вероятностные вычисления 251

Теорема 6.3.5. «Закон Больших Чисел для схемы Бернулли»

Пусть событие A может произойти в любом из t незави-

симых испытаний с одной и той же вероятностью p, и пусть

— число осуществлений события A в t испытаниях. Тогда

7−→ p, причем для любого ε > 0:





− p



≥ ε



≤

p(1 − p)

tε

Теорема 6.3.6. «Оценка Чернова» (Chernoﬀ bounds).

Пусть M

, . . . , M

— независимые события, каждое из ко-

торых имеет вероятность p ≥

. Тогда вероятность одновре-

менного выполнения более половины событий будет больше,

чем 1 − exp(−2(p −

)

t).

Лемма 6.3.7. BPP

weak

= BPP.

Доказательство. Очевидно, что BPP ⊆ BPP

weak

, для этого

достаточно положить c ≡

и p(|x|) ≡ 6.

Теперь покажем BPP

weak

⊆ BPP. Пусть L ∈ BPP

weak

обозначим через M

weak

ВМТ из определения 6.3.11, построим

M из определения 6.3.10 «BPP».

На входе x машина M вычислит p(|x|), затем будет за-

пускать t = 6p

(|x|) раз машину M

weak

(обозначим ре-

зультат i-го запуска через M

weak

) и возвращать «1», если

i=1

weak

> t · c, или «0» в противном случае.

Рассмотрим P

err

= P(M(x) = 0|x ∈ L) — вероятность ошиб-

ки первого рода:

err

= P[M

< t · c].

Заметим, что при x ∈ L мат. ожидание «суммарного голосова-

ния» машин M

weak

будет

E M

(x) = t · E



weak

(x)



≥ t ·



c +

p(|x|)



252 Глава 6. Основы теории сложности вычислений

откуда, применяя теорему 6.3.5 и учитывая, что 0 ≤

E(M

)

≤ 1,

получаем

err

≤ P





−

E(M

)



≥

p(|x|)



≤

(|x|)

≤

Вероятность ошибки второго рода P

err

= P(M(x) = 1|x /∈ L)

оценивается аналогично.

Лемма 6.3.8. BPP

strong

= BPP.

Доказательство. Очевидно, что BPP

strong

⊆ BPP, оста-

лось показать обратное вложение. Действуем аналогично лем-

ме 6.3.7, строим машину M

strong

, запуская t = 2p(|x|) + 1 раз

(пусть будет нечетное число) обычную BPP-машину M и при-

нимая решения на основе «большинства» ее результатов. Если

x ∈ L, то, согласно теореме 6.3.6, вероятность правильного

ответа:

P(M

strong

(x) = 1) ≥ 1 − exp

−2



p −



· t

= 1 − exp

−2



−



· (2p(|x|) + 1)

= 1 − exp



−

2p(|x|) + 1



> 1 − e

−

p(|x|)

> 1 − 2

−p(|x|)

Упражнение 6.3.1. Вы разработчик военного программно-

го комплекса, использующего сложновычислимую и секретную

функцию F : [0, . . . , N − 1] → [0, . . . , m − 1], которую подклю-

чают к вашему алгоритму в виде отдельного массива длины N,

т. е. функция задана таблично на внешней флеш-памяти огром-

ного объема(только вес этой флэшки — 20 кг, которую носят и

охраняют два майора-особиста). Функция гомоморфна, т. е.

F ((x + y) mod N) = (F (x) + F (y)) mod m

6.3. Вероятностные вычисления 253

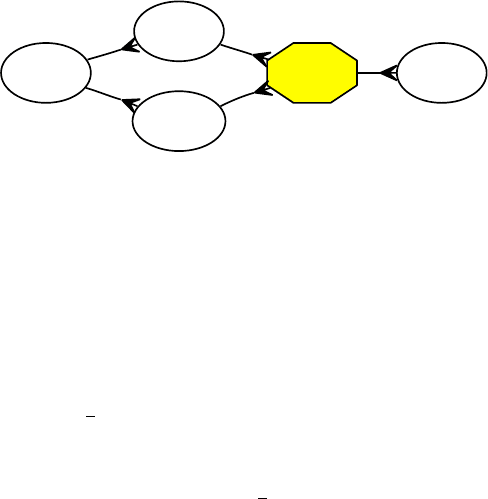
Стрелки показывают вложенность классов сложности

Ð²

coRP

Ð²

BPP PP

Ð²

Рис. 6.12. Классы сложности: BPP и его «соседи»

Однако, утром перед приемными испытаниями, выясни-

лось, что «флешка побилась», т. е. некоторые значения этой

функции стали неверными. Виновные майоры уже расстреля-

ны, а вся команда разработчиков пытается решить проблему.

Инженеры исследовали сбой — и утверждают, что «поби-

лось» не более

ячеек, к сожалению, неизвестно каких.

С учетом этого факта вам поставлена задача реализовать

простой и быстрый алгоритм, который правильно вычисляет

F (x) с вероятностью не меньше

Упражнение 6.3.2. Все то же, что и в упражнении 6.3.1, но

чтобы вероятность ошибки P

err

можно было сделать произ-

вольно малой, т. е. 2

−p(|x|)

, и при этом, чтобы выполнение ал-

горитма было замедлено не больше, чем в O(p(|x|)) раз.

Упражнение 6.3.3. Вводная, что и в упражнении 6.3.1, толь-

ко теперь достаточно времени (испытания прошли, есть пара

недель перед вводом в опытную эксплуатацию), и нужно вос-

становить значение этой функции за время O(N

6.3.3. Класс PP

Теперь познакомимся с максимально широким классом языков,

распознаваемых полиномиальной ВМТ.

254 Глава 6. Основы теории сложности вычислений

Определение 6.3.13. Класс сложности PP (Probability

Polynomial-time) состоит из всех языков L, для которых су-

ществует полиномиальная ВМТ M, такая, что:

x ∈ L ⇒ P [M(x) = 1] >

x /∈ L ⇒ P [M(x) = 0] >

По опыту разделов 6.3.1 и 6.3.2 читатель может пред-

положить, что константа «

» также выбрана произвольно,

«для красоты», но здесь это не так. В отличие от определе-

ний 6.3.3 «RP», 6.3.10 «BPP», в определении 6.3.13 «PP» мы

никак не можем заменить константу «

» на любую большую

константу, т.к. в этом случае нет гарантированной возможно-

сти амплификации вероятности за полиномиальное время.

Обратите внимание, что в определении 6.3.13 «PP» важна

даже строгость неравенства (что необязательно для определе-

ний 6.3.3 «RP», 6.3.10 «BPP»), т. е. нельзя заменить символ

«>» на «≥», т.к. тогда определение полностью «выродится»,

ведь проверяющую машину можно будет заменить подбрасы-

ванием одной монетки. Единственное ослабление, на которое

мы можем пойти, — это пожертвовать строгостью одного из

неравенств в определении.

Определение 6.3.14. Класс сложности PP

weak

состоит

из всех языков L, для которых существует полиномиальная

ВМТ M, такая, что:

x ∈ L ⇒ P [M(x) = 1] >

x /∈ L ⇒ P [M(x) = 0] ≥

Упражнение 6.3.4. Что будет, если в определении 6.3.14

в обоих неравенствах поставить «≥»? Какой класс языков бу-

дет определен?

6.3. Вероятностные вычисления 255

Лемма 6.3.9. PP

weak

= PP.

Доказательство. Очевидно, доказывать нужно только вложе-

ние PP

weak

⊆ PP, для чего мы покажем, как для любого

языка L ∈ PP

weak

из машины M

weak

(машина M из опреде-

ления 6.3.14) сделать машину M из определения 6.3.13 «PP».

Пусть машина M

weak

использует не больше w(|x|) случайных

бит (см. определение 6.3.2 «oﬀline ВМТ»), машина M будет ис-

пользовать p(|x|) = 2 · w(|x|) + 1 случайных бит следующим

образом:

M(x,hr

, ...,r

p(|x|)

i)≡(r

w(|x|)+1

∨ ...∨r

p(|x|)

)∧M

weak

(x,hr

, ...,r

w(|x|)

i),

причем, «оптимизируя» вычисление этого выражения, мы да-

же не будем запускать M

weak

, если r

w(|x|)+1

∨ . . . ∨ r

p(|x|)

= 0,

что, очевидно, может произойти с вероятностью 2

−(w(|x|)+1)

Итак, рассмотрим случай x ∈ L. Тогда P(M

weak

(x) = 1) >

причем P(M

weak

(x) = 1) ≥

−w(|x|)

, т.к. всего вероятностных

строк не больше 2

w(|x|)

, и минимальный «квант» вероятности,

соответствующий одной вероятностной строке, будет не мень-

ше 2

−w(|x|)

P(M(x) = 1) =



1 − 2

−(w(|x|)+1)



· P (M

weak

(x) = 1) ≥

≥



1 − 2

−(w(|x|)+1)





+ 2

−w(|x|)



+ 2

−(w(|x|)+1)



− 2

−w(|x|)



Если x /∈ L, то P(M

weak

(x) = 0) ≥

, а

P(M(x) = 0) =



1 − 2

−(w(|x|)+1)



· P(M

weak

(x) = 0)+

+ 2

−(w(|x|)+1)

≥



1 − 2

−(w(|x|)+1)



+ 2

−(w(|x|)+1)

256 Глава 6. Основы теории сложности вычислений

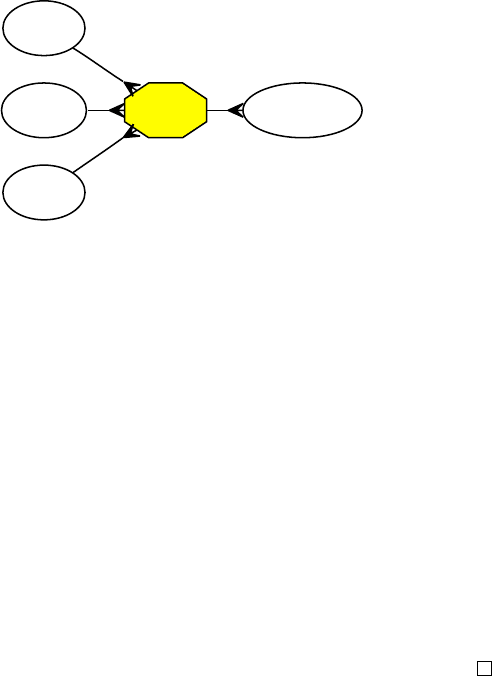
Стрелки показывают вложенность классов сложности

Ð²

coNP

Ð²

BPP

Ð²

PSPACE

Ð²

Рис. 6.13. Классы сложности: PP и его «соседи»

Исследуем отношение класса PP к известным нам классам

сложности.

Теорема 6.3.10. PP ⊆ PSPACE.

Доказательство. Для любого языка L ∈ PP из машины M

(машина M из определения 6.3.13 «PP») можно сделать ма-

шину M, которая последовательно запускает M

на x и всех

p(|x|)

возможных вероятностных строках, и результат опреде-

ляется по большинству результатов запусков. Машина M будет

разрешать язык L и использовать не более полинома ячеек на

ленте, т.к. каждый запуск M

может использовать один и тот

же полиномиальный отрезок ленты.

Теорема 6.3.11. N P ⊆ PP.

Доказательство. Покажем, как для любого языка L ∈ N P из

машины M

(машина M из определения 6.2.4 «N P/ДМТ»)

сделать машину M из определения 6.3.14. Пусть размер под-

сказки y для машины M

ограничен полиномом p(|x|). Тогда

6.3. Вероятностные вычисления 257

машина M будет использовать p(|x|) + 1 случайных бит следу-

ющим образом:

M(x, hr

, . . . , r

p(|x|)+1

i) ≡ r

p(|x|)+1

∨ M

(x, hr

, . . . , r

p(|x|)

i).

При x ∈ L, P(M(x) = 1) =

+ 2

−p(|x|)

. При x /∈ L,

P(M(x) = 0) =

. Таким образом, учитывая лемму 6.3.9, по-

лучаем L ∈ PP

weak

= PP.

Аналогично получаем следующую лемму.

Лемма 6.3.12. coN P ⊆ PP.

6.3.4. Класс ZPP.



Алгоритмы без ошибок



Пока в разделах 6.3.1, 6.3.2 и 6.3.3 мы рассматривали «ошиба-

ющиеся» вероятностные алгоритмы распознавания. Еще один

интересный класс вероятностных алгоритмов распознавания —

алгоритмы, которым в дополнение к стандартным ответам «0»

и «1» разрешено выдавать неопределенный ответ «?». Ответ

«?» означает «не знаю» и не считается ошибочным в любом

случае. Используя эти алгоритмы, мы можем определить еще

один класс языков.

Определение 6.3.15. Класс сложности ZPP состоит из

всех языков L, для которых существует полиномиальная

ВМТ M, возвращающая только ответы «0»,«1»,«?» («не

знаю»), причем:

x ∈ L ⇒ P [M(x) = 1] >

∧ P [M(x) = 1] + P [M(x) = «?»] = 1,

x /∈ L ⇒ P [M(x) = 0] >

∧ P [M(x) = 0] + P [M(x) = «?»] = 1.

Оказывается, у этого класса есть и альтернативное опреде-

ление:

Теорема 6.3.13. ZPP = RP ∩ coRP.

258 Глава 6. Основы теории сложности вычислений

Доказательство. ZPP ⊆ RP, т.к. для любого языка L ∈ ZPP

из машины M

ZPP

(машина M из определения 6.3.15 «ZPP»)

можно сделать машину M из определения 6.3.3 «RP»:

Answer = M

ZPP

(x)

if Answer = «?» then

Answer = 0

end if

RETURN Answer

Действительно, если x ∈ L, то P [M

ZPP

(x) = 1] >

, и, следова-

тельно, P [M(x) = 1] ≥

. Если x /∈ L, то

P [M(x) = 0] = P [M

ZPP

(x) = 0] + P [M

ZPP

(x) = «?»] = 1.

Аналогично доказывается, что ZPP ⊆ coRP.

Теперь покажем, что RP ∩ coRP ⊆ ZPP. Изготовим ма-

шину M для распознавания ZPP из машин M

(M из опреде-

ления 6.3.3 «RP») и M

coRP

(M из определения 6.3.4 «coRP»),

используя «безошибочные» возможности обеих машин:

if M

(x) = 1 then

RETURN «1»

end if

if M

coRP

(x) = 0 then

RETURN «0»

end if

RETURN «?»

Итак, кратко напомним отношения между уже знакомыми

и новыми вероятностными классами сложности, определенны-

ми в этом разделе, на рис. 6.14, где стрелками отображаются

отношения вложенности.

6.3. Вероятностные вычисления 259

P ZPP

Ð²

coNP

Ð²

BPP

Ð²

coRP

Ð²

PSPACE

Ð²

Рис. 6.14. Вероятностные классы сложности: ZPP, RP, BPP, ZPP

Упражнение 6.3.5. Класс сложности ZPP

NotNull

состоит из

всех языков L, для которых существует ВМТ M, всегда возвра-

щающая правильные ответы (т. е. никаких «не знаю»), причем

∃ полином p(n), что для времени работы T

(x) машины M вы-

полняется:

E T

(x) ≤ p(|x|).

Докажите, что ZPP

NotNull

= ZPP.

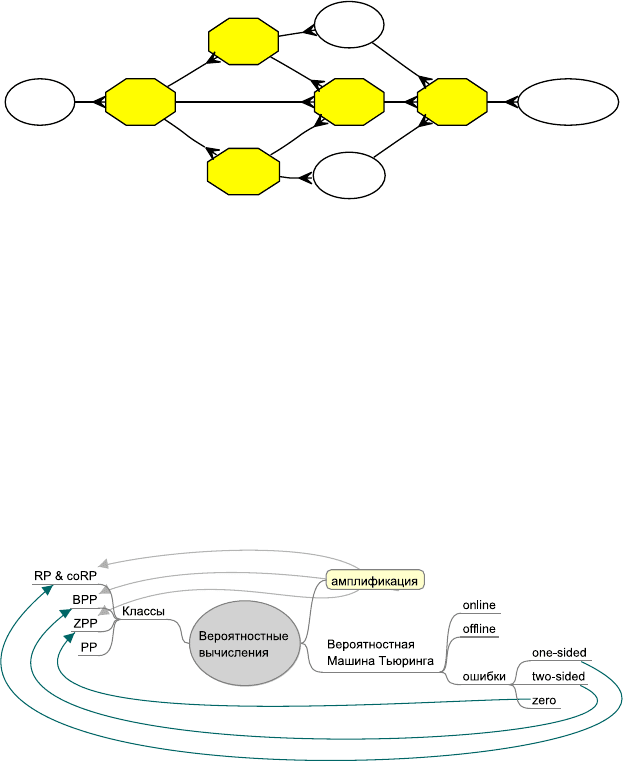
Рис. 6.15. Карта-памятка раздела 6.3

6.3.5. Вероятностно проверяемые доказательства

К середине 1990-х годов было доказано, что для многих за-

дач полиномиальных алгоритмов с лучшими, чем известные,

260 Глава 6. Основы теории сложности вычислений

оценками точности не существует при стандартной гипотезе

P 6= N P (или сходных с ней). Результат, который позволил

доказывать подобные теоремы, — одно из самых ярких дости-

жений теории сложности. Он получил название PCP-теоремы

(Probabilistically Checkable Proofs).

Эта теорема устанавливает неожиданную связь между ин-

терактивными доказательствами и приближенными алгорит-

мами. Как мы уже говорили, один из путей понимания класса

N P состоит в том, чтобы рассматривать его как класс языков,

доказательства принадлежности к которым найти быть может

и трудно, но зато эти доказательства легко проверить.

Предположим, однако, что при выяснении принадлежности

x ∈ L для некоторого языка L ∈ N P мы не хотим смотреть все

доказательство.

Вместо этого мы хотим осуществить несколько случайных

проверок и затем с достаточной уверенностью констатировать,

что доказательство корректно.

Говоря неформально, система вероятностной проверки до-

казательств (Probabilistically Checkable Proof System, PCP, мы

будем назвать ее PCP-системой) для некоторого языка со-

стоит из полиномиальной проверяющей вероятностной маши-

ны Тьюринга (ВМТ), имеющей специальный доступ к отдель-

ным битам бинарной строки, представляющей доказательство.

Предоставлением этой строки занимается специальный оракул,

понятие, часто используемое в теории сложности и обознача-

ющее устройство, способное находить ответы на поставленные

ему вопросы. Машины Тьюринга (детерминированные, неде-

терминированные, вероятностные) сопрягаются с этим устрой-

ством путем установки в каждую машину отдельной ленты.

На этой ленте они пишут вопросы к оракулу и после перехода

в специальное состояние «обращение к оракулу» за один такт

работы получают на этой ленте ответ. Обычно ограничивают-

ся оракулами, возвращающими один бит, например, оракул мо-

жет заниматься распознаванием некоторого языка, возвращая