Кузюрин Н.Н. Фомин С.А. Эффективные алгоритмы и сложность вычислений

Подождите немного. Документ загружается.

6.3. Вероятностные вычисления 241

ний, полезную для описания классов сложностей задач, но,

увы, не соответствующую никаким реальным вычислительным

устройствам. Однако оказалось, что можно частично исполь-

зовать мощь «параллельного перебора», присущую НМТ, при-

внеся в детерминированный процесс вычисления вероятност-

ную составляющую. Выяснилось, что такие устройства вполне

можно построить физически, и что они способны эффективно

решать больший класс задач, чем обыкновенные МТ.

Впрочем, по-порядку. Сначала определим ВМТ — вероят-

ностную машину Тьюринга. Существует два подхода к опреде-

лению ВМТ, приведем их оба.

Определение 6.3.1. Вероятностная машина Тьюринга

аналогична недетерминированной машине Тьюринга, только

вместо недетерминированного перехода в два состояния ма-

шина выбирает один из вариантов с равной вероятностью.

Определение 6.3.2. Вероятностная машина Тьюринга

представляет собой детерминированную машину Тьюринга

(см. определение 6.1.1 «Машина Тьюринга»), имеющую допол-

нительно источник случайных битов, любое число которых,

например, она может «заказать» и «загрузить» на отдель-

ную ленту и потом использовать в вычислениях обычным для

МТ образом.

Оба определения — 6.3.1 «online ВМТ» и 6.3.2 «oﬀline

ВМТ» — очевидно, эквивалентны. Более того, они вполне со-

ответствуют обычному компьютеру, к которому подключен

внешний генератор случайных последовательностей на основе

случайных физических процессов, таких, как, например, рас-

пад долгоживущего радиоактивного изотопа (замер времени

между щелчками счетчика Гейгера рядом с образцом изотопа

рубидия-85), снятие параметров с нестабильных электрических

цепей и т. п.

242 Глава 6. Основы теории сложности вычислений

Привнесение случайности в детерминированную вычисли-

тельную модель (как и привнесение недетерминизма) модифи-

цирует понятие разрешимости. Теперь, говоря о результате ра-

боты ВМТ M на входе x, мы можем говорить о математическом

ожидании результата E[M(x)] или вероятности вывода того или

иного ответа на заданном входе: P[M(x) = 1], P[M(x) = 0], но

ограничение на время работы (как правило, полиномиальное)

понимается так же, как и для ДМТ.

Вообще, есть вероятностные алгоритмы, не совершающие

ошибок при вычислении. Они используют «вероятностную со-

ставляющую» для «усреднения» своего поведения на различ-

ных входных данных таким образом, чтобы избежать случая,

когда часто встречаются «плохие» входные наборы. Такие ал-

горитмы иногда называют «шервудскими», в честь известного

разбойника-перераспределителя ценностей, и мы уже рассмат-

ривали один из таких алгоритмов — алгоритм 12 «Quicksort»

с вероятностным выбором оси.

ВМТ может быть полезна, как мы увидим дальше, даже

если будет иногда ошибаться при вычислении некоторой функ-

ции. Разумеется, нас будут интересовать машины, ошибающи-

еся «нечасто» и, желательно, работающие эффективно, т. е. по-

линомиальное от длины входа время.

Мы сконцентрируемся на анализе ВМТ, применяющихся

для задач разрешения, т. е. задач, в которых нужно получить

ответ «0» или «1».

Рассматривая ВМТ, предназначенные для решения таких

задач, можно их классифицировать на три основные группы:

1) «zero-error» — ВМТ, не допускающие ошибок. Правда,

в этот же класс попадают алгоритмы, которые хоть и не

допускают ошибок, могут и не выдать никакого ответа

или отвечать «не знаю».

2) «one-sided error» — ВМТ с односторонними ошибками.

Например, ВМТ-«автосигнализация» обязательно срабо-

6.3. Вероятностные вычисления 243

тает, если стекло разбито, дверь открыта и происходит

автоугон, но могут произойти и ложные срабатывания

(так называемые ошибки второго рода, напомним также,

что ошибкой первого рода является «пропуск цели»).

3) «two-sided error» — ВМТ с двусторонними ошибками.

Ошибки могут быть и первого, и второго рода, но веро-

ятность правильного ответа должна быть больше (чем

больше, тем лучше)

, иначе эта ВМТ ничем не лучше

обычной монетки.

Далее мы более подробно рассмотрим перечисленные клас-

сы ВМТ и классы языков, эффективно (т. е. полиномиально)

распознаваемых ими.

6.3.1. Классы RP/coRP.



Односторонние ошибки



Итак, определим классы языков, эффективно распознаваемых

на ВМТ с односторонней ошибкой.

Определение 6.3.3. Класс сложности RP (Random Polyno-

mial-time) состоит из всех языков L, для которых существу-

ет полиномиальная ВМТ M, такая, что:

x ∈ L ⇒ P [M(x) = 1] ≥

x /∈ L ⇒ P [M(x) = 0] = 1.

Cразу же представим аналогичное определение для класса-

дополнения coRP ≡ {L|L ∈ RP}.

Определение 6.3.4. Класс сложности coRP (Complementary

Random Polynomial-time) состоит из всех языков L, для кото-

рых существует полиномиальная ВМТ M, такая, что:

244 Глава 6. Основы теории сложности вычислений

x ∈ L ⇒ P [M(x) = 1] = 1,

x /∈ L ⇒ P [M(x) = 0] ≥

Попробуем «популярно представить» языки и ВМТ, упо-

мянутые в этих определениях. Например, для определе-

ния 6.3.3 «RP» можно представить автоматическую систему

биометрической идентификации на входе в военный бункер,

никогда не пускающую солдат противника (x /∈ L), и с веро-

ятностью ≥

пускающей своих (x ∈ L), правда, возможно,

своим потребуется сделать несколько попыток прохода.

Для определения 6.3.4 «coRP» можно представить автома-

тическую автомобильную сигнализацию, гарантированно по-

дающую сигнал при попытке угона (x ∈ L), и с вероятностью

≥

не поднимающую ложную тревогу, если происходит что-то

другое.

Действительно, первое условие из определения 6.3.4 «coRP»

и второе условие из определения 6.3.3 «RP» называют

«completeness»-условиями

, а первое условие из определе-

ния 6.3.3 «RP» и второе условие из определения 6.3.4 «coRP» —

«soundness»-условиями

. Для тех, кто считает, что сигнализа-

ция с вероятностью ложного срабатывания чуть меньше

не

отличается здравостью и ни на что не годна, просим немного

подождать.

Вспомним, что в «oﬄine»-определении ВМТ (См. опреде-

ление 6.3.2 «oﬀline ВМТ») подразумевается отделенность ве-

роятностных данных от обычной ДМТ. Полиномиальная ВМТ

делает не более чем полиномиальное (от длины входа) число

переходов, и, следовательно, моделирующая ее ДМТ нужда-

ется не более чем в полиномиальной строке случайных битов.

Теперь перепишем еще раз определения классов RP и coRP,

completeness — полнота.

soundness — корректность.

6.3. Вероятностные вычисления 245

используя только ДМТ. Выделим элемент случайности в стро-

ку y, причем |y| ≤ p(|x|), где p(·) — некий полином, и заменим

условия на вероятность условиями на долю строк y, на которых

ДМТ дает тот или иной результат.

Определение 6.3.5. Класс сложности RP состоит из всех

языков L, для которых существуют некий полином p(·) и по-

линомиальная МТ M(x, y), такая, что:

x ∈ L ⇒

|{y : M(x, y) = 1, |y| ≤ p(|x|)}|

p(|x|)

≥

x /∈ L ⇒ ∀y M(x, y) = 0.

Определение 6.3.6. Класс сложности coRP состоит из

всех языков L, для которых существуют некий полином p(·)

и полиномиальная МТ M(x, y), такая, что:

x ∈ L ⇒ ∀y M(x, y) = 1,

x /∈ L ⇒

|{y : M(x, y) = 0, |y| ≤ p(|x|)}|

p(|x|)

≥

Теперь вспомним определение класса N P через детермини-

рованную машину Тьюринга (определение 6.2.4 «N P/ДМТ»)

и сравним его с определением 6.3.5 «RP/ДМТ», опуская оди-

наковые описания M, y:

N P RP

x ∈ L ⇒ ∃y, M(x, y) = 1 x ∈ L ⇒ доля y: M(x, y) = 1 ≥

x /∈ L ⇒ ∀y, M(x, y) = 0 x /∈ L ⇒ ∀y, M(x, y) = 0

246 Глава 6. Основы теории сложности вычислений

Стрелки показывают вложенность классов сложности

Ð²

coRP

Ð²

coNP

Ð²

Рис. 6.11. Классы сложности RP и coRP

Из этого сравнения видно, что класс RP вложен в класс

N P. Если для распознавания языка L из N P нам для каждого

x ∈ L нужен был хотя бы один полиномиальный «свидетель»

y, который мы могли предъявить «верификатору», то в случае

с классом RP этих свидетелей должно быть достаточно много,

согласно определению 6.3.5 «RP/ДМТ» не меньше половины.

На самом деле, как мы увидим дальше, этих свидетелей может

быть и меньше, а пока очевидны следующие утверждения (см.

рис. 6.11):

Теорема 6.3.1. RP ⊆ N P.

Теорема 6.3.2. coRP ⊆ coN P.

Теперь вернемся к пресловутой «одной второй». Рассмотрим

некоторый класс

Определение 6.3.7. Класс сложности

C состоит из всех

языков L, для которых существует полиномиальная ВМТ

такая, что:

x ∈ L ⇒ P [

M(x) = 1] ≥

x /∈ L ⇒ P [

M(x) = 1] = 0.

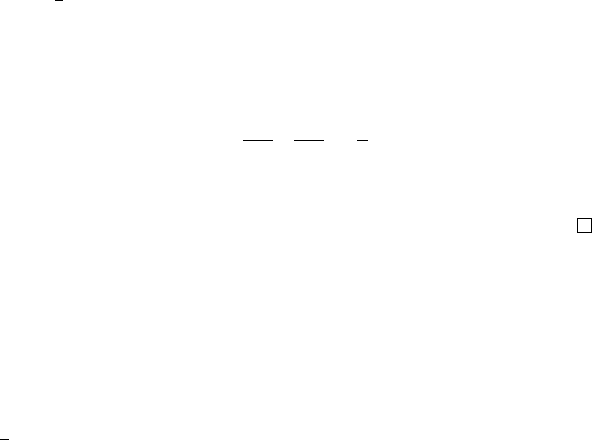
6.3. Вероятностные вычисления 247

Очевидно, т.к. с виду налагаемые условия кажутся более

(и уж точно не менее) жесткими,

C ⊆ RP. Можем ли мы утвер-

ждать, что RP ⊆

C и, следовательно,

C ≡ RP?

Оказывается, да.

Лемма 6.3.3. RP ⊆

C, и, следовательно,

C ≡ RP.

Доказательство. Допустим L ∈ RP. Тогда существует ВМТ

M(x) со свойствами, описанными в определении 6.3.3 «RP».

Для заданного x будем запускать машину M два раза, обозна-

чая результаты запусков через M

(x) и M

(x). Построим маши-

ну

M, дважды вызывающую машину M и выдающую в качестве

результата M

(x) ∨ M

(x). Тогда вероятность ошибки первого

рода (других ошибок машина M не допускает), случающейся,

когда x ∈ L, а M(x) = 0 (обозначим эту вероятность p

), будет

меньше

. Машина

M, по построению, тоже будет допускать

только ошибки первого рода, но они будут происходить только

в случае ошибки машины M на обоих запусках M

(x) и M

(x),

и вероятность такой ошибки будет

Соответственно, для заданного языка L построенная нами ма-

шина

M удовлетворяет описанию языка

Примененный нами метод называется «вероятностным уси-

лением» (или «вероятностной амплификацией» от ampliﬁcation),

и, применив его полиномиальное число раз, мы добиваемся

экспоненциального уменьшения вероятности ошибки. Таким

образом, уже очевидно, что в определениях RP и coRP вме-

сто «одной второй» можно использовать любые константы

≥

— с помощью амплификации мы легко можем достичь

заданного уровня «здравости».

Можно вполне использовать упоминающуюся шумную

сигнализацию, срабатывающую ложно в половине случаев,

248 Глава 6. Основы теории сложности вычислений

если заставить ВМТ сигнализации выполнить проверку раз

двадцать — тогда вероятность ложной тревоги была бы

меньше

10000

. Это, к сожалению, пока является недостижи-

мым уровнем для существующих автосигнализаций.

Более того, «порог», после которой можно «усиливать» ве-

роятность, не обязательно должен быть больше одной второй,

он может быть даже очень малым, главное, не быть пренебре-

жимо малым.

Определение 6.3.8. Класс сложности RP

weak

состоит из

всех языков L, для которых существуют полиномиальная

ВМТ M и полином p(·), такие, что:

x ∈ L ⇒ P [M(x) = 1] ≥

p(|x|)

x /∈ L ⇒ P [M(x) = 1] = 0.

Определение 6.3.9. Класс сложности RP

strong

состоит из

всех языков L, для которых существуют полиномиальная

ВМТ M и полином p(·), такие, что:

x ∈ L ⇒ P [M(x) = 1] ≥ 1 − 2

−p(|x|)

x /∈ L ⇒ P [M(x) = 1] = 0.

Поначалу кажется, что RP

weak

— это некоторая релакса-

ция, т. е. определение более широкого класса из-за ослабления

ограничений, класса RP, а RP

strong

, наоборот, усиление огра-

ничений, и, по крайней мере:

strong

⊆ RP ⊆ RP

weak

Однако оказывается, все это определения одного и того же

класса.

Лемма 6.3.4. RP

weak

= RP

strong

= RP.

6.3. Вероятностные вычисления 249

Доказательство. Достаточно доказать RP

weak

⊆ RP

strong

для чего мы покажем, как для любого языка L ∈ RP

weak

из ма-

шины M

weak

(машина M из определения 6.3.8) сделать машину

strong

, соответствующую определению 6.3.9. Действуем, как

и в более простом случае леммы 6.3.3 — для данного x машина

strong

запускает t раз машину M

weak

и возвращает Логическое

ИЛИ от всех результатов запуска. Так же, как и в случае лем-

мы 6.3.3, возможна только ошибка первого рода, причем ее

вероятность (если x ∈ L):

P(M

strong

(x) = 0) = (P(M

weak

(x) = 0))

t(|x|)



1 −

p(|x|)



t(|x|)

Осталось найти необходимое «для разгона» количество запус-

ков:



1 −

p(|x|)



t(|x|)

≤ 2

−p(|x|)

откуда получаем

t(|x|) ≥ −

log 2 p(|x|)

log



1 −

p(|x|)



≥ log 2 · p

(|x|).

т. е. за полиномиальное время мы усиливаем вероятность от

«полиномиально малой» до «полиномиально близкой к едини-

це».

6.3.2. Класс BPP.



Двусторонние ошибки



Теперь рассмотрим, что происходит, если допустить возмож-

ность двусторонних ошибок, т. е. ошибок первого и второго ро-

да. Определим класс языков, эффективно распознаваемых на

ВМТ с двусторонней ошибкой.

Определение 6.3.10. Класс сложности BPP (Bounded-

Probability Polynomial-time) состоит из всех языков L, для

250 Глава 6. Основы теории сложности вычислений

которых существует полиномиальная ВМТ M, такая, что:

x ∈ L ⇒ P [M(x) = 1] ≥

x /∈ L ⇒ P [M(x) = 0] ≥

Из определения видно, что класс BPP замкнут относитель-

но дополнения.

По опыту раздела 6.3.1 читатель ожидает обобщений опре-

деления класса BPP без магической константы «

», и мы его

не разочаруем. Итак, предоставим «свободное» и «жесткое»

определения класса BPP.

Определение 6.3.11. Класс сложности BPP

weak

состоит

из всех языков L, для которых существуют:

c, 0 < c < 1 — константа;

p(·) — положительный полином;

M — полиномиальная ВМТ;

такие, что:

x ∈ L ⇒ P [M(x) = 1] ≥ c +

p(|x|)

x /∈ L ⇒ P [M(x) = 1] < c −

p(|x|)

Определение 6.3.12. Класс сложности BPP

strong

состоит

из всех языков L, для которых существуют полиномиальная

ВМТ M, и полином p(·), такие, что:

x ∈ L ⇒ P [M(x) = 1] ≥ 1 − 2

−p(|x|)

x /∈ L ⇒ P [M(x) = 0] ≥ 1 − 2

−p(|x|)

В следующей лемме мы используем следующие результаты

из теории вероятностей.