Кузюрин Н.Н. Фомин С.А. Эффективные алгоритмы и сложность вычислений

Подождите немного. Документ загружается.

3.4. Точность алгоритма для почти всех входов 131

двух направлениях: во-первых, мы рассматриваем не только

точные алгоритмы, но и приближенные, а во-вторых, анализ

сложности в среднем заменяется на анализ для «почти всех»

исходных данных.

Ранее мы доказали, что для задачи о покрытии жадный

алгоритм (см. раздел 2.1.1) в худшем случае гарантирует на-

хождение покрытия, размер которого превосходит размер ми-

нимального покрытия не более чем в логарифмическое число

раз (по m). Наша цель сейчас — показать, что для «типичных»

данных (в отличие от худшего случая, см. упражнение 2.1.2)

это отношение близко к единице, т. е. размер покрытия, найден-

ного жадным алгоритмом, почти равен размеру минимального

покрытия.

Как и в предыдущем разделе, мы будем использовать фор-

мулировку задачи о покрытии на языке (0, 1)-матриц и цело-

численных линейных программ:

cx → min,

Ax ≥ b,

∀j x

∈ {0, 1}.

(3.5)

В этой целочисленной линейной программе n столбцов-пе-

ременных x

, . . . , x

соответствуют подмножествам S

, . . . , S

и их включению в решение-покрытие. Матрица A также явля-

ется матрицей инцидентности, а векторы стоимости и ограни-

чений — также векторы размерности n и m соответственно,

состоящие полностью из единиц.

Таким образом, m строк-ограничений, соответствующих m

предметам, очевидным образом выражают ограничение на обя-

зательное включение предмета хотя бы в одно из покрывающих

подмножеств, а целевая функция равна числу таких подмно-

жеств.

Как и в разделе 3.2, предположим, что A = (a

) — случай-

132 Глава 3. Вероятностный анализ алгоритмов

ная (0,1)-матрица, такая, что для всех i, j выполнено

P {a

= 1} = p, P{a

= 0} = 1 − p.

Пусть R

, где Z

— величина покрытия, найденного

жадным алгоритмом, а M — величина минимального покры-

тия. Наш основной результат заключается в следующей теоре-

ме.

Теорема 3.4.1. Пусть вероятность 0 < p < 1 фиксирована,

и пусть для задачи (3.5) со случайной матрицей A, опреде-

ленной выше, выполнены следующие условия:

∀γ > 0

ln n

→ 0, при n → ∞, (3.6)

ln m

→ 0, при n → ∞. (3.7)

Тогда для любого фиксированного ε > 0

P{R

≤ 1 + ε} → 1 при n → ∞.

Заметим, что условия теоремы требуют, чтобы матрица

A не была «экспоненциально вытянутой» по высоте или ши-

рине. В частности, для «пропорциональных» матриц, у кото-

рых m = cn, где c — некоторая константа, и «несильно переко-

шенных матриц», у которых m = O(n

), условия (3.6) и (3.7)

теоремы 3.4.1 выполнены автоматически.

Доказательство. Сначала докажем нижнюю оценку размера

минимального покрытия.

Пусть X — случайная величина, равная числу покрытий

размера

= l

(δ) = −d(1 − δ) ln m/ ln(1 − p)e,

тогда

E X =





P (l

3.4. Точность алгоритма для почти всех входов 133

где P(l

) — вероятность того, что фиксированные l

столбцов

являются покрытием A. Нетрудно увидеть (убедитесь, что это

действительно нетрудно!), что

P(l

) =



1 − (1 − p)



≤ exp{−m(1 − p)

Используя неравенство





≤ n

, получаем

ln E X ≤ l

ln n − m(1 − p)

≤

≤ −

ln m

ln(1 − p)

ln n − m exp



−(1 − δ) ln(1 − p)

ln m

ln(1 − p)



≤

≤ −

ln m

ln(1 − p)

ln n − mm

−1

≤ −

ln m

ln(1 − p)

ln n − m

Проверим, что для любого фиксированного 0 < δ < 1 при

условиях (3.6) последнее выражение стремится к −∞ при

n, стремящемся к бесконечности. Действительно, положив

γ = δ/2 в условии 3.6, получим требуемое, т.к. ln m растет

медленнее, чем m

δ/2

Таким образом, вероятность того, что нет покрытия раз-

мера l

в случайной (0, 1)-матрице, стремится к 1, поскольку

согласно первому неравенству Чебышева

P{X ≥ 1} ≤ E X → 0.

Последнее означает, что P{M ≥ l

} → 1.

Теперь докажем верхнюю оценку размера покрытия, по-

строенного жадным алгоритмом.

Используем следующую известную лемму [AS92] о вероят-

ности больших уклонений для сумм независимых случайных

величин.

Иногда упоминается как неравенство Маркова.

134 Глава 3. Вероятностный анализ алгоритмов

Лемма 3.4.2. Пусть Y — сумма n независимых случайных

величин, каждая из которых принимает значение 1 с вероят-

ностью p и 0 с вероятностью 1 − p. Тогда

P{|Y − np| > δnp} ≤ 2 exp{−(δ

/3)np}.

По этой лемме вероятность того, что некоторая фиксиро-

ванная строка содержит менее чем (1 − δ)pn единиц (или более

чем (1 + δ)pn единиц) оценивается сверху так:

bad

≤ 2 exp{−(δ

/3)np},

и математическое ожидание числа таких строк не превос-

ходит mP

bad

. Тогда при n → ∞, по условию (3.7) получаем

bad

≤ 2 exp{ln m − (δ

/3)np} = 2 exp{ln m − O(1)n} → 0.

Из P{X ≥ 1} ≤ E X — первого неравенства Чебышева сле-

дует, что вероятность события «каждая строка содержит не

менее (1 − δ)pn единиц» стремится к 1.

Теперь мы можем почти дословно повторить получение

верхней оценки размера покрытия, построенного жадным ал-

горитмом, в худшем случае.

Пусть N

— число непокрытых строк после t-го шага жад-

ного алгоритма. Подсчитывая нижнюю оценку числа единиц

в подматрице, образованной непокрытыми строками (N

t−1

), и

делая вывод о существовании столбца в этой подматрице с чис-

лом единиц не менее среднего, имеем:

≤ N

t−1

−

t−1

(1 − δ)pn

= N

t−1

(1 − (1 − δ)p) ≤

≤ N

(1 − (1 − δ)p)

= m(1 − (1 − δ)p)

Первое неравенство получается оценкой снизу суммарного

числа единиц в подматрице из N

t−1

непокрытых строк (это

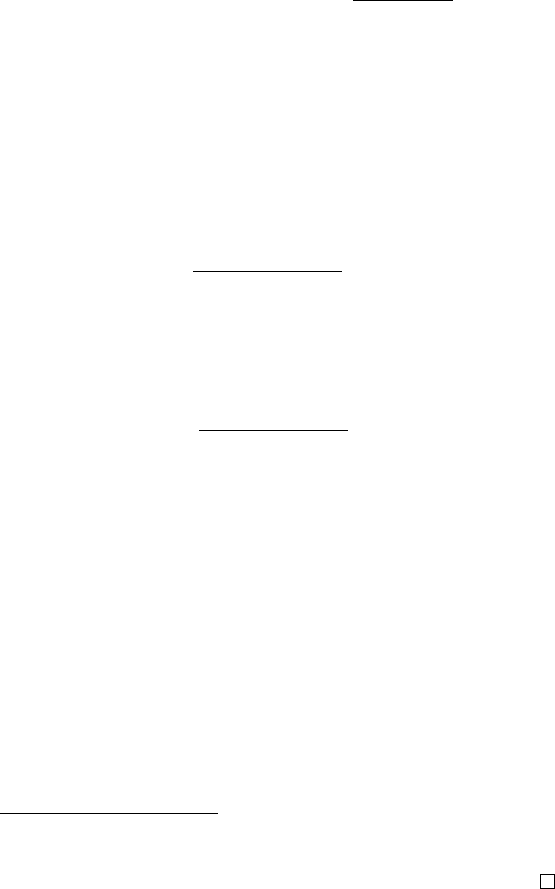
3.4. Точность алгоритма для почти всех входов 135

t−1

(1 − δ)pn) и выводом, что найдется столбец, содержащий

не менее среднего числа единиц (равного

t−1

(1−δ)pn

)

Найдем максимальное t, при котором еще есть непокрытый

элемент:

m(1 − (1 − δ)p)

≥ 1.

Получим

ln m + t ln(1 − (1 − δ)p) ≥ 0,

или

t ≤ −

ln m

ln(1 − (1 − δ)p)

Отсюда получается верхняя оценка мощности «жадного по-

крытия» (Z

= t + 1) в типичном случае:

P(Z

≤ 1 −

ln m

ln(1 − p(1 − δ))

) → 1.

Комбинируя это неравенство с нижней оценкой, можно по-

лучить, что для любого фиксированного ε > 0 и достаточно

больших n

P(R

≤ 1 + ε) → 1.

Действительно,

ln(1 − p(1 − δ)) ≥ ln(1 − p),

и для любого ε > 0 существует δ > 0, такое, что

≤

ln(1 − p)

(1 − δ) ln(1 − p(1 − δ))

+ o(1) ≤ (1 − δ)

−1

+ o(1) ≤ 1 + ε.

136 Глава 3. Вероятностный анализ алгоритмов

3.5.



Рюкзак



: полиномиальность в сред-

нем

Полиномиальность «в среднем» алго-

ритма динамического программирова-

ния Немхаузера–Ульмана для задачи

о рюкзаке ([BV03]).

Итак, рассмотрим еще раз задачу 13 «Knapsack». Как мы

видели в разделе 2.2.1, для задачи 13 «Knapsack» существу-

ет алгоритм 25 «Рюкзак Немхаузера–Ульмана», поддерживаю-

щий в процессе своей работы множество парето-оптимальных

или, как иногда говорят, доминирующих решений (определе-

ние 2.2.1 «Парето-рюкзак»). Сложность этого алгоритма —

O(n·|ParetoSolutions|), т. е. напрямую зависит от конечного раз-

мера множества доминирующих решений для данного входного

рюкзака. И хотя можно показать, что существуют такие вход-

ные наборы, для которых размер множества доминирующих

решений будет экспоненциальным по n (упражнение 2.2.5), для

практических целей интересно проанализировать, насколько

«часто» встречаются такие плохие входные наборы, возмож-

но ли ожидать от этого алгоритма полиномиального времени

работы «в среднем».

Оказалось, справедлива следующая теорема, доказатель-

ство которой и составляет все содержание этого раздела.

Теорема 3.5.1. Пусть

— «веса», произвольные положительные числа;

— «стоимости», независимые случайные величины, равно-

мерно распределенные на [0, 1];

q = max |P aretoSolutions| — число доминирующих подмно-

жеств для всех n предметов.

3.5.



Рюкзак



: полиномиальность в среднем 137

Тогда

E(q) = O(n

Сначала введем некоторые определения.

Пусть m = 2

, S

, . . . , S

— подмножества [n] в поряд-

ке неубывания весов. Сразу заметим, что веса

i∈S

мно-

жеств S

в нашем рассмотрении не возникают.

Для фиксированной u ∈ [2 . . . m] и переменной k ∈ [1 . . . u)

определим:

P lus

— предметы в S

, которых нет в S

;

Minus

— предметы в S

, которых нет в S

;

— сумма стоимостей предметов в Plus

;

−

— сумма стоимостей предметов в Minus

;

— минимальная разность Δ

− Δ

−

, по всем k меньшим

u; условно говоря, это «максимальное преимущество

в стоимости» над всеми предыдущими подмножествами

, . . . , S

u−1

Или, более формально:

P lus

= S

\ S

Minus

= S

\ S

i∈P lus

−

i∈Minus

= min

1≤k<u

− Δ

−

138 Глава 3. Вероятностный анализ алгоритмов

Следующее утверждение следует напрямую из этих опре-

делений и определения 2.2.1 «Парето-рюкзак»:

Лемма 3.5.2. ∀u ≥ 2, S

— доминирующее множество тогда

и только тогда, когда Δ

> 0.

Учитывая, что стоимость самого последнего множества S

ограничена по крайней мере n, то интуитивно уже можно

утверждать, что чем больше в среднем будет прирост стоимо-

сти Δ

> 0 для каждого доминирующего набора u, тем мень-

ше в среднем будет размер всего множества парето-решений

P aretoSolutions.

Далее мы последовательно:

1) оценим вероятность «неблагоприятных» с точки зрения

минимизации размера P aretoSolutions событий, таких,

как небольшой прирост Δ

> 0 для нового доминиру-

ющего подмножества;

2) определим математическое ожидание прироста стоимо-

сти Δ

> 0 для нового доминирующего подмножества u;

3) получим мат. ожидание размера P aretoSolutions и, сле-

довательно, математическое ожидание времени работы

алгоритма.

Итак, рассмотрим некоторое u, пусть S

= [1, . . . , t] (это

только вопрос удобства — нам ничего не мешает перенумеро-

вать предметы в исходном наборе).

Тогда:

∀ 1 ≤ k < u P lus

⊆ [1, . . . , t], M inus

⊆ [t + 1, . . . , n].

Для некоторого параметра 0 < ε < 1 определим следующие

3.5.



Рюкзак



: полиномиальность в среднем 139

события с достаточно «говорящими» названиями:

ПаретоНабор = {Δ

> 0}

ДельтаМала =



< ε



ЭлементМал

= {c

< ε}

ЭлементНеМал

= ЭлементМал

= {c

≥ ε}

ВНабореНеМалы = ∩

j=1

ЭлементНеМал

Оценим вероятность того, что в доминирующем подмноже-

стве есть элемент с «малой» стоимостью.

Лемма 3.5.3. P(ВНабореНеМалы|ПаретоНабор) ≤ nε.

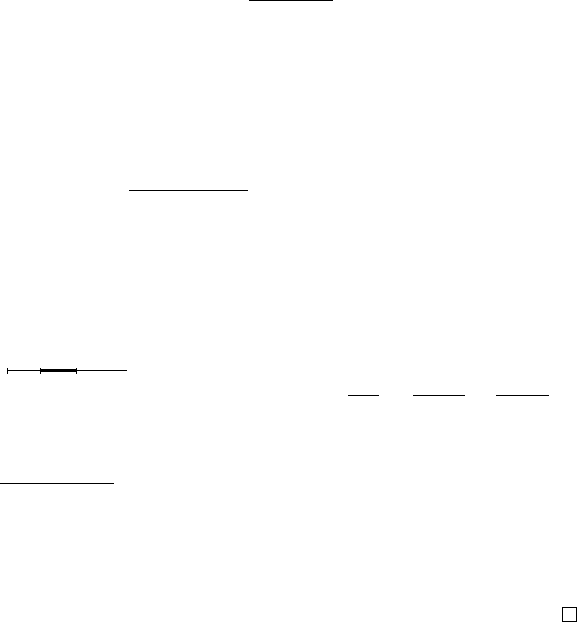
Доказательство. ∀j ≤ t и 0 < ε < 1 имеем для некоторого x:

P (c

< ε| ∀k : Δ

> Δ

−



= P (c

< ε| c

> x) ≤

0 x ε 1

P(c

< ε|c

> x)

≤

(

при x ≥ ε: 0

при x < ε:

ε−x

1−x

ε(1−x)

1−x

−

x(1−ε)

1−x

≤ ε.

P(ВНабореНеМалы|ПаретоНабор) = P(∪

j=1

ЭлементМал

|ПаретоНабор) ≤

≤

j=1

P(ЭлементМал

|ПаретоНабор) ≤ t · ε ≤ nε.

Теперь оценим вероятность того, что прирост стоимости

доминирующего подмножества будет «мал», при условии, что

в наборе нет «малых» предметов.

Лемма 3.5.4. P(ДельтаМала|ПаретоНабор ∧ ВНабореНеМалы) ≤ nε.

140 Глава 3. Вероятностный анализ алгоритмов

Доказательство. Оценим P(ПаретоНабор) при априорности собы-

тий (при условии): «∀j c

∈ [0, 1]», «ВНабореНеМалы»(и, следова-

тельно, «Δ

≥ ε»):

P(ПаретоНабор|ВНабореНеМалы) =

= P



∀k Δ

−

≤ Δ

, ∀j > t c

∈ [0, 1]



(1 − ε)

n−t



∀k Δ

−

≤ (1 − ε) Δ

, ∀j > t c

∈ [0, 1 − ε]



≤

(1 − ε)

n−t



∀k Δ

−

≤ Δ

− ε

, ∀j > t c

∈ [0, 1 − ε]



≤

(1 − ε)

n−t

P (ДельтаМала|ВНабореНеМалы) .

Здесь был использован известный факт из геометрии: объем

политопа (выпуклой области, задаваемой системой неравенств

в (n − t)-мерном пространстве), «уменьшенного» в 1 − ε раз,

меньше исходного в (1 − ε)

n−t

. А вероятность как раз и выра-

жалась через объем политопа!

С другой стороны, ДельтаМала ⊂ ПаретоНабор, и

P(ДельтаМала|ПаретоНабор ∧ ВНабореНеМалы) =

P(ДельтаМала|ВНабореНеМалы)

P(ПаретоНабор|ВНабореНеМалы)

≥ (1 − ε)

n−t

≥ (1 − ε)

≥ 1 − nε.

Далее нам понадобится небольшая техническая лемма из

теории вероятностей.

Лемма 3.5.5.

P(A|B) = P(A|B ∩ C) · P(C|B) + P(A|B ∩ C) · P(C|B).

Доказательство. Рассмотрим пересечение событий A, B, C,

где «разрезанные» части обозначены x, y, z, w: