Кузюрин Н.Н. Фомин С.А. Эффективные алгоритмы и сложность вычислений
Подождите немного. Документ загружается.

3.2. Задача упаковки 121
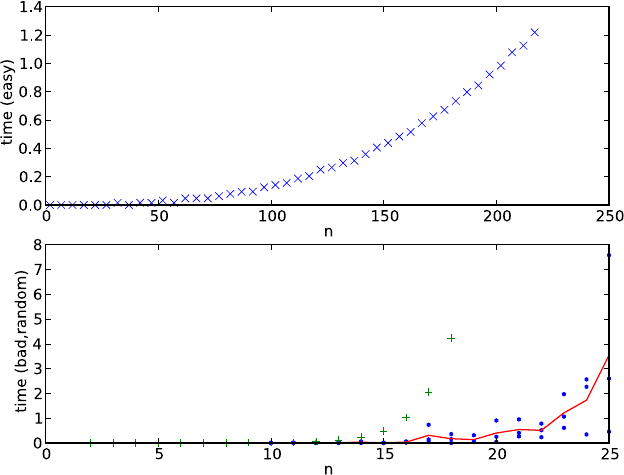
Некоторые экспериментальные результаты поведения алго-
ритма 28 «Упаковка-ДинПрог» на случайных данных, можно
увидеть на рисунке 3.2.
Время работы алгоритма 28 «Упаковка-ДинПрог» на квадратных матрицах
инцидентности в зависимости от n — числа множеств и элементов. Типы
матриц:
easy: Легкие для алгоритма наборы (см. упражнение 3.2.2).
bad: Тяжелые для алгоритма наборы, представлены крестиками.
random: Случайные матрицы инцидентности, сплошная линия — среднее вре-
мя работы.
Рис. 3.2. Алгоритм 28 «Упаковка-ДинПрог» на случайных данных
В заключение отметим, что из полученных результатов вы-
текает не только полиномиальный в среднем алгоритм для за-

122 Глава 3. Вероятностный анализ алгоритмов
дачи 15 «Packing», но и полиномиальный в среднем алгоритм
для более трудной задачи подсчета числа целых точек в мно-
гограннике, заданном ограничениями (3.1).
Рис. 3.3. Карта-памятка раздела 3.2.0
3.3. Выполнимость КНФ
Раздел основан на работе [Iwa89].
Задача 16. «Выполнимость/SAT»
2
. Дано булевское выраже-
ние, являющееся конъюнктивной нормальной формой
(КНФ):
CNF =
m
^
i=1
C
i
, (3.3)
где C
i
— элементарные дизъюнкции вида
x
σ
1
j
1
∨ . . . ∨ x
σ
k
j
k
, (3.4)
1 ≤ k ≤ n, σ
j
∈ {0, 1}, x
1
= x и x
0
= (¬x).
2
В англоязычной литературе — Satisfiability или просто SAT.
3.3. Выполнимость КНФ 123
Существует ли (булевский) набор переменных x
j
, обраща-
ющий эту форму в 1 (т. е. в «Истину»)?
Задаче 16 «SAT» выпала честь быть первой задачей, для ко-
торой была установлена N P-полнота (cм. раздел 6.2). И хотя
N P-полнота задачи, по сути, определяет «переборность» лю-
бого алгоритма для ее решения
3
, одни виды перебора могут
быть перспективнее других.
Итак, как можно организовать решение этой задачи?
Самым простым решением будет перебор всех входных на-
боров x = {x
1
, . . . , x
n
}, пока CNF (x) не станет равна единице.
Однако в худшем случае, например, если CNF невыполнима,
надо перебрать 2
n
наборов x.
Для некоторых формул этот перебор можно сократить, ес-
ли обеспечить подсчет размера множества невыполнимых на-
боров — |X
0
|, где X
0
= {x : CNF (x) = 0}. CNF невыполнима
тогда и только тогда, когда |X
0
| = 2
n
.
Остается вопрос: как подсчитать |X
0
| более эффективно,
нежели перебором x?
Введем (или напомним) несколько обозначений.
Определение 3.3.1. Литерал — каждое вхождение пе-
ременной x
i
(или ее отрицания) в скобку. Например, для
(x
1
∨ x
2
) ∧ (x
1
∨ x
3
) литералами будут x
1
, x
2
, x
1
, x
3
.
Для некоторого подмножества из k скобок S = {C
j
1
, . . . , C
j
k
}
мы обозначим через Lit
S
все литералы S, т. е. все литералы
lit ∈ {x
i
, x
i
}, входящие в S.
Рассмотрим некоторую КНФ (обозначим ее CN F (x)). На
каких наборах она равна нулю? Очевидно, если CNF (x) = 0,
то одна или несколько скобок-дизъюнкций C
j
(x) = 0.
Возьмем некоторое подмножество S = {C
j
1
, . . . , C
j
k
} из k
скобок и зададимся вопросом: когда все скобки в S будут рав-
ны нулю? Обозначим это утверждение предикатом Z
S
(x) = 1
3
Разумеется, при гипотезе P 6= NP

124 Глава 3. Вероятностный анализ алгоритмов
и раскроем определение:
Z
S
(x) =
k
^
i=1
C
j
i
=
k
^
i=1
_
lit∈C
j
i
lit =
^
lit∈Lit
S
lit.
т. е. Z
S
зависит только от множества литералов Lit
S
и не
зависит от распределения литералов по отдельным скобкам.
А для множества S возможны два варианта. Множество S мо-
жет быть:
зависимое — ∃i: литералы x
i
∈ Lit
S
и x
i
∈ Lit
S
. В этом слу-
чае Z
S
≡ 0, т. е. |x : Z
S
(x) = 1| = 0 — нет выполняющих
Z
S
наборов.
независимое — @i: x
i
∈ Lit
S
и x
i
∈ Lit
S
. Тогда есть вы-
полняющие Z
S
наборы x, причем каждая переменная
из Lit
S
может входить либо в положительной степени
и иметь значение «0», либо в отрицательной степени
и иметь значение «1». т. е. если x
3
∈ Lit
S
, то x
3
= 1, а ес-
ли x
7
∈ Lit
S
, то x
7
= 0. Для остальных переменных, не
входящих в Lit
S
, значение может быть любым. Поэтому
|x : Z
S
(x) = 1| = 2
n−|Lit
S
|
.
Итак, если ∃x : CN F (x) = 0, то существует некоторое неза-
висимое S. Для подсчета размера множества обнуляющих на-
боров |X
0
| построим все независимые множества и просумми-
руем для каждого независимого множества S число «обнуля-
ющих» наборов 2
n−|Lit
S
|
.

3.3. Выполнимость КНФ 125
x : Z
{C
1
}
= 1
x : Z
{C
2
}
= 1
x : Z
{C
3
}
= 1
C
1
, C
2
C
1
, C
2
, C
3
C
2
, C
3
C
1
, C
3
Рис. 3.4. «Обнуляющие» наборы для трехскобочной КНФ
Разумеется, напрямую суммировать нельзя, т.к. «обнуля-
ющие» наборы различных множеств пересекаются. Например,
рассмотрим трехскобочную (скобки C
1
, C
2
, C
3
) КНФ, у кото-
рой все наборы скобок {C
1
}, {C
2
}, {C
3
}, {C
1
, C
2
}, {C
1
, C
3
},
{C
2
, C
3
}, {C
1
, C
2
, C
3
} являются независимыми. Тогда множе-
ство «обнуляющих» наборов {x : Z
{C
1
}
= 1} включает в себя
множество {x : Z
{C
1
,C
2
}
= 1}, которое включает в себя, в свою
очередь, множество {x : Z
{C
1
,C
2
,C
3
}
= 1}.
Как раз для подсчета мощности объединения пересека-
ющихся множеств и применяется комбинаторная формула
включений-исключений
4
, утверждающая, что для конечных
множеств A
1
, . . . , A
n
мощность их объединения можно под-
считать по формуле
4
Вариант: «формула включения-исключения», в англоязычной литера-
туре — «inclusion-exclusion principle» или «sieve principle».

126 Глава 3. Вероятностный анализ алгоритмов
n
[
i=1
A
i
=
n
X
i=1
|A
i
| −
X
i,j : i<j
|A
i
∩ A
j
| +
+
X
i,j,k : i<j<k
|A
i
∩ A
j
∩ A
k
| − · · · · · · (−1)
n−1
|A
1
∩ · · · ∩ A
n
| .
В нашем случае A
i
обозначает множество наборов, для ко-
торых i-я скобка C
i
равна нулю, поэтому
|X
0
| = | ∪
m
i=1
A
i
|.
Далее удобно разбить все независимые множества на
«k-слои» N
k
: независимые множества с k скобками, и органи-
зовать суммирование включений-исключений по этим слоям:
|X
0
| =
m
X
k=1
(−1)
k−1
·
X
S∈N
k
2
n−|Lit
S
|
.
Осталось понять, как построить все независимые множе-
ства скобок. Оказалось, их также удобно строить «послойно»,
получая N
k+1
из N
k
попыткой «добавить» каждую скобку C
j
к каждому множеству из N
k
следующим образом:
for all C
j
∈ {C
1
, . . . , C
m
} do
for all S ∈ N
k
do
Lit
S
0
← Lit
S
for all lit ∈ C
j
do
if lit /∈ Lit
S
0
then
Lit
S
0
← Lit
S
0
∪ lit
else
отбрасываем зависимое C
j
+ S.
end if
end for
end for
end for

3.3. Выполнимость КНФ 127
В множество N
1
мы записываем все одиночные скобки,
являющиеся независимыми множествами. Заметим, что непо-
средственно для подсчета |X
0
| нет необходимости хранить все
независимые множества, достаточно хранить текущее N
k
(и
вычисляемое N
k+1
), и суммировать оценку |X
0
| по формуле
включений-исключений одновременно с построением N
k+1
.
Таким образом, мы получаем алгоритм 29.
Лемма 3.3.1. Сложность алгоритма 29 в наихудшем случае:
O(m
2
n · max
k
|N
k
|).
Доказательство. Действительно:
• цикл по «слоям» — O(m);
• цикл по скобкам — O(m);
• цикл по независимым множествам из k скобок — O(N
k
).
• цикл по литералам в скобке (проверка независимости
множества S = C
j
+ t) внесет множитель O(n);
Общая трудоемкость — O(m
2
n · max
k
|N
k
|).
Видно, что, как и в случае с другими алгоритмами дина-
мического программирования, время работы алгоритма опре-
деляется размером множества частичных решений (в данном
случае N
k
). В частности, оно может быть экспоненциальным.
Упражнение 3.3.1. Какие входные данные для алгоритма 29
заставят его работать экспоненциально долго?
С другой стороны, на многих входах этот алгоритм работа-
ет эффективно.
Упражнение 3.3.2. На каких входных данных этот алгоритм
будет работать O(m)?

128 Глава 3. Вероятностный анализ алгоритмов
Алгоритм 29. Динамическое программирование для «SAT»
def SatDynP (CNF) :
size ← 0 # счетчик выполняющих КНФ наборов
n ← CNF.numberOfVariables () # число переменных в КНФ
T ← {CNF.getEmptySetOfBraces () : CNF.getEmptySetOfLiterals ()}
for (k, dummy) ∈ enumerate (CNF): # цикл по слоям
S ← {} # новый слой независимых множеств
for j, C ∈ enumerate (CNF): # цикл по скобкам
for t ∈ T : # цикл по независимым множествам
if j 6∈ t: # если скобки в множестве нет
s ← t + j # добавляем её к множеству
if s 6∈ S : # в слое S нет такого множества?
lits ← copy (T [t]) # наследуем литералы из t
for x ∈ C : # для каждого литерала в C
ok ← −x 6∈ lits # x совместен с другими?
if ¬ok : break
lits.add (x)
if ok : # and len(lit)>len(T[t]):
S[s] ← lits # да, s —независимое
size ← size + 2 ** (n − len (lits)) ∗ (−1) ** k
T ← S
return size
CNF = (x
2
∨ x
3
∨ x
1
) ∧ (x
3
∨ x
2
) ∧ (x
1
∨ x
3
) ∧ (x
1
∨ x
2
∨ x
4
)
k size T
0 0 {}: {}
1 12 {C
0
}: {x
2
, x
3
, x
1
}, {C
3
}: {x
1
, x
2
, x
4
}, {C
1
}: {x
3
, x
2
}, {C
2
}: {x
1
, x
3
}
2 11 {C
2
, C
3
}: {x
1
, x
2
, x
4
, x
3
}
3 11
end 11
11 < 2
4
→ КНФ выполнима.
CNF = (x
3
∨ x
2
) ∧ (x
1
∨ x
3
) ∧ (x
3
∨ x
1
) ∧ (x
2
∨ x
3
)
k size T
0 0 {}: {}
1 8 {C
0
}: {x
3
, x
2
}, {C
3
}: {x
2
, x
3
}, {C
1
}: {x
1
, x
3
}, {C
2
}: {x
3
, x
1
}
2 8
3 8
end 8
8 = 2
3
→ КНФ невыполнима.
3.3. Выполнимость КНФ 129
Для оценки практичности алгоритма попробуем ввести
некоторое вероятностное распределение входных данных и
оценить сложность алгоритма в среднем.
Теорема 3.3.2. Пусть для каждой скобки вероятность появ-
ления каждой из n переменных (или ее отрицания) равна p,
причем
np
2
≥ ln m.
Тогда алгоритм 29 является полиномиальным в среднем.
Доказательство. Для доказательства достаточно будет оце-
нить сверху математическое ожидание |N
k
|.
Пусть S
k
— некоторое множество скобок, |S
k
| = k.
Вероятность того, что внутри одной скобки x
i
«не встре-
тится» с ¬x
i
равна 1 − p
2
. Вероятность ˜p
i
(S
k
), что x
i
избежит
встречи с ¬x
i
в каждой из k скобок S
k
равна
˜p
i
(S
k
) = (1 − p
2
)
k
.
Обозначим через p
i
(S
k
) вероятность, что в S
k
нет одновре-
менно x
i
и ¬x
i
.
Эта вероятность p
i
(S
k
), очевидно не больше вероятности
˜p
i
(S
k
), ибо в последнем случае разрешается x
i
встретиться с
¬x
i
, если они будут в разных скобках (поскольку мы оцениваем
дополнения событий, то дополнение к более узкому событию и
дает верхнюю оценку), поэтому
p
i
(S
k
) ≤ (1 − p
2
)
k
.
Теперь оценим вероятность того, что S
k
— независимое мно-
жество, обозначив ее через P (S
k
):
P (S
k
) =
n
Y
i=1
p
i
(S
k
) ≤ (1 − p
2
)
kn
.
Видно, что эта вероятность зависит только от размера мно-
жества S
k
, поэтому дальше будем обозначать ее через P (k).
130 Глава 3. Вероятностный анализ алгоритмов
Теперь можно оценить математическое ожидание max
k
|N
k
|:
E max
k
|N
k
| ≤
m
X
k=1
m
k
P (k) ≤
m
X
k=1
m
k
(1 − p
2
)
kn
≤
≤
m
X
k=1
m
k
exp{−np
2
k} ≤
m
X
k=1
exp{k(ln m − np
2
)} ≤
m
X
k=1
1 = m.
Упражнение 3.3.3. Докажите, что
E max
k
|N
k
| ≤
m
X
k=1
m
k
P (k).
Рис. 3.5. Карта-памятка раздела 3.3.0
3.4. Точность алгоритма для почти всех
входов
Хотя человека, использующего жадный алгоритм, можно за-
ставить сильно ошибиться при принятии сложных реше-
ний (например, при решении N P-трудных задач), в типич-
ном случае он обычно выигрывает. Этот почти философский
тезис будет нами проиллюстрирован на примере жадного ал-
горитма для задачи о покрытии.
В данном разделе мы рассмотрим некоторое ослабление
анализа сложности в среднем. Это ослабление происходит в
