Кузнецов В.П., Лукьянец С.В., Крупская М.А. Теория автоматического управления. Часть 1: Линейные непрерывные системы
Подождите немного. Документ загружается.


121
∑
∑
+
+
+
y
∑
∑
+
+
+
y
e
∑
+
f
υ
−
−
−
υ
()
f
K
Ws
()
K
Ws
υ
Рис. 9.5
Для структуры, изображенной на рис. 9.5, а, имеем
312
123
()[()()()]
()()
1()()()
K
WsWsWsWs
YsVs
WsWsWs
υ
+
=
+
, (9.10)
а для структуры на рис. 9.5, б имеем
32
123
()[1()()]
()()
1()()()
f
K
WsWsWs
YsFs
WsWsWs
−
=
+
. (9.11)
Задача любой системы автоматического управления – как можно более
точно воспроизвести управляющий (полезный) сигнал
()
t
υ
и максимально
ослабить влияние возмущения на выходной сигнал. С этой точки зрения
желательно, чтобы в (9.10) передаточная функция, связывающая
)
(
s
Y
и
)
(
s
V
,
была равна единице (тогда
()()
tyt
υ
=
), а передаточная функция в (9.11),
связывающая
)
(
s
Y
и
)
(
s
F
, была равна нулю (тогда
)
(
t
f
не влияет на
)
(
t
y
).
Выполнением этих условий будут соответственно следующие
соотношения:

122
3
1
()
()
K
Ws
Ws
υ
= , (9.12)
)(
1
)(
2
sW
sW
f
K
= . (9.13)
Условия (9.12), (9.13) соответствуют так называемой полной
инвариантности системы. При выполнении (9.12) передаточная функция,
связывающая ошибку е и входной сигнал
υ
, как это нетрудно проверить, будет
равна нулю, т.е. ошибка в системе не зависит (инвариантна) от управляющего
сигнала и всегда равна нулю. При выполнении (9.13) выход системы y не
зависит (инвариантен) от возмущения f.
Отметим, что условия (9.12), (9.13) гарантируют инвариантность
соответствующих координат с точностью до свободной составляющей, т.е.
процессы, вызванные начальными отклонениями соответствующих координат и
их производных, компенсироваться не будут.
Сравнивая (9.9)–(9.11), приходим к выводу, что характеристическое
уравнение нескорректированной системы (9.9) и скорректированных систем
(9.10), (9.11) одно и то же:
0)()()(1)(
321
=
λ
λ
λ
+
=
λ
WWWD , (9.14)
т.е. коррекция по внешнему воздействию не изменяет характеристического
уравнения системы и соответственно свойств устойчивости (запасов
устойчивости), а также ряда других показателей качества переходных
процессов.
В силу этого контур управления по отклонению, как правило, используют
для придания определенных динамических свойств системе, а контуры
коррекции по внешним воздействиям – для обеспечения точности.
Точное выполнение условий инвариантности (9.12), (9.13) практически
невозможно из условий физической реализуемости. Действительно, если в
(9.12), (9.13) передаточные функции )(
2
sW , )(
3
sW соответствуют физически
реализуемым звеньям, т.е. степени полиномов относительно
s
их числителя
меньше степеней знаменателя, то передаточные функции
()
K
Ws
υ
и )(sW
f
K
,
обратные им, будут соответствовать физически нереализуемым звеньям.
Поэтому (9.12), (9.13) выполняются на практике с некоторой
погрешностью, в силу чего и инвариантность систем будет неполной, но
ошибки в системе с помощью корректирующих устройств по внешнему
воздействию могут быть значительно уменьшены.
9.4. Синтез САУ на основе логарифмических частотных
характеристик
Общий порядок синтеза системы включает следующие этапы:

123
1.
По виду передаточной функции исходной системы
(
)
0
Ws
строится ЛАХ
исходной системы
(
)
0
ω
L . При этом исходная система должна иметь
функционально необходимые элементы и должна быть минимально-фазовой.
2.
На основании требований к САУ строится желаемая ЛАХ
()
ж
L
ω
.
3.
Путем сравнения характеристик
()
ж
L
ω
и
0
()
L
ω
определяется
()
К
L
ω=
0
()()
ж
LL
=ω−ω
(если коррекция последовательная). Эту коррекцию также
можно пересчитать к параллельной или встречно-параллельной.
4.
По виду
()
К
L
ω
определяется структурная схема и параметры
коррекции.
5.
Производится моделирование системы на ЦВМ (например в среде
Matlab), уточняются параметры САУ.
6.
Производится реализация коррекции с помощью регуляторов или
программно.
Построение ЛАХ исходной системы не вызывает затруднений. Рассмотрим
подробнее построение желаемой ЛАХ.
Учет требований точности САУ:
а) Пусть даны рабочая частота
ω
р
и амплитуда
p
υ
задающего воздействия
()
t
υ
, а также допустимая ошибка
доп
e
.
Так как для низких частот
( )
( )
ω
ω
e
Wj
υ
∆≅
, то при
ωω
р
=
,
p
υυ
=
(
)
(
)
ωω
р
WjWj
=
. Тогда
( )
ω
p
р
доп
KWj
e
υ
υ
=≥. (9.15)
б) Пусть даны
maxmax
,,
доп
e
υυ
&&&
. Тогда
( )
22
maxmaxmax
maxmaxmax
ω , , ω .
р p р
доп
KWj
e
υ
υυυ
υ
υυυ
===≥
&&&&
&&&&&
(9.16)
в) Пусть для астатической САУ даны
maxmax
υ
=Ω
&
и
доп
e
.
Тогда
( )
ν
ω
ωe
K
∆= и при
ν 1
=
( )
ω
ωe
K
∆=
и
max
доп
K
e
υ
Ω
≥ . (9.17)
С помощью выражений (9.15)–(9.17) строится низкочастотная область
()
ж
L
ω
(рис. 9.6).

124
ω
р
1
ω
2
ω
ω 1
=
K
υ
20
−
20lg
K
υ
(
)
ω
ж
L
ω
(
)
20lg
ω
р
Wj
Рис. 9.6
Значение частоты
K
υ
1
с
называют добротностью САУ по скорости.
Первый излом
()
ж
L
ω
на частоте
1
ω
при однократном изломе (при изменении
наклона на
дБ
20
дек
− ) определяется как
1
ω
a
K
K
υ
= , где
2
max
2
ω
а
доп
K
e
Ω
==
2
1
с
называют добротностью системы по скорости; при двукратном изломе
1
ω 2
а
K
K
υ
= .
Учет требований качества переходного процесса: ,
σ
р
t , колебатель-
ности, запасов устойчивости. Эти показатели учитываются при формировании
среднечастотной области
()
ж
L
ω
. Здесь можно воспользоваться графиками
(рис. 9.7, а, б).
−
−
−
−
−
−
−
−
−
−
m
P
π
ω
n
3
π
ω
n
5
π
ω
n
π
ω
р
K
n
t =
а
р
t
σ
−
−
−
−
−
−
2
L
′
∆ϕ
σ,%
1
2
,дБ
L
0
,
∆ϕ
б
σ,%
Рис. 9.7
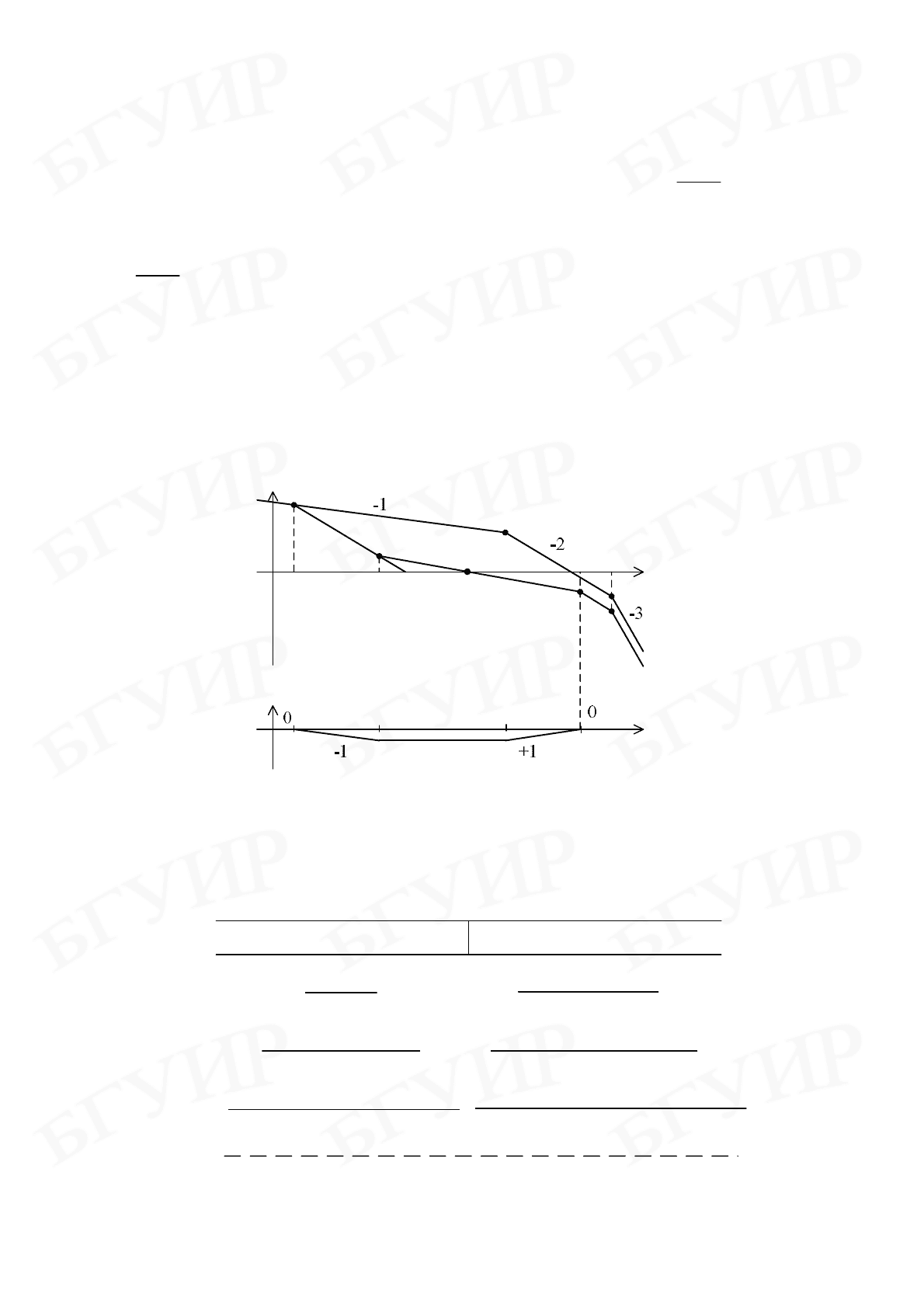
125
По графику (см. рис. 9.7, а) для заданных значений
σ
и
р
t
находят
ω
n
и
затем из соотношения
(
)
ω 0,60,9 ω
cn
≅
K
частоту среза
ω
с
.
Например: (как показано на рис. 9.7, а) для
σ 30%
=
,
4,7
π
ω
р
n
t ≈ , откуда для
заданного значения
р
t
(допустим, что оно равно 0,01 с), определяются значения
1
4,7π
ω 160c
0,01
n
−
==
и
1
ω 0,8ω 128c.
nc
−
≈≅
По графику (см. рис. 9.7, б), где установлены зависимости
∆ϕ
от
σ
и
ординат
1
L
и
2
L
среднечастотной части
()
ж
L
ω
от
σ
, находят для заданного
значения
σ
необходимые
1
L
,
2
L
и
∆ϕ
.
Сопряжение среднечастотного участка с низкочастотным и
высокочастотным (рис. 9.8) должно быть таким, чтобы была проще коррекция и
изломы, по возможности, были однократными.
1
ω
2
ω
ω
с
3
ω
4
ω
ω
40
−
(
)
ω
L
(
)
ω
исх
L
(
)
ω
К
L
0
(
)
ω
К
L
ω
Рис. 9.8
Для облегчения процедуры синтеза коррекции вводятся типовые
передаточные функции исходной системы и соответствующие им передаточные
функции желаемой системы:
*
0
()
Ks
()
ж
Ks
(1)
ж
K
sTs
+
2
13
(1)
(1)(1)
ж
KTs
sTsTs
+
++
12
('1)('1)
ж
K
sTsTs
++
2
134
(1)
(1)(1)(1)
ж
KTs
sTsTsTs
+
+++
123
('1)('1)('1)
ж
K
sTsTsTs
+++
2
1345
(1)
(1)(1)(1)(1)
ж
KTs
sTsTsTsTs
+
++++
*
0
ж
KK
=
с учётом требований по точности;
12345
.
TTTTT
>>>>

126
Остановимся на коррекции. Вычитая из
()
ж
L
ω
ординаты
0
()
L
ω
, получим
().
К
L
ω
Вид ЛАХ коррекции соответствует случаю коррекции с опережением и
отставанием по фазе.
Передаточная функция коррекции будет с учётом обеспечения показателей
точности иметь вид
23
14
(1)(1)
(),
(1)(1)
KK
TsTs
WsK
TsTs
++
=
++
(9.18)
где
1234
1234
1111
, , , ,
ωωωω
TTTT====
1234
;
TTTT
>>>
0
,
K
K
K
K
υ
= причём
0
K
−
коэффициент передачи исходной системы.
Так как реализовать дифференцирующие звенья сложно, переходят к схеме
коррекции с использованием интеграторов. Для этого необходимо представить
(9.18) в виде
2
2323
2
1414
()1
()
()1
KK
TTsTTs
WsK
TTsTTs
+++
=
+++
2
2323
2
14
14
1414
()1
.
1
K
KTTsTTs
TT
TT
ss
TTTT
+++
=
+
++
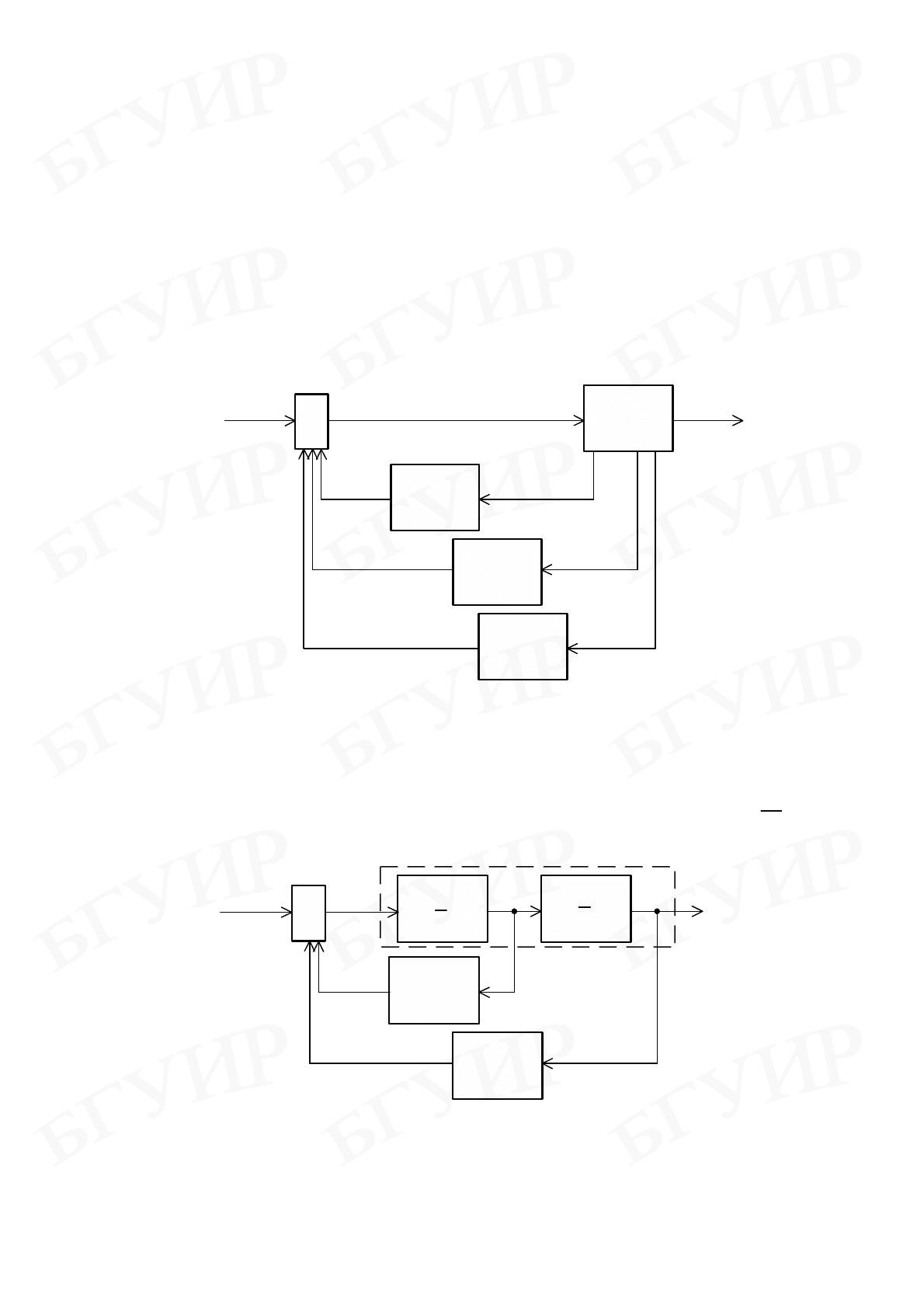
Схема реализации коррекции представлена на рис. 9.9.
+
e
1
s
14
1
TT
∑
14
14
TT
TT
+
1
s
∑
14
K
K
TT
23
TT
+
23
TT
+
+
+
u
−
−
Рис. 9.9
9.5. Модальный метод синтеза (метод размещения полюсов)
127
Рассмотрим САУ с одним входом и одним выходом, будем считать
0.
υ
=
Пусть модель объекта имеет вид
,
.
xAxBu
yCx
=+
=
&
(9.19)
При этом методе синтеза [6] закон управления выражается формулой
,
uKx
=−
(9.20)
где
K
−
вектор коэффициентов
[
]
12
.
n
kkk
K
Структура замкнутой САУ приведена на рис. 9.10.
+
0
υ
=
−
Oбъект
2
k
n
k
∑
u
1
k
−
−
y
ggg
n
x
1
x
2
x
Рис. 9.10
Так как
0,
υ
=
то назначение САУ поддерживать значение
0.
y
=
Такую
САУ называют регулятором состояния.
Рассмотрим пример спутника (рис. 9.11) с передаточной функцией
2
1
s
[6].
+
0
υ
=
1
s
1
k
2
k
∑
u
−
y
1
x
2
x
−
1
s
Cпутник
Рис. 9.11
Модель объекта (спутника) будет иметь вид

128
12
2
xx
xu
=
=
&
&
или
010
.
001
xxu
=+
&
Для замкнутой САУ, где
uKx
=−
, имеем
12
21122
xx
xkxkx
=
=−−
&
&
или
3
12
01
,
xxAx
kk
==
−−
&
(9.21)
где
3
A
−
матрица коэффициентов замкнутой САУ.
Характеристическое уравнение замкнутой САУ имеет вид
2
321
12
λ1
λλλ 0.
λ
EAkk
kk
−
−==++=
+
(9.22)
Пусть корни его будут
1
λ
−
и
2
λ
−
, тогда характеристическое уравнение
желаемой замкнутой системы имеет вид
2
1212
(
λ) λ (λλ)λλλ 0.
ж
D
=+++=
(9.23)
Синтез системы заключается в выборе
1
k
и
2
k
в (9.22), которые бы
соответствовали коэффициентам уравнения (9.23), т.е.
112
212
λλ ,
λλ.
k
k
=
=+
(9.24)
Рассмотрим общий принцип синтеза САУ.
Пусть
,
xAxBu
=+
&
(9.25)
,
uKx
=−
12
[]
n
Kkkk
=
K
.
(9.26)
Подставляя (9.26) в (9.25), получим
3
().
xAxBKxABKxAx
=−=−=
&
(9.27)
Характеристическое уравнение замкнутой САУ имеет вид
3
λλ 0.
EAEABK
−=−+=
(9.28)
Если корни
12
λ , λ , , λ ,
n
−−−
K
то желаемое характеристическое
уравнение замкнутой САУ будет иметь вид
1
121
(
λ)(λλ)(λλ)(λλ)λαλα0.
nn
nnж
D
−
=+++=+++=
KK
(9.29)
Приравнивая (9.28) и (9.29), имеем

129
1
1
λλαλα.
nn
n
EABK
−
−+=+++
K
(9.30)
В этом уравнении
n
неизвестных
12
(,,,),
n
kkk
K
но они могут быть
найдены путем приравнивания коэффициентов при
x
в одинаковых степенях.
Пусть передаточная функция объекта будет иметь вид
12
011
00
1
1
(), 1.
nn
n
nn
n
bsbsb
Wsa
sasa
−−
−
−
+++
==
+++
K
K
(9.31)
Уравнения состояния при
123
, , ,
yxxyxy
===
&&&
K
имеют вид
[ ]
120
121
01000
00100
, .
00010
1
nn
nnn
xxybbbx
aaaa
υ
−−
−−
=+=
−−−−
L
L
&
MMMMMMK
L
L
(9.32)
Матрица
A
является фробениусовой, а уравнение объекта соответствует
нормальной форме.
При законе модального уравнения
uKx
=−
для замкнутой САУ в
матрице
ABK
−
член
[ ]
12
12
0
000
0
.
1
n
n
BKkkk
kkk
==
L
KMMM
M
Матрица
3
11
0100
0010
.
0001
nn
AABK
akak
=−=
−−−−
L
L
LLL
Характеристическое уравнение замкнутой САУ имеет вид
[
]
1
1121
λλ()λ ()λ()0.
nn
nnn
EABKakakak
−
−
−+=+++++++=
K
Желаемое характеристическое уравнение замкнутой САУ будет
1
1
(
λ) λαλα0.
nn
nж
D
−
=+++=
K
Из двух последних уравнений следует:
1
11
α ,
α ,
nn
n
ak
ak
=+
=+
LLLLL
откуда
откуда
LLL
1
11
α ;
.
α .
nn
n
ka
ka
=−
=−
LLLLL
(9.33)

130
Последняя система представляет собой общее решение задачи синтеза
путём размещения полюсов для САУ с одним входом и одним выходом, но для
этого исходная модель САУ должна быть в нормальной форме (матрица
A
−
фробениусова).
Аккерман предложил формулу, которая позволяет перейти от
произвольной формы уравнений состояния к нормальной, затем найти
,
i
k
а
потом перейти к исходной структуре.
Формула Аккермана имеет вид
[ ]
1
21
0001(),
nn
ж
KBABABABDA
−
−−
=
KK (9.34)
где
()
ж
DA
−
матричный полином, образованный путём использования
коэффициентов желаемого характеристического уравнения
1
11
()
ααα.
nn
nnж
DAAAAE
−
−
=++++
K
(9.35)
Последние выражения (при
3
n
>
) рассчитываются на компьютере.
Пример 9.3. Для спутника
010
;
001
xxu
=+
&
характеристическое
уравнение
2
1212
(
λ) λ (λλ)λλλ 0.
ж
D
=+++=
Используем формулу Аккермана. Определим
0101
,
0010
AB
==
затем
[
]
1
BAB
−
=
1
0101
1010
−
=
. Образуем матричный полином
2
12121212
01010110
()(λλ) λλ (λλ) λλ
00000001
ж
DAAAE
=+++=+++=
12121212
1212
λλ 0 λλλλ
000λλ
.
0 λλ 0 λλ
0000
++
=++=
По формуле Аккермана
[ ][ ] [ ]
1
1212
12
λλλλ
01
01()01
0 λλ
10
ж
KBABDA
−
+
===
[ ] [ ]
12
1212
1212
0 λλ
01
λλλλ.
λλλλ
==+
+
Как видим, результаты совпали с (9.24).
Остановимся на вопросе формирования полюсов передаточной функции
замкнутой САУ, исходя из заданных показателей качества на основе корневых
оценок.
