Кузнецов О.Л., Никитин А.А., Черемисина Е.Н. Геоинформатика и геоинформационные системы
Подождите немного. Документ загружается.

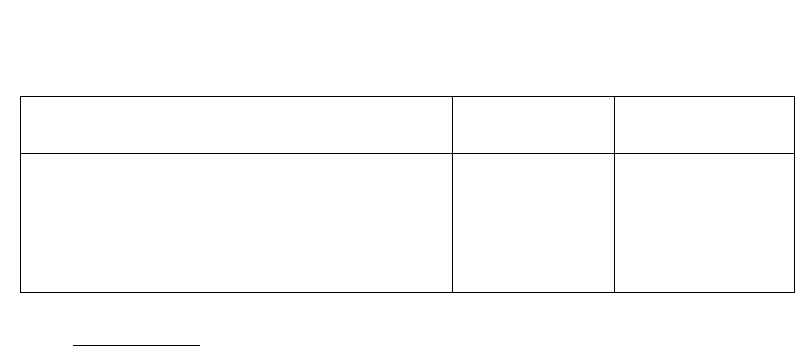
Таблица 9
Надежность литологического расчленения по данным геофизиче-
ских исследований скважин.
Комплекс Надежность
Соответствие
выходу керна
КС + ГК
КС + ГК + ГГК
КС + ГК + ГГК + АК
КС + ГК + ГГК + АК +КС
ГЗ
КС + ГК + ГГК + АК +КС
ГЗ
+ИННК
0,350
0,705
0,865
0,897
0,967
0,86
0,96
0,977
1,000
Примечание: КС
ГЗ
– каротаж сопротивлений по градиентзондам; КС
– каротаж сопротивлений по потенциал-зондам; ГК – гамма-каротаж; ГГК –
гамма-гамма-каротаж; АК – акустический каротаж; ИННК – импульсный
нейтрон-нейтронный каротаж.
Отличительной особенностью этой АСОД являются использование
комплексных петрофизических моделей, выраженных многомерными урав-
нениями регрессии для оценки показателей качества углей и физико-
механических свойств пород.
Для решения задач литологического расчленения разрезов скважин,
выделения типов углей, водоносных и газоносных горизонтов реализуются
методы распознавания образов, а задачи пространственного моделирования
геологических тел решаются путем аппроксимационных алгоритмов.
Система АСОД – Углеразведка была внедрена на предприятиях До-
нецкого, Кузнецкого, Канско-Ачинского и Улуг-Хемского угленосных бас-
сейнов.
Для комплексной интерпретации данных сейсморазведки и гравираз-
ведки с целью картирования фундамента и других опорных горизонтов до
сих пор применяется система АСКИНТ (автоматизированная система ком-
плексной интерпретации), созданная в объединении «Центргеофизика»
(В.С. Славкин, П.А. Беспрозванный). В системе используется регрессионная
зависимость между данными гравиразведки ∆g
i
глубинами структурных
планов Н
i
, полученных сейсморазведкой, вида Н
i
= a
0
+ a
1
∆
g
i
. Коэффициен-

ты регрессии a
0
, a
1
определяются на участках, на которых имеются данные о
глубинах опорных горизонтов, а прогноз глубины залегания осуществляется
при их отсутствии непосредственно по данным гравиразведки.
Использование нелинейной зависимости между данными метода об-
щей глубинной точки t
0
и данными зондирования становлением поля в
ближней зоне t
ЗСБ
в виде t
0
= а
ЗСБ
t
заложено в автоматизированной сис-
теме СЭВР для построения сейсмоэлектрических временных разрезов. Сис-
тема создана
в НВНИИГГ (Н.П. Смилевец и др.).
Ряд АСОД комплексного анализа был построен на использовании
мер сходства эталонных объектов с искомыми объектами в виде «потенци-
альных» функций. Так, в системе «ПОТЕНЦИАЛ» (ВИМС, И.Д. Савин-
ский) для каждого искомого объекта в L – мерном пространстве признаков
(полей) вычисляется «потенциал»
( )
∑
∑
=
=
−
=
k
n
k
lkl
L
l
l
k
k
xxh
k
n
V
1
2
1
1
α
,
где X
kl
и X
l
– значения l-го признака k-го объекта обучения и искомого объ-
екта; n
k
– число объектов обучения k-го класса; α
k
и h
l
– «веса» k-го объекта
обучения и l-го признака, определяемых на эталонных объектах. Искомый
объект относится к тому классу, «потенциал» (мера сходства) которого бу-
дет большим, чем для других классов.
Методы проверки статистических гипотез по формуле Байеса
использованы в АСОД комплексного анализа РЕГИОН (МНИИПУ, В.В.
Марченко, Г.А. Чумаченко) удостоенной госпремии СССР в 1989 г. и КОС-
КАД-3D (МГГРУ, А.В. Петров, А.А. Никитин), реализованные на персо-
нальных компьютерах под ОС WINDOWS.
При распознавании объектов двух классов, что соответствует сравне-
нию двух статистических гипотез Н
1
(руда) и Н
2
(«вмещающая порода»)

достаточно ограничиться вычислением коэффициента правдоподобия. Для
независимых признаков коэффициент правдоподобия равен отношению
плотности распределения значений признаков, оценками которых служат
гистограммы P(X
l
/H
k
), вычисляемые для каждого l-го признака и по каждо-
му k-му классу. Для двух классов коэффициент првдоподобия:
( ) ( ) ( )
( ) ( ) ( )
22221
11211
/...//
/...//
HxPHxPHxP
HxPHxPHxP
L
L
x
=
Λ
→
.
Значения частных коэффициентов правдоподобия
Λ
(x
l
)=P(x
l
/H
1
)/P(x
l
/
H
2
) характеризуют относительный вклад каждого признака в общую вели-
чину Λ(
x
→
). Эти значения определяют количественную оценку информатив-
ности признаков.
Распознавание искомых объектов сводится к нахождению в i-ой точ-
ке (ячейке) значений Р(x
li
/H
1
) и Р(x
li
/H
2
), которые снимаются с гистограмм,
построенных для эталонных объектов каждого класса. После этого рассчи-
тывается величина
Λ
(
x
→
). Отметим, что ограничения на законы распределе-
ния признаков здесь отсутствуют, не требуется и задание априорных веро-
ятностей каждого класса. Решение о принадлежности i-го объекта к классу
Н
1
принимается согласно критерию максимального правдоподобия
при
Λ
(
x
→
)>1,при
Λ
(
x
→
)<1, – справедлива гипотеза H
2
, т.е. объект принадлежит
ко второму классу.
На основе формулы Байеса по найденному коэффициенту правдопо-
добия может быть вычислена апостериорная вероятность гипотезы H
1
:
( )
( )
12
1
12
/
/,
/1
i
i
i
pp x
pH x
pp x
→
→
→
Λ
=
Λ+
где р
1
и р
2
– априорные вероятности классов Н
1
и Н
2
.
Приняв р
1=
р
2
, что соответствует максимальной неопределенности
классов, получаем правило решения для апостериорной вероятности в виде
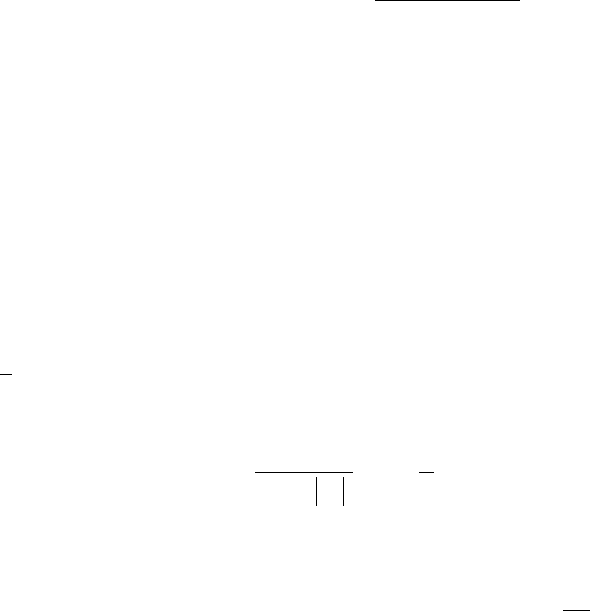
1
/ 0,5
i
pH x
→
>
, т.е. выполняется гипотеза Н
1
, а при
1
/ 0,5
i
pH x
→
<
будет
справедлива гипотеза H
2
.
При распознавании объектов на число классов, большее двух (М>2),
вычисления проводятся непосредственно по формуле Байеса.
1
(/ )
/.
/
i
k
ki
M
i
kk
k
ppx H
pH x
pP x H
α
→
→
→
=
=
∑
При этом для каждого класса последовательно находятся значения
12
/ , / ..., /
i i Mi
pH x pH x pH x
→→ →
и для максимального из них принимается
решение о принадлежности i- ой точки (ячейки) к тому или иному классу.
При распознавании объектов для зависимых между собой признаков
исходят из предположения об их нормальном распределении оценивают
корреляционные матрицы R
k
, которые стоятся по каждому классу в отдель-
ности. При этом многомерная плотность распределения вектора признаков
( )
L
xxx ,...,
1
=
для класса Н
k
определяется выражением:
( )
−
−−=
→→
−
→→→
kikki
k
ki
xRx
R
Hxp
µµ
π
1
2/1
2
1
exp
2
1
/
где
1−
k
R
– матрица, обратная матрице R
k
; |R
k
| – определитель матрицы;
k
µ
→
–
вектор средних значений признаков k-го класса;
ik
x
µ
→
′
−
и
ik
x
µ
→→
−
– век-
тор-строка и вектор-столбец.
Используя формулу Байеса, решение о принадлежности объекта к
тому или иному классу принимают по максимальной величине апостериор-
но вероятности из М чисел
/
ki
pH x
→
, к = 1,…, М.
Приведенные алгоритмы реализованы в системе КОСКАД-3D в виде
многомерных аналогов способа обратных вероятностей, в основе которого
заложена формула Байеса (см. раздел 10.3).

Среди АСОД комплексного анализа при отсутствии эталонных объ-
ектов наиболее распространенными являются системы КОМПАК («Иркут-
скгеология», В.В. Ломтадзе), КОСКАД-3D (МГГРУ, А.В. Петров, А.А. Ни-
китин) и ПАНГЕЯ (ЗАО «ПАНГЕЯ»), прообразом последней явилось АС
ГЕОКОМПАС (ВНИИГеофизика, Э.Ю. Миколаевский). Во всех этих систе-
мах широко используются методы факторного анализа, в частности, метод
главных компонент. Метод главных компонент, известен также как метод
естественных ортогональных функций, впервые в геофизике вначале 70-х
годов прошлого столетия был реализован П.Н. Горбуновым. Для его реали-
зации по исходным геофизическим полям рассчитываются вторичные при-
знаки в скользящих окнах. Комплекс таких признаков чаще всего содержит:
статистические (среднее, дисперсия, коэффициент вариации, асимметрия,
эксцесс), градиентные (производные по x и по y, полный градиент, направ-
ление полного градиента, крутизна изолиний), корреляционные (интервал
корреляции, отношение сигнал/помеха
22
/
σ
S
, вычисляемое по величине
положительного экстремума нормированной взаимнр корреляционной
функции B
H
(l
э
) данных соседних пар профилей (трасс), т.е.
( ) ( )( )
эHэH
lBlBs −= 1//
22
σ
и спектральные (видимый период, ширина спек-
тра) характеристики.
По комплексу исходных значений геофизических полей и их вторич-
ных характеристик x
j
(j=1,…,n) строится корреляционная матрица, для кото-
рой находятся собственные значения и соответствующие им собственные
вектора.
Для максимального собственного значения λ max и соответствующе-
го ему собственного вектора a
1j
, координаты которого являются весовыми
коэффициентами для каждой характеристики (признака), находятся значе-
ния первой главной компоненты
j
n
j
xaY
j
∑
=
=
1
11
, n – число характеристик.
Физический смысл первой главной компоненты определяется оцен-
кой энергетического отношения сигнал/помеха в пространстве комплекса
изучаемых характеристик (признаков), иначе максимальные значения пер-
вой главной компоненты выделяют участки (площади) с наибольшей энер-
гией (дисперсией) в комплексном пространстве, которые обычно и пред-
ставляют прогнозно-поисковый интерес. Далее рассчитывается вторая глав-
ная компонента, соответствующая второму по величине собственному зна-
чению корреляционной матрицы исходных характеристик и т.д. Обычно ог-
раничиваются расчетом двух – трёх главных компонент, которые, по суще-
ству, выбирают всю энергию исходных данных. Так, первая главная компо-
нента, как правило, обеспечивает от 70 до 90% всей энергии в пространстве
данных.
Составляя систему координат из первых трех главных компонент,
нередко удается найти геологическое истолкование (геологическую привяз-
ку) или физический смысл каждой компоненты.
Отличительной особенностью системы КОСКАД-3D является ис-
пользование оригинальных алгоритмов классификации объектов по ком-
плексу признаков, реализующих многомерный аналог способа самонастраи-
вающейся фильтрации и модифицированный алгоритм метода К-средних
(А.В. Петров).
Метод К-средних (или метод динамических сгущений) предложен Д.
Мак-Куином и был впервые реализован А.Н. Кленчиным для решения задач
районирования по комплексу геофизических методов. Его суть состоит в
следующем. Множество исходных точек наблюдений, охарактеризованное
комплексом различных признаков разбивается на заданное число классов
М<<n. Сначала датчиком случайных чисел выбирается М точек из общей
совокупности наблюдений. Эти случайно выбранные точки (объекты) явля-
ются нулевым приближением
( )
ii
xe =
0
с весами
( )
1
0
=
i
h
, i = 1,…,k.

Затем извлекается объект (точка) x
k+1
и выясняется, к какому из эта-
лонов
( )
0
i
e
он оказался ближе всего по расстоянию в L – мерном пространст-
ве признаков:
( )
( )
∑
=
−=
L
l
likli
ex
1
2
0
,
ρ
, i = 1,…,k. Тогда эталон заменяется но-
вым, определяемым как «центр тяжести» старого эталона и присоединенно-
го к нему объекта x
k+1
с увеличением на единицу соответствующего ему ве-
са. Пересчет эталонов и соответствующих им весов на ν-ом шаге проводится
по формуле
( )
( ) ( )
( )
1
1
0
+
+
=
+
−
ν
ν
νν
i
kii
i
h
xeh
e
, где
( ) ( )
1
1
+=
−
νν
ii
hh
, при условии, что рас-
стояние ρ между
ν
+k
x
и
1−
ν
i
e
минимально.
И по формуле
( ) ( )
1−
=
νν
ehe
ii
;
( ) ( )
1−
=
νν
ii
hh
, если это условие не выполня-
ется.
Результаты классификации геофизических полей, приведенных на
рис.4.2, по методу К-средних на два (а), три (б), четыре (в) и пять (г) классов
изображены на рис. 4.3.
Метод К-средних предназначен для классификации объектов по ком-
плексу независимых между собой признаков. Его модификация для зависи-
мых признаков была реализована А.В. Петровым в системе КОСКАД-3D
(см. раздел 10.5).
Суть модификации заключается в том, что для первоначально прове-
денной классификации по методу К-средних без учета зависимости призна-
ков, оценивается корреляционная матрица признаков по данным этой клас-
сификации.
Далее проводится реклассификация исследуемой площади и осуще-
ствляется заново классификация площади, но уже с известной корреляцион-
ной матрицей. Последняя процедура обеспечивает оценку качества класси-
фикации путем общего, межклассового и внутриклассового разбросов и оп-
ределение количества образованных кластеров – однородных по комплексу
признаков областей.
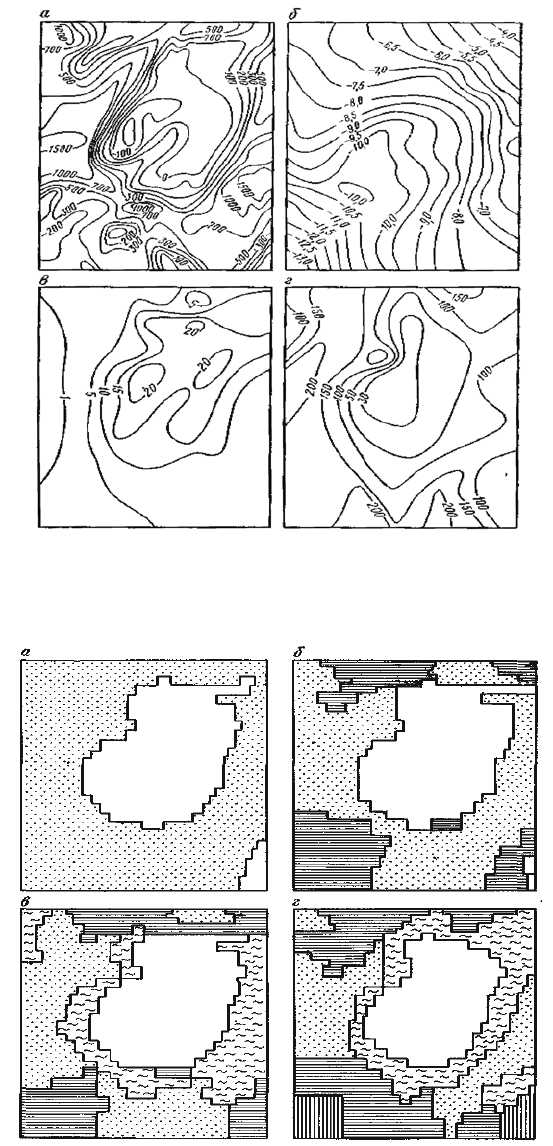
Рис.4.2. Геофизические поля над Бенкалинским меднопорфировым место-
рождением а – Zα в нТл; б –∆g вусл. Ед.; в – η
κ
в %; г – ρ
k
в Ом м.
Рис. 4.3. Результаты классификации геофизических полей, приведенных на
рис.4.2.
4.4 Автоматизированные рабочие места и полевые
вычислительные комплексы
Появление персональных компьютеров привело к концепции автома-
тизированного рабочего места для геологов и геофизиков.
Автоматизированное рабочее место (АРМ) в соответствии с тер-
минологией систем автоматизированного проектирования (САПР)
представляет программно технический комплекс автоматизированного про-
ектирования, предназначенный для выполнения следующих функций: 1)
оперативного ввода – вывода, редактирования и преобразования текстовой и
(или) графической информации; 2) редактирования, исполнения и контроля
программ пользователей в диалоговом режиме; 3) формирования библиоте-
ки прикладных программ; 4) осуществления взаимодействия с другими
АРМ и с центральным вычислительным комплексом. Таким образом, АРМ,
по существу, выполняет основные функции автоматизированных систем об-
работки данных. Обычно в АРМ входит персональный компьютер или рабо-
чая станция с графическими и (или) текстовым дисплеем, графопостроите-
лем и другие периферийные устройства. АРМ работает либо в автономном
режиме, либо в составе локальной сети.
Полевой вычислительный комплекс (ПВК) представляет передвиж-
ной вариант АРМа.
АРМ, в зависимости от используемых программных продуктов, так-
же, как и АСОД, подразделяют на методно-ориентированные и проблемно-
ориентированные.
При создании АРМ геолога и геофизика (АРМ-Гео) следует учиты-
вать специфику геоинформации и решения геологоразведочных задач. Сре-
ди основных принципов построения АРМ-Гео можно выделить следующие:
– необходимость построения стационарных и передвижных АРМ,
поскольку геологоразведочный процесс характеризуется чередовани-
ем двух разделенных как территориально, так и во времени циклов:
камерального и полевого. При камеральном цикле анализируются и
обобщаются большие объемы разнородной информации, строятся
физико-геологические модели изучаемых объектов, при полевом
цикле следует обеспечить высокую производительность работ при
заданной точности и непрерывной корректировке методики наблю-
дений. Эти различия и определяют необходимость создания как ста-
ционарных, так и передвижных АРМ. Передвижные АРМ, или ПВК,
используются непосредственно по месту проведения работ;
– целесообразность формирования персональных баз данных и знаний.
В геологоразведке существует определенная специализация геологов
и геофизиков по объектам (виды полезных ископаемых, типы место-
рождений, регионы и т.д.); по стадиям и задачам (картирование, про-
гноз и поиски, разведка, подсчет запасов и т.д.); по методам разве-
дочной геофизики. В процессе проведения работ, чтения специаль-
ной литературы, участия в семинарах и конференциях у каждого спе-
циалиста (геолога, геофизика) формируется персональная база дан-
ных и знаний, являющаяся основой построения соответствующих
АСОД и экспертных систем (гл. VIII);
– непрерывное развитие программного обеспечения АРМ и ПВК за
счет совершенствования вычислительной техники, диалоговых и
графических средств, что позволяет использовать в настоящее время
современные алгоритмы и программы обработки и комплексного
анализа геоданных. В свою очередь это обстоятельство открывает
принципиально новые возможности моделирования геообъектов и
геопроцессов на базе АРМ-Гео;
– создание экспертных систем на базе АРМ и ПВК. Этот принцип яв-
ляется развитием двух предыдущих, он обусловлен также слабой
формализацией знаний в геологоразведке. Слабая формализация
большинства понятий в геологии препятствует широкому примене-
нию в ней АСОД в отличие от разведочной геофизики. Кроме того,
