Курсовой проект - Рототабельное планирование второго порядка с разработкой математических моделей и оптимизацией двухфакторного процесса с двумя выходными параметрами
Подождите немного. Документ загружается.

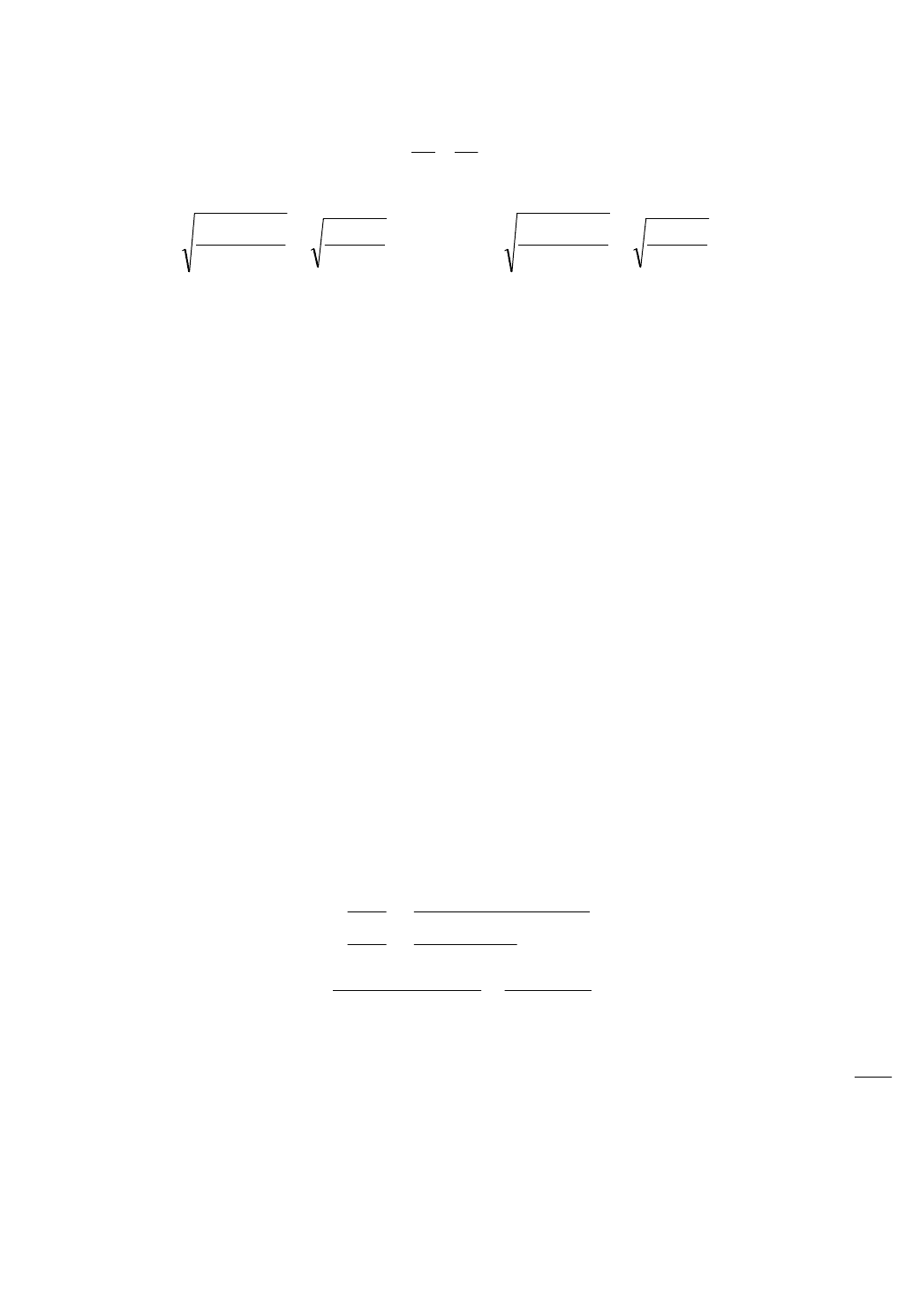
Для построения линий равного отклика функции
Q
y
, соответствующей
max
Q
y
=55.813
мм/мин, подставим это значение в каноническое уравнение
Q
y
:
2
2
2
1
max
838.10162.17605.37208.18813.55208.18 XXy
Q
Приводим уравнение к канонической форме эллипса:
1
2
2
2
2
2
1
b
x
a
x
,
где полуоси эллипса a и b равны:
291.1
854.17
452.36
11
max
B
yy
a
QsQ
;
624.1
146.11
452.35
22
max
B
yy
b
QsQ
Кодированные значения полуосей переводим в мм:
ммaa 283.3225*291.125*'
;
ммbb 6.4025*624.125*'
. Откладываем полуоси на координатных осях: a’ – на оси X
1
;
b’ – на оси Х
2
. Проводим через точки a’А
1
b’ четвертинку эллипса, представляющего
собой линию равного отклика функции
Q
y
, соответствующую наибольшей
производительности
max
Q
y
= 55.813 мм/мин, которая обеспечивается на режимах
1
А
Э
=11.25 мДж,
1
А
f
=41 кГц при ограничении по износу электрода-инструмента y
=33%.
Наименьшая производительность
min
Q
y
при соблюдении требований по износу y
=33%
соответствует случаю, когда линия равного отклика функции y
Q
будет представлена
наименьшим по размеру эллипсом, но имеющим общую точку с построенной линией
равного отклика для y
(отрезок параболы A
1
, A
2
, A
3
) в пределах факторного
пространства. Очевидно это будет точка касания эллипса и параболы в I квадранте
системы координат х
1
Ох
2
. Для определения координат точки касания от обеих частей
уравнений регрессии обеих y
Q
и y
берем дифференциалы по х
1
и
х
2
: (если
)(xfy
, то
dxxfdy *)('
)
а) исходные уравнения:
2
2
2
12121
15136191025 xxxxxxy
Q
2
221
98830%33 xxxy
б) после дифференцирования
01888
03026661910
2221
2211122121
dxxdxdx
dxxdxxdxxdxxdxdx
После преобразования получим:
)188(8
)30619()26610(
221
212121
xdxdx
xxdxxxdx
8
188
26610
30619
2
2
1
12
21
2
1
x
dx
dx
xx
xx
dx
dx
8
188
26610
30619
2
12
21
x
xx
xx
Равенство правых частей уравнений вытекает из того, что в точке касания двух
кривых у них общая касательная и, следовательно, tg угла наклона касательной
2
1
dx
dx
одинаковый для обеих кривых.
Освобождаемся от знаменателей
2121
2
221221
306195.585.135.222661030619 xxxxxxxxxx
Приводим подобные:
05.135.585.46209
2
22121
xxxxx
Сократим на 20:
0675.0925.2325.245.0
2
22121
xxxxx
21
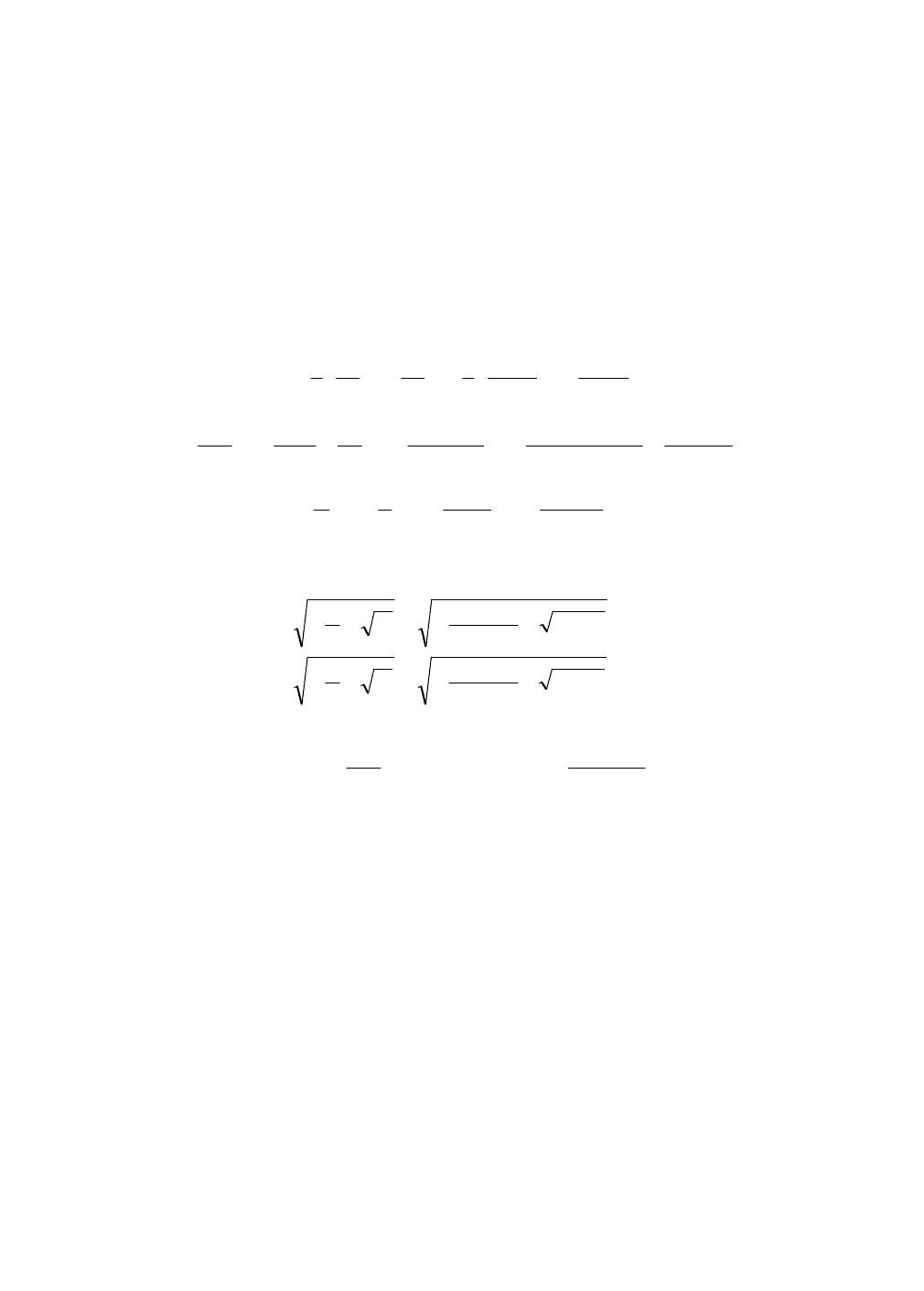
Получили уравнение линии точек касания эллипса y
Q
и параболы y
при различных
сочетаниях конкретных ограничений параметрам.
Так как одна из точек касания принадлежит и параболе
2
221
9883033 xxxy
,
выразим х
1
через
х
2
:
375.0125.1
2
2
21
xxx
Подставим х
1
в полученное уравнение лини точек касания:
0675.0*375.0125.1*925.2325.2375.0125.145.0
2
222
2
222
2
2
xxxxxxx
После упрощения получим:
0825.0228.2375.3291.3
2
2
2
3
2
xxx
Получили полное кубическое уравнение вида:
0
32
2
1
3
axaxaxa
o
. В нашем уравнении:
825.0;228.2;375.3;291.3
321
aaaa
o
.
Определяем корни кубического уравнения по формулам Кардано. Для этого вычислим
коэффициенты Кардано p, q, Q:
326.0
291.3
228.2
291.3
375.3
3
1
3
1
2
2
2
1
oo
a
a
a
a
p
402.0
291.3
825.0
291.3*3
228.2*375.3
291.3*3
375.3
2
3
3
2
2
3
3
2
0
21
3
1
oo
a
a
a
aa
a
a
q
042.0
2
402.0
3
326.0
23
2323
qp
Q
Так как. Q<0, то кубическое уравнение имеет только один действительный корень и
для его нахождения определяют коэффициенты А и В:
1579.0042.0
2
402.0
2
7404.0042.0
2
402.0
2
33
33
Q
q
B
Q
q
A
Тогда действительный корень равен:
2512.0
291.3*3
375.3
1579.07404.0
3
0
1
2
a
a
BAx
Корень уравнения
2512.0
2
x
лежит в пределах факторного пространства +1…-1.
Подставляя
2
x
в уравнение параболы находим вторые координаты точек касания:
0328.0375.02512.02512.0*125.1375.0125.1
2
2
2
21
xxx
Таким образом, искомые координаты точки касания искомого эллипса,
соответствующего случаю
min
Q
y
при y
=33%, и параболы, представляющей линию
равного отклика функции
2
221
98830%33 xxxy
, имеют следующие значения:
2512.0;0328.0
21
xx
. На графике это точка С.
Подставляя найденные
1
x
и
2
x
в уравнение
Q
y
, находим наименьшую
производительность при износе электрода-инструмента y
=33%:
минмм
xxxxxxy
Q
/761.202512.0*150328.0*13
2512.0*0328.0*62512.0*190328.0*102515136191025
22
2
2
2
12121
min
Для графического изображения двумерного сечения поверхности отклика функции
Q
y
,
соответствующего случаю
min
Q
y
при y
=53%, подставим значение в каноническое
уравнение
Q
y
:
2
2
2
1
min
838.10162.17208.18 XXy
Q
2
2
2
1
838.10162.17553.2208.18761.20 XX
22
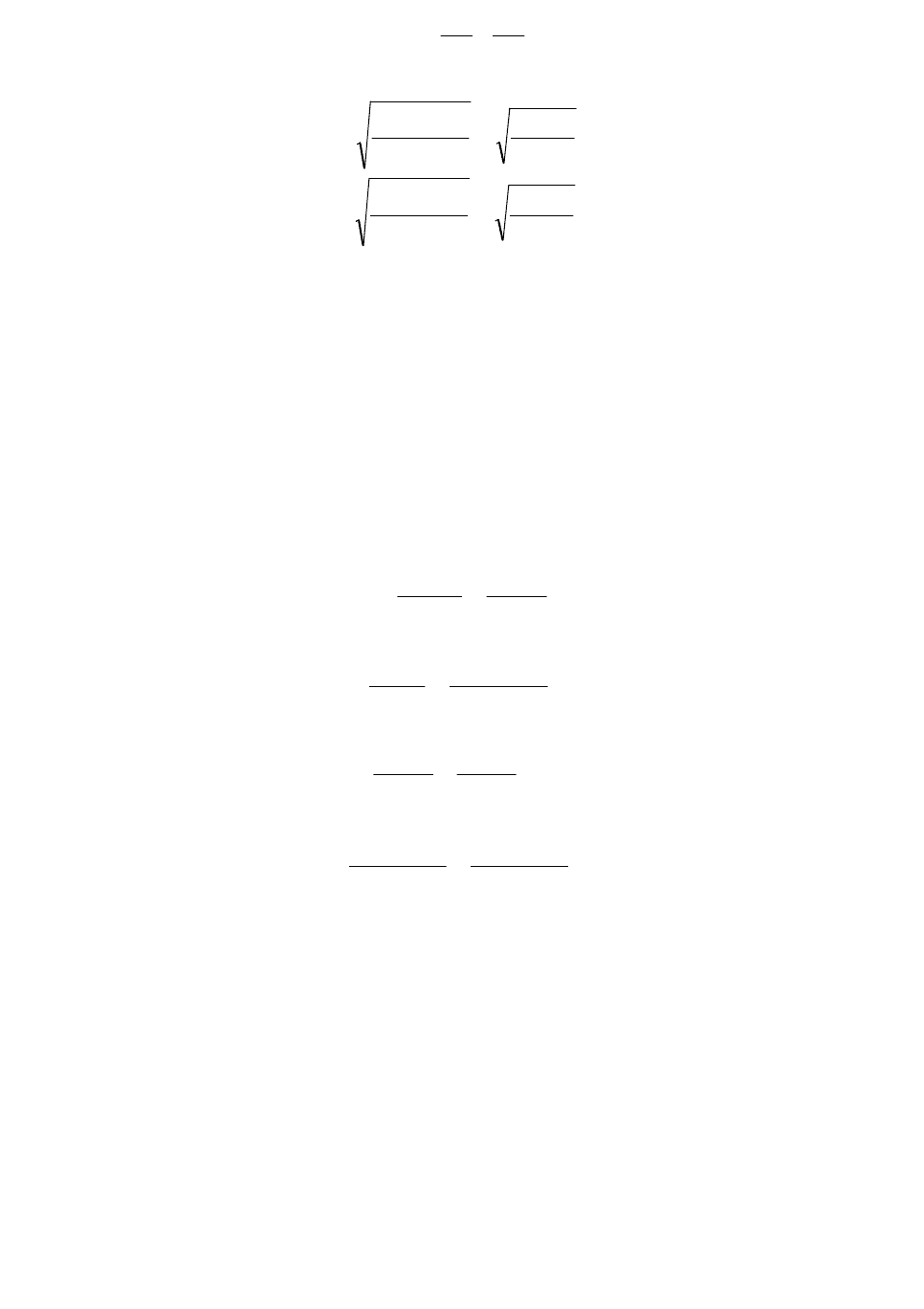
Приводим уравнение к канонической форме эллипса
1
2
2
2
2
2
1
b
X
a
X
,
где полуоси a и b равны:
386.0
162.17
553.2
11
min
B
yy
a
S
QQ
485.0
838.10
553.2
22
min
B
yy
b
S
QQ
Кодированные значения осей переводим в мм:
ммaa 642.925*386.025*
ммbb 134.1225*485.025*
Откладываем полуоси на координатных осях:
a
– на оси Х
1
;
b
– на оси Х
2
. проводим
через точки
bca
четвертинку эллипса, представляющую собой линию равного отклика
функции
Q
y
, соответствующую наименьшей производительности процесса
минммy
Q
/761.20
min
при y
=33%.
Определяем натуральные значения режимов обработки, соответствующие
min
Q
y
при
y
=33%, т.е. точке С на графике, через формулы перехода.
Для энергии импульсов тока:
22.0
5
10
0
1
Э
Э
Э
ЭЭ
x
Откуда
мДж
x
Э
C
164.10
2.0
20328.0
2.0
2
1
Для частоты импульсов:
864.2045.0
22
63
0
2
f
f
f
ff
x
Откуда
кГц
x
f
C
2267.69
2.0
20328.0
045.0
864.2
2
Таким образом, при требовании по относительному износу электрода-инструмента
33% максимальная производительность электроэрозионной прошивки отверстий
обеспечивается на режимах: энергия импульсов тока Э=11.25 мДж, частота импульсов
f=41кГц и составляет
max
Q
y
= 55.813 мм/мин. Наименьшая производительность
составляет
минммy
Q
/761.20
min
и обеспечивается на режимах: Э=10.164 мДж и f=69.2267
кГц.
23
