Курсовой проект - Рототабельное планирование второго порядка с разработкой математических моделей и оптимизацией двухфакторного процесса с двумя выходными параметрами

Подождите немного. Документ загружается.

731.1891.14

731.1642.12

284.275.5

615.1816.18

615.1251.10

042.2184.25



то уравнение регрессии полученное в результате рототабельного планирования

второго порядка, примет вид:

12121

891.14642.1275.5816.18251.10184.25 xxxxxxy



Адекватность полученной модели проверяем с помощью f-критерия:

 

ад





где

ад



- дисперсия адекватности;

 



=3.075 – дисперсия выходного параметра.

Дисперсию адекватности определяем по выражению

ад







где число степеней свободы

3)15(613)1('

 nkNf

; где k’=6 – число значимых

коэффициентов модели; N=13 – общее число опытов, n

=6 – число опытов в центре

плана.

 







yyS

- сумма квадратов отклонений экспериментальных значений

параметра

от среднеарифметического

по результатам 5-ти опытов в центре

плана (см. раздел 1).

         

8.102.25262.25242.25272.25232.2526

222























yyS

– сумма квадратов отклонений расчетных



значений функции

отклика от экспериментальных

во всех точках плана. Для расчета

составим

вспомогательную таблицу 9.

Таблица 9

№

оп.

12121

891.14642.1275.5816.18251.10184.25 xxxxxxy





















4003.29891.14642.1275.5816.18251.10184.25





29 0.1602

4018.38891.14642.1275.5816.18251.10184.25





38 0.1614

5323.55891.14642.1275.5816.18251.10184.25





56 0.2188

5338.87891.14642.1275.5816.18251.10184.25





88 0.2174

9739.350642.12*200251.10*414.1184.25





36 0.0007

963.640642.12*200251.10*414.1184.25





65 0.0014

3498.28891.14*200816.18*414.10184.25





29 0.4099

5714.81891.14*200816.18*414.10184.25





81 0.3266

184.2500000184.25





26 0.6654

184.2500000184.25





23 4.7709

184.2500000184.25





27 3.2969

184.2500000184.25





24 1.4024

184.2500000184.25





26 0.6654

297.12

Тогда

4992.0

8.10297.12







ад



Расчетное значение F – критерия:

 

1849.0

7.2

4992.0



ад



Табличное значение F

– критерия при 5%-ном уровне значимости и числе степеней

свободы для большей дисперсии (

 



)

4151

nf

, и для меньшей дисперсии

 

3)15(613)1('

 nkNf

ад



равно F

=9,1. Так как

< F

, полученная модель

адекватна.

Раскодируем уравнение регрессии для y

через формулу перехода:

;

ЭЭ













;

где x

и x

– кодированные значения факторов. Э

- натуральные значения факторов

основного уровня.

Э

f

- интервалы варьирования факторов. Э и f – натуральные

переменные значения факторов. После подстановки значений

Э

f

имеем:

;









Подставим формулы перехода x

и x

в уравнение регрессии:

031.0506.0052.0281.5446.15967.305

891.14

642.12

75.5

816.18

251.10184.25

fЭЭffЭ

ЭfЭfЭ















































Правильность раскодирования проверяем путем подстановки натуральных значений

факторов в полученное уравнение. Например опыт №1: x

=+1; Э

=15 мДж; x

=+1; f

=85

кГц; Q

э1

=29мм/мин

007.2985*031.015*506.085*15*052.085*281.515*446.15457.305



Раскодирование верно.

2.2. Вычисления для параметра



– относительного линейного износа электрода-

инструмента.

Определяем коэффициенты квадратичного полинома b

, b

Свободный член уравнения регрессии:















 

 

jij

yxcyk

1 1

2)2(2





Здесь А, λ, с – константы, табличные значения которых для к=2 и «ядра» плана в

виде ПФЭ 2

имеют значения А=0,492; λ=0,8125; с=1,625; N=13 – общее число опытов; y

–

экспериментальное значение параметра y

по всем 13 опытам;

- значение элементов

столбцов

. После подстановки числовых значений имеем:

181.30)]2*372*5.6124395.395.552*192*4124395.395.55(*625.1*

*8125.0*2)5.305.29322831375.61194124395.395.55(48125.0*2[

492.0



b

Коэффициенты при линейных членах:







763.7)414.1*1941*414.124395.395.55(

625.1









33.8)37*414.15.61*414.124395.395.55(

625.1



Коэффициенты при парных взаимодействиях:











25.0)24395.395.55(

8125.013

625.1

jjj

yxx





Коэффициенты при квадратичных членах:

 

















  



2)1()2(

jjij

ycyxcyxkkc





1312.0)}5.305.29322831375.61194124395.395.55(*

*625.1*8125.0*2)37*25.61*224395.395.5519*241*224395.395.55(*)8125.0

1(*625.1)19*241*224395.395.55(*]28125,0*)22[(*625.1{

492.0







 

















  



2)1()2(

jjij

ycyxcyxkkc





488.9)}5.305.29322831375.61194124395.395.55(*

*625.1*8125.0*2)37*25.61*224395.395.5519*241*224395.395.55(*)8125.0

1(*625.1)37*25.61*224395.395.55(*]28125,0*)22[(*625.1{

492.0







Дисперсия

 





выходного параметра



была определена по результатам 5 опытов

(№9…13) в центре плана и составила

 





=2.325. Определяем дисперсию

коэффициентов уравнения регрессии для параметра



Дисперсия свободного члена:

 

465.0325.2

)22(*8125.0*492.0*2)2(2



















Дисперсия коэффициентов при линейных членах:

 

291.0325.2

625.1







Дисперсия членов при парных взаимодействиях:

 

581.0

138125.0

2.325

*625.1















Дисперсия коэффициентов при квадратичных членах:

 

 

 

 

   

 

334.0325.2*

128125.0*12*625.1*492.0)1(1



















kkAc

Среднеквадратичные ошибки в определении коэффициентов уравнения регрессии

для

 





   

682.0465.0

 bb



   

539.0291.0





   

762.0581.0



ilil



   

578.0334.0



iiii



Определяем доверительные интервалы для коэффициентов:

 

895.1682.078.2

 btb



 

499.1539.078.2 

btb



 

119.2762.078.2 

ilil

btb



 

607.1578.078.2 

iiii

btb



где t=2,78 – табличное значение t – критерия Стьюдента при 5%-ном уровне

значимости и числе степеней свободы f=n

-1=5-1=4.

Из расчетов видно, что коэффициенты b

и b

по абсолютной величине меньше

соответствующих доверительных интервалов:

607.11312.0

119.225.0



Их можно признать статистически незначимыми и исключить из уравнения регрессии.

Тогда уравнение примет вид:

22222110

xbxbxbby 



Так как незначимым оказался коэффициент при квадратичном члене (b

), все

остальные коэффициенты пересчитываем с использованием метода наименьших

квадратов. Для этого используем упрощенную систему нормальных уравнений для k=2:

















bbbyx

bbby

22110

1248

4128

8813

Второе уравнение и столбец с коэффициентами b

исключаются из системы, т.к.

исключены коэффициенты b

и столбец матрицы

Тогда система уравнений примет вид:

















bbyx

bby

220

355128

5.467813

Откуда

494.9;2.30

220

 bb

Тогда уравнение регрессии примет вид:

221

494.933.8763.72.30 xxxy 



Адекватность полученной модели проверяем с помощью f-критерия:

 





ад



где

ад



- дисперсия адекватности;

 





=2.325 – дисперсия выходного параметра.

Дисперсию адекватности определяем по выражению

ад







где число степеней свободы

5)15(413)1('

 nkNf

; где k’=4 – число

значимых коэффициентов модели; N=13 – общее число опытов, n

=6 – число опытов в

центре плана.

 







yyS



- сумма квадратов отклонений экспериментальных значений

параметра



от среднеарифметического



по результатам 5-ти опытов в центре

плана (см. раздел 1).

         

3.92.305.302.305.292.30322.30282.3031

222























yyS



– сумма квадратов отклонений расчетных





значений функции

отклика от экспериментальных



во всех точках плана. Для расчета

составим

вспомогательную таблицу 10.

Таблица 10

№

оп.

221

494.933.8763.72.30 xxxy



























7876.55494.933.8763.72.30







55.5 0.0827

2606.40494.933.8763.72.30







39.5 0.5786

1269.39494.933.8763.72.30







39 0.0161

5999.23494.933.8763.72.30







24 0.1601

1776.41000414.1*763.72.30







41 0.0315

2224.19000414.1*763.72.30







19 0.0495

9666.602*494.9414.1*33.802.30







61.5 0.2845

4084.372*494.9414.1*33.802.30







37 0.1668

2.300002.30







31 0.64

2.300002.30







28 4.84

2.300002.30







32 3.24

2.300002.30







29.5 0.49

2.300002.30







30.5 0.09

67.10

Тогда

2739.0

3.967.10







ад



Расчетное значение F – критерия:

 

1015.0

325.2

2739.0







ад

Табличное значение F

– критерия при 5%-ном уровне значимости и числе степеней

свободы для большей дисперсии (

 



)

4151

nf

, и для меньшей дисперсии

 

5)15(413)1('

 nkNf

ад



равно F

=5.2. Так как

< F

, полученная модель

адекватна.

Раскодируем уравнение регрессии для



через формулу перехода:

;

ЭЭ













;

где x

и x

– кодированные значения факторов. Э

- натуральные значения факторов

основного уровня.

Э

f

- интервалы варьирования факторов. Э и f – натуральные

переменные значения факторов. После подстановки значений

Э

f

имеем:

;









Подставим формулы перехода x

и x

в уравнение регрессии:

0196.00906.2553.1312.68

494.9

33.8

763.72.30 ffЭ

ffЭ

y 



























Пр

авильность раскодирования проверяем путем подстановки натуральных значений

факторов в полученное уравнение. Например опыт №1: x

=+1; Э

=15 мДж; x

=+1; f

=85кГц;



=55.5 %

%5.55516.5585*0196.085*0906.215*553.1312.68





Раскодирование верно.

3. Графоаналитический метод двумерных совмещенных сечений

В результате рототабельного планирования второго порядка были получены

адекватные математические модели зависимости двух выходных параметров:

производительности процесса Q=y

и относительного линейного износа электрода-

инструмента



от двух факторов: энергии импульсов тока Э (кодированное

обозначение х

) и частоты импульсов f (кодированное обозначение х

12121

15136191025 xxxxxxy



221

98830 xxxy 



(значения коэффициентов в уравнении регрессии незначительно округлены).

В соответствии с заданием необходимо найти наибольшее и наименьшее значение

производительности процесса электроэрозионной прошивки отверстий и

соответствующие им режимы обработки, при которых износ электрода инструмента

составит 53%.

На первом этапе первое уравнение y

, содержащее два квадратичных и член с

эффектом взаимодействия, приводим к канонической форме. Для этого дифференцируем

уравнение по независимым переменным х

и приравниваем частные производные к нулю:

026610





;

030619





Составим систему уравнений:









19306

10626

Вычислим определитель системы:

7446*630*26

306

626



Определитель не равен нулю, следовательно, исследуемая поверхность отклика

имеет центр. Находим координаты центра:

25.0

744

19*630*10

744

3019

610











583.0

744

10*619*26

744

196

1026











где



– частные определители.

Подставляя

в уравнение регрессии, находим значение выходного параметра

в центре:

208.18583.0*1525.0*13583.0*25.0*6583.0*1925.0*1025



Уравнение регрессии принимает канонический вид, если координатные оси х

– х

параллельно перенести в новую координатную систему с центром S с координатами

и повернуть на угол α:



8.35

1513

arctan

2211













Тогда в новой системе координат уравнение регрессии принимает стандартный

канонический вид:

222

111QQQ

XBXByyY



где х

, х

– значение координат в новой системе после переноса и поворота старой

системы координат;

– новые коэффициенты в каноническом уравнении и

определяются из характеристического уравнения:

  

0186286*

*6*

1513

156*

2221

1211









BBBB

Bbb

bBb

Решая квадратное уравнение находим: В

=17.162, В

=10.838.

Правильность вычисления коэффициентов проверяем сравнением сумм

коэффициентов в исходном и каноническом уравнениях:

22112211

BBbb 

;

838.10162.171513 

;

2828 

Вычисление верно.

Тогда уравнение регрессии в канонической форме имеет вид:

838.10162.17208.18 XXyY



Так как

одного знака и больше нуля, то поверхность отклика представляет

собой эллиптический параболоид с вершиной в точке S, являющейся минимумом функции

и имеющим координаты:

25.0



;

583.0



Второе уравнение регрессии

221

98830 xxxy 



, содержащее только один

квадратный член, к канонической форме не приводим из-за его простоты.

На рисунке показано двумерное факторное пространство исследуемых зависимостей



в кодированных х

– х

и натуральных Э – f координатах. Показан центр S

геометрической фигуры, являющейся эллиптическим параболоидом и новые

координатные оси

XX 

после переноса в центр S и поворота на угол α=-35.8

исходной

системы координат х

– х

Все величины, показанные на графике выполнены в одном

масштабе: кодированная единица равна 25 мм. Тогда координаты центра S определяем из

пропорции:

мм

342.0

251



25.625.0*2525



мм

Соответственно,

575.14583.0*2525



мм

По условию задания необходимо определить максимальную и минимальную

производительность процесса и соответствующие им режимы обработки, при которых

износ электрода-инструмента составляет



=33%.

Подставляя это значение в уравнение регрессии



, геометрическим образом

которой является возрастающее вдоль оси х

параболическое понижение, получаем линию

равного отклика

221

9883033 xxxy 



. Уравнение приводим к уравнению параболы:

375.0125.1

 xxx

Таким образом, сечение поверхности отклика функции



плоскостью



=33% есть

парабола с осью параллельной оси х

и ветвями, направленными в сторону

отрицательного направления оси х

, т.е. влево, т.к. коэффициент при квадратичном

члене отрицателен (-1.125).

f , к Г ц

Э , м Д ж

1 51 05

8 5

6 3

4 1

+1 + 2

- 1- 2

- 2

- 1

+ 1

Построим на графике отрезок параболы, пересекающий факторное пространство.

Для этого находим точки пересечения параболы с вертикальными линиями факторного

пространства: х

= +1; 0; -1.

375.0125.11

 xxx

;

0675.0125.1

 xx

откуда

ixix 598.0444.0';598.0444.0'







Действительных корней уравнение не имеет, значит, точек пересечения параболы с

вертикальной линией

x

нет. Координаты вершины параболы равны:

444.0';597.0'





 xx

Значение координат в мм:

ммxx

мм

925.14597.0*2525







 

ммxx

мм

1.11444.0*2525







После отложения координат получим первую точку параболы – А

375.0125.10

 xxx

;

0375.0125.1

 xx

откуда

284.0';173.1'





 xx

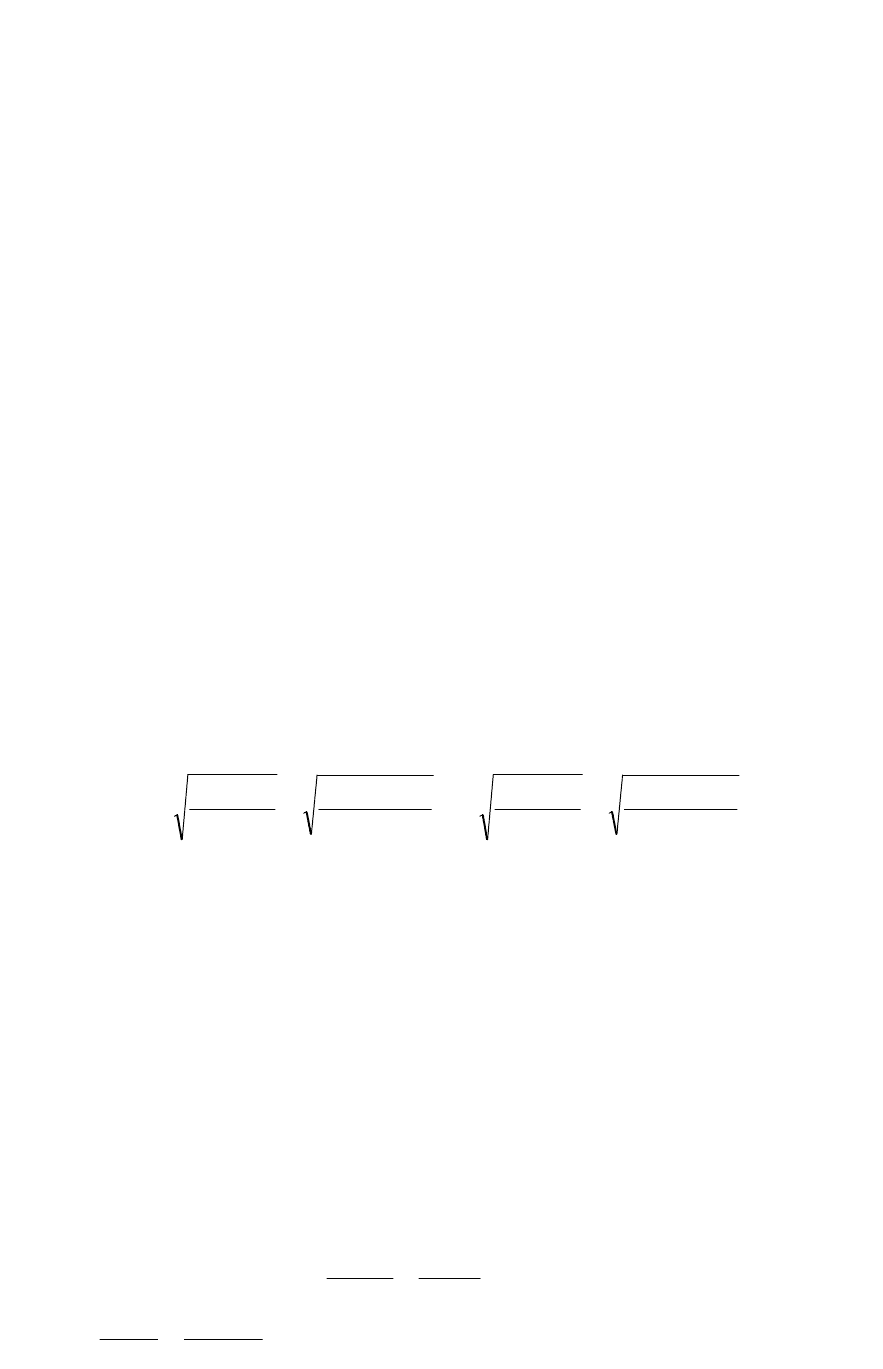
Здесь только точка

284.0'





принадлежит факторному пространству. Значение

координаты в мм:

ммxx

мм

1.7284.0*2525







На графике получили вторую точку параболы – А

375.0125.11

 xxx

;

0375.1125.1

 xx

откуда

747.0';636.1'





 xx

Здесь только точка

747.0'





находится в факторном пространстве. Значение

координаты в мм:

ммxx

мм

675.18747.0*2525







Получили третью точку параболы – А

4) Также в факторном пространстве есть четвертая точка, в которой парабола

пересекает горизонтальную линию

x

. Тогда координаты точки пересечения равны

1';25.0'





 xx

Значение координат в мм:

ммxx

мм

25.625.0*2525







 

ммxx

мм

251*2525







На графике получили четвертую точку параболы – А

Через точки А

, А

проводим плавную кривую, представляющую собой отрезок

параболы и являющийся сечением поверхности отклика



=33%.

Было получено уравнение регрессии в канонической форме для параметра

838.10162.17208.18 XXyY



Так как геометрическим образом функции отклика для параметра

является

эллиптический параболоид, то линии равного отклика, полученные в сечениях

поверхности отклика плоскостями

consty



, представляют собой эллипсы. Размеры

эллипсов определяются его полуосями а и b:

838.10

208.18

;

162.17

208.18

2211

















Видно, что с увеличением

(производительности процесса) размеры эллипсов

увеличиваются. Наибольшей производительности

max

при соблюдении требования по

износу



=33% соответствует случай, когда линия равного отклика функции

будет

представлена наибольшим по размеру эллипсом. Но при этом на графике совмещенных

двумерных сечениях поверхностей отклика обеих параметров с общими факторами х

, должна быть хотя бы одна общая точка в факторном пространстве.

Очевидно этим требованиям удовлетворяет предельная точка А

с координатами:

./813.55)1(*1525.0*13)1(*25.0*6)1(*1925.0*1025

22max

минммy



Определяем натуральное значение режимов обработки, соответствующие

max

при



=33%, т.е. в точке А

, через формулы перехода.

Так как в точке А

=-1, то натуральное значение частоты импульсов

соответствует нижнему уровню фактора

мДжff

max



. Для энергии импульсов :

22.0











 Э

ЭЭ

Откуда

кГц

25.11

2.0

225.0

2.0









