Курсовой проект - Динамическое программирование. Динамическая задача выбора объема партий. Вариант 8.2
Подождите немного. Документ загружается.

Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
ИРКУТСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра Автоматизированных систем
Допускаю к защите
Руководитель_____________________________
_____________________________
И.О. Фамилия
ДИНАМИЧЕСКАЯ ЗАДАЧА ВЫБОРА ОБЪЕМА ПАРТИЙ
наименование темы
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к курсовому проекту по дисциплине
Теория Принятия Решения
Вариант 8.2
Выполнил студент группы АСУ 06-1 _______
шифр подпись И.О. Фамилия
Нормоконтролер _______
подпись И.О. Фамилия
Курсовой проект защищен
с оценкой ____________
Иркутск 2009г.
Содержание:
1. ПОСТАНОВКА ЗАДАЧИ.................................................................................................................................................3
2. ОБОСНОВАНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ.................................................................................................5
3. КРАТКИЕ СВЕДЕНИЯ О МЕТОДЕ РЕШЕНИЯ ЗАДАЧИ......................................................................................6
4. ПРОВЕРКА ДОСТОВЕРНОСТИ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ.....................................................................9
5. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ..............................................................................................................................15
6. ЛИСТИНГ ПРОГРАММЫ, РЕАЛИЗУЮЩИЙ АЛГОРИТМ ЗАДАЧИ..............................................................16
7. РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ............................................................................................................................20
7.1 СИСТЕМНЫЕ ТРЕБОВАНИЯ............................................................................................................................................20
7.2 ОПИСАНИЕ ВОЗМОЖНОСТЕЙ........................................................................................................................................20
7.3 ОСНОВНОЕ ОКНО ПРОГРАММЫ.....................................................................................................................................21
7.4 ГЛАВНОЕ МЕНЮ ПРОГРАММЫ......................................................................................................................................22
7.5 ИСПОЛЬЗОВАНИЕ..........................................................................................................................................................22
7.5.1 Ввод данных.........................................................................................................................................................22
7.5.2 Расчет календарной программы минимальных затрат для выпуска продукции в N-ое количество
отрезков (дней)............................................................................................................................................................23
7.5.3 Вывод на экран графика зависимости целевой функции от коэффициента затрат на хранение
продукции (S)................................................................................................................................................................23
7.5.4 Результат работы программы.........................................................................................................................24
8. РЕШЕНИЕ ЗАДАЧИ КУРСОВОЙ РАБОТЫ НА ПЭВМ ПО ИСХОДНЫМ ДАННЫМ
ИНДИВИДУАЛЬНОГО ВАРИАНТА..............................................................................................................................26
9. Список использованной литературы................................................................................................................................28
2
1. Постановка задачи
Предприятие должно разработать календарную программу выпуска
некоторого вида изделий на плановый период, состоящий из N отрезков.
Предполагается, что для каждого из отрезков известен точный прогноз спроса на
выпускаемую продукцию; для разных отрезков времени спрос
))1(1( Nid
i
не
одинаков. Временем изготовления партий изделий пренебрегаем. Стоимость
выпуска партии
)(
i
xc
зависит от ее объема. Сюда же входят затраты на наладку
оборудования, которые не зависят от объёма выпускаемых изделий, но эти
затраты присутствуют в каждом изготовлении партии изделий.
Предприятию может быть выгодно изготавливать в течение некоторого
отрезка продукцию в объеме, превышающем спрос в пределах этого отрезка, и
хранить излишки, используя их для удовлетворения спроса в последующие
периоды. Вместе с тем, хранение запасов связано с определенными затратами, в
состав которых входят, в частности, расходы по содержанию запасов, арендная
плата за складские помещения и т.д. Обозначим через
)(
i
yS
затраты по
хранению избыточного запаса
i
y
на i-ом отрезке.
Требуется определить такую программу выпуска
i
x
в каждом из отрезков,
при которой минимизируется общая сумма затрат на производство и содержание
запасов, при условии полного и своевременного удовлетворения спроса на
продукцию в каждом из отрезков.
Число отрезков N= 8, сумма затрат на производство и содержание запасов
продукции на i-ом отрезке планового периода определяется выражением
,)()(),(
iiii
ySxcyxf
где
,0 если ,0
,0если ),(
)(
i
ii
i
x
xxba
xC
ii
yyS 2)(
,
8)1(1i
.
Здесь
16a
затраты на наладку оборудования в начале производства каждой
партии изделий;
ii
xxb 4)(
затраты на изготовление одного изделия.
Спрос по периодам равен соответственно
.25 ;20;30 ;12 ;25 ;8 ;15 ;10
87654321
dddddddd
Выяснить, при каком соотношении между фиксированной стоимостью
заказа партии А и удельными затратами на хранение S оптимальная программа
изготовления деталей будет совпадать со спросом, т.е.
. ...... ; ; ;
88232211
dxdxdxdx
Разработанный программный продукт должен обрабатывать числовые
значения из заданного диапазона:
а) число отрезков N может быть 7, или 8, или 9;
б) спрос на каждом отрезке планового периода может быть задан
355
i
d
);)1(1( Ni
в) затраты на наладку оборудования в начале производства каждой партии
изделий могут быть
1913 a
;
3

г) затраты на изготовление одного изделия могут быть
iii
xxbx 15)(4
;
д) затраты по хранению запаса
i
y
на i-ом отрезке могут вычисляться по формуле
ii
yyS )(
, или по формуле
ii
yyS 2)(
, или по формуле
ii
yyS 3)(
.
2. Обоснование математической модели
Cумма затрат на производство и содержание запасов продукции на i-ом
отрезке планового периода определяется выражением
,)()(),(
iiii
ySxcyxf
где
,0 если ,0
,0если ),(
)(
i
ii
i
x
xxba
xC
ii
yyS 2)(
,
8)1(1i
.
Здесь a - затраты на наладку оборудования в начале производства каждой партии
изделий;
ii
xxb 4)(
затраты на изготовление одного изделия.
Общий вид:
4
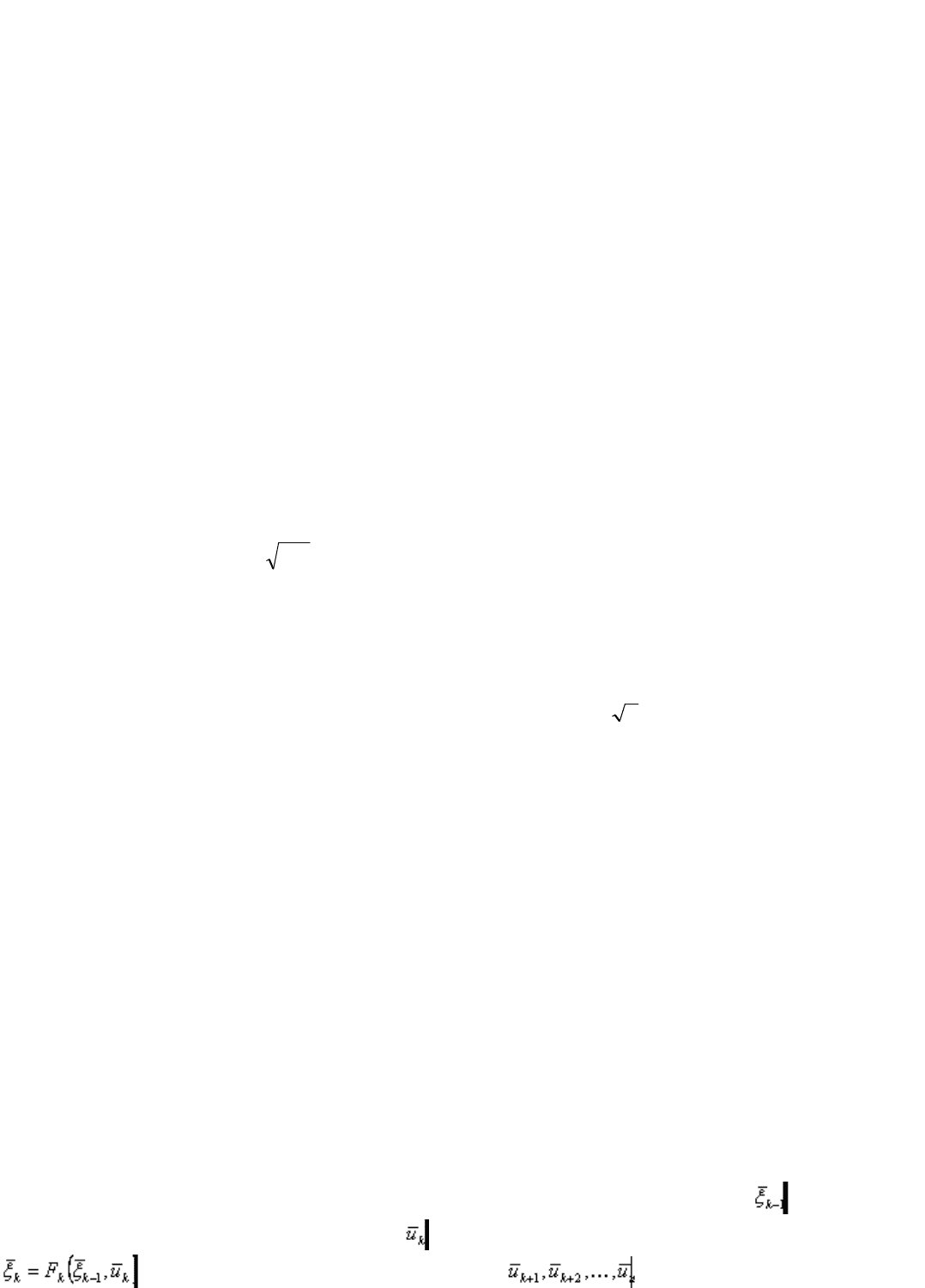
N
i
i
N
n
ii
ySxBNaxf
11
i
)()()y ,(
Где, A > 0 – стоимость одного запуска станка,
N > 0– количество запусков станка.
B > 0– стоимость изготовления одной детали.
S > 0– стоимость хранения одной детали.
i
x
- количество деталей, произведенных в i-ый день.
i
y
- количество деталей, взятых со склада в i-ый день.
niyx
ii
)1(1,0,
- производство, и поставка деталей не может быть
отрицательной.
iiii
dyxy
1
система ограничений, где
i
x
- количество деталей производимых
в i-ый день,
i
y
- количество деталей получаемых со склада в i-ый день,
1i
y
-
количество деталей сданных на склад в (i-1)-ый день, причем y для первого и
последнего дня равен нулю, так как нет смысла сдавать детали на склад в
последний день и невозможно получить со склада детали в первый день, так как
склад пока пуст. (y
1
=0 и у
n
=0),
i
d
- спрос на продукцию в i-ый день.
Математическая модель:
N
i
i
N
n
ii
yxNxf
11
i
2)416()y ,(
niyx
yx
yxyyxyyxyyxyyxyyxyxy
ii
)1(1,0,
10
,15,8,25,12,30,20,25
11
22133244355466577687
)416( N
- Один запуск станка стоит 16 условных единиц, а производство одной
детали 4. Хранение одной детали за одни сутки составляет
2
условных единиц.
3. Краткие сведения о методе решения задачи
Метод динамического программирования состоит в том что оптимальное
управление строится постепенно. На каждом шаге оптимизируется управление
только этого шага. Вместе с тем на каждом шаге управление выбирается с учётом
последствий, так как управление, оптимизирующее целевую функцию только для
данного шага, может привести к неоптимальному эффекту всего процесса.
Управление на каждом шаге должно быть оптимальнымZ с точки зрения процесса
в целом. Это основное правило динамического программирования,
сформулированное Беллманом, называется принципом оптимальности.
Итак, каково бы не было начальное состояние системы перед очередным
шагом, управления на этом этапе выбирается так, чтобы выигрыш на данном шаге
плюс оптимальный выигрыш на всех последующих шагах был оптимальным.
Так, если система в начале k - шага находится в состоянии Zи мы
выбираем произвольное управление , то она придет в новое состояние в
(1), и последующие управления должны выбираться
5
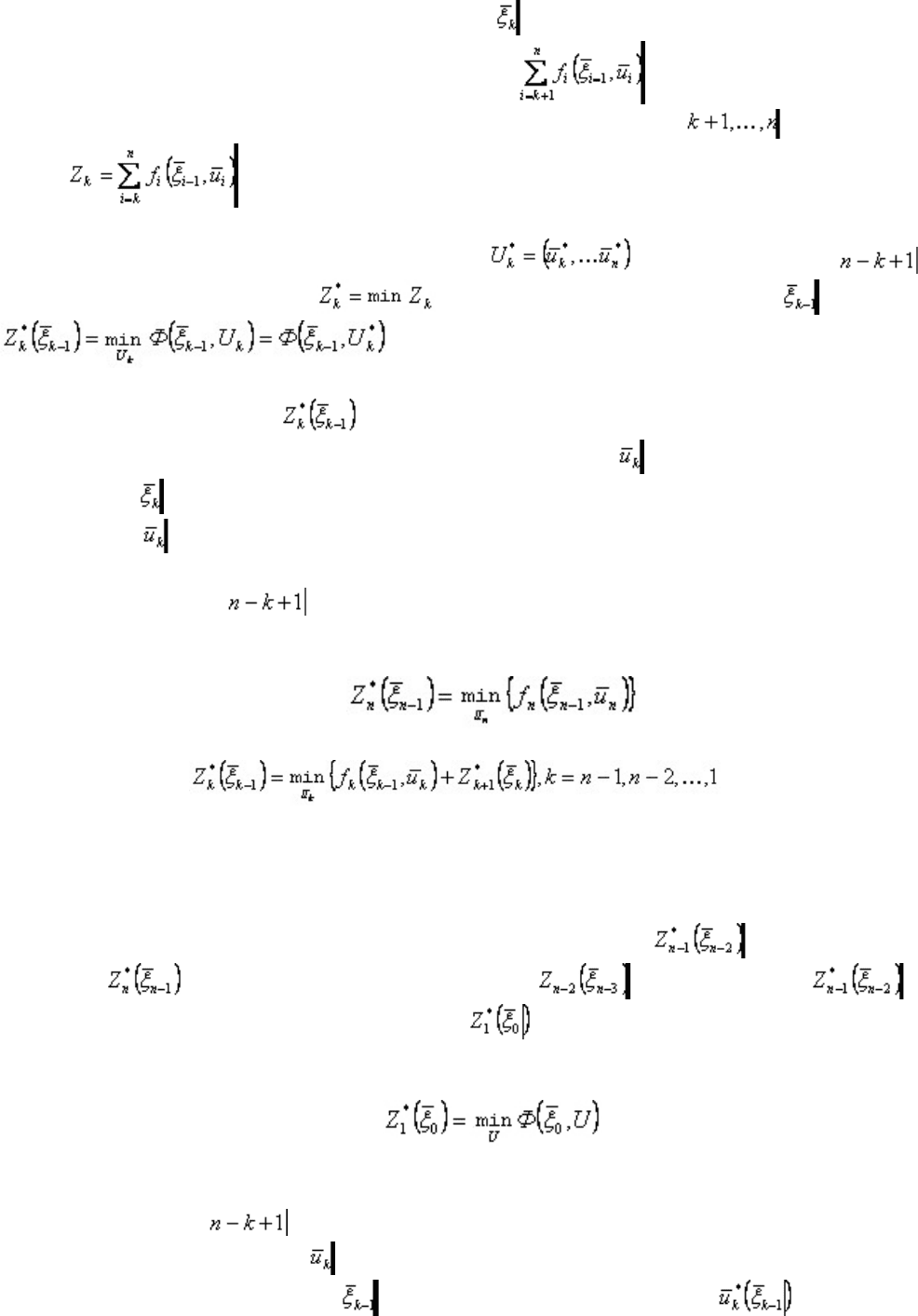
оптимальными относительно состояния . Последнее, означает, что этих
управлениях минимизируетсяZ величина , то есть показатель
эффективности на последующих до конца процесса шагах . Обозначим
через .
Выбрав оптимальное управление Zна оставшихся Z
шагах, получим величину , которая зависит только от , то есть
.
Назовем величину Zусловным минимумом. Если мы теперь выберем
на k-м шаге некоторое произвольное управление , то система придет в
состояние . Согласно принципу оптимальности, необходимо выбирать
управление так, чтобы оно в совокупности с оптимальным управлением на
последующих шагах (начиная с (k+1)-го) приводило бы к общему показателю
эффективности наZ Zшагах, начиная с k-го и до конца. Это положение в
аналитической форме можно записать в виде следующего соотношения:
,
Z,ZZ ZZZ(2)
получившего название основного функционального уравнения динамического
программирования, или основного рекуррентного уравнения Беллмана.
Из уравнения (2) может быть получена функция , если известно
функция . Аналогично можно получить , если известно Zи
т. д., пока не будет определена величина , представляющая по определению
значение показателя эффективности процесса в целом:
.
Решая уравнение (2) для определения условного максимума показателя
эффективности за Zшагов, начиная с k-го, мы определяем соответствующее
оптимальное управление , при котором этот максимум достигается. Это
управление также зависит от ; будем обозначать его через Zи называть
условным оптимальным управлением на k-м шаге. Основное значение уравнения
(2), в котором реализована идея динамического программирования, заключается в
том, что решение исходной задачи определения максимума функции
6

Zn переменных Zсводится к решению последовательности
n задач, задаваемых соотношениями (1), каждое из которых является задачей
максимизации функции одной переменной .
В результате последовательного решения п частных задач на условный
максимум определяют две последовательности функций: Z- условные
минимумы и соответствующие им Z- условные оптимальные управления.
Указанные последовательности функций в дискретных задачах получают в
табличной форме, а в непрерывных моделях - аналитически. После выполнения
первого этапа (условной оптимизациии) приступают ко второму этапу -
безусловной оптимизации.
Если начальное состояние Zзадано , то непосредственно
определяют минимум целевой функции
,
а затем - искомое безусловное оптимальное управление по цепочке
.ZZZZZZZZZZZZZZZZZ (3)
Если задано множество начальных состояний , то дополнительно решают
еще одну задачу на минимум
,
откуда находят , а затем по цепочке (3) - безусловное оптимальное управление.
В рассмотренных рекуррентных соотношениях предписывают начинать
вычисления с последнего этапа и затем передвигаться назад до этапа 1. Такой
метод вычислений известен как алгоритм обратной прогонки. Если расчеты
осуществляются в естественном порядке следования этапов, то такой метод
вычислений известен как алгоритм прямой прогонки.
Приведем рекуррентные соотношения для этого случая. Уравнения со-
стояний для прямого хода удобно записывать в виде
.
Введем в рассмотрение условные минимумы показателя эффективности за k
шагов, от 1-го до k-го включительно, - величину . Повторив приведенные
рассуждения, придем к следующей системе уравнений Беллмана:
7
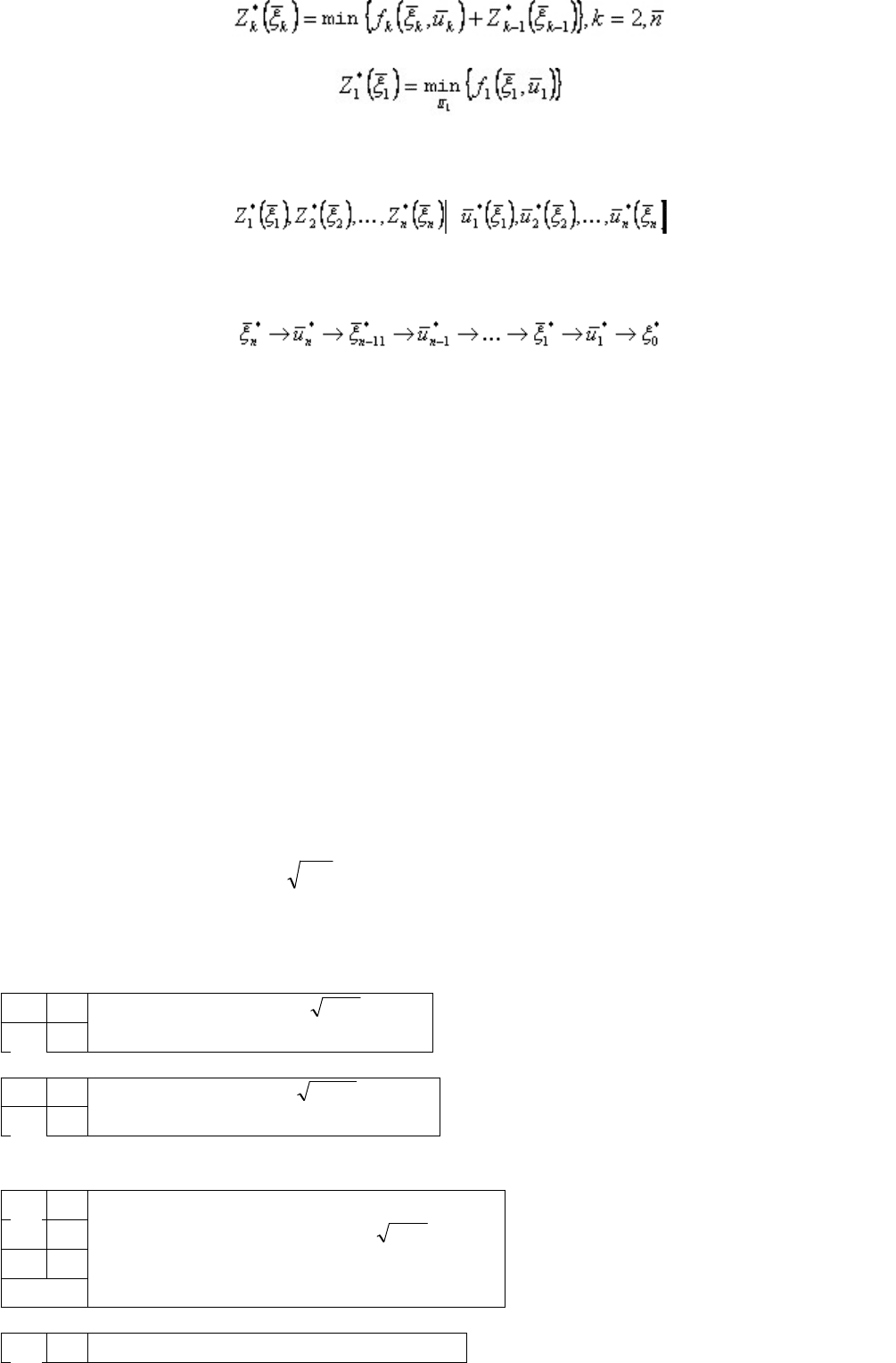
;
.
В результате решения этих уравнений получим последовательности
; .
Далее определим безусловное оптимальное управление по цепочке
.
4. Проверка достоверности полученных результатов
N
i
i
N
n
ii
yxNxf
11
i
2)416()y ,(
0,
8,15,10
1122132
ii
yx
yxyxyxy
1.
10
32
xy
3
x
10
560*2)10*416()y ,(
i
i
xf
2
y
0
3
x
0
47,410*2)0*40()y ,(
i
i
xf
2
y
10
2.
15
221
yxy
3
x
10
1320*2))1510(42*16()y ,(
i
i
xf
2
y
0
2
x
15
1
y
0
3
x
10
8
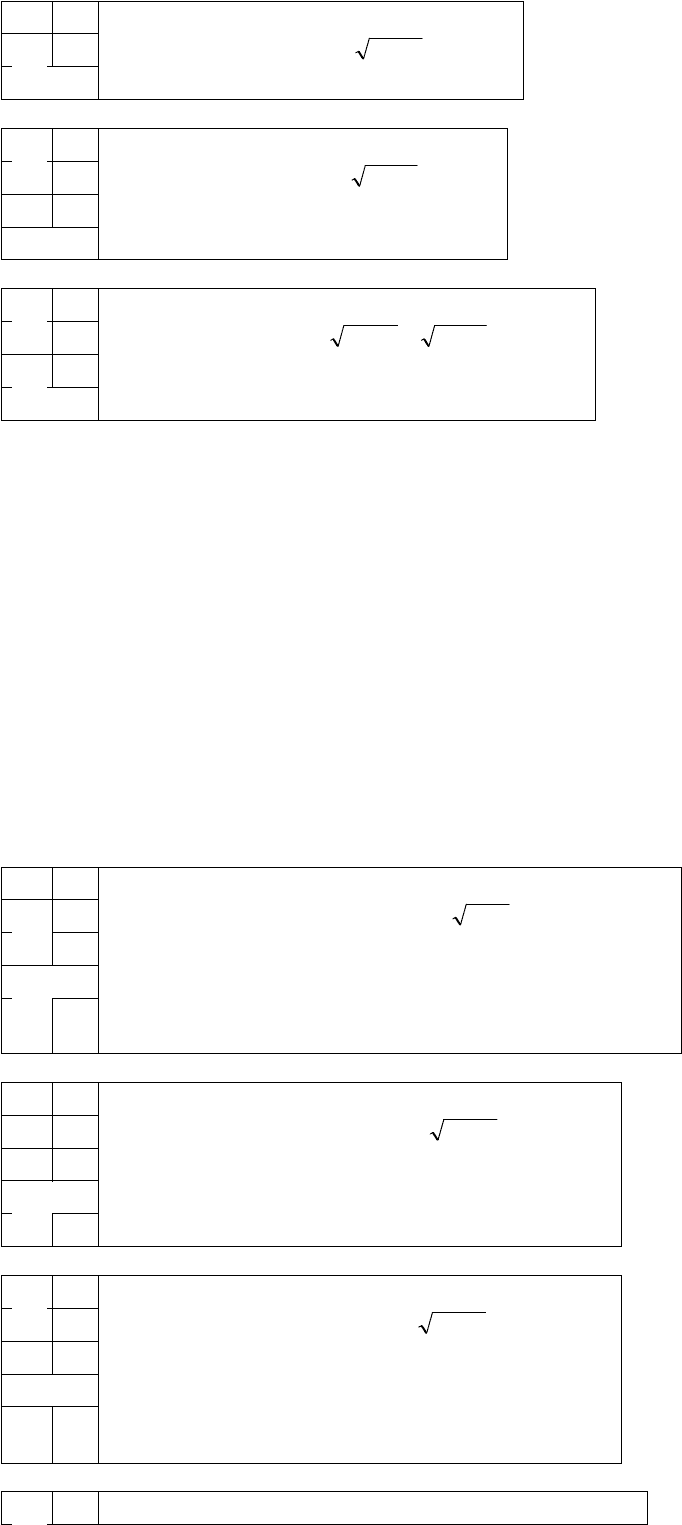
47,6115*2)10*416()y ,(
i
i
xf
2
y
0
2
x
0
1
y
15
3
x
0
11610*2)25*416()y ,(
i
i
xf
2
y
10
2
x
25
1
y
0
3
x
0
54,1110*225*2)0*40()y ,(
i
i
xf
2
y
10
2
x
0
1
y
25
3.
8
11
yx
3
x
10
1800*2))81510(43*16()y ,(
i
i
xf
2
y
0
2
x
15
1
y
0
1
x
8
3
x
10
48,16915*2))1023(42*16()y ,(
i
i
xf
2
y
0
2
x
0
1
y
15
1
x
23
3
x
0
47,16810*2))825(42*16()y ,(
i
i
xf
2
y
10
2
x
25
1
y
0
1
x
8
3
x
0
9
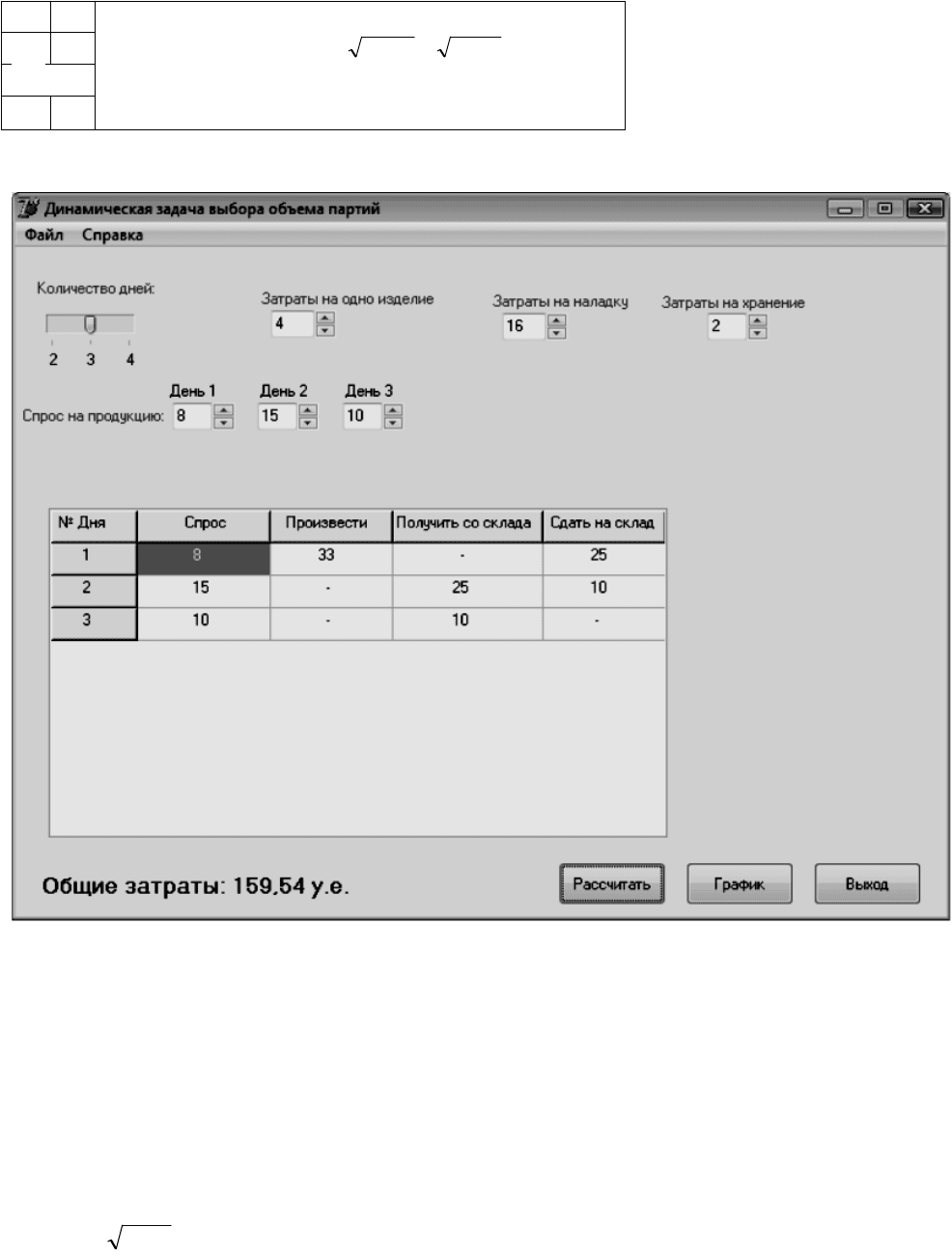
54,159)10*225*2()33*416()y ,(
i
i
xf
2
y
10
2
x
0
1
y
25
1
x
33
Рассчитав 3 шага, можно проверить программу, убрав ее ограничения на
количество отрезков N. Подставим значения в программу:
Получаем, что расхождений с программой нет, следовательно, результаты
достоверны.
Теперь проверим правильность вычисления соотношения между
фиксированной стоимостью заказа партии А и удельными затратами на хранение
S, при которой, оптимальная программа изготовления деталей будет совпадать со
спросом, т.е.
. ...... ; ; ;
332211 nn
dxdxdxdx
На графике, приведенном ниже, видно, что при затратах на хранение (S)
равных
i
y26
, целевая функция уже не зависит от S.
10
