Курсова робота - Методи розв’язування одновимірних та багатовимірних нелінійних оптимізаційних задач та задач лінійного цілочислового програмування

Подождите немного. Документ загружается.

000

)1(

4)(































xf

Знайдемо похідну цієї функції по



і прирівняємо її до нуля:

185

106

)(

)1(







, отже покладаємо



=1, таким чином





























5/9

5/14

5/9

5/14

)1(



. Знайдемо значення цільової функції в цій точці і

перевіримо умови зупинки:

68,12

317

4)(

)1(





























xf

1,068,12068,12)()(

)0()1(

 xfxf

Отже знаходимо нове наближення оптимального плану вихідної задачі

аналогічним чином. Покладаємо, що

1kk

. Градієнт цільової функції в

точці

 

5/9,5/14

)1(

x

буде рівним:

 

   

2,1,3

22,

4(5/9,5/14

)1(

 fxf

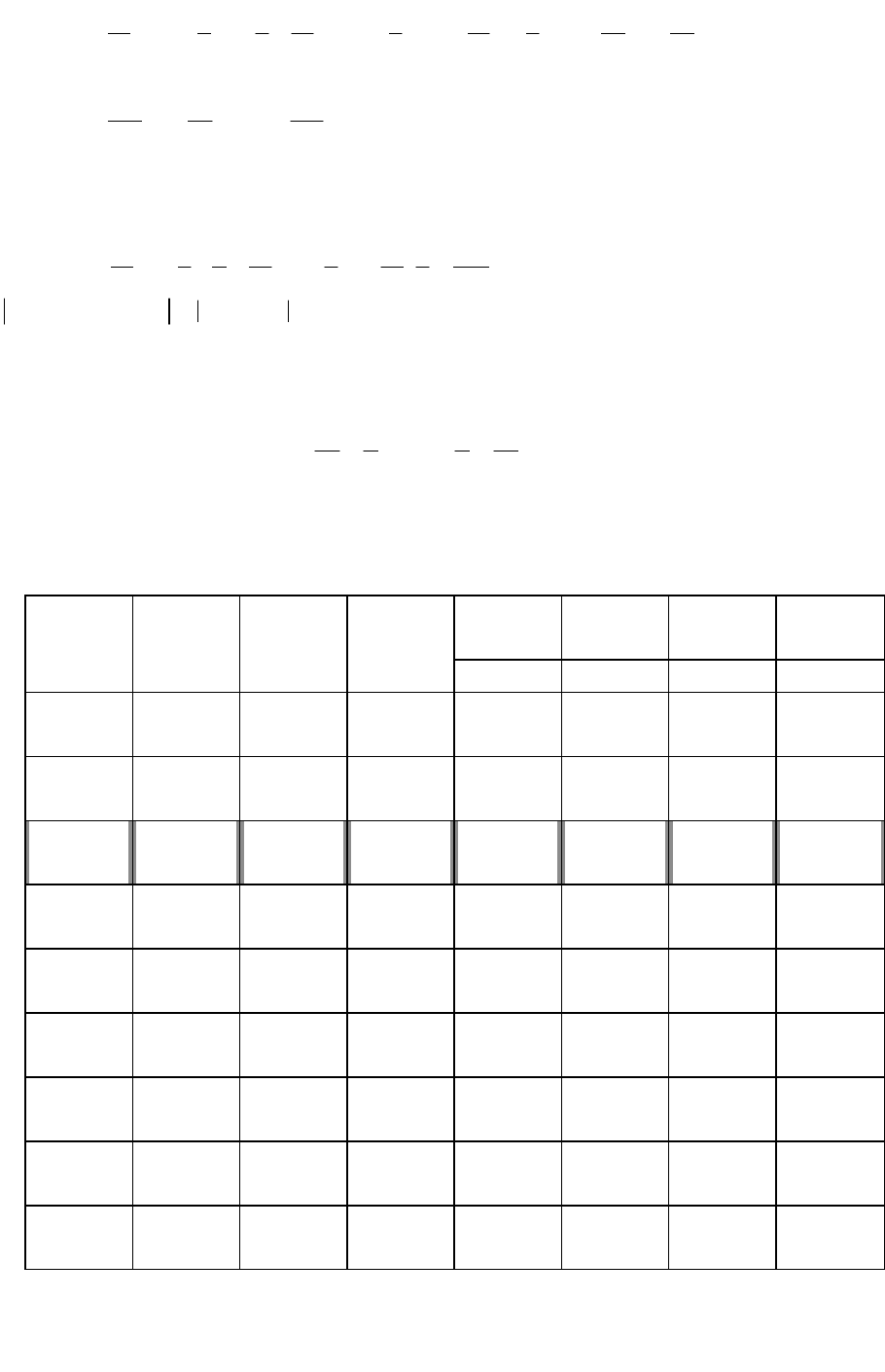
Знаходимо за допомогою симплекс-методу максимум функції



















2173

max2,13

2,1

xxF

і Базис С

3 6/5 0 0

1 А

0 21 3 7 1 0

2 А

0 1 1 -1 0 1

3 0 - 3 -6/5 0 0

1 А

0 18 0 10 1 -3

2 А

3 1 1 -1 0 1

3 3 0 -21/5 0 3

1 А

6/5 9/5 0 1 1/10 -3/10

2 А

3 14/5 1 0 1/10 7/10

3 264/5 0 0 21/50 87/50

Позначимо через

)1(

оптимальний розв’язок даної задачі. Отже

)5/9,5/14(

)1(

F

. Визначимо тепер

)2(

 

)1(1

)1()2(

xFxx 







































































5/9

5/14

5/9

5/14

5/9

5/14

5/9

5/14

)2(



68,12)(

)2(

xf

1,0068,1268,12)()(

)1()2(

 xfxf

. Тобто критерій зупинки виконано. Отже

 

5/9,5/14

)2(

x

являється оптимальним розв’язком вихідної задачі, тобто

 

8,12,5/9,5/14

max

)2(*

 zxx

b. метод штрафних функцій

Цей метод відноситься до групи непрямих методів розв’язання задач

нелінійного програмування виду:

 

опукліgixxxfфункціїдеnjx

mibxxxg

xxxfz

inj

ini







),...,,(,,10

,1,,...,,

min),...,,(

Він зводить задачу з обмеженнями в послідовність задач безумовної

оптимізації деяких допоміжних функції. Останні отримуються шляхом

модифікації цільової функції за допомогою функій-обмежень таким чином,

щоб обмеження в явному вигляді в задачі оптимізації не фігурували. Це

забезпечує можливість застосування методів безумовної оптимізації. В

загальному випадку допоміжна функція має вигляд:

   

xxxHxxxfF ,...,,,...,,

2121



, де функція

 

xxxH ,...,,

визначається з

обмежень вихідної задачі і називається штрафною функцією. Необхідно, щоб

при порушенні обмеження вона “штрафувала” функцію Z, тобто збільшувала

її значення. В такому випадку Z буде знаходитися всередині області

обмежень. Штрафну функцію можна будувати різними способами.

Розглянемо один з варіантів, коли

     

nin

xxxgxxxaxxxH ,...,,,...,,,...,,

2121





, де

 

















0,...,,,

0,...,,,0

,...,,

niii

nii

xxxgbякщоL

xxxgbякщо

xxxa

- параметр штрафної

функції.

Далі розв’язують задачу мінімізації для функції

, використовуючи

один з відомих методів безумовної оптимізації. Будемо розв’язувати задачу

мінімізації для

градієнтним методом зі сталим кроком. Тоді алгоритм

розв’язування задачі буде таким:

1. Обирається точність обчислень, а в якості початкової точки

(0)

беруть довільну точку, яка належить допустимій множині

задачі. Також зазначається крок



і покладають

0k 

2. Знаходять

( )

( 1) ( ) ( )

( )

max 0, ( )

j n

k k k

j j i

j j

g x

f x

x x a x

x x









 



  

 

 

 



. Якщо

точка

( )k

належить допустимій множині задачі, то коефіцієнти

( )

a x

будуть рівними нулю, якщо ж не належать, то вибираємо

параметри

так, щоб точка

( 1)k



належала допустимій

множині.

3. Перевіряють чи виконується умова







)()(

)()1( kk

xfxf

. Якщо

не виконується, то переходять до наступного кроку, якщо

виконується , то

* ( 1) * ( 1)

( ) ( ),

k k

f x f x x x

 

 

4. Покладають, що

1k k 

і переходять до кроку 2.

Перейдемо тепер безпосередньо до нашої задачі. Так як ми

розглянули алгоритм методу штрафних функцій для випадку пошуку

мінімуму функції, то перейдемо від задачі максимізації до задачі мінімізації:

2 2

1 2 1 2 1 2

1 2

1,2

4 2 min

3 7 21

x x x x x x

x x



     



 



 









Запишемо штрафну функцію:

2 2

1 2 1 2 1 2

4 2

f x x x x x x    

і розв’яжемо

тепер задачу мінімізації для цієї функції.

2 2

1 2 1 2 1 2

1 1 2

4 2

3 7

f x x x x x x

g x x

    

 

 

За точність обчислень оберемо

0,1





, а крок

0,1





, а початкову

точку візьмемо таку ж як ми брали у методі Франка-Вулфа, тобто

)0;0(

)0(

x

Отже

1,2

( ) ( )

( )

( 1) ( ) ( ) ( )

1 2

( ) ( )( )

max 0, 0,1 ( ) ( )

j j

k k

k k k k

j j

j j j

g x g xf x

x x a x a x

x x x

 



 

 

   

 

  

 

 

( 1) ( ) ( ) ( ) ( ) ( )

1 1 1 2 1 2

max 0, 0,1 4 3 ( ) ( )

k k k k k k

x x x x a x a x



      

;

 

( 1) ( ) ( ) ( ) ( ) ( )

2 2 2 1 1 2

max 0, 0,1 2 2 7 ( ) ( )

k k k k k k

x x x x a x a x



      

Тобто

 

(1)

max 0,0 0,1 4 0 0 0 0 0,4x        

 

(1)

max 0,0 0,1 2 2 0 0 0 0x        

Точка

 

(1) (1) (1)

1 2

, 0,4, 0,2x x x 

належить допустимій множині задачі, оскільки

задовольняє обмеженням задачі:

3 0,4 7 0,2 21

0,4 0,2 1

0,4 0

0,2 0

   





 













Обчислимо значення штрафної функції в цій точці:

(1) 2 2

( ) 4 0,4 2 0,2 0,4 0,2 0,4 0,2 1,96

f x          

. Перевіримо критерій

зупинки:

(1) (0)

( ) ( ) 1,96 0 1,96 0,1f x f x     

, отже тепер по аналогії шукаємо

наступне наближення до оптимального розв’язку.

 

(2)

max 0,0,4 0,1 4 0,4 0,2 0,78x      

 

(2)

max 0,0,2 0,1 2 2 0,2 0,4 0,4x       

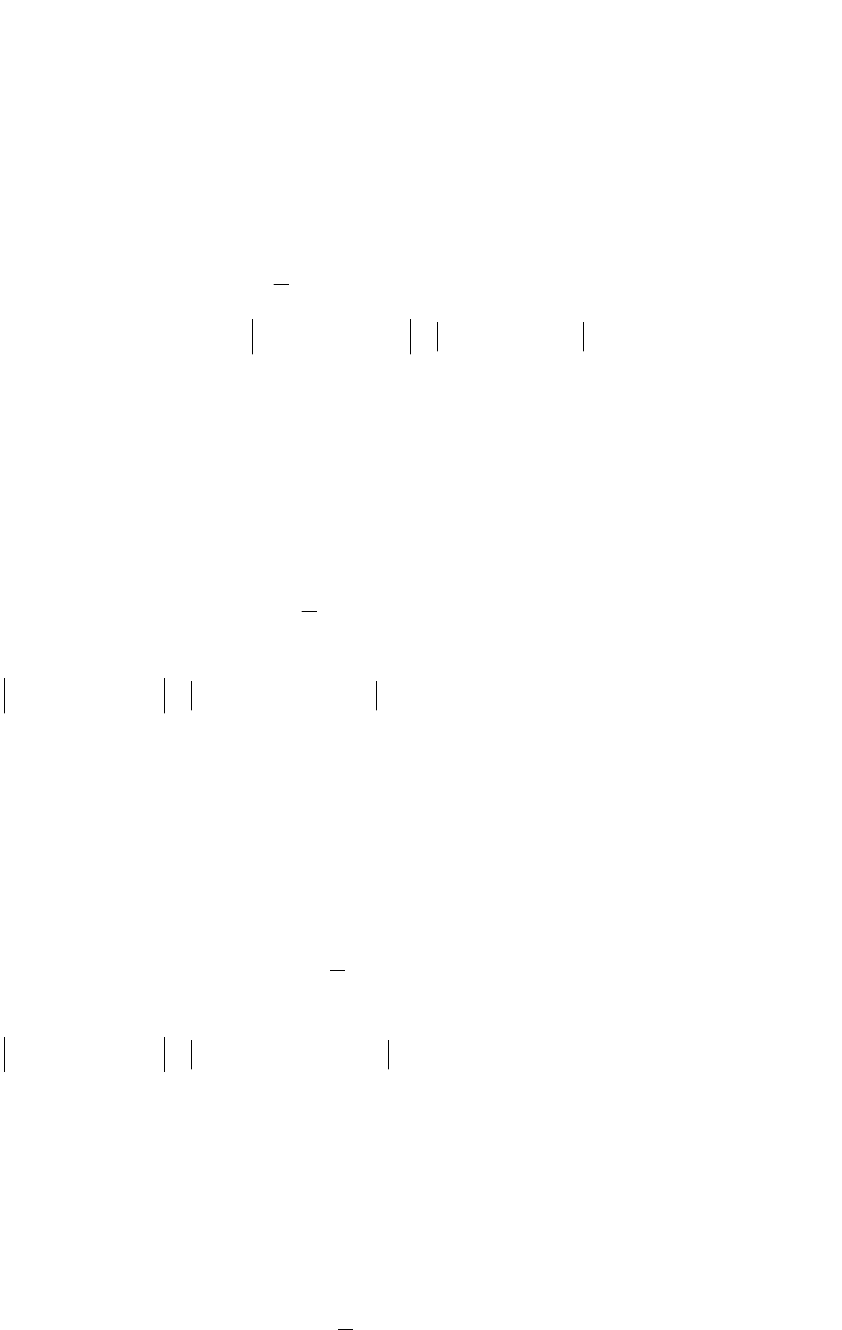
Точка

 

(2) (2) (2)

1 2

, 0,78, 0,4x x x 

належить допустимій множині задачі,

оскільки задовольняє обмеженням задачі:

3 0,78 7 0,4 21

0,78 0,4 1

0,78 0

0,4 0

   





 













Обчислимо значення штрафної функції в цій точці:

(2) 2 2

( ) 4 0,78 2 0,4 0,78 0,4 0,78 0,4 3,7678

f x          

. Тепер перевіримо

критерій зупинки:

(2) (1)

( ) ( ) 3,7678 1,96 1,8078 0,1f x f x     

, отже шукаємо

наступне наближення до оптимального розв’язку.

 

(3)

max 0,0,78 0,1 4 0,78 0,4 1,142x      

 

(3)

max 0,0,4 0,1 2 2 0,4 0,78 0,598x       

Точка

 

(3) (3) (3)

1 2

, 1,142, 0,598x x x 

належить допустимій множині задачі,

оскільки задовольняє обмеженням задачі.

Обчислимо значення штрафної функції в цій точці:

(3) 2 2

( ) 4 1,142 2 0,598 1,142 0,598 1,142 0,598 5,43723

f x          

Тепер перевіримо критерій зупинки:

(3) (2)

( ) ( ) 5,43723 3,7678 1,66943 0,1f x f x    

, отже шукаємо наступне

наближення до оптимального розв’язку.

 

(4)

max 0,1,142 0,1 4 1,142 0,598 1, 4876x      

 

(4)

max 0,0,598 0,1 2 2 0,598 1,142 0,7926x       

Точка

 

(4) (4) (4)

1 2

, 1,4876, 0,7926x x x 

належить допустимій множині задачі,

оскільки задовольняє обмеженням задачі.

Обчислимо значення штрафної функції в цій точці:

(4) 2 2

( ) 4 1,4876 2 0,7926 1,4876 0,7926 1,4876 0,7926 6,97998

f x          

Тепер перевіримо критерій зупинки:

(4) (3)

( ) ( ) 6,97998 5,43723 1,54275 0,1f x f x     

, отже шукаємо наступне

наближення до оптимального розв’язку.

 

(5)

max 0,1,4876 0,1 4 1,4876 0,7926 1,8181x      

 

(5)

max 0,0,7926 0,1 2 2 0,7926 1,4876 0,98284x       

Точка

 

(5) (5) (5)

1 2

, 1,8181, 0,98284x x x 

належить допустимій множині задачі,

оскільки задовольняє обмеженням задачі.

Обчислимо значення штрафної функції в цій точці:

(5) 2 2

( ) 4 1,8181 2 0,98284 1,8181 0,98284 1,8181 0,98284 8,40626

f x          

Тепер перевіримо критерій зупинки:

(5) (4)

( ) ( ) 8,40626 6,97998 1,42628 0,1f x f x    

, отже шукаємо наступне

наближення до оптимального розв’язку.

 

(6)

max 0,1,8181 0,1 4 1,8181 0,98284 2,761145x      

 

(6)

max 0,0,98284 0,1 2 2 0,98284 1,8181 1,168082x       

Точка

 

(6) (6) (6)

1 2

, 2,134574, 1,168082x x x 

належить допустимій множині задачі,

оскільки задовольняє обмеженням задачі.

Обчислимо значення штрафної функції в цій точці:

(6) 2 2

( ) 4 2,134574 2 1,168082 2,134574 1,168082 2,134574 1,168082 9,7252

f x          

Тепер перевіримо критерій зупинки:

(6) (5)

( ) ( ) 9,7252 8, 40626 1,31894 0,1f x f x     

, отже шукаємо наступне

наближення до оптимального розв’язку.

 

(7)

max 0,2,761145 0,1 4 2,761145 1,168082 2,437925x      

 

(7)

max 0,1,168082 0,1 2 2 1,168082 2,761145 1,347923x       

Точка

 

(7) (7) (7)

1 2

, 2,437925, 1,347923x x x 

не належить допустимій множині

задачі, оскільки не виконується друге обмеженням задачі (

2,437925 1,347923 1,09 1  

), отже параметр

( )

a x

відмінний від нуля.

Оберемо його так, щоб друге обмеження задачі виконувалося.

 

(8)

1 2 2

max 0,2,437925 0,1 4 2,437925 1,347923 2,7289248 0,1x a a       

 

(8)

2 2

max 0,1,347923 0,1 2 2 1,347923 2,437925 1,1951303 0,1x а       

З другого обмеження задачі маємо:

2 2

2,7289248 0,1 1,1951303 0,1 1

0,2 0,5337945

2,67

а а

   

 



Отже в якості параметру

візьмемо

2,68а 

. Тоді

(8)

1 2

2,7289248 0,1 2,7289248 0,1 2,68 2,461x a     

(8)

2 2

1,1951303 0,1 1,1951303 0,1 2,68 1,463x а     

Точка

 

(8)

2,461, 1, 463x 

належить допустимій множині задачі.

Обчислимо значення штрафної функції в цій точці:

(8) 2 2

( ) 4 2,461 2 1,463 2,461 1,463 2,461 1,463 11,2018

f x          

І так далі продовжується процес пошуку нового наближення до

розв’язку задачі.

Як бачимо, метод штрафних функцій сходиться значно повільніше,

ніж метод Франка-Вулфа. Це може бути пов’язано з тим, що початкове

наближення знаходиться далеко від мінімуму функції, або ж необхідно

обрати більший крок.

V. Розв’язання задачі цілочислового програмування

Розв’яжемо задачу цілочислового програмування



















)4(,0

)3(623

)2(93

)1(max4

2,1

ціліx

xxz

а) графічно:

Оскільки число невідомих задачі дорівнює двом, рішення можна

знайти, використовуючи геометричну інтерпретацію заадчі. Для цього,

насамперед, побудуємо багатокутник рішення задачі, що складає у

визначенні максимальне значення лінійної функції (1) при виконанні умов (2)

і (3) (мал. 1). Координати всіх точок побудованого багатокутника рішення

ОАВС задовольняють систему лінійних нерівностей 2-3. Разом з тим умові

(4), тобто умові цілочисельності змінних, задовольняють координати лише 20

точок, відзначених на мал. 1.

Щоб знайти точку, координати якої визначають рішення вихідної

задачі, замінимо багатокутник ОАВС багатокутником, що містить усі

припустимі точки з цілочисловими координатами і таким, що координати

кожної з вершин є цілими числами. Виходить, якщо знайти точку максимуму

функції (1) на отриманому багатокутнику, то координати цієї точки і

визначать оптимальний план задачі.

Для цього побудуємо вектор

=(4; 1) – градієнт цільової функції і

перпендикуляр до неї – лінію рівня цільової функції, тобто лінію, в точках

якої цільова функція приймає одне й те ж значення. Побудовану пряму

пересуваємо в напрямку вектора

доти, поки вона не пройде через останню

загальну точку її з даним багатокутником. Координати цієї точки і

визначають оптимальний план, а значення цільової функції в ній є

максимальним.

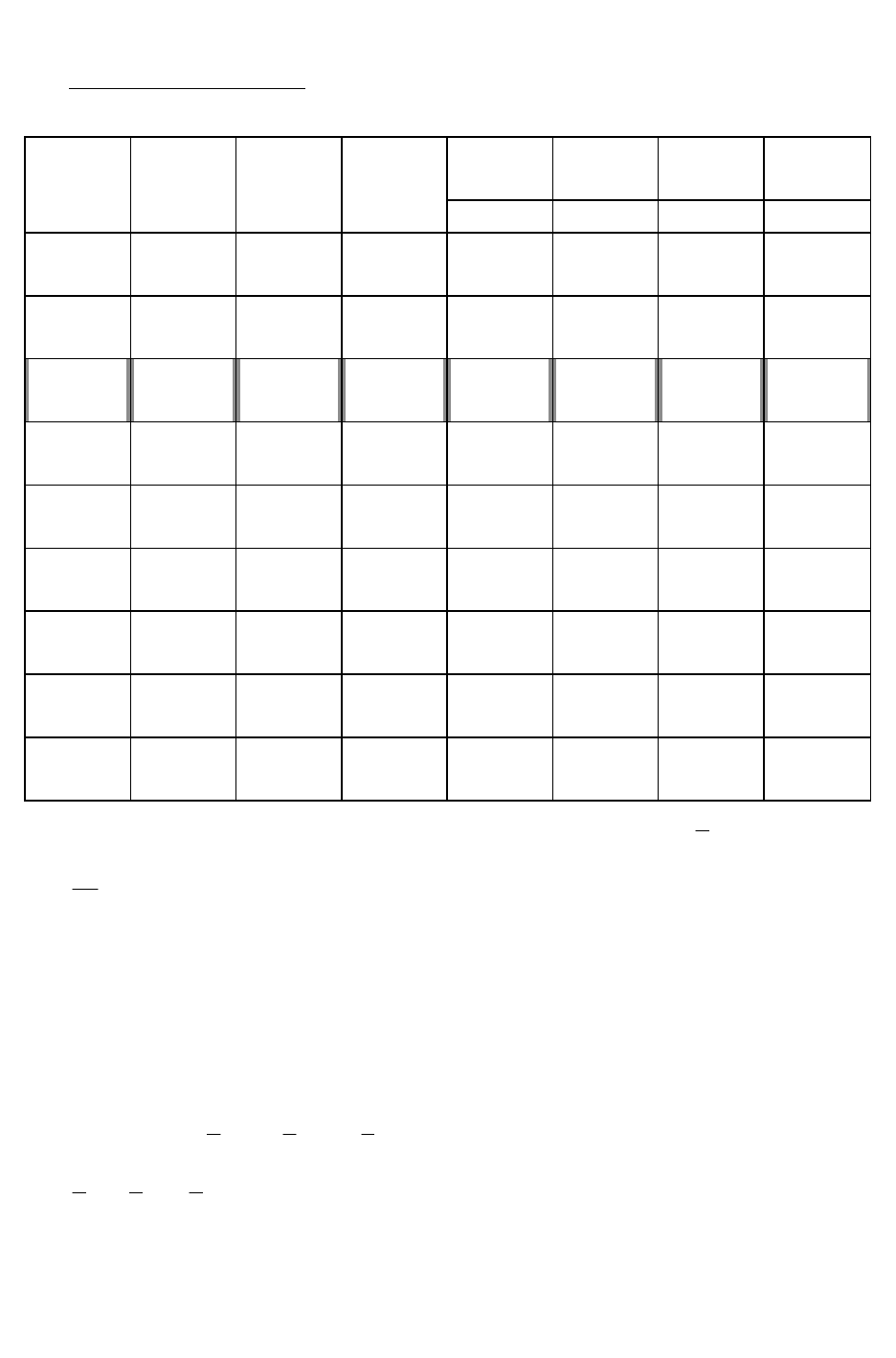
У даному випадку шуканою є точка Е(2;3), у якій цільова функція

приймає максимальне значення

11324

max

Z

. Отже, координати точки Е

визначають оптимальний план задачі 1 — 4.

б) методом Гоморі:

Для рішення задачі цілочислового програмування методом Гоморі спочатку визначимо симплекс-

методом оптимальний план задачі 1 —3 без умови цілочисельностісті змінних:

і Базис С

4 1 0 0

1 А

0 9 3 1 1 0

2 А

0 6 3 -2 0 1

3 0 - 4 -1 0 0

1 А

0 3 0 3 1 -1

2 А

4 2 1 -2/3 0 1/3

3 8 0 -11/3 0 4/3

1 А

1 1 0 1 1/3 -1/3

2 А

4 8/3 1 0 2/9 1/9

3 35/3 0 0 11/9 1/9

Тобто оптимальний план буде мати вигляд:













 1;

, при цьому

max

Z

. Отримане рішення є оптимальним для задачі лінійного

програмування, але недопустимим для задачі лінійного цілочислового

програмування, оскільки змінна

приймає дробове значення. Тому

будуємо додаткове обмеження для змінної

, яке є правильним

відтинанням, використовуючи перший алгоритм Гоморі:

   

bxa 





. Тобто

з останньої симплекс-таблиці матимемо:

   

)5(62

4321















































xxxx

Умову 5 записуємо в канонічній формі:

543

 xxx

і приєднуємо до

останньої симплекс-таблиці 3-ім рядком, при цьому рядок оцінок не зміниться. Тепер рішення задачі,

утвореної в результаті приєднання додаткового обмеження, знаходимо за допомогою двоїстого симплекс-

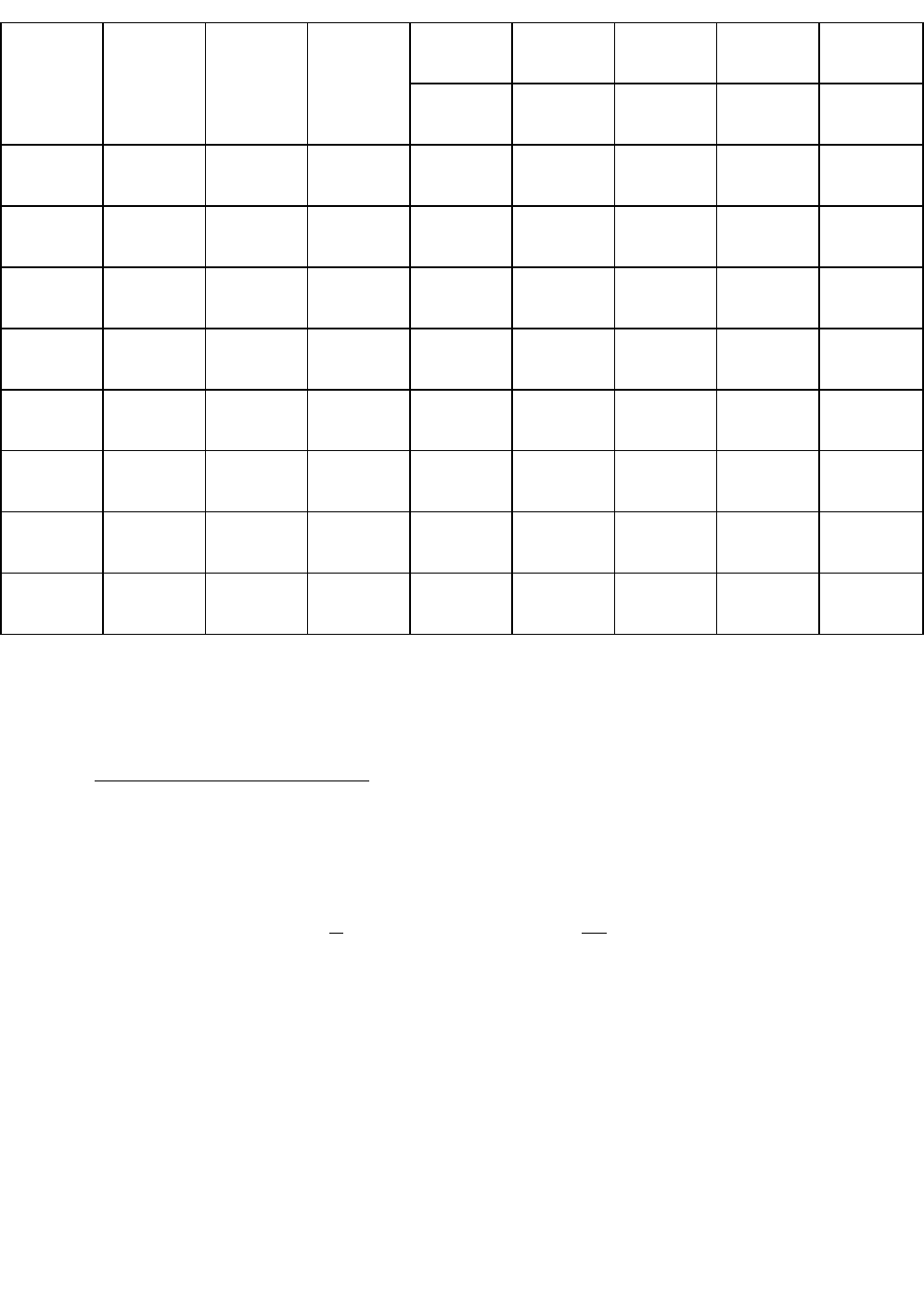
методу.

і Базис С

4 1 0 0 0

1 А

1 1 0 1 1/3 -1/3 0

2 А

4 8/3 1 0 2/9 1/9 0

3 А

0 -6 0 0 -2 -1 1

4 35/3 0 0 11/9 0 0

1 А

1 3 0 1 1 0 -1/3

2 А

4 2 1 0 0 0 1/9

3 А

0 6 0 0 2 1 -1

4 11 0 0 1 0 1/9

З останньої симплекс-таблиці видно, що вихідна задача цілочислового

програмування має оптимальний план Х* = (2; 3). При цьому плані значення

цільової функції дорівнює:

11324

max

Z

в ) методом Ленг і Дойг

Як і у випадку знаходження розв’язку задачі цілочислового

програмування за допомогою методу Гоморі, спочатку визначаємо симплекс-

методом оптимальний план задачі (1) —(3) без умови цілочисельності

змінних. З попереднього пункту маємо оптимальне для задачі лінійного

програмування (1-3):













 1;

, при цьому

max

Z

Оскільки оптимальне рішення задачі лінійного програмування 1-3 не

задовольняє умові цілочисельності, метод Ленг і Дойг заміняє простір рішень

задачі лінійного програмування так, що в кінцевому результаті отримуємо

рішення задачі цілочислового лінійного програмування. Для цього спочатку

обираємо змінну, значення якої не є цілочисловим, тобто

. Область

 x

простору допустимих рішень задачі лінійного програмування не

містить цілочислових значень змінної

, тому вона може бути виключена із

розгляду, як безперспективна. Це еквівалентно заміні вихідної задачі

лінійного програмування 1-3 двома новими задачами лінійного

програмування, котрі визначаються наступним чином:

а) задача 1:





















623

max4

2,1

xxz

б) задача 2:



















623

max4

2,1

xxz

Нові обмеження виключають одна одну, тому задачу 1 і задачу 2

необхідно розглядати як незалежні задачі лінійного програмування.

Оптимальне рішення задачі цілочислового програмування знаходиться або в

просторі допустимих рішень задачі 1, або задачі 2. Отже обидві звдачі

необхідно розв’язати.

Спочатку розв’яжемо задачу 1. Для цього спочатку з останньої

симплекс-таблиці задачі 1-3 змінну

виразимо через небазисні невідомі:

431

xxx





Тепер нове додаткове обмеження

x

запишемо в канонічній формі і

допишемо його до останньої симплекс-таблиці задачі 1-3:

543







xxx

Отже за допомогою двоїстого симплекс-методу можемо розв’язати задачу 1:

і Базис С

4 1 0 0 0

1 А

1 1 0 1 1/3 -1/3 0

2 А

4 8/3 1 0 2/9 1/9 0

3 А

0 -2/3 0 0 -2/9 -1/9 1

4 35/3 0 0 11/9 0 0

1 А

1 3 0 1 1 0 -3

2 А

4 2 1 0 0 0 1

3 А

0 6 0 0 2 1 -9

4 11 0 0 1 0 1

Оптимальним розв’язком задачі 1 буде

)3;2(

x

, а максимальне

значення цільової функції відповідно -

11324

max

Z

. Оптимальне рішення

задачі 1 задовольняє умову 5, тобто умову цілочисленості.

В цій ситуації ми не можемо оцінити якість рішення, отриманого при

розгляді задачі 1, оскільки розв’язок задачі 2 може привести до кращого

цілочисельного розв’язку(з більшим значенням цільової функції). Поки що

ми можемо лише сказати, що значення

max

Z

являється нижньою

границею максимального значення цільової функції вихідної задачі 1-4.

При значенні нижньої границі

max

Z

розглянемо задачу 2.

Аналогічно до задачі 1 маємо:

643









xxx

і Базис С

4 1 0 0 0

1 А

1 1 0 1 1/3 -1/3 0

2 А

4 8/3 1 0 2/9 1/9 0

3 А

0 -1/3 0 0 2/9 1/9 1

4 35/3 0 0 11/9 0 0

Оскільки для b=-1/3 в рядку, що йому відповідає немає від’ємних

чисел, то задача 2 розв’язку не має.

Отже оптимальним рішенням задачі лінійного цілочислового

програмування являється нижня границя, а саме

)3;2(

x

, при цьому

значення цільової функції

max

Z

Як бачимо, розв’язки, отримані трьома способами однакові.

VI. Вихідний код програми

Нижче приведемо код програми для знаходження мінімуму фіункції

за допомогою методу золотого перерізу і методу Фібоначчі, реалізований в

С++. Результат виконання програми виводить в окремий текстовий документ

Solution.txt.

 Метод золотого перерізу

// zoloto.cpp : Defines the entry point for the console application.

#include "stdafx.h"

#include <iostream>

#include <cmath>

#include <fstream>