Кукин Г.Н. и др. Текстильное материаловедение. Текстильные полотна и изделия
Подождите немного. Документ загружается.

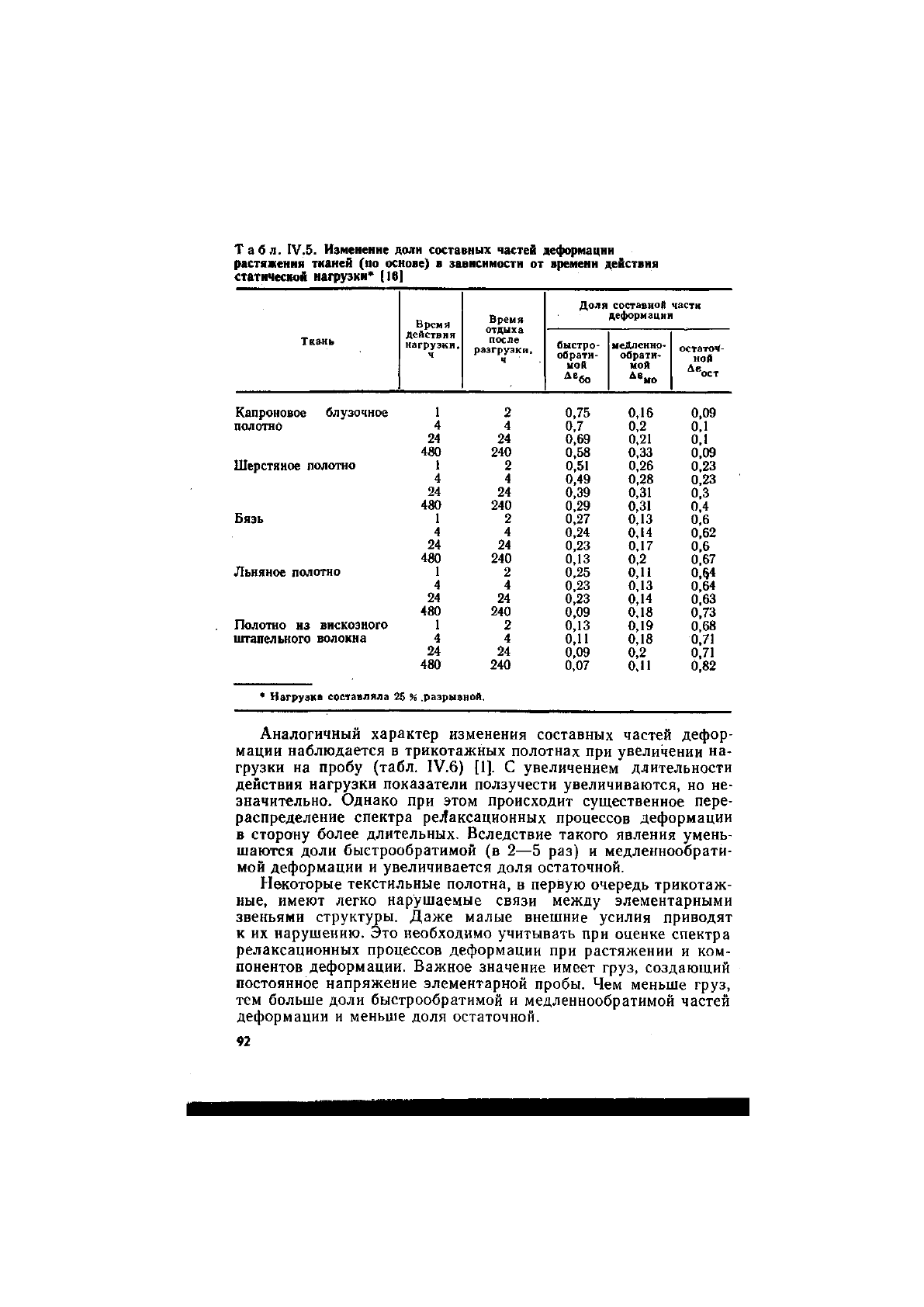
Табл. IV.5. Изменение доли составных частей деформации
растяжения тканей (по основе) в зависимости от времени действия
статической нагрузки* [16]
Ткань
Время
действия
нагрузки,
ч
Врем»
отдыха
после
разгрузки,
ч
Доля составной части
деформации
быстро-
обрати-
мой
Де
бо
меДленно-
обрати-
мой
Д8
мо
остаточ-
ной
Ае
ост
Капроновое блузочное
1
2
0,75 0,-16 0,09
полотно
4
4
0,7 0,2 0,1
24
24
0,69 0,21
0,1
480
240
0,58 0,33
0,09
Шерстяное полотно
1
2
0,51
0,26 0,23
4 4
0,49 0,28 0,23
24
24
0,39 0,31
0,3
480
240
0,29
0,31
0,4
Бязь
1
2
0,27
0,13
0,6
4 4
0,24 0,14
0,62
24 24
0,23
0,17
0,6
480
240
0,13 0,2 0,67
Льняное полотно
1
2
0,25 0,11
0,§4
4
4
0,23 0,13
0,64
24
24
0,23
0,14
0,63
480
240
0,09
0,18
0,73
Полотно из вискозного 1
2
0,13
0,19 0,68
штапельного волокна
4 4
0,11 0,18
0,71
24
24
0,09 0,2
0,71
480 240
0,07
0,11
0,82
* Нагрузка составляла 25 % .разрывной.
Аналогичный характер изменения составных частей дефор-
мации наблюдается в трикотажных полотнах при увеличении на-
грузки на пробу (табл. IV.6) [1]. С увеличением длительности
действия нагрузки показатели ползучести увеличиваются, но не-
значительно. Однако при этом происходит существенное пере-
распределение спектра реЛаксационных процессов деформации
в сторону более длительных. Вследствие такого явления умень-
шаются доли быстрообратимой (в 2—5 раз) и медленнообрати-
мой деформации и увеличивается доля остаточной.
Некоторые текстильные полотна, в первую очередь трикотаж-
ные, имеют легко нарушаемые связи между элементарными
звеньями структуры. Даже малые внешние усилия приводят
к их нарушению. Это необходимо учитывать при оценке спектра
релаксационных процессов деформации при растяжении и ком-
понентов деформации. Важное значение имеет груз, создающий
постоянное напряжение элементарной пробы. Чем меньше груз,
тем больше доли быстрообратимой и медленнообратимой частей
деформации и меньше доля остаточной.
92
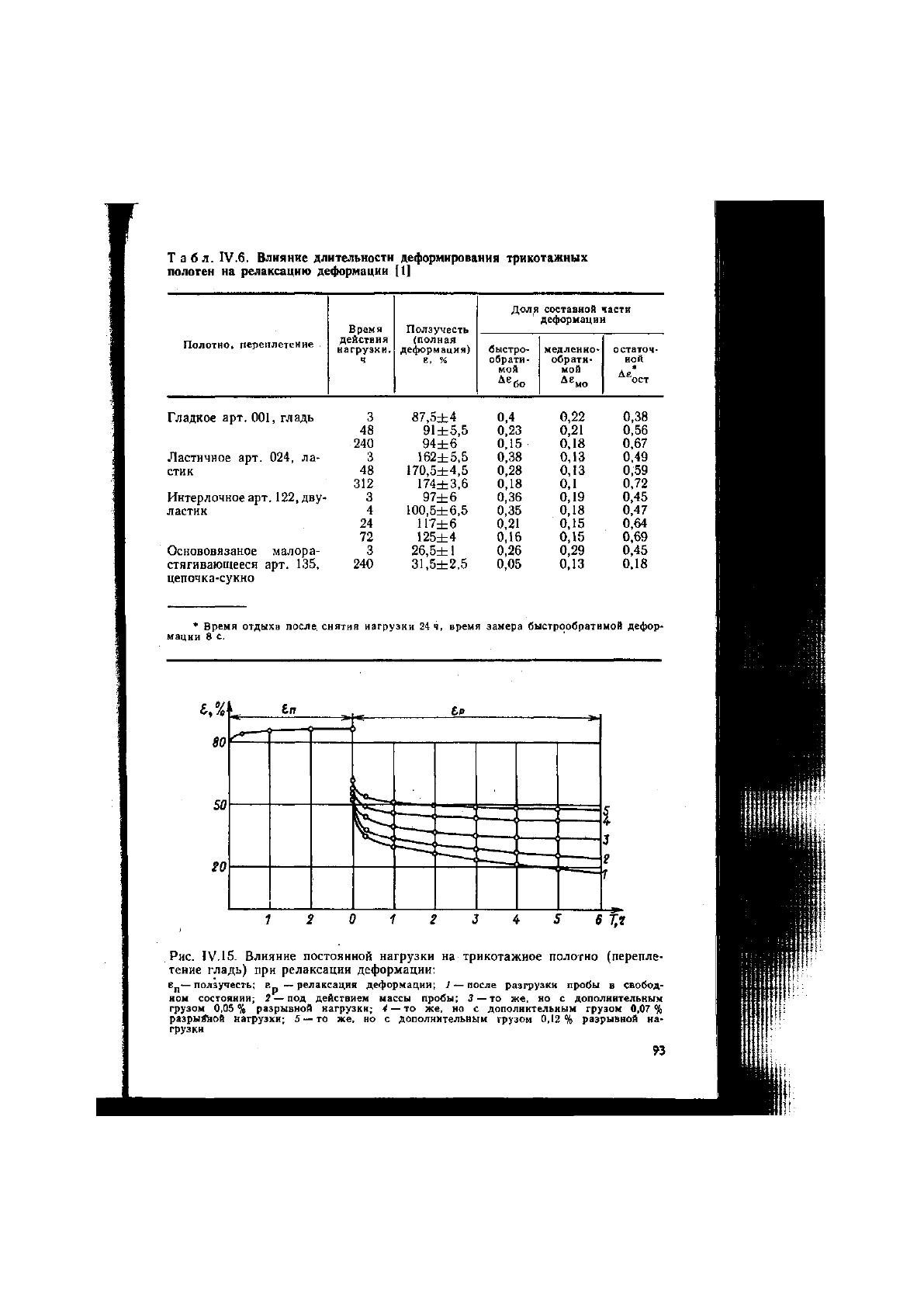
Табл. IV.6. Влияние длительности деформирования трикотажных
полотен на релаксацию деформации [1]
Полотно, переплетение
Время
действия
нагрузки,
ч
Ползучесть
(полная
деформация)
8, %
Доля составной части
деформации
быстро- медленно- остаточ-
обрати-
обрати-
ной
мой
мой
Де
ост
Де
бо
Де
мо
Де
ост
Гладкое арт. 001, гладь 3
48
240
Ластичное арт. 024, ла- 3
стик 48
312
Интерлочное арт. 122, дву- 3
ластик 4
24
72
Основовязаное малора- 3
стягивающееся арт. 135, 240
цепочка-сукно
87,5±4 0,4 0,22
0,38
91±5,5 0,23
0,21
0,56
94±6 0,15
0,18
0,67
162±5,5 0,38 0,13 0,49
170,5±4,5
0,28
0,13 0,59
174±3,6
0,18
0,1 0,72
97±6 0,36
0,19 0,45
100,5±6,5 0,35
0,18 0,47
117±6 0,21 0,15
0,64
125±4
0,16 0,15
0,69
26,5±
1
0,26 0,29 0,45
31,5±2,5
0,05
0,13 0,18
* Время отдыха после снятия нагрузки 24 ч, время замера быстрообратимой дефор-
мации 8 с.
во
so
го
In
i
—
е
—<
!
_
е
=d
6 T,t
Рис. IV.15. Влияние постоянной нагрузки на трикотажное полотно (перепле-
тение гладь) при релаксации деформации:
е
п
— ползучесть; Ер — релаксация деформации; 1 — после разгрузки пробы в свобод-
ном состоянии; 2 — под действием массы пробы: 3 — то же, но с дополнительным
грузом 0,05 % разрывной нагрузки; 4 — то же, но с дополнительным грузом 0,07 %
разрывной нагрузки; 5 — то же, но с дополнительным грузом 0,12% разрывной на-
грузки
93
Экспериментальное определение течения релаксационного про-
цесса деформации трикотажного полотна при разных грузах,
создающих постоянное напряжение элементарной пробы, под-
твердило торможение релаксационного процесса, менее замет-
ное для быстрообратимой деформации и существенное для мед-
леннообратимой и остаточной деформации (рис.
IV.
15).
Модельные методы изучения релаксации
и ползучести при растяжении
Модельные методы изучения релаксационных процессов напря-
жения и деформации текстильных полотен при растяжении по-
лучают широкое применение не только для изучения явлений,
происходящих в полотнах при растяжении, но и для прогнози-
рования поведения в различных условиях эксплуатации. При-
менительно к текстильным материалам модельные методы изу-
чения описаны в ряде монографий и учебников, применительно
к волокнам и нитям — в учебнике по текстильному материало-
ведению волокон и нитей, поэтому здесь рассматриваются пер-
спективные модели для изучения и прогнозирования механиче-
ских свойств текстильных полотен. Выбор модельных .методов
должен производиться на основе механизма растяжения поло-
тен и тех релаксационных процессов, которые в них проис-
ходят.
При растяжении текстильных полотен происходят релакса-
ционные процессы деформации, напряжения, а также ползуче-
сти. Вследствие растяжения текстильных полотен возникают
упругая, эластическая и пластическая деформации. Доля упру-
гой деформации, связанной с изменением межатомного расстоя-
ния, расстояния между частицами вещества, не может быть зна-
• Ь,%
30.
т.
1
г j
*
С
п
}
Л*
5
S4
*
—
N к
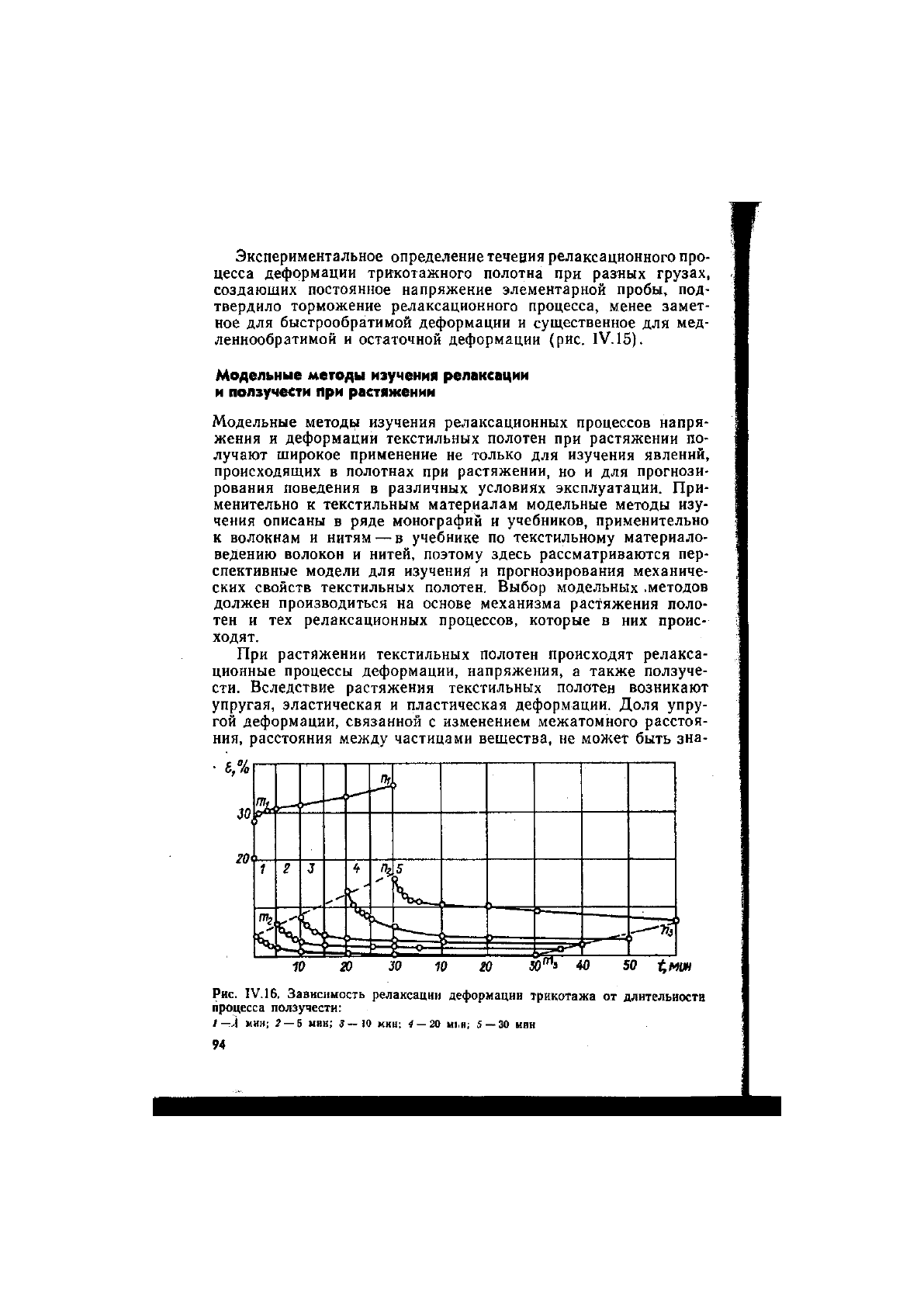
Рис. IV.
16.
Зависимость релаксации деформации трикотажа от длительности
процесса ползучести:
I—А мин; 2
— 5
мин; 3 — 10 мин; 4 — 20 мьн; 5
— 30
мин
94
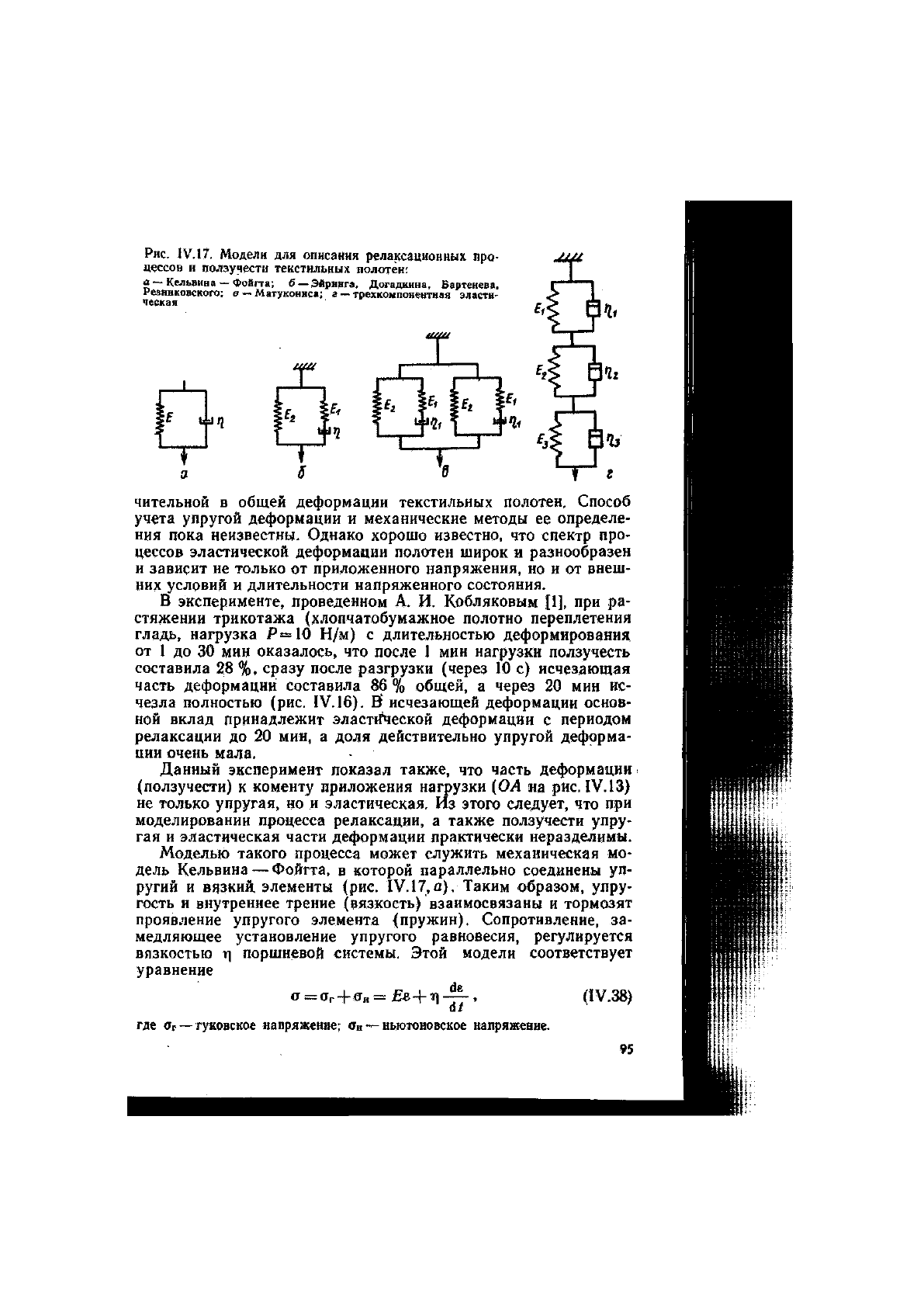
Рис. I V.I
7.
Модели для описания релаксационных про-
цессов и ползучести текстильных полотен:
а —Кельвина — Фойгта; б — Эйринга. Догадкнна, Бартенева,
Резннковского; в — Матуконнса; г — трехкомпонентиая эласти-
ческая
т
а
tAirj
Иг
111
г
чительной в общей деформации текстильных полотен. Способ
учета упругой деформации и механические методы ее определе-
ния пока неизвестны. Однако хорошо известно, что спектр про-
цессов эластической деформации полотен широк и разнообразен
и зависит не только от приложенного напряжения, но и от внеш-
них условий и длительности напряженного состояния.
В эксперименте, проведенном А. И. Кобляковым {!], при ра-
стяжении трикотажа (хлопчатобумажное полотно переплетения
гладь, нагрузка Р—10 Н/м) с длительностью деформирования
от 1 до 30 мин оказалось, что после 1 мин нагрузки ползучесть
составила 28%, сразу после разгрузки (через 10 с) исчезающая
часть деформаций составила 86 % общей, а через 20 мин ис-
чезла полностью (рис.
IV. 16) .
В' исчезающей деформации основ-
ной вклад принадлежит эластической деформации с периодом
релаксации до 20 мин, а доля действительно упругой деформа-
ции очень мала.
Данный эксперимент показал также, что часть деформации
(ползучести) к коменту приложения нагрузки (OA на рис.
IV.
13)
не только упругая, но и эластическая. Из этого следует, что при
моделировании процесса релаксации, а также ползучести упру-
гая и эластическая части деформации практически неразделимы.
Моделью такого процесса может служить механическая мо-
дель Кельвина — Фойгта, в которой параллельно соединены уп-
ругий и вязкий, элементы (рис. IV. 17,а). Таким образом, упру-
гость и внутреннее трение (вязкость) взаимосвязаны и тормозят
проявление упругого элемента (пружин). Сопротивление, за-
медляющее установление упругого равновесия, регулируется
вязкостью т] поршневой системы. Этой модели соответствует
уравнение
а =
<т
г
-f о
и
= Ег
-f-
ц ,
at
где а
г
— гуковское напряжение; а
и
— ньютоновское напряжение.
95

В интегральной форме уравнение ползучести согласно этой
модели при о=const имеет вид
е
= -|-(1— exp—tlx),
или
е =
е
0
(1
—ехр—</т); (IV.39)
уравнение релаксации деформации описывается уравнением
е = е
0
ехр—//0, (IV.40)
где ео — величина деформации пробы (показатель ползучести) к моменту сня-
тия внешних усилий; т и 8 — константы, характеризующие длительность про-
цесса ползучести и релаксации деформации.
Численно т показывает, за какой интервал времени ползу-
честь достигает (е—1)/е-й доли предельного значения, а 9 —
время, за которое полная деформация уменьшается в е раз.
Один блок модели не отражает реального положения при
релаксации деформации, а также при ползучести.
В модели Эйринга, Догадкина, Бартенева, Резниковского [1,
4, 17] по сравнению с моделью . КельвинаФойгта в ветвь
с внутренним трением подключается дополнительная пружина
(рис. IV. 17,б), т. е. добавляется упругий элемент, чем усилива-
ется упругая составляющая часть. Эту модель часто используют
также при исследовании релаксационных явлений в волокнах
и нитях.
Уравнение релаксации напряжений для этой модели имеет
вид
^ (q
— Qoo)
_ jg de а
— goo
At ~ At x
где a=Eeo — общее напряжение системы; cr,» =Е<х,Во — установившееся рав-
новесное напряжение; ео — деформация системы; e=eo=const.
А. В. Матуконис [18], стремясь приблизить модель к реаль-
ным условиям релаксационных процессов с различными перио-
дами релаксации, объединяет две модели в одну (рис. IV.17,в).
Учитывая практические данные о -течении релаксационных
процессов деформации, когда резко выделяются процессы с ма-
лым периодом релаксации, с достаточно большим периодом ре-
лаксации эластической и пластической деформаций, Г. Н. Кукин
и А. Н. Соловьев [6] предложили трехкомпонентную эластиче-
скую модель, которая выражается формулой
е = е
у
ехр~АТ
1
+ е
э
ехр — В
1
Т
2
, (IV.41)
где е
у
— упругая деформация; А и Bi — коэффициенты на поправку, учиты-
вающие отклонение экспериментальных величин упругой и эластической де-
формаций от реальных величин; Тi — время нагрузки; е
а
— эластическая
деформация: Т
г
— время отдыха после разгрузки.
96

А. И. Кобляковым было установлено, что при нагрузках, не
превышающих 10 % разрывной, пластическая часть деформации
практически отсутствует, поэтому можно допустить для трико-
тажных полотен трехкомпонентную эластическую модель
(рис.
IV.
17,г), где 1-е звено отражает быстрообратимую, или на-
чальную, деформацию с временем до 5 с, 2-е звено — замедлен-
ную с временем релаксации до 2—4 ч, а 3-е звено — затормо-
женную эластическую деформацию с временем релаксации до
десятков и сотен часов, но в условиях, ускоряющих процесс ре-
лаксации. Эта часть деформации также исчезает.
В общем виде уравнение трехкомпонентной обобщенной ме-
ханической модели с эластическим механизмом имеет вид
т t
—j е-«~
0
>/
г
а (т) dr. (IV.42)
(=i
11
о
Конкретно для трехкомпонентной модели деформация
в = Eje-'/
0
. -f е
2
е-'/
0
» +
е
3
е~</
0
»,
(I V.43)
где ei, е
2
, е
3
— деформации, исчезающие со средним временем запаздывания
6t, 0г, в
3
.
Уравнение релаксации напряжения для этого процесса имеет
вид
a = а
х
е-'/
т
' + <т
2
е
_,/х
> -f а
3
е
-</т
», (IV.44)
где 01, Ог, о
3
— напряжения, уменьшающиеся со средним временем релакса-
ции Ti, т
2
, т
3
.
По этой же модели можно рассчитать ползучесть. При по-
стоянном напряжении ползучесть
е =
(1 _
е
</Ф.) + SL (1 __е-'/*») + (1 _е-V*), (IV.45)
Ei
или
е = а
х
(1
—е-'/".) + a
2
(1
—ег</*) + а
3
(1
— е-</<*). (IV.45a)
где а 1, а
2
, аз — деформации со средним временем ползучести q>i, «рг, фз.
Приведенные уравнения соответствуют непрерывному про-
цессу. В действительности релаксационный процесс представляет
собой отдельные перемещения. Дискретные перемещения, как
показано А. И. Коблякбвым [1], могут быть значительными, но
в подавляющем большинстве случаев периоды между переме-
щениями очень малы, особенно в начальной стадии релаксации.
Поэтому вполне допустимо принять процесс релаксации"тек-
стильных полотен как непрерывный процесс.
Расчет параметров механической модели релаксации дефор-
мации. Постоянные уравнения релаксации как деформации, так
4 Заказ Nk 1031 97

и напряжения можно определить графоаналитическим способом.
Уравнение (IV.43) преобразуется к виду
где
е = е^-"»'
-f-
е
4
е-
а
«' -f egr
0
**,
(IV.46)
«1=1/вх; (IV.47a)
а
2
= 1/0
2
; (IV.476)
а
3
= 1/0
8
. (IV.47BJ
Первое граничное условие модели:
при /,=0 е = е
1
+ е
2
+
е
3
= е
0
,
где ео — деформация пробы перёд релаксацией, или полная деформация.
Второе граничное условие модели:
при t-*-aо е» = + е
а
+ е
3
= 0.
Расчет параметров модели выполняется в определенной по-
следовательности.
1. Определяют параметры 8з, а
3
, 0з. Для этого из равенства
(IV.46) исключаются компоненты, характеризующие быстро и
медленно протекающие процессы.
е
исч
= е
1
е
-
«•' + е
2
е- .
Тогда релаксационный процесс заторможенной эластической
деформации можно представить выражением
е = е
3
е-<4 (IV.48)
Логарифмируя равенство, получаем уравнение
lge = lge
8
-a
s
flge, (IV.49)
которое является уравнением прямой
у
г
=а + Ьх,
где
a = lge
8
; (IV.50)
6 = 0,4343a
3
. (IV.51)
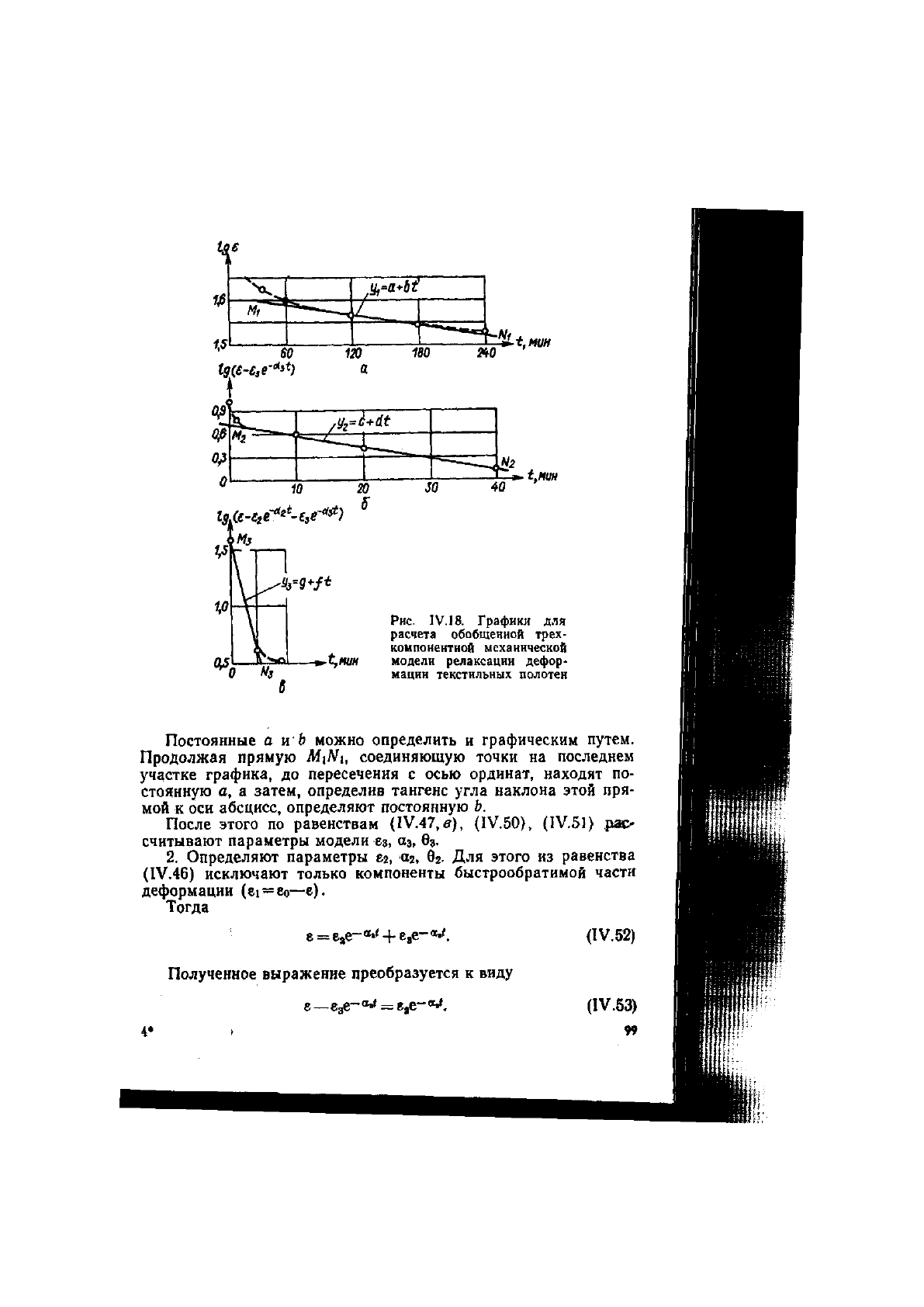
По значениям lge и t строится график (рис.
IV.
18,а), на ко-
тором имеется участок прямой MiAfi, совпадающий полностью
или наибольшим числом точек с экспериментальной кривой. Этот
участок характеризует течение очень медленных процессов ре-
лаксации деформации. Аналитическим путем, используя метод
наименьших квадратов, рассчитывают постоянные а и b урав-
нения прямой AfjAV.
a=
S<*Sщ-zmyt .
nSt*— (2/)» '
b==
nZtyi-StSAyi
W
ш
V
V,
^a+bt
Ml
Г
JfMj
-Nj
t,MUH
t,HUH
Рис.
IV. 18.
Графики для
расчета обобщенной трех-
компонентной механической
модели релаксации дефор-
мации текстильных полотен
Постоянные а и b можно определить и графическим путем.
Продолжая прямую MiNi, соединяющую точки на последнем
участке графика, до пересечения с осью ординат, находят по-
стоянную а, а затем, определив тангенс угла наклона этой пря-
мой к оси абсцисс, определяют постоянную Ь.
После этого по равенствам (IV.47,в), (IV.50), (IV.51) рм>
считывают параметры модели ез, а
3
, в
3
.
2. Определяют параметры ег, «2, бг- Для этого из равенства
(IV.46) исключают только компоненты быстрообратимой части
деформации (ei=e
0
—е).
Тогда
е = в
а
е
_
а
»<
+ е
8
е~ <*•'. (IV.52)
Полученное выражение преобразуется к виду
е—взв
-
= (IV .53)
4* * W

Обозначив е—езе-^'^е' и прологарифмировав выражение
.(IV.53), получают уравнение прямой
Ige' = lge
a
-(a
a
lge)/ (IV .54)
или
y>r=c+dt, (IV.55)
где
c = lge
a
; (IV. 56)
d=—0,4343а
а
. (IV.57)
Аналогично предыдущему по значениям Ige' и t строят гра-
фик (рис. IV. 18,б), на котором отмечают участок прямой M
2
N
2
,
характеризующий течение замедленных процессов деформации.
Рассчитывают постоянные cud уравнения прямой M
2
N
2
:
nSP-fSO* '
v
'
nS<»-(S<)
a
Определив постоянные с и d по равенствам (IV.56), (IV.57),
рассчитывают параметры г
2
, а
2
, 02.
3. Определяют параметры ei, а
ь
0j. Для этого уравнение
(IV.46) преобразуют к виду
е—е
а
е~ "Л—е
3
е
— а
»'
—
е^-ом», (IV.60)
Обозначив е'—е
2
е~
а
»
(
— е."
и е'=е—е
3
е-
а
«* и подставив
в выражение (IV.60), получают
г" = 8ie
_a
>'. (IV, 61)
Логарифмируя обе части равенства
lge"-lge
1
~(a
1
-lgeH, (IV.62)
получают уравнение прямой
y
3
=g + ft, (IV.63)
где
$ = lgei. (IV. 64)
/=— 0,4343«i. (IV.65)
По значениям lge" и t строят график, на котором отмечают
отрезок прямой M
3
N
3
(рис. IV.18,в), характеризующий течение
ускоренных процессов релаксации. Рассчитывают постоянные
8
'
(IV
-
66)
/ва
n*ty,-za
¥
,
v
' nZt* -(SO
8
100

После этого по формулам (IV.64), (IV.65) и (IV.47a) опреде-
ляют параметры ei, ai, 61.
Расчет параметров модели релаксации напряжения принци-
пиально не отличается от расчета параметров модели релакса-
ции деформации (IV.45). В алгоритме заменяют е; на о; и а<
на
Р
г
= 1/т
г
; р
3
=1/т
3
.
Расчет параметров модели ползучести деформации. Для рас-
чета ползучести текстильных полотен можно использовать спо-
соб, примененный Ф. Винклером [19] для расчета ползучести ни-
тей. В уравнении
е = д,
(1
—е- w.) + а
2
(1
-е-'/
0
») + а
3
(1
—е-'/
0
»)
принимают
bi-еГ
1
; (IV.68)
Ь
г
= ЬТ\ (IV.69)
b
s
= вГ'; (IV.70)
Oo^ai +
ец
+ аз.
Тогда уравнение преобразуют к виду
е = а
0
—aje-W—а
2
е-^'—а
3
е-"Ч (IV.71)
где ао — ползучесть при <->-00; Oi — начальная ползучесть; а
2
— ползучесть
на второй замедляющейся фазе; а
3
— ползучесть при очень медленных про-
цессах.
Параметры модели рассчитывают последовательно.
1. Определяют параметры а
3
, Ьз, т
3
. Ползучесть при очень
медленных процессах Выражают равенством
азе-М = а
0
-е, (IV.72)
где е=е(/) — деформация в текущих координатах.
Величину ао выбирают произвольно, но обязательно больше
максимально замеренной величины деформации е. Например,
для хлопчатобумажного трикотажного полотна при растяжении
по ширине нагрузкой 5 % разрывной при максимальной дефор-
мации
е
= е( 180) =87,5 % о
0
=88,5%.
Логарифмируя обе части равенства (IV.72), получают
lg(ao-e) = lga
3
-0,4343M.
Заменяя
(IV.73)
lga
a
= a; (IV.74)
—0,4343b
3
= 6, (IV. 75)
получают уравнение прямой
y
1
= a + bt. (IV. 76)
101
